一种改进的DV-Hop定位算法

胡玉兰,于 溪,赵青杉

(忻州师范学院，山西 忻州 034000)

0 引言

无线传感器网络(Wireless Sensor Network,WSN)是指由大量的传感器构成的分布式传感器网络.由于其具有低功耗、体积小、价格低等优点进而被广泛利用.因此WSN在监测网络部署区域发挥着重要的作用，其中的DV-Hop定位机制也广受欢迎，人们针对其存在的缺陷与不足在各种方向进行改进完善，此文即针对其中一种改进的算法进行的研究.

1 研究背景及现状

节点定位在无线传感网络中起着至关重要的作用.由于无需测距定位技术的低成本优势，许多学者致力于改进其算法进而在低成本的前提下减小定位误差：刘珍等人针对细菌觅食优化算法的缺陷提出了基于非线性递减的余弦自适应步长，并改进细菌位置的更新方式、优胜略汰的选择标准和迁徙方式对原算法进行优化[1].刘文远等人针对DV-Hop节点定位算法的缺陷引入权重及有选择的使用锚节点估计位置，进而减小误差[2].范海红等人都是通过加权重增强DV-Hop定位算法的准确率[3].张中芳等人提出了利用量子粒子群优化算法对DV-Hop节点定位算法进行优化求解提高定位精度[4].童宇行等人是采用限制跳数的方法，将已经定位的未知节点变为信标节点继续辅助定位[5].夏少波等人是采用节点密度区域划分的方法，依据网络的连通度和节点密度限制参与估算的信标节点的跳数[6].景路路等人是利用不同的信标节点,计算出不同的平均跳距,使它更接近于实际的平均每跳距离[7].针对通过跳距优化后的定位算法定位误差的积累造成定位精度下降的问题，提出了一种跳距优化的改进型DV-Hop定位算法，引入跳数细化的方法，来减小计算跳距时产生的误差，进而细化平均每跳距离，使得未知节点定位误差率减小，最后利用最小二乘法求位置节点坐标.

2 DV-Hop节点定位算法

2.1 无线网络技术

无线传感技术在通信、信息交流等方面给我们带来了不可忽视的便利，近些年来，各类无线传感技术层出不穷，尤其是利用无线传感而发展起来的节点定位技术.现有的节点定位算法可分为两类[8]：一类是需要测量距离的算法，目前这类测距技术主要包括有TOA ( Timeof Arrival) 、RSSI (Received Signal Strength Indicator) ，AOA ( Angleof Arrival )和TDOA ( Time Difference on Arrival) 等，虽然此类技术能够更加精确的定位，但网络中的节点需要增加作为测距的硬件，增加了成本；另一类是无需测量距离的节点定位算法，其中包括有、质心算法( CentroidAlgorithm)，DV-Hop( DistanceVector-Hop) 算法等，此类型算法不仅有效降低成本、而且效率高、受环境因素影响较小，虽然定位误差率稍高，但其在可接受范围内，是可以满足大部分需求的，因此投入使用非常广泛.

2.2 传统DV-Hop节点定位算法

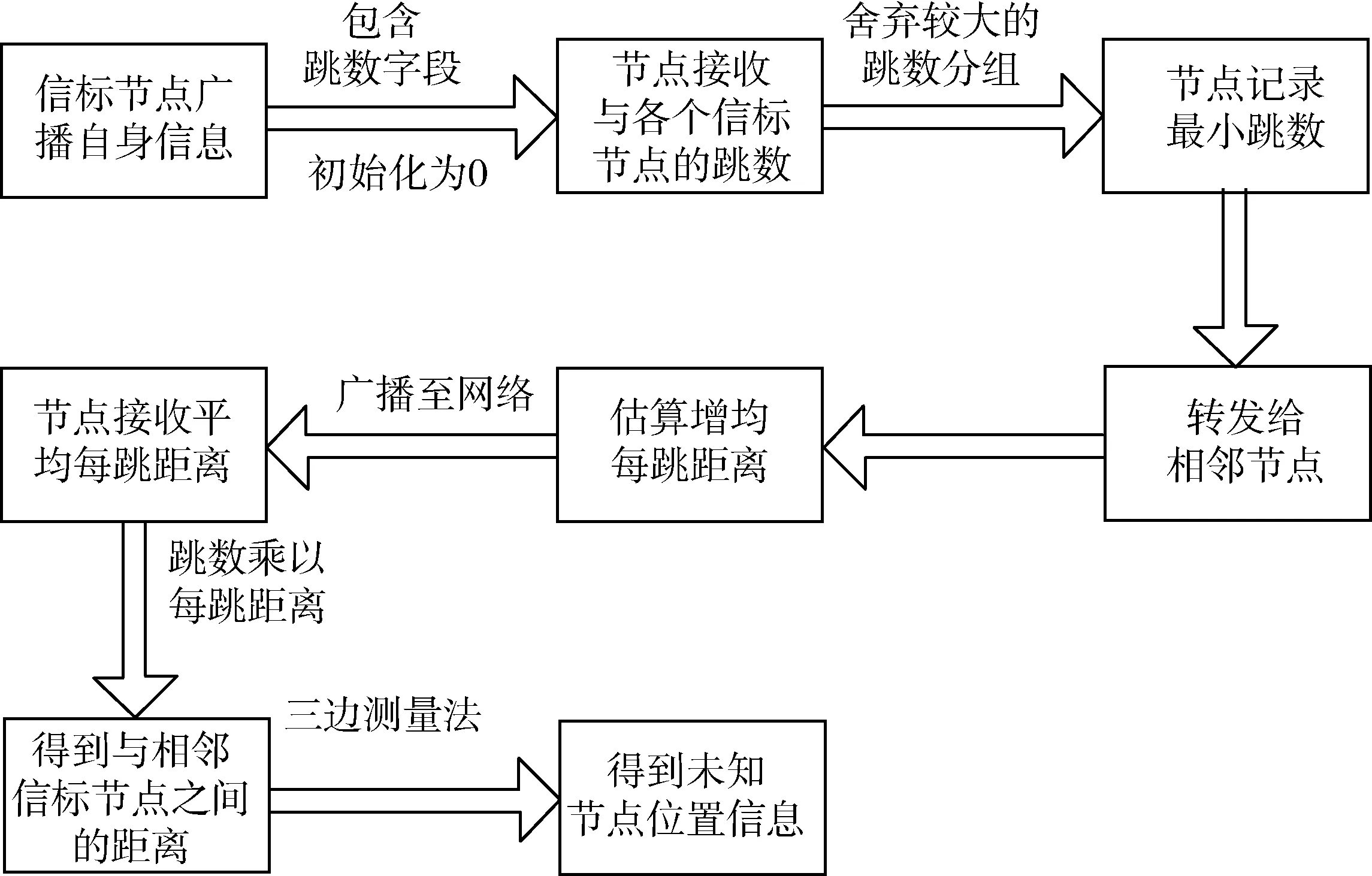
图1 传统算法实现的流程

DV-Hop定位算法是一种应用非常广泛的定位方法，它是由美国路特格斯大学的Dragos Niculescu等人提出的一种不需要测量距离的定位机制，它是利用多个知道位置信息的信标节点来实现未知节点的定位，其定位的覆盖面积较广[9，10].

传统DV-Hop定位算法的基本流程：

其中估算平均每跳距离部分，在已知两个相邻信标节点之间的距离以及两者之间的最小跳数，可利用式(1) 估算平均每跳距离，其中，(xi，yi)，(xj，yj)是信标节点i、j的坐标，hj是信标节点i与j(i≠j)之间的跳段数.

利用式(2)则可计算未知节点与信标结点之间的距离.

(1)

di=hi×HopSizeij(i≠j).

(2)

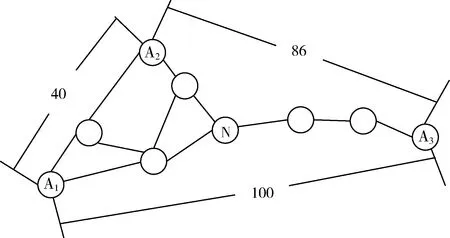
图2 传统DV-Hop算法拓扑图

下面是实际的举例：

如图2所示的拓扑图，其中A1,A2,A3是信标节点，N为欲求位置信息的未知节点，假设未知节点N从A2获得校正值.采用上述公式，可以得到信标节点A2的平均跳距为:

( 40 +86) / ( 2+ 5) = 18.

(3)

它与节点A1，A2，A3之间的距离分别为：54，36，54.

最后可利用三边测量法确定节点N的位置.

DV-Hop算法不需要测量距离也不需未知节点知道自身位置信息，对节点的配置要求不高，可以减小开支，且结构简单，易于实现.其缺点是估计的距离要大于实际距离，并且其受节点密度、信标节点密度影响较大，误差率不稳定.

3 改进的DV-Hop节点定位算法

3.1 基本思想

通过对传统DV-Hop节点定位算法的分析可知，平均每跳距离的估算误差严重影响了节点定位的准确率，因此细化跳数显得尤为重要.本次改进通过细化通信半径实现，分为3次实验，R指的是未知节点与信标节点都使用的通信半径.

第一次实验新增的0.5R为信标节点专用通信半径.将信标节点的信息发送面积分为两种,即将所有节点分为两种，如图3所示，将两个部分分别命名为A，B.由于A区域是最小区域，所以A区域内的节点能接收到信标节点传递距离在R内的信息，而B区域的节点则只能接收到信标节点传递距离大于0.5R的信息.

因此最小跳数从原来的1跳降低到了0.5跳，降低了原来因跳数的判断产生的误差.节点在收到信标节点发来的信息后，再以R为半径将此信息继续传播出去.最终，每个节点都获得了到达信标节点的最小跳数.

第二次实验将信标节点的信息发送面积分为四种,即将所有节点分为四种，如图3.2所示，将两个部分分别命名为A、B、C、D.最小跳数变为0.25跳.

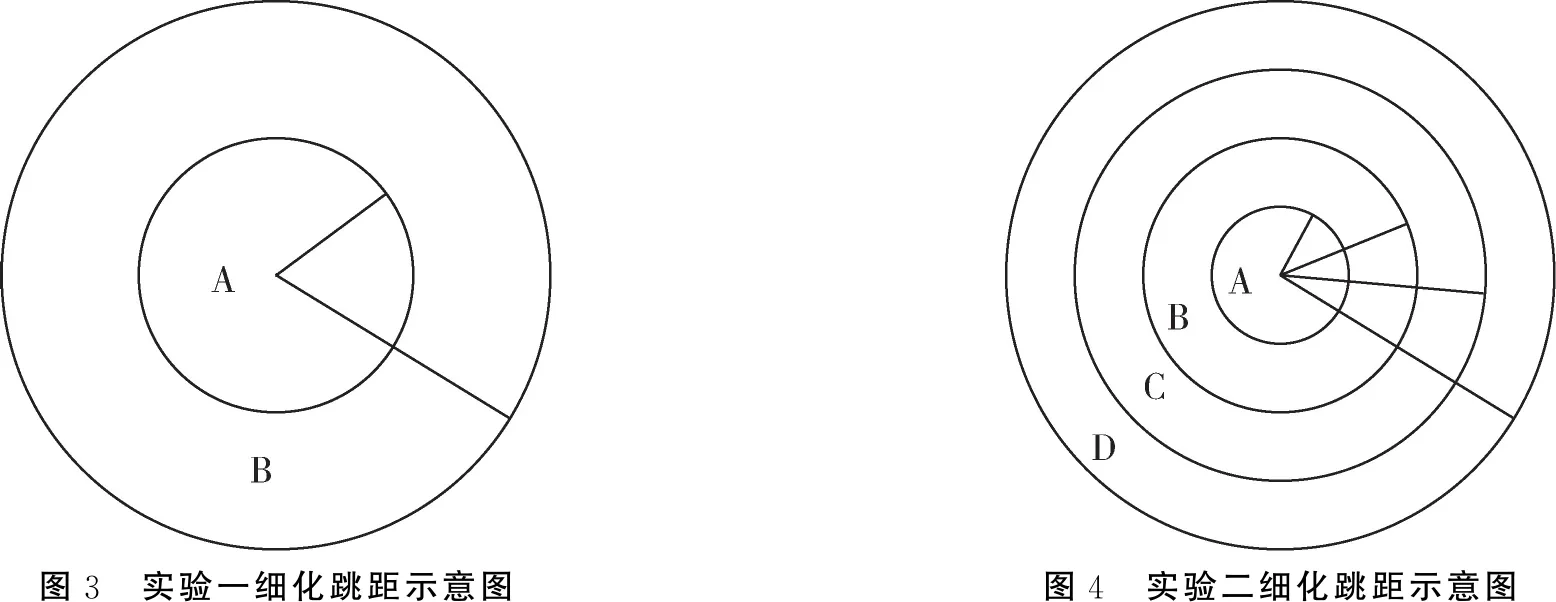
图3 实验一细化跳距示意图图4 实验二细化跳距示意图

第三次实验将信标节点的信息发送面积分为5种,即将所有节点分为5种，如图4所示，将两个部分分别命名为A，B，C，D，E.最小跳数变为0.2跳.

下面通过实例来分析：

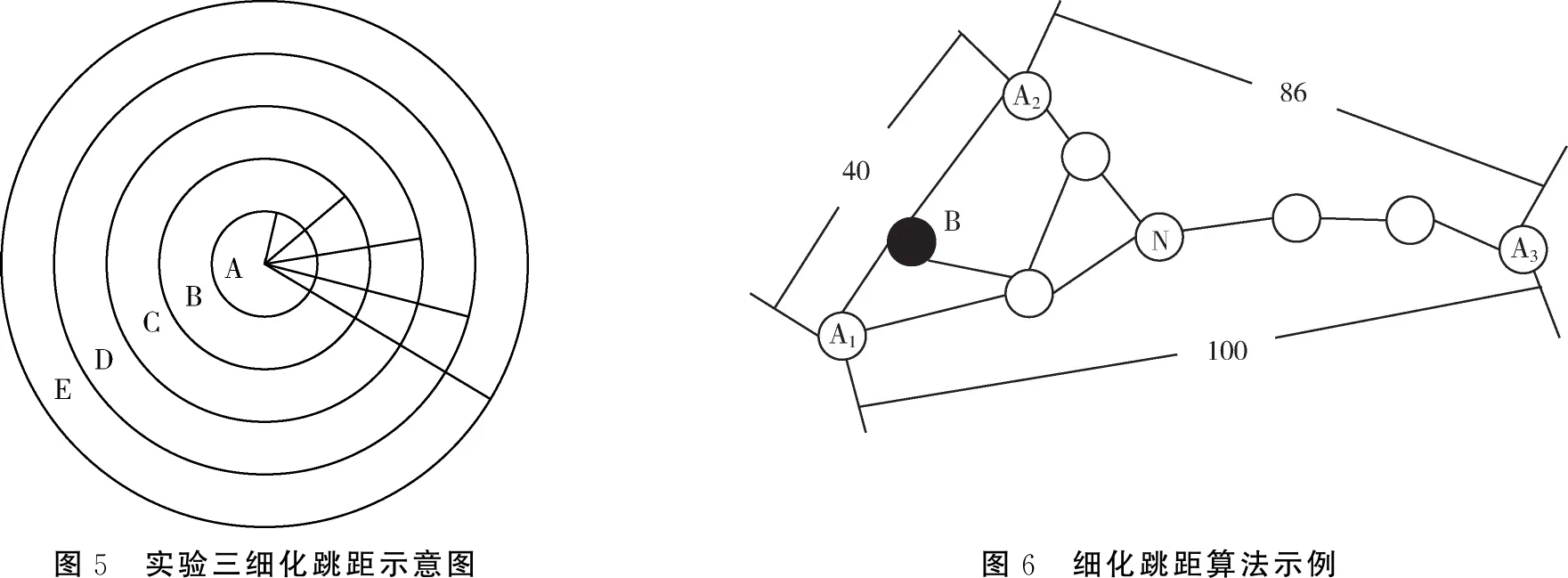
图5 实验三细化跳距示意图图6 细化跳距算法示例

以实验三为例，图6与图2作对比：A1与A2之间的跳数原来为2，经过细化之后可分为0.4和1相加得1.4.A2与N之间的跳数原来为2，经过细化之后可分为0.2和0.4相加得0.6.N与A3之间的跳数原来为3，经过细化之后可分为0.8，0.6和0.6相加得2.

(4)

式(4)比式(3)更接近与真实值.

3.2 详细步骤

以实验三为例：

第一步：获取最小跳数

1)网络初始化，信标节点第一次向外传递发送自己的分组信息.当信标节点的信息传播距离在0.2R以内时，接收到信息的节点将最小跳数记为0.2.为了降低信息传播的费用支出，此时相邻节点暂且不继续信息的转发.

2)信标节点第二次向外传递发送自己的信息分组.信标节点的信息传播距离在0.2R到0.4R之间，此时最小跳数的选择同传统的DV-Hop算法相同：若节点第一次收到信标节点的分组信息，则最小跳数为0.4；若节点在此之前已经收到过之前的信息分组，则舍弃较大的跳数值，因此最小跳数为之前的0.2.

3)信标节点第三次、四、五次向外传递信息并获得最小跳数原理同上.

第二步：估算平均每跳距离

经过第一步的节点之间的信息传送，可以得到相邻信标节点之间的最小跳数，已知信标节点的坐标，可以利用勾股定理求得两个信标节点之间的实际距离，最后利用上述式(1)计算可得平均每跳距离.

第三步：求得未知节点坐标

经过前两步的计算可以得到未知节点与信标节点之间的最小跳数与平均每跳距离，利用上述式(2)的最小跳数乘以平均每跳距离可以求得未知节点距信标节点的距离，最后利用最小二乘法求未知节点坐标.

实验一、二同上述步骤.

4 仿真结果分析

4.1 仿真实验环境

MATLAB中假设仿真环境为边长100 m的正方形区域.

4.2 仿真实验部署

4.2.1 随锚节点数目和节点变化的定位误差率

在100*100的正方形区域随机分布节点，分别在锚节点数目逐渐增加以及在节点数目逐渐增加的情况下平均定位误差，相同比例的锚节点和节点情况下，对比传统DV-Hop节点定位算法，实验进行了10次，并将10次实验结果统计到一起便于分析.并增加跳距细化程度，更改代码，重新运行，观察结果.

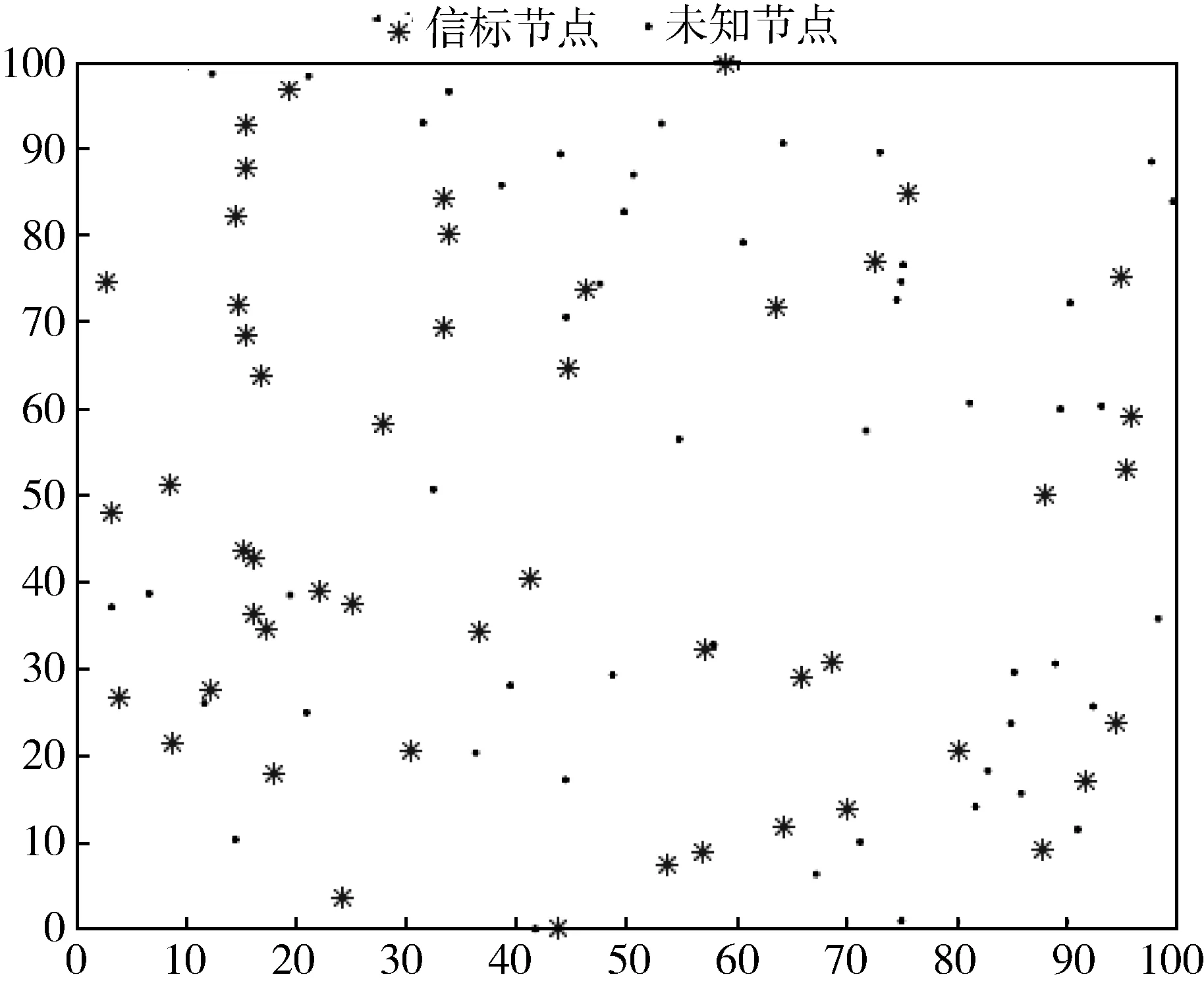
图7 仿真节点分布图

4.3 仿真实验结果图

本次实验的全部节点均为随机分布，下图7即为其中一次的节点分布图.

4.4 仿真实验分析

由于节点是每次实验随机分布的，因此只能通过传统算法与改进算法定位误差的大致差值来判断减小误差的量.

通过图8、图9、图10可以看出相比于传统算法，改进后的算法信息传播距离细化程度越大，在锚节点数大于10后，随锚节点变化的节点定位误差减小的越多.

通过图11、图12、图13可以看出相比于传统算法，改进后的算法信息传播距离细化程度越大，随节点变化的节点定位误差减小的越多.

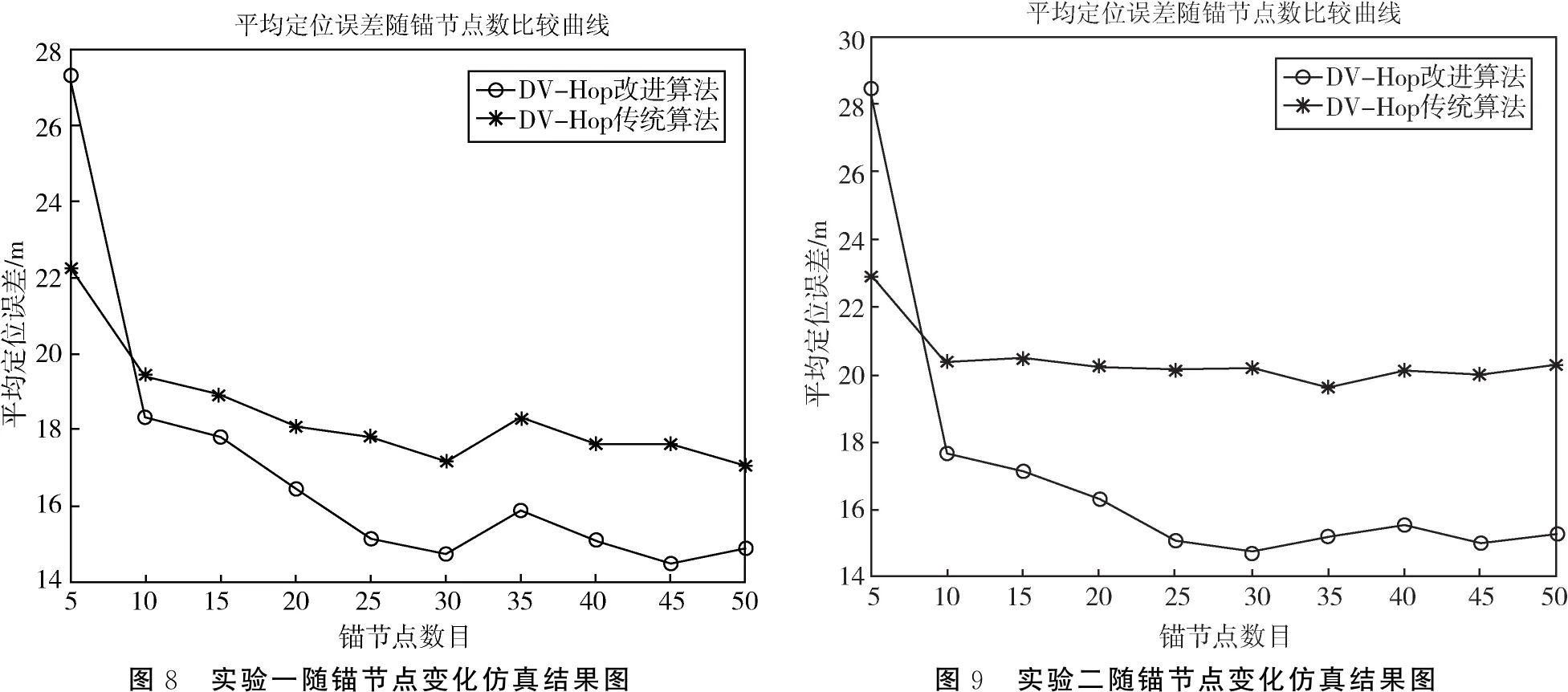
图8 实验一随锚节点变化仿真结果图图9 实验二随锚节点变化仿真结果图

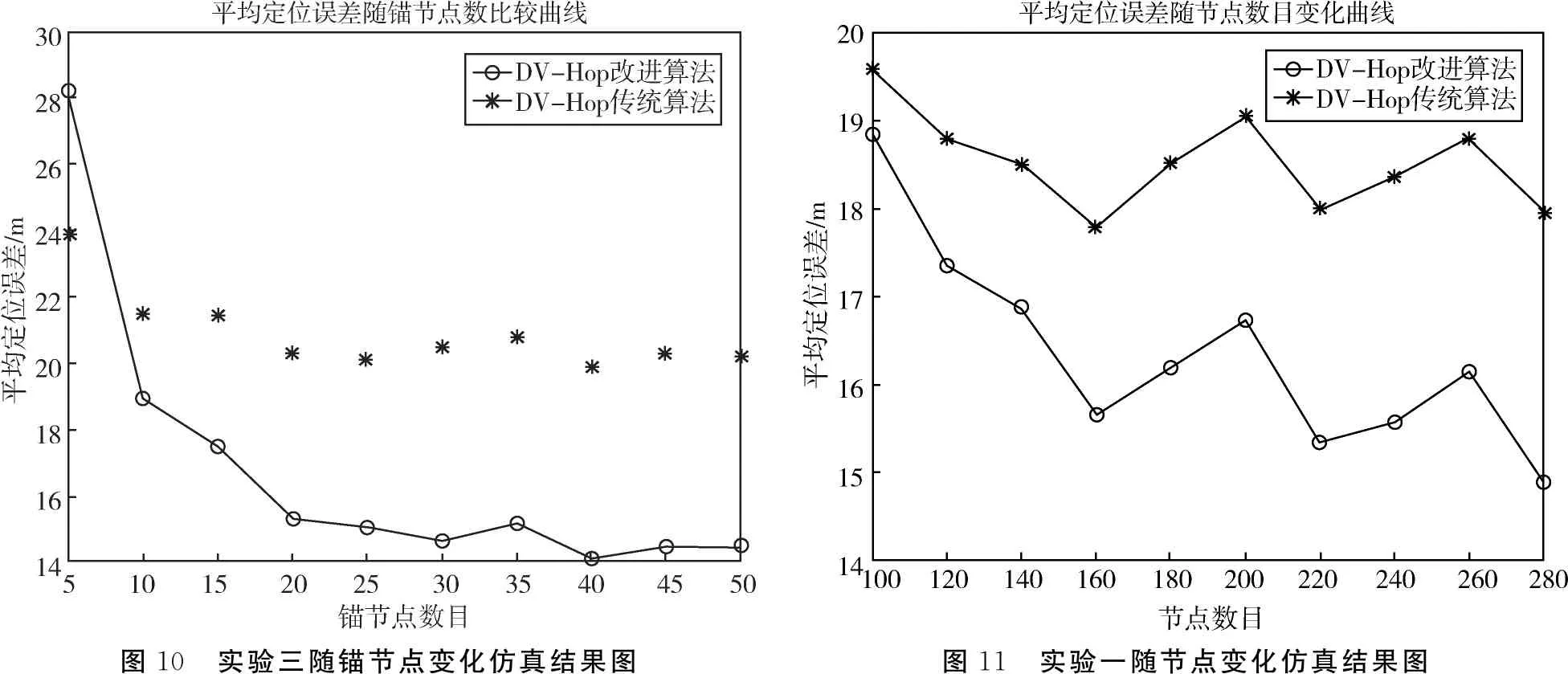
图10 实验三随锚节点变化仿真结果图图11 实验一随节点变化仿真结果图

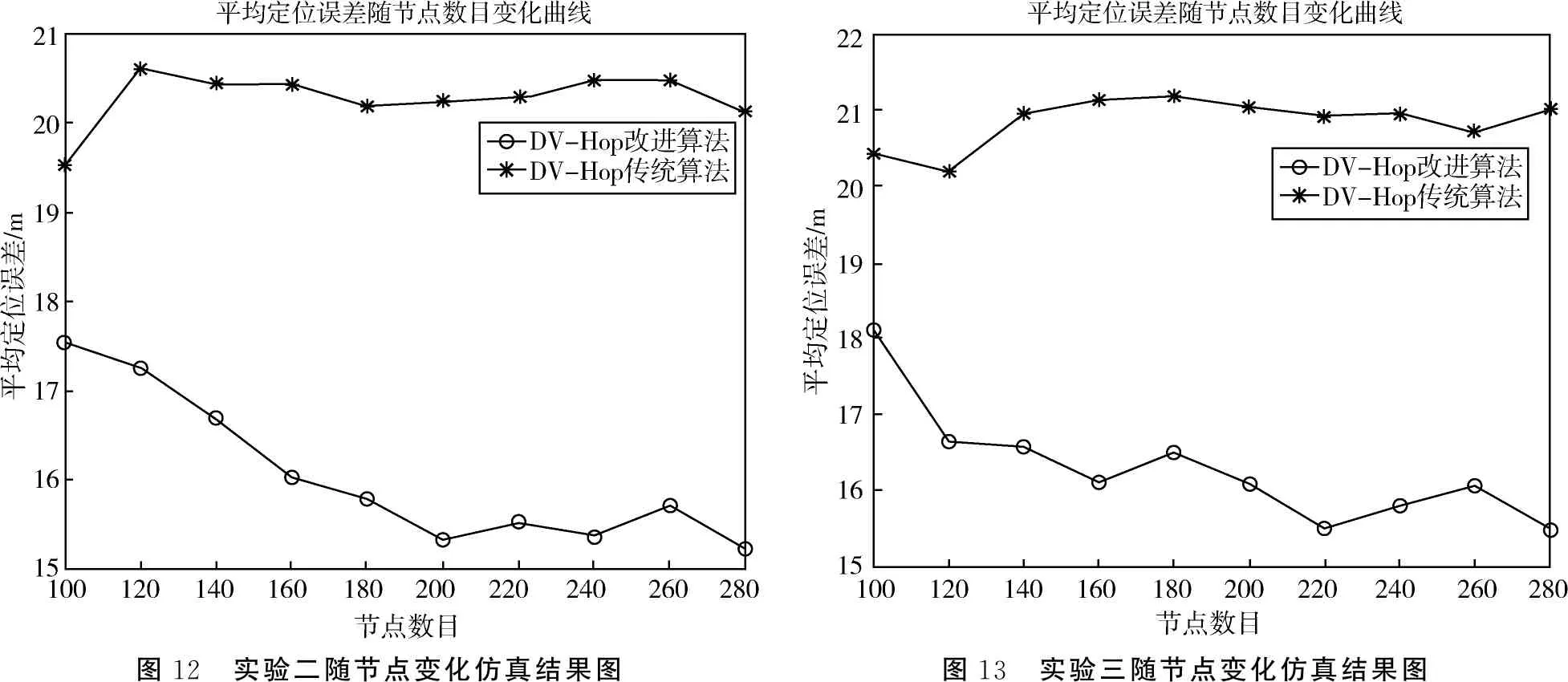
图12 实验二随节点变化仿真结果图图13 实验三随节点变化仿真结果图

5 结束语

本文首先对无线网络技术做了分析概述，并详细介绍传统的DV-Hop节点定位算法，分析其优缺点，明确误差的来源.在此基础上引入一种改进的DV-Hop算法，此算法利用细化跳距的方式减小误差，并由此算法提出进一步的改进想法：细化程度越高，误差率越低.针对此想法在Matlab上分别针对信标节点变化、节点变化进行了两种仿真实验，并通过实验进一步证明了在锚节点数足够大的情况下细化程度越高，误差率越低.

在本次实验中，也遇到了许多困难，首先是对Matlab语言的不熟悉，导致对代码的改进不顺利，以后会更加精进对语言的学习.其次本文都是在相同条件下进行10次实验，尽可能减小拓扑结构的影响，通信半径也会影响定位误差率，未来会进一步改进.