循环矩阵填充的快速傅里叶变换算法
孙青青,王川龙
(太原师范学院 数学系,山西 晋中 030619)
0 引言
近几年,矩阵填充问题是一个引人注目的新研究领域,它主要应用在模型降阶[1],机器学习[2,3],模式识别[4],控制[5]和图像恢复[6]等领域.矩阵填充问题首次由Cand`es和Recht[7]提出并通过求解如下凸优化问题:
min ‖X‖*
(1)
s.t.Xij=Mij(i,j)∈Ω
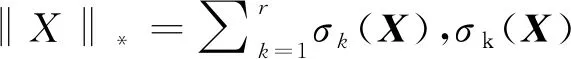
矩阵填充问题是从采样矩阵的部分已知元素合理精确地填充一个低秩矩阵.著名的Netflix推荐系统[8]就是关于矩阵填充问题的一个典型应用.因此求解优化模型(1)成为众多学者的研究热点,目前已有大量的算法被提出来解决问题(1).Fazel[9,10]首先提出了半正定规划的内点算法,但此算法不适合求解大型矩阵的填充问题.Toh和 Yun[11]提出了迭代复杂度为的加速的近端梯度法(APG).Ma和Goldfard[12]将近似奇异值分解技术应用到不动点延续算法(FPC),提出了FPCA算法,完善并改进了FPC算法.几乎同时,Cai等人[13]提出了奇异值阈值算法(SVT),该算法保持了填充矩阵的稀疏性,可以有效地处理大规模矩阵填充问题.随后,Lin等人[14]提出了阈值的增广Lagrange乘子算法(ALM),并经过一系列数值实验证明ALM算法比SVT算法和APG算法收敛速度快.另外,一些其他学者还研究了无奇异值分解的快速奇异值阈值法(FastSVT[15]),加速奇异值阈值法(ASVT[16]),梯度投影算法[17],图像修复中截断P范数正则化[18]等方法来解决矩阵填充问题.
在实际应用过程中,采样矩阵往往具有形如循环,Toeplitz,Hankel和Toeplitz-plus-Hankel等特殊结构,因此研究特殊矩阵的填充问题很有意义.循环矩阵作为一类很重要的矩阵,已有众多学者对它的特殊结构及性质等进行过深入研究,它在编码理论、数理统计、滤波算法、结构计算、数学图像处理,压缩感知等方面都有着广泛的应用[19-22].一个n×n的循环矩阵C具有如下形式:
其中c0,c1,…,cn-1∈C.显然,循环矩阵完全由第1行来确定,是一种特殊形式的Toeplitz矩阵.尽管循环矩阵很常见,但近些年针对它的填充方法却很少.循环矩阵的特殊结构导致一般的循环矩阵均是满秩的,而对于矩阵填充问题,通常使用的是低秩矩阵,因此需要生成一个低秩的循环矩阵,余和王曾在[23]中给出生成低秩循环矩阵的方法,还提出矩阵填充的均值保结构算法.由之前已有的矩阵填充算法可知,当前很多算法需要计算矩阵的SVD.而循环矩阵具有特殊的性质:它可以通过二维离散傅立叶变换进行对角化[24].与标准(例如MATLAB的eig函数)求特征值的方法相比,使用FFT计算循环矩阵特征值是非常快的,其算法复杂度为O(nlog2n),而标准方法的算法复杂度为O(n3).因此,基于FFT 来研究循环矩阵的填充问题十分有意义.本文我们主要研究循环矩阵填充的快速傅里叶变换算法.首先给出一些定义.
定义1(Fourier矩阵) 设矩阵
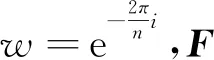
定义2(奇异值分解(SVD)[25]) 秩为r的矩阵X∈Rn1×n2,则必存在正交矩阵U∈Rn1×r和V∈Rn2×r,满足
X=UΣrVT, ∑r=diag(σ1,…,σr)
其中
σ1≥σ2≥…≥σr>0.
定义3(奇异值阈值算子[7]) 对于任意参数τ≥0,矩阵的秩是r,X∈Rn1×n2,则存在X=UΣrVT,奇异值阈值算子Dτ定义为
Dτ(X)=UDτ(Σ)VT,Dτ(Σ)=diag({σi-τ}+)
其中
定义4(硬阈值算子[26]) 给定λ≥0,硬阈值算子ηh定义为
其中变量x∈R,λ是阈值.
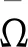
此外,定义一个位移矩阵:
(2)
本文的结构如下:第1节首先简单回顾已有算法,然后详细给出低秩循环矩阵填充的快速傅里叶变换算法;第2节通过数值实验与CMA算法比较来验证新算法的有效性和精确性;最后在第3节对全文进行总结.
1 算法
在这一节中,为了数值实验中算法比较的需要,我们首先对已有算法进行简单回顾.
1.1 矩阵填充的SVT算法
奇异值阈值算法[7]求解如下优化问题:
(3)
s.t.PΩ(X)=PΩ(M),
Cai等在[7]中,理论上证明了当τ→时,优化问题(3)的最优解收敛到优化问题(1)的最优解.其算法如下:
算法1 SVT算法[7]
第1步:给定下标集合Ω,样本矩阵PΩ(M),参数τ,步长δ,误差ε,初始矩阵Y0=k0δPΩ(M),k:=0;
第2步:计算矩阵Yk比阈值τ大的SVD:
[Uk,Σk,Vk]τ=svd(Yk).
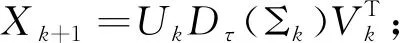
第3步:若‖PΩ(Xk+1-M)‖F/PΩ(M)≤ε,停止;否则,转第4步;
第4步:Yk+1=PΩ(Yk)+δPΩ(M-Xk+1).
1.2 循环矩阵填充的算法
1.2.1 循环矩阵填充的均值保结构算法
算法1对循环矩阵等带有特殊结构的矩阵进行填充时不能保持矩阵原有的结构,因此,对算法中产生的迭代矩阵做均值处理来确保循环矩阵的结构.其算法如下:
算法2循环矩阵填充的均值保结构算法[24](A mean value algorithm for circulant matrix completion,简称CMA)
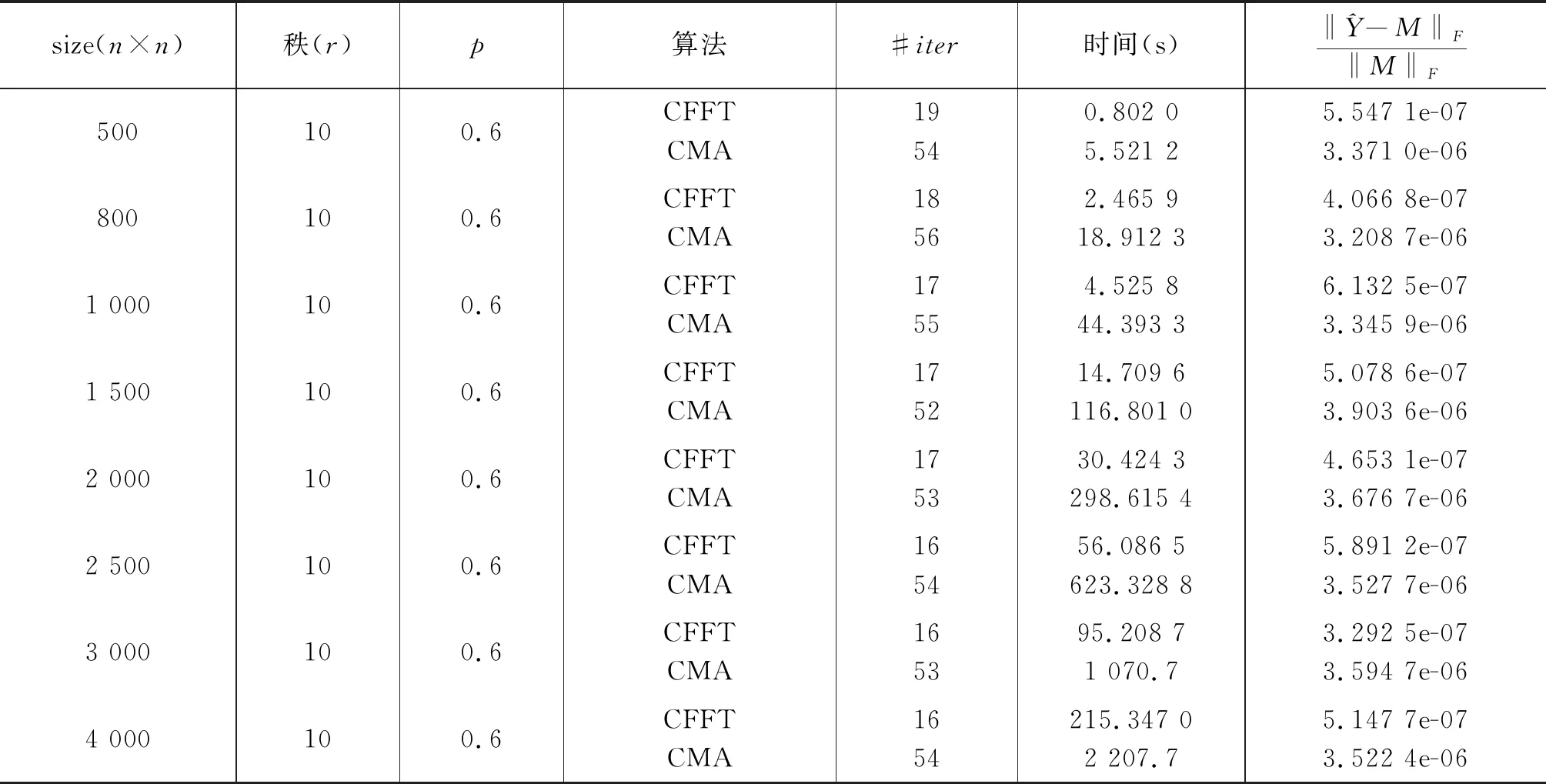
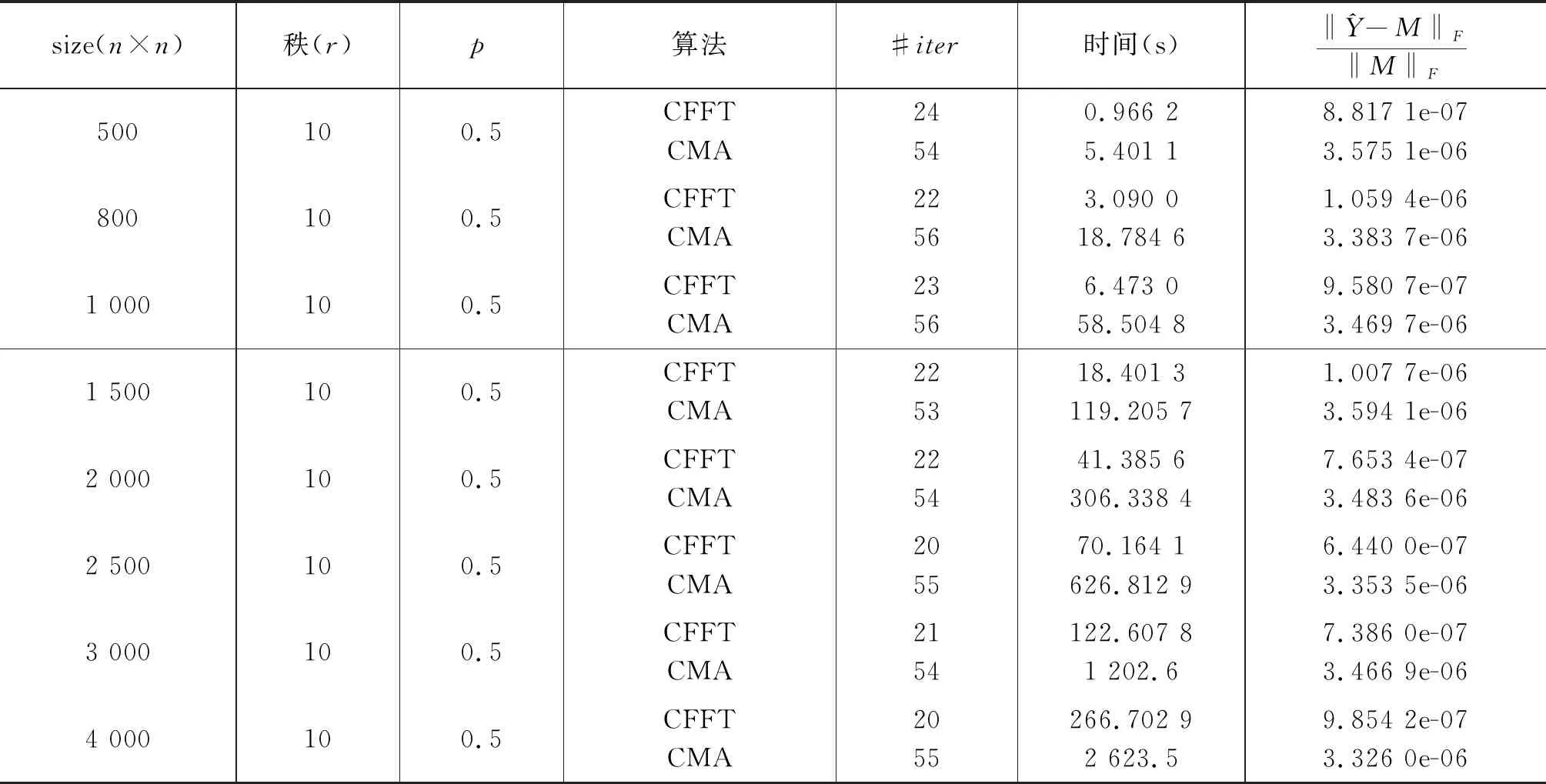
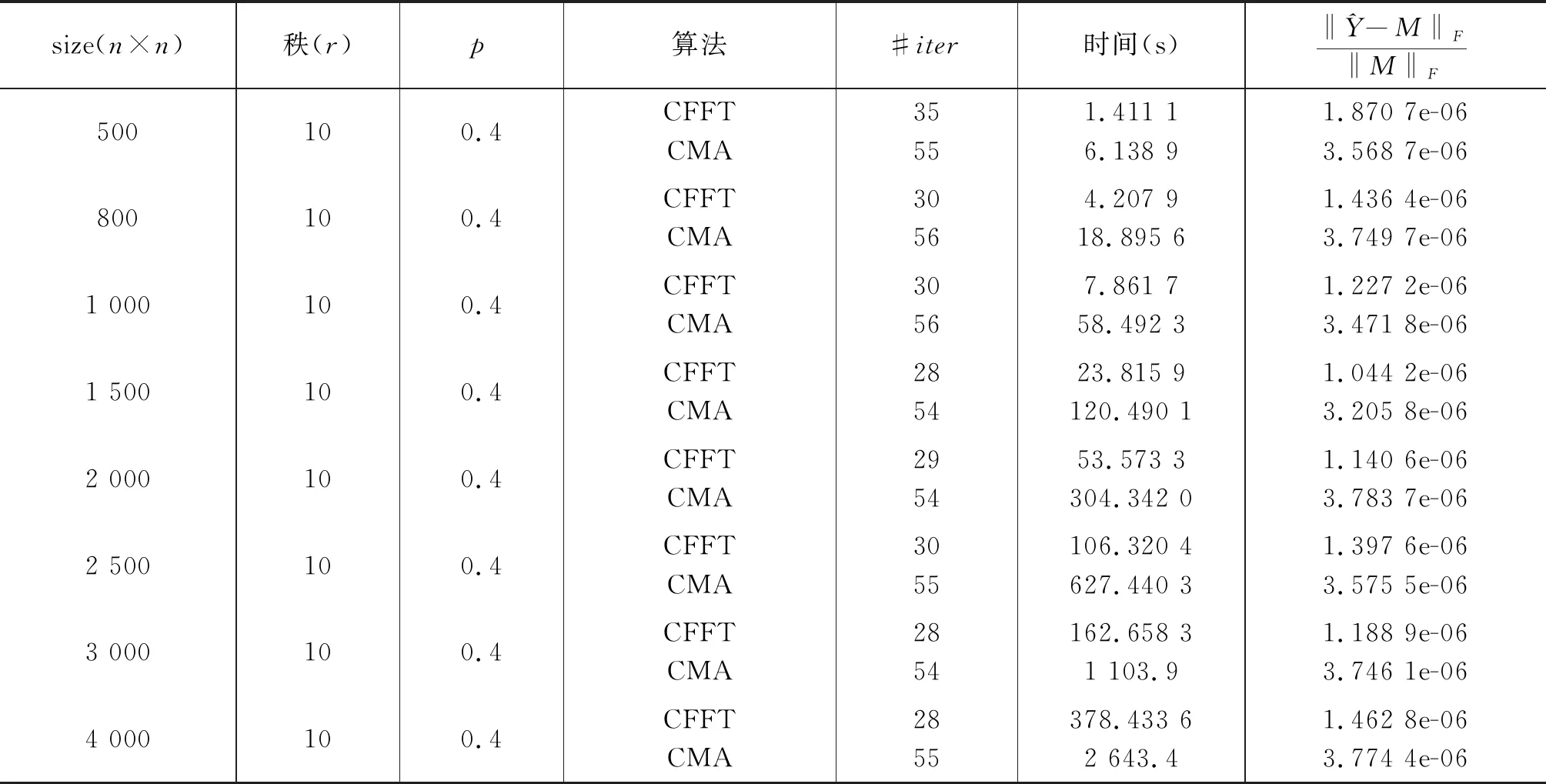
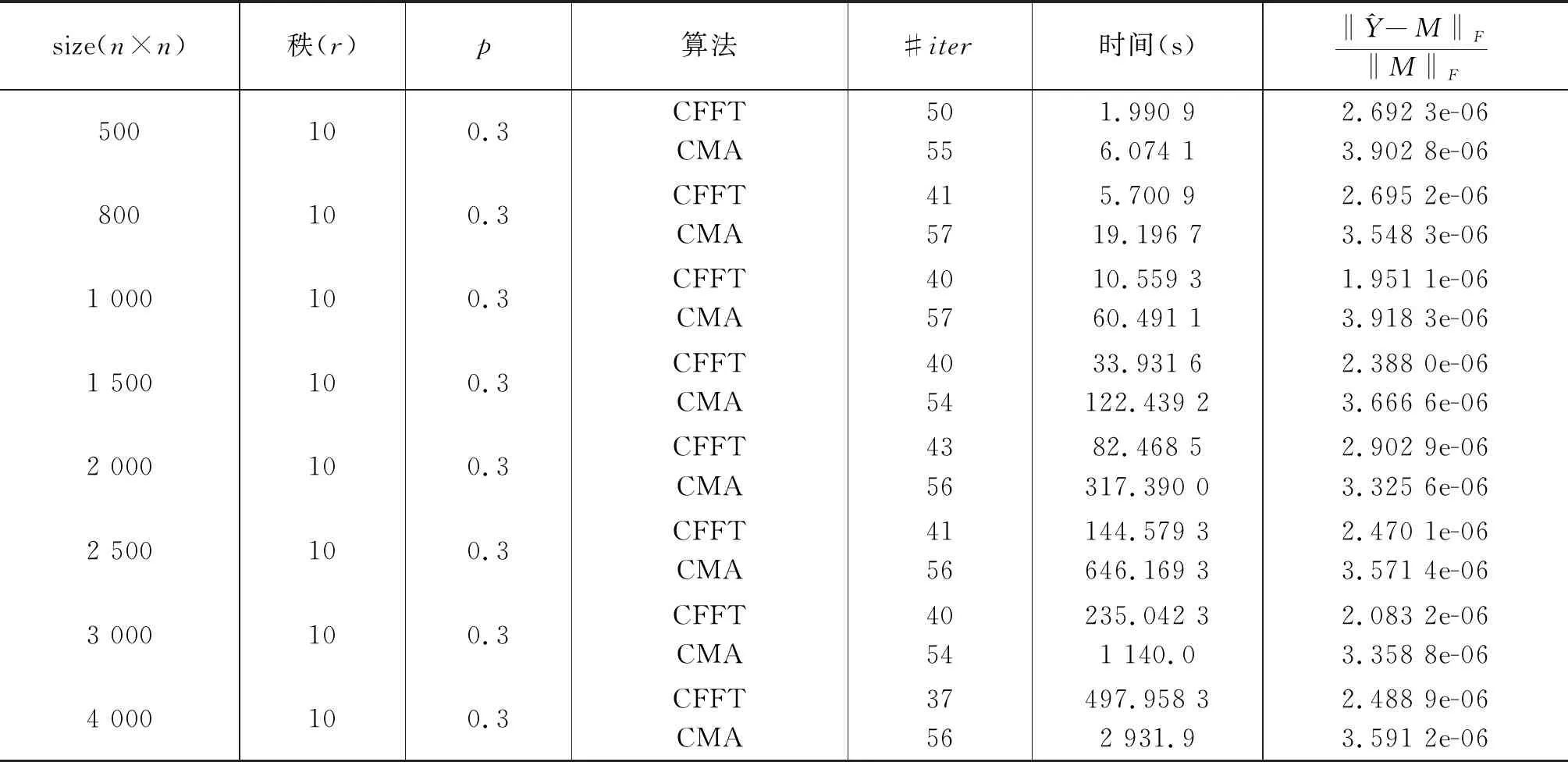
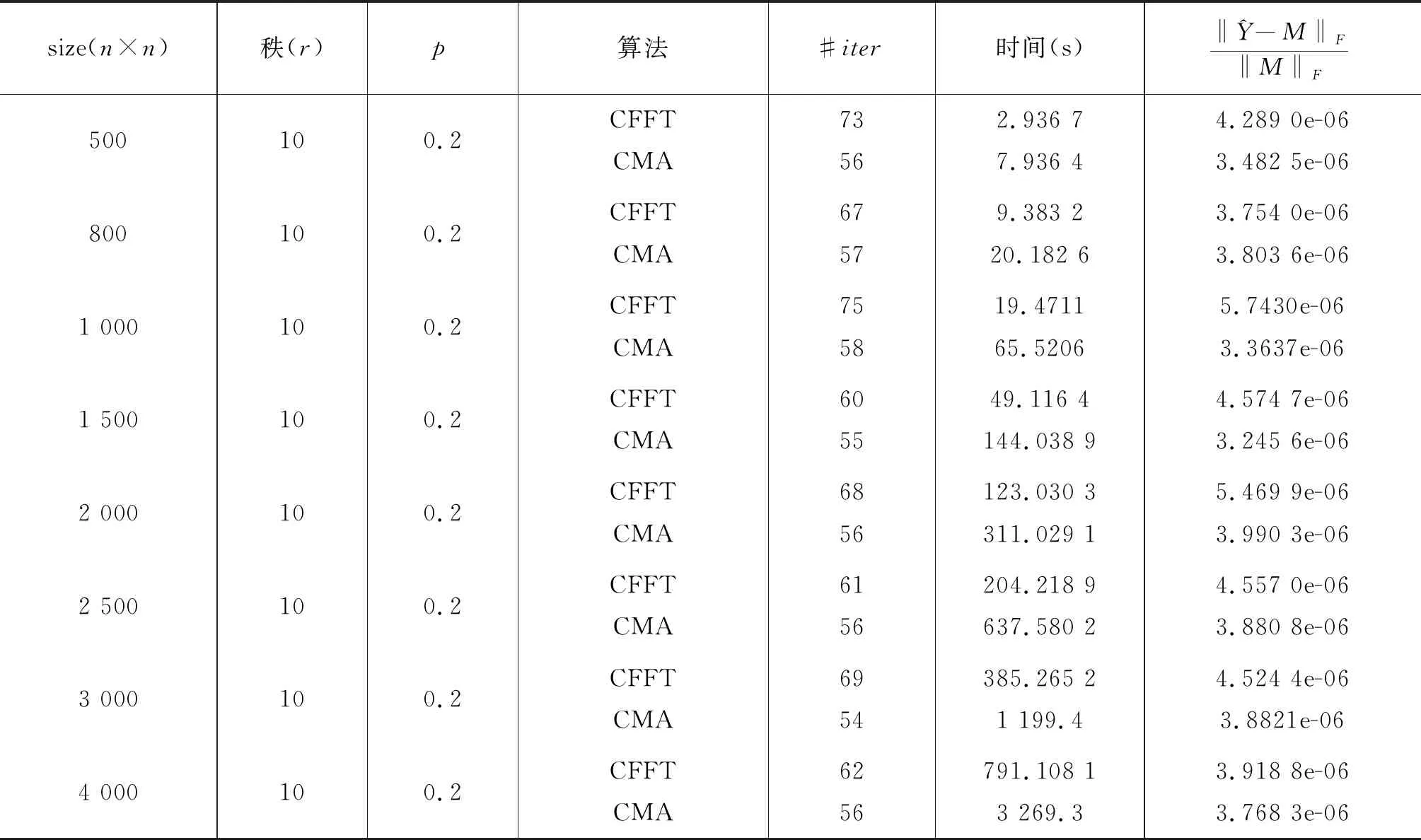
初始化:Ω是下标集合,PΩ(M)是样本值,τ0为参数,c为常数且0 第1步:对矩阵Yk进行奇异值分解: [Uk,Σk,Vk]τ=svd(Yk). 第2步:计算 Rl是(2)中的Rl且令 第3步:若‖Yk+1-Yk‖F/‖Yk‖F<ε,停止;否则τk+1=cτk,k:=k+1,转第1步. 1.2.2 循环矩阵填充的快速傅里叶变换算法 算法3循环矩阵填充的快速傅里叶变换算法(Fast Fourier Transform Algorithm for Circulant Matrix Completion,简称CFFT) 第1步:将傅里叶变换矩阵作用到矩阵Yk,求Yk的特征值 第3步:若‖Yk+1-Yk‖F/‖Yk‖F<ε,停止,否则k=k+1;转第1步. 注:该算法第1步中的τk为定义4中的硬阈值算子. 在本节中,通过数值实验给出CFFT算法和CMA算法对低秩循环矩阵填充的比较结果.这里所有的数值实验都是在相同的工作环境下进行的,即实验中所取的M和PΩ(M)具有相同的数据. 从5个表中我们看到CFFT算法在时间上总是优于CMA算法的.针对相同大小的矩阵而言,随着采样率p的增加,CFFT算法的迭代次数和运行时间都明显减少;针对相同的采样率而言,随着矩阵大小的变化,CFFT算法的运行时间比CMA算法都少,特别是矩阵阶数越大越明显,这些都说明新算法的有效性和可行性. 表1 CFFT算法与CMA算法的比较(当p=m/n=0.6时) 表2 CFFT算法与CMA算法的比较(当p=m/n=0.5时) 表3 CFFT算法与CMA算法的比较 (当p=m/n=0.4时) 表4 CFFT算法与CMA算法的比较(当p=m/n=0.3时) 表5 CFFT算法与CMA算法的比较(当p=m/n=0.2时) 在本文中,我们针对低秩循环矩阵提出一种新的填充算法,即快速傅里叶变换算法.在新提出的算法中,根据循环矩阵的特殊结构和性质,利用快速傅里叶变换求其特征值比原算法中直接求奇异值节省了大部分时间,能够有效地填充矩阵.这些都是基于实循环矩阵而言的,对于低秩复循环矩阵的构造与填充,将是我们后期研究工作的重点.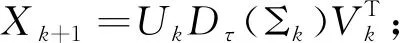
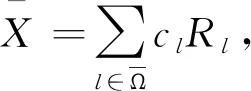
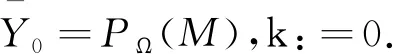
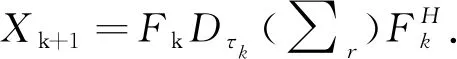
2 数值结果
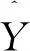
3 总结

