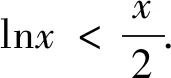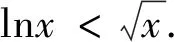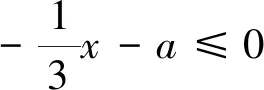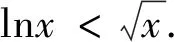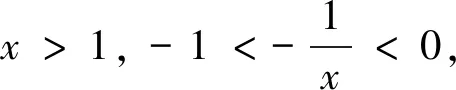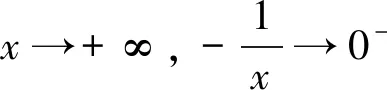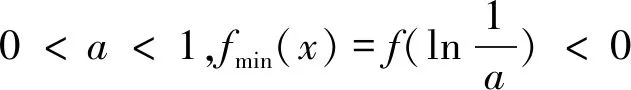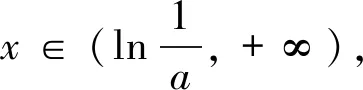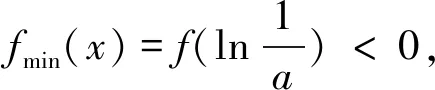放缩法求函数的零点 *

福建省泉州市第七中学 (362000) 黄永生 纪建灵 杨 丹

纵观2015年至2018年全国Ⅰ卷解答题导数部分试题，函数的零点问题一直倍受命题人青睐.为严谨地运用零点存在性定理，标准答案经常会出现匪夷所思的取点.本文尝试从放缩法的尺度和方法入手，呈现标准答案中未呈现的取点过程，并形成可操作的有效方法，希望对读者有所帮助.限于篇幅，本文仅关注试题的取点部分.

1.放缩法

要寻找f(x)<0的一个解，需将f(x)放大到g(x)，只要能找到g(x)<0的一个解即可；同理，要寻找f(x)>0的一个解，只需将f(x)缩小到g(x)，找到g(x)>0的一个解即可.

2.放缩原理

(1)存在x0∈R+,使得当x>x0，有lnx0);

(2)存在x0∈R+,使得当0-xα(α<0);

(3)存在x0∈R-,使得当x

注：上式中的α均可根据需要取值.

3.放缩法的尺度问题

例1若函数f(x)=lnx-x-a有两个不同的零点，求实数a的取值范围.

解：依题意，易知f(x)在(0,1)单调递增，在(1,+∞)单调递减.即fmax(x)=f(1)=-1-a.

若函数f(x)有两个零点，当且仅当下列三个条件同时成立:

①f(1)=-1-a>0.②∃x1∈(0,1),使得f(x1)<0.③∃x2∈(1,+∞),使得f(x2)<0.

这里仅以条件③为例讨论放缩法的尺度问题.

放缩一：由于x∈(1,+∞)时，根据放缩原理(1)得lnx<2x.所以f(x)=lnx-x-a<2x-x-a=x-a.令g(x)=x-a<0，得x

两种放缩都是将lnx进行放大，但是得到的结论相去甚远，原因在哪？仔细分析，当x→+∞时，函数f(x)<0，g(x)>0，h(x)<0.放缩一得到函数g(x)改变了原有函数f(x)的变化趋势！据此，可以得到以下关于放缩法尺度问题的一个结论：不论是将函数f(x)放大(缩小)，应当保证放大(缩小)得到的函数g(x)在自变量x趋向于定义域某端点时，具有与函数f(x)相同的变化趋势.所以，在将函数f(x)放缩之前，应当运用极限，判断函数f(x)中各项的正负，并把握好函数f(x)的整体变化趋势.同时也可以明确要取的点的区间的大致范围.基于此，例1条件③还可以有其它取点方法，例如：

4.放缩法的几种技巧

(1)利用代数式的正负性，舍项放缩

例2 当a>0时，请取一个数x∈(0,+∞)，使f(x)=ex+x2-ax>0.

分析：当x→+∞,ex>0,x2>0，要将函数f(x)缩小，可将正数项舍去.

解：当x→+∞,ex>0,x2>0，所以f(x)=ex+x2-ax>x2-ax，令x2-ax≥0，得x≥a.取x0=a，则f(x0)=f(a)=ea+a2-a2=ea>0.

评析：本例中ex>0,x2>0，要取一个数使f(x)>0，舍去ex,x2中哪一项都可以，只是保留x2得到的不等式更容易解.但是不能将ex,x2同时舍去，否则得到-ax就是一个负数，本质上改变了函数f(x)在x→+∞时的变化趋势.

(2)利用放缩原理，调整放缩

例3 已知a<-1，取一个数x∈(1,+∞)，使得f(x)=alnx+x-a2>0.

分析：当x→+∞,x>0,alnx<0，要将函数f(x)缩小，不能简单将alnx舍去.由于x→+∞时，f(x)→+∞，可将alnx缩小.

评析：本例中为了将参数a消去，可取x0=ea，但此时x0=ea∉(1,+∞).当函数f(x)均存在正负项时，应当在保证函数f(x)整体变化趋势不变的前提下，根据放缩原理进行局部的调整放缩.

(3)利用局部限制，放缩无穷小量

5.高考试题应用举例

例5(2016全国Ⅰ卷理21)函数f(x)=(x-2)ex+a(x-1)2，试说明已知a>0，fmin(x)=f(1)<0时，f(x)有两个零点.

分析：当x→-∞，(x-2)ex为反向无穷小量，考虑局部限制放缩；当x→+∞时，(x-2)ex>0，

a(x-1)2>0，考虑舍项放缩.

解：易知a>0时，f(x)在(-∞,1)单调递减，在(1,+∞)单调递增.

令(x-2)ex≥0，解得x≥2.取x0=2，则f(2)=a>0.

分析：当x→+∞时，ae2x>0，(a-2)ex<0，-x<0，考虑根据放缩原理调整放缩；当x→-∞，(a-2)ex为反向无穷小量，考虑局部限制放缩，ae2x>0，考虑舍项放缩.

当x∈(-∞,0)时，0(a-2)ex-x=(a-2)-x.