一道高考题的源、解及其它

广东省佛山市高明区高明实验中学 (528500) 林建雯广东省深圳市南头中学 (518052) 田彦武

一、问题呈现

已知函数f(x)=aex-lnx-1．

(1)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

该题为2018年全国新课标Ⅰ卷文科第21题，题目着重考查应用导数研究函数的问题.题目所涉及到的知识点有应用导数研究函数的单调性，应用导数研究函数的极值与最值，利用单调性证明不等式等.本题很好的考查了数学逻辑推理和数学基本运算能力以及用数学语言表达数学问题的能力，特别是第(2)小问，学生可通过对已知函数解析式进行观察、比较、综合、抽象与概括，进而构造新的函数再次运用导数解决不等式，以此来考查学生创新能力及综合运用数学知识分析问题和解决问题的能力．

导数进入中学教材，给传统的中学数学教学带来了生机和活力，为中学数学研究提供了新的视角、新的方向、新的方法和新的途径，可以说在函数命题这一块开辟了新的空间.函数与导数的综合问题所涉及的知识和数学思想方法丰富，与函数、导数、方程、不等式等众多主干知识联袂会具有新颖别致、不落俗套等特点.同时，此类题目引入参数后，更深层次的蕴含数形结合、分类讨论、构造等数学思想方法，综合考查学生的各种能力.特别是自然对数函数和以e为底的指数函数在近几年的高考数学命题中很受命题者的青睐和器重！有时这两种函数也会同时出现！以全国Ⅰ卷文科数学第2问为例来说：2018年不等式证明，2017年已知不等式恒成立求参数取值范围问题，2016年函数零点问题，2015年证明不等式，2014年不等式有解问题，2013年单调性、极值，2012年不等式恒成立问题，2011年证明不等式等．但是，无论怎么考，讨论单调性都是考查的重点.

二、问题的源

1.源自课本

本题第(2)问的设计完全取自于人教A版数学选修1-1第三章《导数及其应用》第3.3单元《导数在研究函数中的应用》中的习题3.3B组题：

利用函数的单调性，证明下列不等式，并通过函数图象直观验证：

(3)ex>1+x，x≠0；

(4)lnx0.

其实，我们对不等式(3)和(4)的条件放宽并变形，会得到如下不等式：

(3)′ex≥1+x，x∈R；

(4)′lnx≤x-1，x>0.

关于考题与课本题目的关系我们在下文中详细讲解.

2.源自高考题

仔细对比发现2015年全国高考Ⅰ卷文科第21题第(2)问和本题第(2)问有异曲同工之处，函数解析式的特点也好，还是第(2)问的解法也罢，的确比较类似.原题如下：

设函数f(x)=e2x-alnx．

(1)讨论f(x)的导函数f′(x)零点的个数；

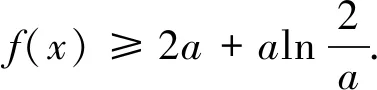
从课本中改编题目，从往年高考中改编题目，是高考命题一贯的原则，所以认真研究课本中的例题、习题，特别是B组的部分题目，认真研究往年经典的高考题目，是我们教学中的重要一环。关于本题和2015年考题之间的关系及其解法，请读者自行研究，这里就不再赘述了.

三、问题的解

下面我们给出文首高考题的解法：

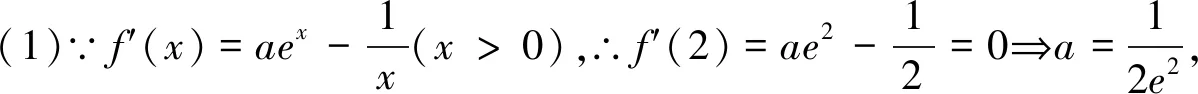
第(2)问是本题的关键与核心所在，方法比较多，以下提供三种证法：

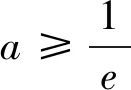
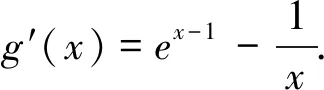
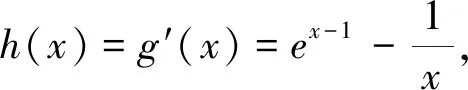
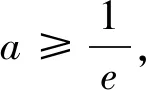
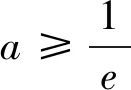
目前，这一传统文化习俗虽然不如过去那样热烈浓厚，广泛得到传承，但在梅里斯达斡尔族区已成为节日活动，每逢正月十六这一天，达斡尔族学会都要组织活动，载歌载舞庆祝这一具有达斡尔民族特色的传统节日。

我们先证明不等式：ex-1≥x.此即为不等式(3)′.令g(x)=ex-1-x，则g′(x)=ex-1-1，当x∈(0,1)时，g′(x)<0，g(x)为减函数；x∈(1,+∞)时，g′(x)>0，g(x)为增函数.则g(x)min=g(1)=e0-1=0，即ex-1≥x．

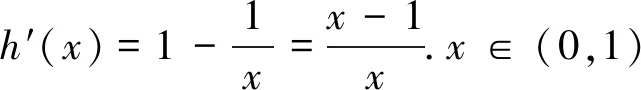
点评：本证法很好的利用了课本中的那两个不等式，可以说这个高考题完全取自于教材而又高于教材，这是高考命题的基本原则之一.而上述证法也很漂亮直接.当然，上述两个不等式画图也很容易理解.

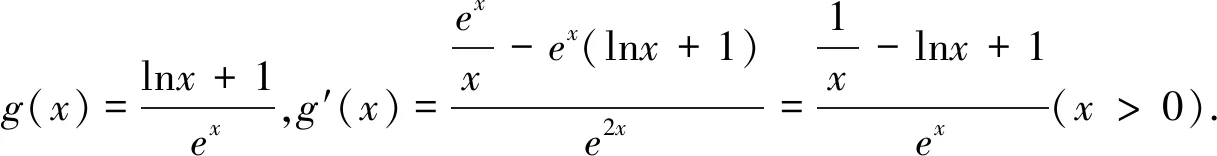
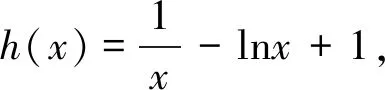
点评：本证法也是我们解决恒成立问题一贯采用的方法和手段，即分离参数，转化成求最值问题.这个思路简单，容易想到，难点在于构造新的函数，研究新的函数的最值问题，需要学生有很好的运算能力和意志品质，要有耐心和耐力以及自信心等.

四、问题的拓展

其实，只要我们认真研究会发现，2019年天津高考文科第20题，也正好包含了自然对数函数和以e为底的指数函数，所研究的方法和手段基本一致，但又略高于文首的高考题.可以说天津的考题应该是命题者在充分研究全国Ⅰ卷文科的这道高考题目后所命制出来的一道题目.不同的是在设问上有所不同，涉及到函数的零点和极值点偏移问题，具体解答请大家自行研究，此处不再赘述了.

设函数f(x)=lnx-a(x-1)ex，其中a∈R.

(Ⅰ)若a≤0，讨论f(x)的单调性；

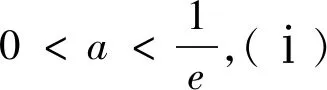
另外，以下不等式也是很重要的一个不等式，在函数与导数的命题中会经常出现，读者可自证.

求证：ex≥x+lnx，x>0.

五、教学建议和反思

新一轮课程改革和教材改革正在进行中，与以往相比，这次更具有深远意义．特别是在这其中提出了六大数学核心素养和很多新的教学理念，如《课程标准》提倡注重提高学生的数学思维能力，并指出：“人们在学习数学和运用数学解决问题时，不断地经历直观感知、观察发现、归纳模拟、空间想象、抽象概括、符号表示、运算求解、资料处理、演绎证明、反思与建构等思维过程．这些过程是数学思维能力的具体体现，有助于学生对客观事物中蕴涵的数学模式进行思考和作出判断．”因此，教师在教学中处理题目时不能就题论题，应该正确引导学生认真挖掘题目的内涵和外延，使学生认识到编题者编写这些题目的意图，这不仅不断完善学生的数学知识结构和认知结构，而且能激发学生对教材题目研究的兴趣，这对培养学生的探究能力、创新能力和实践能力是大有裨益的．《课程标准》同时指出：“高中数学课程应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质．数学课程要讲逻辑推理，更要讲道理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴涵在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态．”因此，“在教学中，如何从课本例习题出发，进行变式教学，无论从方法还是内容上都起着‘固体拓新’之用，可收到‘秀枝一株，嫁接成林’之效，同时可培养学生提出问题和解决问题的能力，并使学生的探究能力和创新能力得到发展．”

其实，从上述对题目的渊源分析及解法分析来看，这样的命题风格不仅章显了命题人的智慧，而且还警示我们用题海战术处理高考复习是徒劳的，教师必须高瞻远瞩地研究和探讨历年高考经典试题，分析这些题目的背景及更深层次的东西，挖掘其数学思想和方法，从内涵和外延两个角度去认识和理解，这样我们的高考复习既高效，又省力．