基于引导线偏移的建筑网格生成方法
王奇胜, 高博青, 吴 慧
(1. 浙江大学 建筑工程学院, 杭州 310058; 2. 浙江财经大学 公共管理学院, 杭州 310018)
随着计算机辅助设计技术的突破和建造工艺的提升,世界各地出现了越来越多的自由曲面建筑,如上海阳光谷世博轴[1]和天津于家堡综合交通枢纽站[2].该类建筑通常具有独特的造型需求,常规的网格结构难以表达,而已有的自由曲面网格设计方法,要么耗时耗力,要么适用范围有限.为复杂的自由曲面生成符合建筑要求的网格,是现代空间结构研究的难点与热点.Owen[3]总结了经典的网格划分算法,如Delaunay法[4]、波前法[5]、映射法[6]及其组合[7-8].但这些方法在自由曲面上的应用有局限性,无法满足建筑上对网格规整、流畅的要求.近些年,针对自由曲面网格生成的研究,取得了一定的进展.Su等[9]在波前法中引入主应力线来控制网格走向,生成均匀的三角形网格,但网格的流畅性较差.Zheleznyakova和Wang等[10-12]采用基于物理模拟的方法优化节点分布,再结合Delaunay法和映射法生成空间网格,但对于曲率较大的曲面,网格容易产生映射畸变.Gao等[13]在曲面的参数域中以直线段为引导线调控网格走向,采用两种方法推进引导线并结合曲面的参数化关系生成流畅的空间网格,称为映射引导线法.但是,该方法仅适用于空间域和参数域对应关系较好的曲面,否则易引起网格畸变.
为了生成规整、流畅、走向可控的建筑网格,基于引导线偏移的思想,提出一种自由曲面网格划分方法,即空间引导线法.通过直接在曲面上偏移曲线避免了映射畸变,引入偏移距离函数实现了曲线间距的控制,并通过与两种现有方法的对比说明空间引导线法的优势.
1 曲线偏移
1.1 非均匀有理B样条技术
非均匀有理B样条(Non-Uniform Rational B-Splines,NURBS)[14],是建筑上常用来表达自由曲面的技术.NURBS曲线、曲面是由节点矢量、控制点、权值确定的参数方程,通过调整这3个变量可以实现几何形状的自由变化.对于边界复杂的自由曲面,常用裁剪曲面表达.裁剪曲面是由完整的NURBS曲面和用于裁剪的NURBS曲线联合表示的曲面.
基于NURBS技术,针对曲线和曲面的几何操作,如曲线延伸、曲面延伸、线线求交、线面求交、曲线拟合等,都已有成熟的算法实现,在Rhinoceros、3DS Max等软件中有着广泛的应用.
1.2 基本算法
引导线是直接在曲面上勾勒的曲线,一般由建筑师给定.在曲面上偏移引导线时,偏移得到的曲线(偏移线)必须要保证本身在曲面上、端点在曲面边界线上,与引导线走势一致且间距合理.鉴于已有的曲线偏移方法难以满足上述要求,本文提出一种在曲面上偏移曲线的方法,偏移引导线的过程如图1所示.
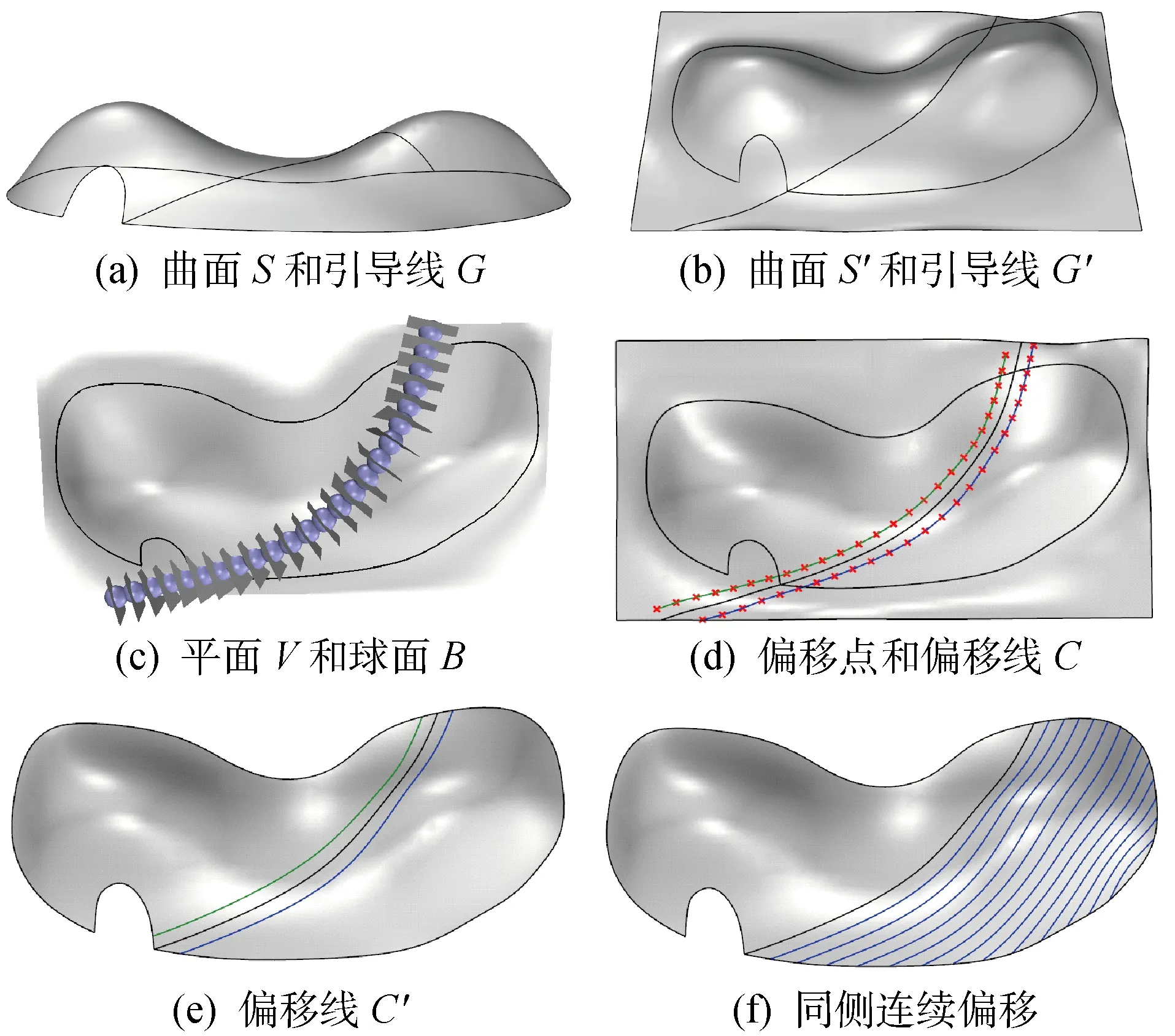
图1 偏移引导线的过程
以图1(a)所示的曲面S为例,为了保证后续生成的偏移线有足够的长度,先延伸曲面S(裁剪曲面取其完整曲面进行延伸)和引导线G,得到曲面S′和在曲面S′上的引导线G′(图1(b)).在曲线G′上布置n个点作为偏移的基准点,记为点集P.过点集P中一点p,生成垂直曲线G′的平面V,同时以点p为球心、偏移距离为半径生成球面B(图1(c)).求平面V、球面B和曲面S′的交点,若交点存在,则作为点p在引导线两侧的偏移点q.遍历点集P中的点,得到由偏移点q组成的点集Q.将点集Q中在同一侧的偏移点按顺序拟合成曲面S′上的曲线C(图1(d)).裁去曲线C不在曲面S上的部分,得到偏移线C′(图1(e)).在引导线的同一侧上,以刚生成的偏移线为引导线,采用上述方法生成新的偏移线,如此迭代,得到一组偏移线(图1(f)).
在上述过程中,基准点的数目和间距需要合理设置.数目过大或间距过小时,会导致偏移线不光滑且运算更耗时;数目过小或间距过大时,会导致偏移曲线不能体现引导线的形态.实践表明,根据偏移距离控制基准点的数目和间距,使相邻的球面B正好有少量的重叠,可以取得相对较好的计算结果.
1.3 间距控制
通过调控各基准点的偏移距离,可以控制偏移线与引导线的间距.当各基准点对应的偏移距离R都等于基本间距s时,上述偏移为等间距偏移,反之为不等距偏移.等间距偏移有助于后续生成均匀、规整的网格,所以更为常用;合适的不等距偏移可以得到间距按一定规律变化的曲线组.这可为建筑师提供一种更加灵活的选择,有一定的应用前景.为实现间距的等比、等差或自定义规律的变化,下面构造相应的基准点偏移距离函数.
采用横向(沿引导线走向)比例rh和纵向(垂直引导线方向)比例rz来实现偏移距离的等比调控.第j次偏移的引导线上第i个基准点pij对应的偏移距离为
(1)
当rh=rz=1时,生成等间距偏移线;rh≠1时,生成间距沿横向渐变的曲线,如图2(a)中的曲线分布为下侧较密,右上侧较疏;rz≠1时,生成间距沿纵向渐变的曲线,如图2(b)中靠近初始引导线的相邻曲线间距较小,远离的曲线间距较大.图2中的曲线虽然间距不同,但间距变化自然,疏密有致,具有一定的美感.
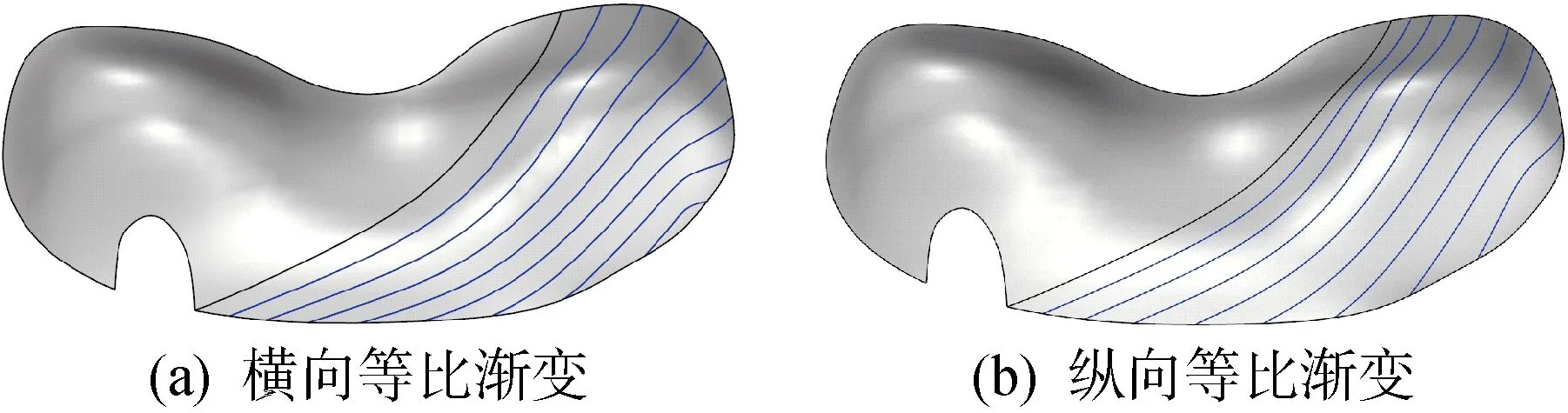
图2 偏移间距的调控
类似地,采用横向差值ah和纵向插值az实现偏移距离的等差调控.基准点pij的偏移距离为
Rij=s+ah(i-1)+az(j-1)
(2)
除了等比和等差调控外,也可根据需要自定义偏移距离函数R(s,hi,zj),实现曲线间距的特定调控,其中hi和zj是跟基准点编号i、j有关的函数.
1.4 形态优化
在曲面较为平坦且引导线弯折不显著时,由上述方法偏移得到的曲线一般都较为光顺,但当偏移距离相对引导线或曲面的曲率半径较大时,拟合的偏移线可能较不光顺,甚至出现交叉.以图1(a)所示的曲面S为例,由初始引导线迭代地朝两侧偏移得到的曲线如图3(a)所示.图中圈出的曲线(红线)存在扭曲、自交的情况.为此,对上述偏移算法进行局部调整,将满足下式的相邻偏移点合并为两者的中点:
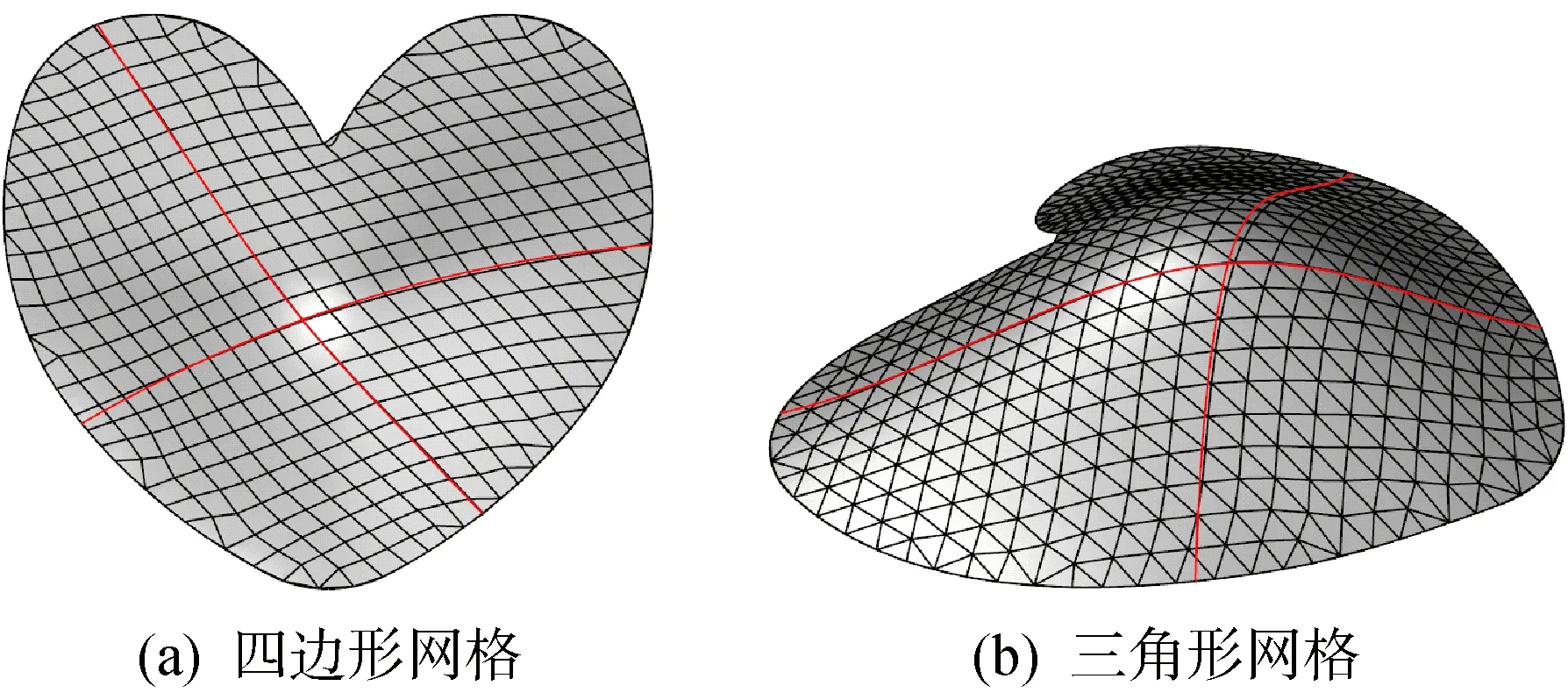
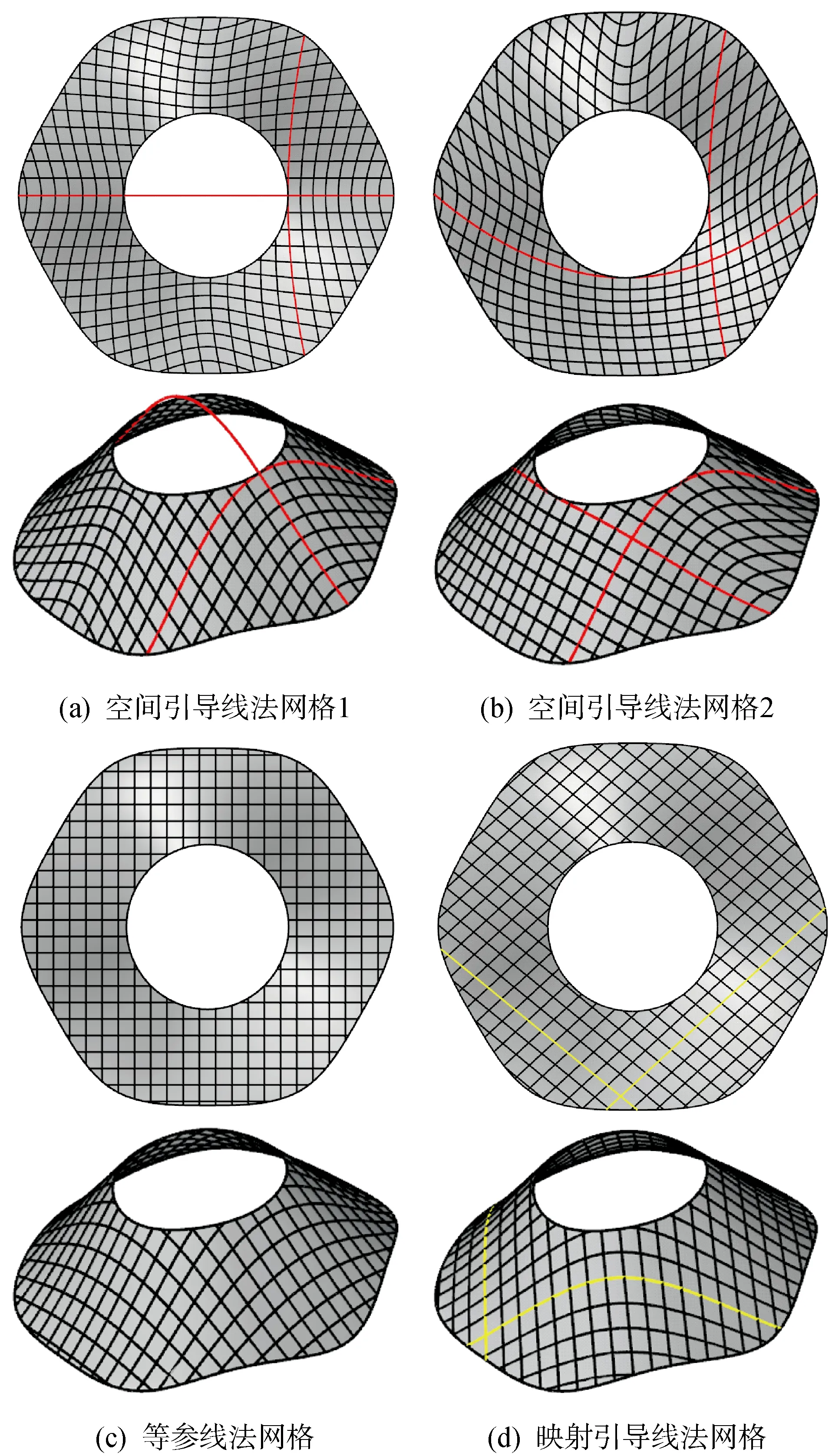
di,i+1 (3) i=1,2,…,n-1 式中:k为调整系数,一般取0.5;Ri和Ri+1分别为第i和第i+1个基准点的偏移距离;di,i+1为第i和第i+1个基准点对应的偏移点之间的距离. 通过合并距离过近的偏移点,优化了偏移线的形态,避免了曲线弯折突兀,甚至交叉的情况出现.优化后的偏移线形态光顺,与引导线的间距合理、走势吻合,如图3(b)所示. 图3 偏移线的形态优化 基于给定的单条引导线,在曲面上迭代地进行偏移后,得到一组布满整个曲面的偏移线.以偏移线(包括初始引导线)为网格线,直接按照一定的规律进行分解和连接,形成最终的网格.例如,先按相同杆长将偏移线等分,再用曲面上的约束Delaunay法将分段点连接成三角形网格(见图4(a)).此外,也可以采用其他方法在曲面上生成另一组曲线,使其与偏移线相交而构成网格.例如,由等距断面线(曲面上的等高线)与偏移线构成网格,如图4(b)所示. 由于偏移线已经基本决定了网格的走向和布局,所以基于引导线偏移生成的网格能较好地反映建筑师的要求,体现建筑意蕴. 图4 基于单引导线生成的网格 如果勾勒了两条相交的引导线,那么分别对这两条引导线迭代地进行偏移,得到两组偏移线.通过求交、连线等操作,将这两组偏移线构成的曲线网转换为四边形网格,如图5(a)所示.若需要三角形网格,则先在延伸的曲面上采用上述方法生成四边形网格,再连接四边形的对角线形成三角形网格,然后将不在原曲面上的部分剔除,得到曲面上的三角形网格,如图5(b)所示. 图5 基于双引导线生成的网格 通过布置双引导线,建筑师可以从两个方向上引导网格走向,控制网格形态,往往比单引导线能更好地表达建筑美感. 基于双引导线偏移生成的网格,虽然在整体上较为规整、流畅,但在边界附近存在杆长参差不齐、节点数目较多的缺点.为此,可以合并边界上相距较近的节点并采用基于弹簧-质点模型的网格松弛方法[15]调整网格形态,得到如图6所示的网格.调整后的网格仍保持原来的网格走势,且边界附近的杆长均匀性得到提升,节点数目明显减少,但线条的流畅性降低,以致建筑美感下降.鉴于调整前后的网格各有优劣,建筑师可以根据需求进行选择. 图6 调整后的网格 图7是一个外边界近似为圆角六边形、内边界近似为圆形的裁剪曲面,且其参数域为自身的水平投影.分别以两对相交的曲线为引导线,采用空间引导线法生成两组不同的网格,如图8(a)和(b)所示.参数设置完毕后,空间引导线法仅需数秒即可完成曲面的网格划分,而生成的网格既规整又流畅,能较好地体现建筑意蕴. 作为对比,采用现有的等参线法和映射引导线法[13]对图7中的曲面进行网格划分.等参线法是按一定间距提取NURBS曲面的等参线,形成四边形网格,如图8(c)所示.映射引导线法是在曲面的参数域中等间距偏移直线段,再映射到曲面上形成网格,如图8(d)所示(图中黄线对应于参数域中的直线段).这两种方法得到的网格也具有相对较好的流畅性,但参数域中很规整的网格,在映射到曲面后由于尺度的非均匀变化而使其规整性明显下降.此外,这两种方法难以调控网格走势或调控能力有限. 图7 给定的曲面和引导线 图8 采用3种方法生成的网格 因此,与现有方法相比,空间引导线法避免了映射畸变,提高了网格的规整性,提升了对网格走势的调控能力,更符合建筑网格设计的需求. 为生成符合建筑意蕴的网格,提出了空间引导线法.首先,确定合适的曲线作为引导线并在其上布置适量的基准点.接着,在过基准点垂直引导线的平面内,求取以基准点为圆心、偏移距离为半径的圆与曲面的交点,作为偏移点,并遍历各基准点,得到两组在不同偏移方向上的偏移点.将两组偏移点按顺序分别拟合成两条曲面上的曲线,作为偏移线.然后,以这两条偏移线为引导线,分别向两侧推进生成新的偏移线.如此迭代,在曲面上生成一组按特定间距分布的网格线.最后,通过分段、连线等操作,以偏移线为网格线生成流畅网格.通过偏移距离函数调控偏移线的间距;通过合并过近的偏移点,优化偏移线的形态;通过布置两条引导线,从两个方向上控制网格走向.与两种现有网格划分方法的算例对比表明,空间引导线法既保证了较好的网格流畅性,又避免了映射畸变,能得到更规整的网格,还能更灵活地调控网格走势.
2 生成网格
2.1 单引导线

2.2 双引导线

3 分析和比较

4 结语

