基于自适应离散粒子群算法的机翼调姿基准点优化布局

高井涛 郑子君

(南昌航空大学航空制造工程学院，江西 南昌 330063)

在飞机数字化装配中，机翼的装配变形通常是由多个离散的调姿基准点的位置误差来表示的，不同的调姿基准点布局所包含的机翼变形不尽相同，不合理的基准点布局将会降低机翼的位姿评价精度，增加装配变形估计误差，而引起机翼变形的主要原因之一是其自身重力。因此，为了提高装配精度，如何布置调姿基准点引起了航空界的普遍重视。Shukla[1]等把由遗传算法选出的测量点作为产品的关键特征，利用其几何尺寸容差为产品诊断偏差模型提供参考。王鹏[2]通过NX 二次开发实现了9mm 点与圆孔中心点的选取，然后构建预测矩阵来判别不同检测点的贡献度，通过剔除贡献度较少的检测点提高检测效率。

1 调姿基准点优化模型的建立

在飞机机翼的装配中，机翼的总装配变形由多种工艺影响因素共同造成，其变形一般由机翼上布置的基准点位置误差来表示。设检测点数量为e，并布置在机翼上e 个不同的部位，则各偏差源所造成的机翼装配变形模式可表示为：

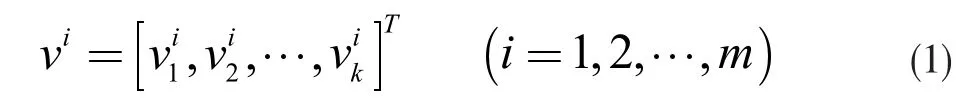
因此机翼由多偏差源导致的变形可表示为:

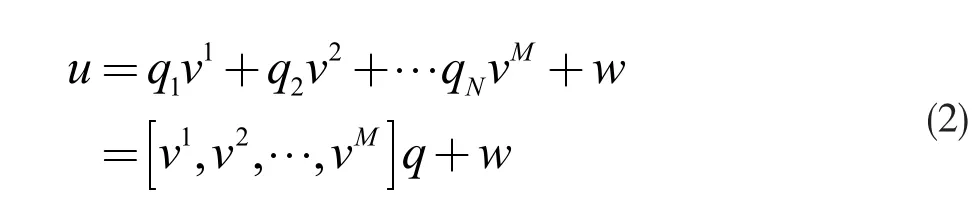
式中，q 表示个体贡献值，w 表示高斯白噪声。

本文实验条件有限，因此机翼的变形因素仅考虑重力这一个因素，机翼变形重新定义为：

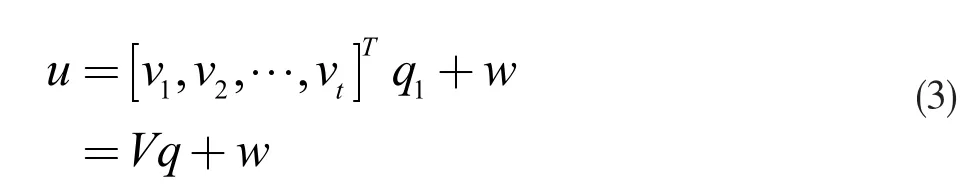
式中，V 为变形模式矩阵。

由式3 可定义q 的估计矩阵q'为

式中，q'的精度取决于随机误差水平。

从统计学角度评价q'的估计精度，即q'的协方差矩阵为

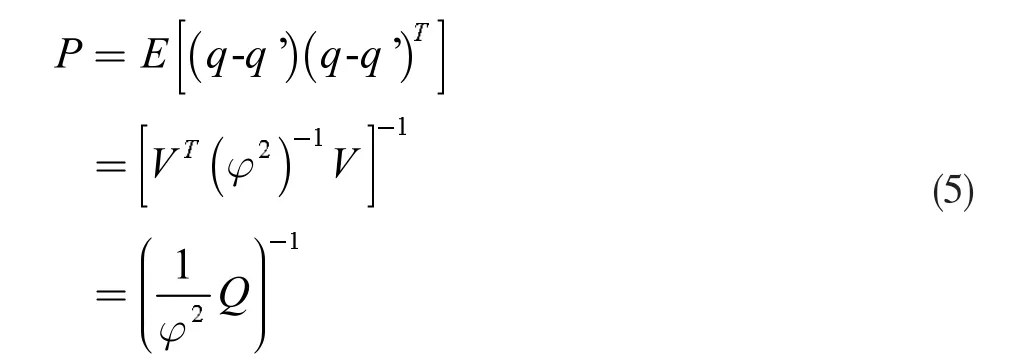
式中，E 表示数学期望值，φ 是噪声矢量w 的协方差矩阵，Q 为费希尔信息矩阵。

当Q-l和V-l删除基准点l 后，由有效独立法[3]可知基准点l 的有效独立性指标可表示为：

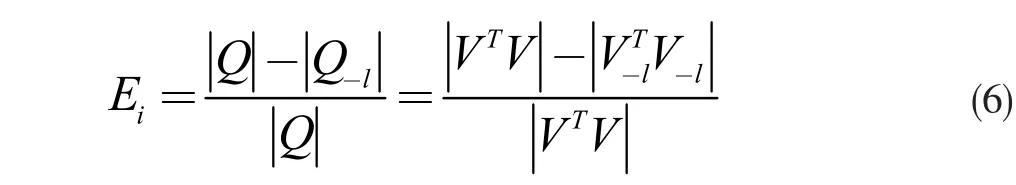
由式（6）可知，每个迭代中都会淘汰有效独立性指标最小的基准点，经过不断迭代更新，最终剩下符合要求的基准点，从而获得最优基准点集。

式（6）通常可以实现从e 个检测点中优选出b 个基准点组成基准点集D，但优选效果较差，本文采用自适应离散粒子群算法改善传统检测点优选方法的效率低下和寻优效果，目标函数如式（7）所示。

2 调姿基准点布局的优化技术

2.1 优化模型

为了提升机翼位姿的测量精度，根据式(8)可以选取符合系统要求的基准点数目：

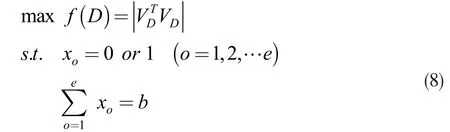
式中，e 为初始待选基准点数目，b 为优选基准点数目。

2.2 自适应离散粒子群算法

设离散粒子群算法在一个n 维的目标搜索空间中，有D 个粒子组成种群，则第i 个粒子位置可表示为Xi=(xi1,xi2,...xin)，第i 个粒子的速度可表示为Vi=(vi1,vi2,...vin)，(i=1,2,...,D)。第i 个粒子的最优位置成为个体最优值可表示为Pb=(pi1,pi2,...pin)，整个种群的最优位置即为全局最优值为gb=(g1,g2,...gn)，更新粒子位置和速度值：

其中：t 为迭代次数，c1和c2为学习因子，r1和r2是[0,1]内的随机数，vij表示为粒子的速度，xij表示为粒子的位置，i=1,2,...,D，j=1,2,...,D。

文中采用一种动态自适应惯性权重[4]，通过对粒子当前的适应度值f 进行评价调整ω，当f＞fa，此时目标函数值较差，因此为了使其向较好的搜方向靠拢，应当使惯性因子要大;当f-a＜f＜fa时，此时目标函数值较稳定，这里可不改变惯性因子的值; 当f＜f-a时，粒子的目标函数值比较好，此时则选用较小的惯性因子。改进后ω 可定义为:

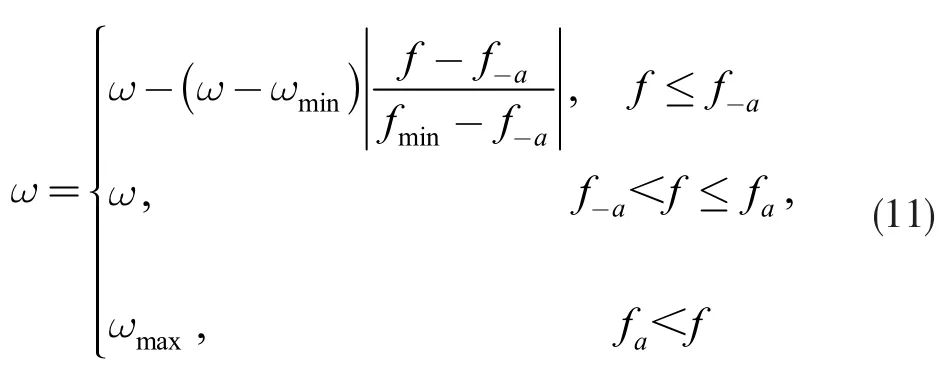
式中，ωmax表示为ω 的最大值，ωmin表示为ω 的最小值; fmin表示当前所有粒子的最小适应值，fa表示当前所有粒子的平均适应值。f-a表示将所有小于fa的适应值相加取平均数。

本文的自适应离散粒子群算法的粒子在迭代过程中，其取值变化只限于0 和1，因此粒子位置xij更新公式可如下做如下变化：

式中，r 表示从(0,1)内的随机数，粒子速度vij取值为1和0 的概率分别为s(vij)与1-s(vij)。

2.3 自适应离散粒子群算法基本步骤

2.3.1 自适应离散粒子群算法参数初始化。

2.3.2 计算个体的适应度值，当选取的基准点数量大于约束条件时，对适应度值进行惩罚计算，获得粒子个体最优位置p 和粒子的最优值pb，以及粒子的种群全局最优位置g 和种群全局最优值gb。

2.3.3 自适应惯性因子的更新，计算相应的适应度值，判断是否替换粒子个体最优位置p 和最优值pb，以及全局最优位置g 和最优值gb。

2.3.4 判断是否满足边界条件，若满足边界条件，搜索过程结束，输出全局最优解；否则，继续更新迭代，如图1。

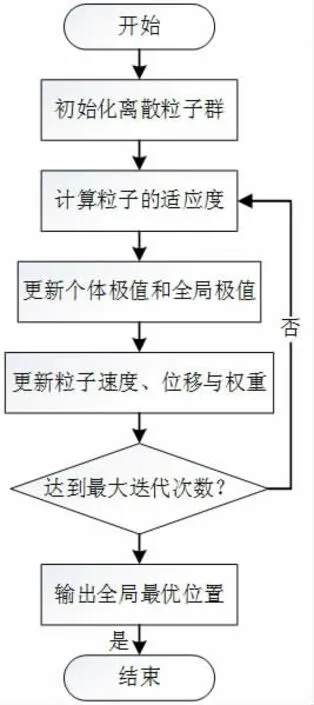
图1 自适应离散粒子群算法流程

3 实例分析

3.1 机翼有限元分析

机翼实际结构过于复杂，难以分析，因此对机翼与工艺接头的结构进行合理简化为翼肋、梁和蒙皮三部分，其中，该机翼共有3 个梁，10 个翼肋，机翼外廓尺寸为1060mm×350mm×55mm。工艺接头尺寸40mm×20mm×20mm，如图2 所示。

图2 机翼简化结构分析图

图3 机翼有限元模型

机翼有限元模型的单元类型为C3D8R，网格密度为5mm，其材料选用的是7075-T7451 铝合金，弹性模量与泊松比分别为72GPa 与0.33，工艺接头定义为刚体。机翼各个零部件之间是绑定约束。

3.2 机翼调姿基准点布局优化结果

首先设置自适应离散粒子群优化算法的初始参数，种群规模p=300，学习因子c1=c2=0.7，迭代次数K=5000，初始惯性权重ω=0.9，开始对检测点布局进行优化，一般来说，机翼装配时的测量基准点数量应不少于4 个，因此本文分别将基准点个数设置为10，12。同时文中还计算了基于经典离散粒子群算法的基准点布局优化以验证自适应离散粒子群算法的有效性，从两种算法运行结果看出，当自适应离散粒子群算法与经典粒子群分别实现10、12 个基准点优化布局时的目标函数值依次为0.1715 与0.17154、0.2329 与0.2329，并分别在迭代2218与2574、1955 与2503 代就已经收敛，具体的优化过程如图4、5 所示。

图4 布设10 个基准点时两种算法的优化效果

通过比较图4，图5 以及上述分析可以发现两种方法适应度值比较接近，但是传统的经典粒子群算法往往需要更多的计算时间，其收敛速度较低，而自适应离散粒子群算法运行时间快，收敛性能更好，说明该优化算法具有较好的寻优效果。通过自适应离散粒子群算法和经典离散粒子群算法优化后，在布设10 个基准点时，其基准 点 编 号 分 别 为5、37、60、75、107、122、140、174、186、191 与5、37、60、75、107、122、140、172、186、191。在布设12 个基准点时，其基准点编号分别为5、37、60、75、84、107、122、128、140、174、186、191 与5、37、60、75、84、107、122、129、140、174、186、191。从结果来看，自适应离散粒子群算法得到的基准点布局体现出了很好的继承性，即优化后的12 个基准点布局完全包含优化后的10 个基准点布局。

图5 布设12 个基准点时两种算法的优化效果

4 结论

机翼的装配变形通常用调姿基准点的位置误差来表示，基准点的不同位置的装配变形信息也不同。为了获得更多的变形信息，通过最大化费希尔信息矩阵行列式的值，实现了在机翼上的最优基准点位置。为了有效地解决基准点的最优布局问题，提出了基于自适应离散粒子群算法的基准点优化布局方法，并与基于经典离散粒子群算法的基准点优化布局方法进行了比较，结果表明，基于自适应离散粒子群算法的基准点具有更好的寻优效果。影响装配变形的其他因素很多，如装配车间的环境温度、零件的制造误差、工装的非标称位置等。每个因素都会导致不同程度的装配变形，最终影响整机装配质量。本文仅考虑机翼自身重力引起的变形模式，对基准点的布局进行优化，其他影响大部件装配质量的变形因素也值得深入研究。