基于形态反演的小尺度磁性目标三维重建方法
尹 刚, 张 林
(中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 621000)
小尺度磁性目标的三维重建是以磁性体在测量面产生的磁异常信号为先验信息,对磁性目标的三维形状、位置、磁导率(磁化强度)等参数进行求解,进而实现磁性体三维姿态的准确重建.其在重要军事目标的精确识别[1]、未爆弹销毁[2]、航天器内部磁性分布研究[3]等领域均具有十分重要的实际应用价值.
目前国内外对小尺度磁性目标三维重建技术的相关研究仍处于起步阶段,类似的磁源反演技术主要应用于地质勘探方面,可分为三维形态反演和物性反演[4].形态反演是在测量面下半空间场源体给定磁性参数大小的基础上,利用观测异常数据来拟合几何体(如多边形或多面体)形状,通过几何体的形态大小模拟目标体的三维姿态.物性反演是将观测区域对应的测量面下半空间离散成规则的长方体单元,通过反演的方法估计每个离散单元的磁性值,由磁性的分布勾绘出场源的三维姿态.形态和物性反演均可实现目标的三维重建,但物性反演需要求解关于未知磁性参数的欠定方程组,存在解不唯一且不稳定的问题[5].
尽管小尺度磁性目标的三维重建问题可以借鉴地质勘探中的磁源反演技术,但是两者又存在一定的差别:首先磁性目标的三维重建问题对磁性参数反演的精度要求更高;其次在参数反演的基础上需要勾绘出磁性目标的三维姿态.因此,本文在借鉴地质勘探领域磁源形态反演技术的基础上,建立适合小尺度磁性目标的三维重建技术.利用比磁总场数据信息更为丰富的磁梯度张量数据[6]进行磁性目标的三维重建,首先对测得的磁梯度张量数据进行倾斜角、局部波数和Helbig估计计算,得到磁性目标水平方向和垂直方向的大致分布范围和近似磁化方向;然后对磁性目标待反演空间进行网格划分,确定初始模型并建立待增长模块集,进而在待增长模块集中选择最优的增长模块对当前模型进行迭代更新;通过模型的不断增长最终实现磁性目标的三维重建.
1 模型初始化及最优增长模块的选择
为得到较为准确的形态反演结果,本文采用不求解反演方程,而是在待反演空间的所有解中找到一个最优解的方法.其基本思想是:首先利用测得的磁梯度张量数据建立磁局部异常特征和磁性目标边界的相互关系,利用倾斜角[7]和局部波数[8]计算,估计得到磁性目标水平和垂向的大致分布范围,进而确定较为紧凑的磁性目标的待反演空间范围并进行网格划分;然后利用Helbig方法[7]估计磁性目标的近似磁化方向,在网格中选定一个长方体作为初始模型并对其磁化强度赋值,建立待增长模块集,并使该模块集中的每一个长方体至少有一个面与当前模型中的面重合,进而通过一定的选择机制在待增长模块集中选择最优的增长模块对当前模型进行迭代更新;通过模型的不断增长最终实现磁性目标三维形状的构建.故小尺度磁性目标三维重建的算法流程如图1所示.

图1 形态反演算法流程
在磁性目标三维模型的迭代更新中,需要依据一定的选择机制选择最优的增长模块,为此,建立模块选择函数,每次均选择待增长模块集中使得模块选择函数取值最小的长方体作为最优增长模块:
Γ(m)=φ(m)+ρφ(m)+κθ(m)=
(1)
式中:m为长方体的磁化矢量;N为形态反演时使用的磁梯度张量分量的个数;ρ,κ为正则因子,用以调整目标函数中3项的相互比例;φ(m)用相关性计算确保反演模型产生的磁梯度张量数据与测得的磁异常数据在整个测量区域上的整体相似性,并克服φ(m)约束可能出现的异常点问题,φ(m)为反演模型产生的磁梯度数据与测得的磁梯度数据之间的差值,可克服仅仅用φ(m)约束可能存在的整体偏大或整体偏小问题,θ(m)通过计算长方体单元之间的距离来约束反演模型,使其具有较好的整体性且不朝某一个方向无限延伸.φk(m)表示第k个磁梯度张量分量在整个测量区域上的整体相似性,φk(m)为反演模型产生的第k个磁梯度张量分量数据与测得的该磁梯度张量分量数据之间的差值.具体计算公式为
(2)
式中:cov(·)表示求协方差;D(·)表示求方差;dk为在测量平面内测得的磁梯度张量的第k个分量的数据向量,Fk为对应第k个分量的核函数矩阵,由单个长方体的磁梯度张量正演公式计算得到[9];Δx, Δy, Δz为当前模型在3个方向上的宽度;M为当前模型所包含的长方体个数;lj为待选择增长模块中心与当前模型中第j个长方体中心之间的距离;ζk为尺度因子,可由磁梯度张量数据的测量值和正演值求解得到,求解公式为
(3)

由形态反演算法流程可得模型增长示意,如图2所示,并且在寻找待反演空间中最优解的过程中存在以下约束准则:
(1) 模型增长是连续的,新得到的待增长模块至少有一个面与当前模型共面,且每一个当前模型都存在一个待增长模块集,最优增长模块必须从待增长模块集中选择.
(2) 待增长模块集中包含的每个模块均至少有一个面与当前模型共面(如图2所示),当前模型迭代更新时,待增长模块集也要同时更新.
(3) 整个待反演空间中每个网格的磁化强度只有0和预设值m两种选择.
磁性目标形态反演的过程即为反演模型所产生的磁梯度张量场一步步地逼近已知测量数据的过程,并且模型的每次增长都是当前模型最优的,因此,可以认为形态反演所得到的目标模型具有较高的可信度.
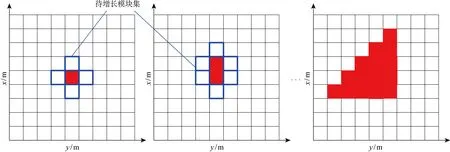
图2 形态反演中模型增长二维示意图
2 迭代终止准则的建立
在整个形态反演过程中,每次均选择待增长模块集中使模块选择函数取值最小的长方体作为最优增长模块以更新反演模型,更新过程是持续的.因此,需要建立适当的目标函数,当目标函数达到事先设定的阈值时,则终止模型的迭代更新,得到的当前模型即为形态反演得到的磁性目标的三维形状.迭代终止准则的建立方式有多种,其中一种为建立迭代过程中的目标函数,表达式为
(4)
式中:φnew(m)和φnew(m)为加入最优增长模块后的计算值;φold(m)和φold(m)为加入最优增长模块前的计算值;τ为比例因子,以调整式(4)前后两项的重要度.
当目标函数小于事先设定的阈值δ时,则表明增加一个长方体对磁性目标模型产生的磁异常场与测量值之间的拟合度的贡献较小,此时终止模型的迭代更新.
迭代终止的判断还可以利用测量面上磁梯度张量各分量真实值与反演估计值之间的方均根误差(RMSE)随模型增长步数的变化规律来实现[10].当反演过程从初始模型向真实物体接近时,随着模型增长步数的增加,各张量分量的RMSE逐渐变小,直至反演模型最接近真实物体时,各张量分量的RMSE达到最小值.此时若继续进行模型增长计算,各分量的RMSE将逐步增大.因此,在模型增长过程中,磁梯度张量分量真实值与反演估计值之间的RMSE极小值点可作为模型迭代增长的终止点,其对应的反演模型即为形态反演得到的磁性目标的三维形状.
另外,当实际测量数据中存在较大的测量噪声时,将导致ξ(m)的取值始终都较大且张量分量估计值与理论值之间的RMSE随步数增大的变化规律不明显.此时,可结合倾斜角计算得到的水平边界约束范围进行判断,若估计得到的磁性目标模型已远远超出倾斜角估计得到的水平边界范围,则认为测量数据中噪声较大导致阈值δ较小,需终止迭代过程重新选择δ进行形态反演.

图3 磁性目标在测量平面内产生的磁梯度张量场及张量不变量
3 模拟分析
为验证所提形态反演方法用于磁性目标三维重建中的有效性,以空间中存在的磁性长方体为例进行数值模拟实验.其中,长方体中心坐标为(0,0,10 m),边长分别为12,12和8 m,考虑较为一般性的情况,设置磁化强度为40 A/m,磁化方向的倾角和偏角分别为20° 和35°.建立z方向竖直向下为正的右手坐标系,考虑实际中运动磁梯度张量系统的测量条件,设置水平x和y方向上的采样间隔均为2 m,则在z=-1 m平面测得的磁性目标产生的磁梯度张量的6个分量Bxx、Bxy、Bxz、Byy、Byz、Bzz和计算得到的张量不变量(Normalized Source Strength, NSS)[11]如图3所示.
计算得到的倾斜角[7]如图4所示,由于该磁性目标的磁倾角较小,计算的得到的倾斜角I1和I2均出现正负伴生的现象,而I3并未出现此种情况,所以,模拟实验以倾斜角I3的识别结果进行目标反演空间的水平约束,取水平方向上x和y的约束范围均为 -8~8 m.
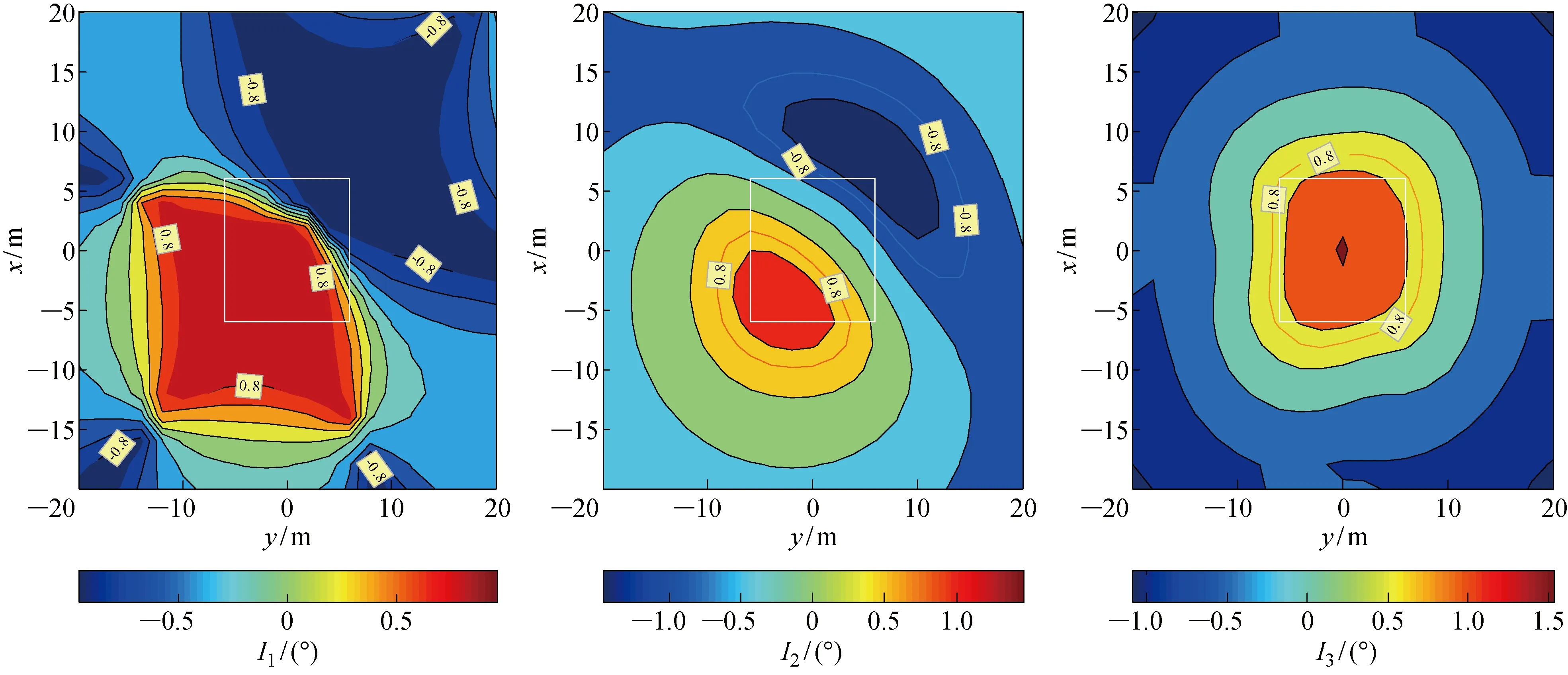
图4 计算得到的倾斜角
值得注意的是,在此得到的磁性目标反演空间的水平约束并非磁性目标的水平边界,而是要大于目标的水平边界,一方面是为了避免水平边界识别存在的误差导致反演空间较小,另一方面是为了给待反演空间划分长方体单元模型预留空间余量.另外,尽管磁梯度张量异常数据的水平方向测量范围为 -20~20 m,但通过倾斜角识别得到磁性目标存在的近似水平区域,将反演空间范围大幅度减小,在提高反演效率的基础上也可以有效提高反演精度.
基于Helbig方法估计得到的磁性目标的磁倾角和磁偏角[7]及不同窗口时计算得到的多个磁倾角和磁偏角方差的倒数如图5和图6所示,计算时滑动窗口大小选择为:3×3~7×7.由图5和图6可知,Helbig方法不仅准确估计得到了磁性目标的中心位置,也估计出了磁性目标的磁倾角为20° 和磁偏角为35°.
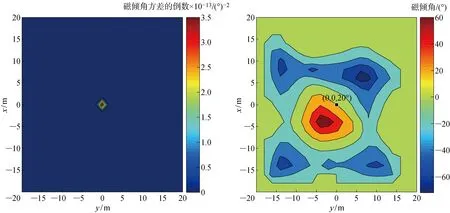
图5 磁倾角方差的倒数及磁倾角的平均值
利用局部波数[8]计算得到的磁性目标的垂向位置的分布情况如图7所示,图中直方图颜色仅用于区分不同深度的估计个数,计算时滑动窗口大小选择为6×6.由图7可知,尽管反演得到的磁性目标垂向分布位置跨度较大,约为8~20 m,但其在每个深度的分布情况各有不同,从左图中可看出该目标大约集中分布在8~14 m,由右图中归一化直方图可得,在深度为14 m处时直方图总值可达到90%,为此,本实验选择垂向约束范围为0~20 m,磁性目标垂向中心位置为14 m.
选择每个长方体的大小均为2 m×2 m×2 m,然后结合图4和图7得到的反演空间范围约束及图5和图6得到的磁化方向估计结果,设定形态反演时初始长方体模块的中心位置为(-1 m,-1 m,9 m),磁化方向中的磁倾角为20°,磁偏角为35°,进而利用式(1)所示的最优模块增长函数及式(4)所示的迭代终止准则进行长方体的形态反演.

图6 磁偏角方差的倒数及磁偏角的平均值

图7 局部波数法反演得到的磁性目标的垂向位置的分布情况
为清晰地给出形态反演中模型增长的过程,图8展示了模型增长的前3步、第52~54步以及最后3步,图中蓝色直线表示真实磁性目标的外部框架,黑色箭头指示出了该迭代步数相对于前一迭代步数时的长方体增长模块.
由图可知,当初始模型给定后,其对应的待增长模块集也是确定的,后续的每次迭代,算法均自动从待增长模块集中选择最优的增长模块添加到现有模型中,同时更新待增长模块集为下一次迭代做准备.整个迭代过程中,最优增长模块的选择一直遵循式(1)所示的准则,在待增长模块集中寻找函数最小值对应的模块单元,使得每次都把待增长模块集中对反演贡献最大的长方体模块加入到当前模型中.因此,整个迭代过程即为一个优化过程,通过每一步都选择最优的增长模块进而实现最优的磁性目标形态反演.
模型增长到不同阶段时对应测量面得到的张量各分量如图9~12所示.对比不同阶段反演得到的张量分量与图3所示的长方体在测量面产生的理论张量分量可知,形态反演的模型增长过程也是磁梯度张量反演估计值接近真实值的过程.
分析模拟实验过程可知,由于式(1)中φ(m)的约束,在模型增长中的每一步,测量面得到的磁梯度张量分量反演估计值与理论值均有较高的分布相似度;由于φ(m)的约束,模型朝着反演估计值与理论值数值差异变小的方向增长;由于θ(m)的约束,保证了反演模型不朝垂直向下方向无限延伸,所以,形态反演通过模型的不断增长实现了磁性目标三维形状的重建.

图8 形态反演中模型增长过程示意图

图9 初始模型在测量面产生的磁梯度张量分量
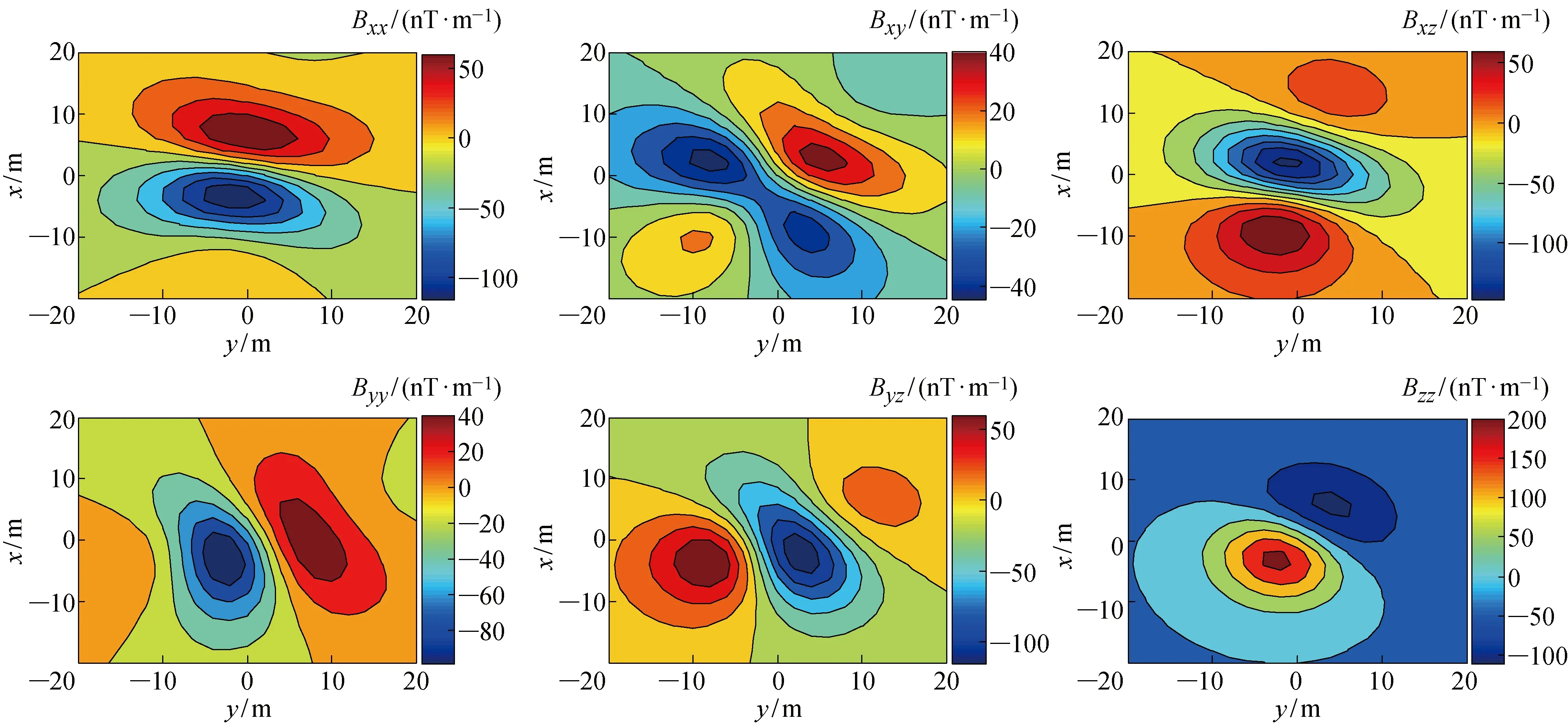
图10 模型增长到第52步时在测量面产生的磁梯度张量分量
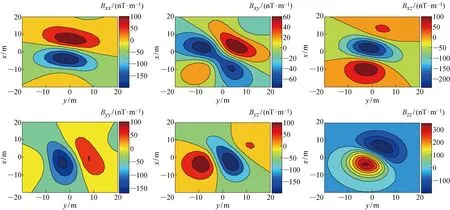
图11 模型增长到第90步时在测量面产生的磁梯度张量分量

图12 模型增长到第157步时在测量面产生的磁梯度张量分量
随着模型增长步数的增加,测量面上磁梯度张量各分量真实值与反演估计值之间的RMSE变化趋势如图13所示,该图也验证了形态反演的过程是张量分量反演估计值向真实值接近的过程这一初始算法思路,其中RMSE在模型增长到第157步时达到极小值,并且此时张量各分量估计值与真实值的RMSE接近0.因此,可选择该参数作为迭代增长的终止步数,将此增长步数下得到的反演模型作为磁性目标形态反演的最终结果.将其真实长方体的三维形状对比可得:所提形态反演方法得到的三维重建结果具有较高的可信度.当然,由于磁梯度张量数据的快速衰减特性,重建得到的磁性目标的纵向分辨率略差于横向分辨率.
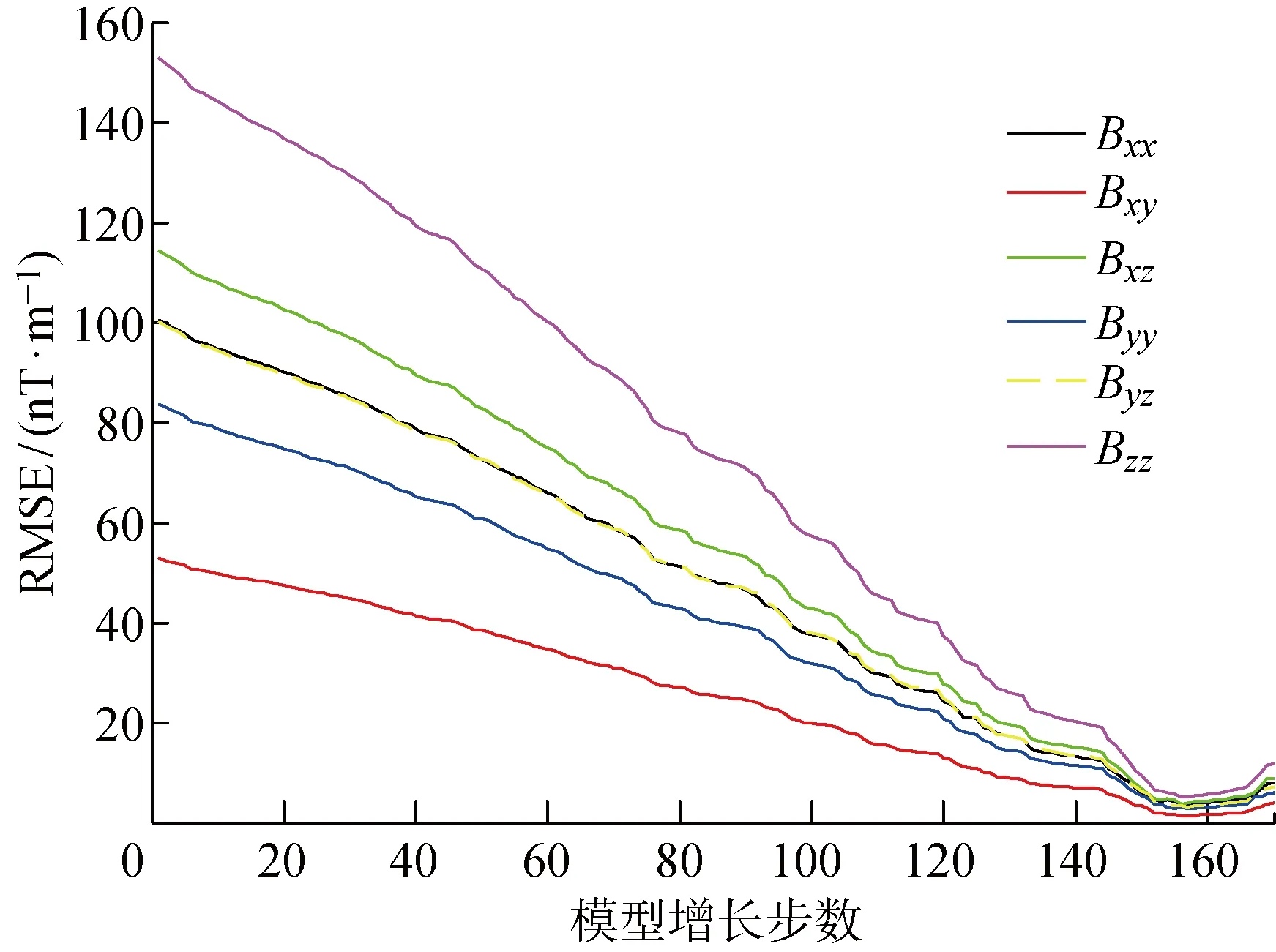
图13 测量面上张量各分量理论值与反演值之间的RMSE随模型增长步数的变化趋势

图14 长方体磁性目标的三维重建结果
为了得到直观的可视效果并反映小尺度磁性目标的三维特征,利用上述的反演结果进行三维模型的构建,三维重建结果如图14所示,尽管重建结果在长方体的棱角处存在一定的偏差,但重建结果与真实磁性目标整体上具有较高的相似度,可用于小尺度磁性目标的识别.后续可通过更为精细的网格划分,选择更小的模型增长模块,长方体棱角处的反演将更为精确.另外,值得说明的是,本文所提方法不仅仅局限于长方体状磁性目标的三维重建,可适用于任何形状的磁性目标体.
4 结语
本文针对小尺度磁性目标的三维重建方法开展研究,将地质勘探领域的反演方法扩展到小尺度磁性目标中,建立了适用于小尺度磁性目标的三维重建方法.相比地质勘探领域的磁性参数反演,本文提出的小尺度磁性目标的三维重建方法增加了反演预处理环节,即利用磁梯度张量异常场数据进行待反演空间范围和目标磁化方向等参数的估计,将反演空间缩小在磁性目标分布范围内,有效降低了反演多解性、提高了反演精度和反演速度.实验结果表明:该重建结果与真实目标相似度较高,具有较高的重建可信度和一定的工程应用价值.当然,本文仅考虑了磁性目标均匀磁化的情况,后续将重点研究非均匀磁化的磁性目标体的三维重建问题,并且将构建实际的磁梯度张量测量系统进一步验证所提重建方法的工程实用性.

