考虑动态性能退化的生产系统预防维护和缓存配置策略
郭闻雨, 张秀芳, 修玉皎, 夏唐斌, 潘尔顺
(上海交通大学 机械与动力工程学院, 上海 200240)
为了提高生产系统的可靠性,并保证其具有一定的生产加工能力,科学制定预防维护策略至关重要.然而,预防维护工作会造成设备停机,引起系统生产中断,导致相应损失.在生产系统的配置中,合理设置缓存区能有效减少因上游设备故障或上游设备维护而停机导致的下游设备空闲和生产缺货问题[1],从而降低损失成本;但缓存区的设立也会导致相关成本增加.因此,合理配置缓存容量并优化系统的维护策略,有着迫切的现实意义.

图2 第i个预防维护周期不同阶段的缓存波动示意图
目前,针对带缓存生产系统的维护策略的研究主要集中于双机系统.周炳海等[2]以“两设备带缓存区”的系统模型为研究对象,基于田口质量损失理论,综合考虑产品质量损失和缓存区的影响,建立以最小化单位运行成本为目标的预防性维护模型.Dimitrakos 等[3]假设系统中的上游设备会发生故障,下游设备为完美机器不故障,以Markov过程对上游设备的维护阈值进行优化,并证明了设立缓存区对于降低长期生产成本的作用.Meller等[4]提供了此类系统的典型应用场景,即汽车总装线,其中设备M1代表装配线,设备M2代表直接供给装配线的并行加工作业之一,系统特点在于设备M1维护导致停机而中断生产的代价高昂.Cheng等[5]在此基础上,考虑更符合实际的不完美维护,使用几何分布来描述退化过程.Gan等[6]则研究了在预防维护过程中备件与缓存区容量的联系,考虑维护或维修过程中存在备件短缺的问题,将备件响应时间也作为决策变量.Rezg等[7]建立有限时间域内包含维护、缓存和缺货的总平均成本数学模型,同时对缓存容量和维护役龄进行优化决策,并利用模拟与试验设计相结合的方法简化求解同一问题,通过对精确数学模型和模拟试验结合法的结果进行比较,证明后一种方法的准确性,为复杂系统联合优化提供了思路.以上文献在描述退化过程时,未考虑退化对设备加工性能造成的影响,因此无法全面反映设备的综合状态,也难以进一步讨论设置缓存对生产系统带来的整体影响.
本文以此类带有缓存区的双机生产系统为研究对象,引入设备动态性能退化模型,同时对缓存变化的多个阶段建模,以寿命周期内的平均总成本最低为目标,对系统的最优维护以及缓存设置进行联合决策,改善单一目标决策的不足,从而更好解决工业制造实际场景的需求.
1 问题描述
本文的研究对象如图1所示,I为生产系统的上游设备,P为下游设备,B为I和P之间的缓存区;I为P提供待加工的零部件和半成品等,具体应用如汽车总装线、座椅装配线等[4].

图1 带有缓存区的双机生产系统模型
本文全面地考虑了实际生产中随维护作业与缓存变化而形成的3个阶段:

(2) 平稳生产期.当缓存容量达到上限K之后,I的额定加工周期调整至与P一致,考虑I退化导致加工能力下降,缓存容量缓慢减少,直到I综合性能状态w降至维护阈值W.

本文假设条件如下:① I不发生饥饿,P不发生堵塞.② I在运行时可靠度和加工能力均会下降,并伴随着故障的发生,退化规律可用其可靠度和加工能力的综合状态函数表征;P退化缓慢,假设一直完好运行.③ 预防维护只能使I回到较新状态.④ 若I故障时则执行小修,可使其可靠度和加工能力恢复至故障前状态.⑤ 调整I额定加工周期时,I自身加工能力不改变.
模型参数为:ccm表示单次小修成本,小修时间忽略不计;cpm和tpm表示单次预防维护成本和时间;CR和tR表示置换成本和时间;cop1和cop0分别表示额定加工周期为T1和T0时,单位时间内I的运行成本;ch0表示单位时间内单件产品的缓存成本;c0表示单位时间下游设备的缺货成本.
本文研究带有缓存区的双机生产系统,针对I可靠度和加工能力均发生衰退的情况,以生产系统长期平均成本最低为目标,需要确定最佳缓冲容量K*,上游设备I置换前达到维护阈值的最优次数M*以及最优维护阈值W*,即寻找最优的设备维护和缓存配置策略(K*,M*,W*).
2 建立模型
2.1 生产系统时间模型
2.1.1缓存积累期 因I加工能力发生退化,第j+1 件产品的加工周期Ti,j+1和第j件产品的加工周期Ti,j之间的关系为
Ti,j+1=Ti,j+ΔTi,j+1
(1)
以额定加工周期与实际加工周期的比值来表示设备的加工能力,同时根据假设条件⑤,在τ时刻将额定加工周期从T0调整至T1,则设备的加工能力A满足:
(2)
式中:∑ΔT和∑ΔT′是τ时刻设备在额定加工周期分别为T0和T1时对应的加工周期增量,可求得加工时间增量之间的关系为
(3)

Ti,j=

(4)
式中:ΔTi,k~Γ(αt,βt),Γ(αt,βt)是设备I在额定加工周期为T0时,加工周期增加量的分布;φi是第i次预防维护的加工能力修复参数.
I完成第1件产品前,P处于缺货状态,因此I完成第j件产品后对应的缓存容量为
(5)

(6)

(7)
2.1.2平稳生产期 I的额定加工周期调整为T0,直至其综合性能状态缓慢退化至阈值W,平稳生产期结束,I停止生产.I在生产第i个周期第j件产品时,可靠度R和加工能力A的综合状态量wi,j为
wi,j=Ri,jAi,j=
(8)

Ti,j=

(9)
式中:ΔTi,k~Γ(αt,βt).
2.1.3缓存消耗期 I进行预防维护或置换时,P以稳定的速度消耗缓存.进入第i个预防维护周期的缓存消耗期后,P将剩余缓存Klast(i)消耗完的时长为
tB(i)=T0Klast(i)+T0(Ni-Klast(i))+
Ti,1-ti=T0Ni+Ti,1-ti
(10)
缓存消耗期系统状态分为2种情况:
(1) 预防维护或者置换结束时,缓存已经消耗完毕,即当i (11) (2) 若预防维护或置换结束时,缓存仍未消耗完毕,即当i (12) 根据式(10)~(12),可以求得I从投入使用到置换的总时间: (13) 2.2.1设备维护成本 在生产实际中,预防维护后故障率会显著降低,但仍劣于初始状态,同时故障率上升的速度变快[8-9],因此本文将役龄递减因子ai[10-11]和故障率递增因子bi[12-15]相结合,建立混合故障率模型,描述设备可靠度修复结果.预防维护前后,设备故障率函数之间的关系为 λi+1(t)=biλi(t+aiti) 假设设备加工某件产品的过程中,可靠度以及加工能力保持不变,并且设备的失效率服从双参数Weibull分布,则I生产第j件产品过程中的故障率为 λi,j= (14) CM=Cpm+Ccm= (15) 2.2.2缓存成本和缺货成本 由图2可见,不同的生产阶段中缓存变化的状态大有不同.因此,在计算缓存成本时,对3个阶段分别进行讨论.另外,缓存数量与下游设备是否缺货直接相关,故将缓存成本和缺货成本一并分析. (1) 缓存积累期.此期间缓存量逐渐增加,直至到达设定的缓存容量上限K.在第i个预防维护周期的缓存积累期,至第j件产品生产完成时刻,P的累积产量为 (16) 求解I在缓存积累期内生产第j件产品过程中产生的缓存成本,需考虑缓存数量是否改变,即P累积产量是否增加,因此缓存成本为 CH1(i,j)= (17) 根据式(16)~(17)可以计算第i个维护周期中缓存积累期产生的总缓存成本: (18) 在缓存积累期,P仅在I加工第1件产品时发生缺货,因此P的缺货成本为 CS1(i)=c0Ti,1 (19) (2) 平稳生产期.随着I加工能力的下降,I对缓存区的供给速度将逐渐低于P对缓存区的消耗速度,缓存区在制品容量减少.I在第i个维护周期平稳生产期内生产第j件产品的过程中,实际缓存数量与K的最大差值为 (20) 若ΔK(i,j)≤K,说明直至第j件产品生产完成,即使I的加工能力有退化,缓存量仍能保证P的正常生产,不发生缺货.为了降低不必要的建模复杂度,默认I加工单件产品的实际周期Ti,j不超过系统额定周期T0的2倍,即Ti,j≤2T0.考虑缓存数量可能改变,由此求得平稳生产期第j件产品生产过程中产生的缓存成本: CH2(i,j)= (21) 接下来,根据平稳生产期结束时P是否发生缺货,本文分情况进行了讨论. 情况1若缓存充分,下游设备始终未发生缺货,根据式(20),I加工能力下降造成的缓存量下降的最大值为 (22) 在第i个维护周期的平稳生产期结束后,缓存数量为Klast(i)=K-ΔKi,此种情形下,缓存成本为 (23) 第i个维护周期的平稳生产期不发生缺货,因此有 CS2(i)=0 (24) (25) 该情况产生缺货成本,且I在加工第Ni件产品之后,其可靠度和加工能力的综合性能状态首次达到设定的预防维护阈值,即wi,Ni≤W,相应期间内总的缺货成本为 (26) (3) 缓存消耗期.第i个维护周期的缓存消耗期开始时生产系统的缓存量为Klast(i),系统进入该阶段后,P将剩余缓存全部加工完毕需要的时间为tB(i). 若Klast(i)=0,即系统在预防维护或置换开始时,缓存已经消耗完毕,则该阶段不产生缓存成本: CH3(i)=0 (27) 对应的缺货成本为 (28) 若Klast(i)>0,缓存消耗期内产生的缓存成本为 (29) 在Klast(i)>0的情形下,无法确定是先完成预防维护或置换动作,还是P先加工完剩余缓存量,因此该阶段缺货成本为 CS3(i)= (30) I在综合性能状态第M次退化到达设定的阈值时进行置换,再综合上文中各阶段各项成本,可以计算在I的寿命周期内,该生产系统总缓存成本和总缺货成本为 CH+CS= (31) 2.2.3设备运行成本 评价本文描述的双机系统时,P始终正常运行,因此仅考虑I的运行成本.根据式(4)和(9)对加工时间的定义,可以计算第i个预防维护周期的运行成本为 (32) 因此,在I的寿命周期内,总的运行成本为 (33) 系统总成本包括I的维护成本CM、更换成本CR、运行成本Cop、在制品缓存成本CH和下游设备的缺货成本CS,I的寿命周期为Ttotal,从而可计算出系统的平均总成本为 (34) 以平均总成本为目标函数,对设备维护与置换策略和缓存容量设计进行联合决策.通过最小化求解式(34)中的Cavg,确定最优策略(K*,M*,W*). 求解前,考虑实际情况确定缓存区的最大允许量Kmax,并根据现有的设备相关资料确定设备维护次数上限Mmax,同时设定决策变量W的优化范围为[W1W2],其中W1 (2)K=1,M=1,W=W1; (4)W=W+0.01,若W≤W2,返回 (3);否则转(5); (5) 令K=K+1,W=W1,若K≤Kmax,则转(3),否则转(6); (6) 令M=M+1,K=1,W=W1,若M≤Mmax,则转(3),否则程序结束. 根据生产实际及文献[2]内容,本文选取参数进行数值分析,如表1所示. 根据第3节的求解流程,列部分计算结果于表2中. 表1 参数取值 表2 不同缓存容量下最优预防维护策略及相应平均成本 本文研究的一个关键点为缓存对整个生产系统带来的影响,缓存一方面有效降低了I维护及退化所导致的P缺货的风险,另一方面其自身又将产生不可忽视的花费.因此,为了凸显本文策略的有效性,在相同假设条件下,比较设置缓存和不设置缓存两种情况下系统的长期运行成本.当不设置缓存时,I的额定加工周期不变,与P一致.通过类似的求解流程,可得到联合决策的最优解为(M*=3,W*=0.2),相应的平均成本则高达 11.697 4 美元. 对比2种模型处于最优解时的各项成本,表3中数值均为系统在I寿命周期内的各项平均成本.从对比数据可以看出,设置缓存产生的相应成本远远小于不设置缓存导致的缺货成本.考虑到总成本的差异主要来自于缓存成本和缺货成本之间的差距,因此本文进一步讨论了当单位时间缺货成本与单位时间缓存成本的比值变化时,设置合理缓存是否仍具有经济上的优越性.如图3所示,保持ch0不变,c0/ch0取值为10,50,100,200,300,400,500.比较总成本,当c0/ch0增大即缺货成本增加时,设置缓存带来的成本节省愈发明显;只有在该比值小至10时,有缓存和没有缓存这两种策略的总成本接近,但是考虑到文本所研究系统在实际中的应用场景,下游设备(如汽车总装的下游装配线)缺货的成本显著高于缓存成本,因此c0/ch0的值应远大于10.再观察图3中缺货成本和缓存成本的对比,随着c0/ch0增长,缺货成本的增长明显,但缓存成本的增长速率明显变缓至维持在一定水平,这也解释了缺货成本愈高,设置缓存愈加经济的原因.综上,合理的缓存有利于生产系统的长期运营,联合决策设备预防维护策略和缓存配置是正确的选择. 表3 各项平均成本对比 图3 成本随c0/ch0变化的分析 本文基于设备可靠度和加工能力退化的规律,将考虑设备综合性能退化的预防维护策略引入带有缓存区的双机系统中,对生产过程进行了细致描述.依据缓存区的状态变化,本文将生产过程分为3个阶段,即缓存积累期、平稳生产期和缓存消耗期,并分别对各阶段缓存数量的变化建立模型.通过计算各阶段内产生的缓存、缺货、维护及运行成本,建立了以上游设备寿命周期内平均成本最低为目标,优化设备预防维护策略和缓存配置的联合决策模型.算例分析结果表明,尽管缓存将产生部分花费,合理设置缓存仍能够有效减少总成本. 实际生产中,3台及以上设备构成的生产线普遍存在,且需考虑设备间的串并联关系,因此未来工作中将进一步研究复杂多机系统的缓存配置问题.


2.2 生产系统成本模型









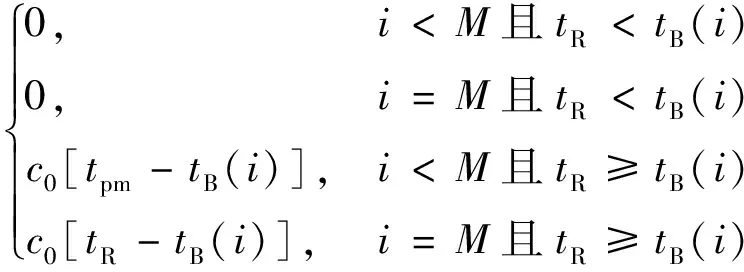


3 求解方法
3.1 求解目标
3.2 求解过程

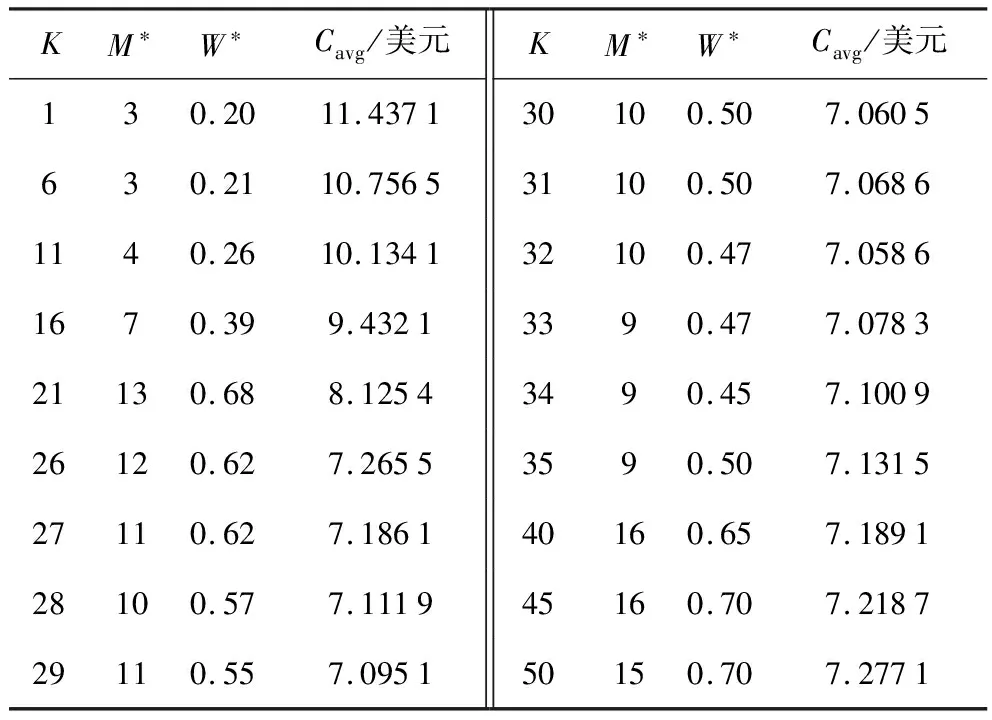
4 算例分析及讨论




5 结语

