曲线相切问题初探

☉江苏省张家港市高级中学 张新秀

一、提出问题

（1）求椭圆的方程.

（2）椭圆上是否存在点P（x，y）到定点A（t，0）（其中0＜t＜3）的距离的最小值为1？若存在，求出t的值及点P的坐标；若不存在，请说明理由.

解：（1）设椭圆的方程为mx2+ny2=1（m＞0，n＞0，且m≠n），将点M、N的坐标代入，解得，从而椭圆的方程为

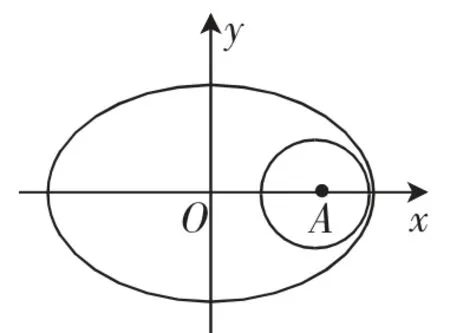
图1 t=2时

但课后，有位同学问了笔者一个问题：老师，您用函数最值法来解这道题，我想“以A为圆心，1为半径的圆与已知椭圆相切”是不是确定t的值更简单呢？如果行，那又为什么得到，与您的结果不同呢？

二、教学反思

针对这一问题，笔者进行了思考，又与办公室里的同行进行了讨论，结果也是意见不一致，故而将问题作了梳理，有了以下几点思考：

（1）直线与圆锥曲线的位置关系，特别地，直线与圆、椭圆的位置关系用直线方程与曲线方程的联立方程组的解的个数来判断，用判别式也是方法之一；因为直线与圆的位置关系，可以通过弦心距与半径相比较来判断，但椭圆因为“椭”的原因，只能通过方程组消元后的一元二次方程的判别式来判断.在高中阶段最重要的内容是直线与曲线的相切问题，这里强调的是线——切线.而两条曲线的“相切”本来是高等数学中涉及的内容，所以学生及教师将直线与曲线相切的解决方法直接用于解决两条曲线相切的问题，显然是要出问题的.

（2）虽然两圆相切（包括内切与外切）是指两个圆有一个公共点时的位置关系，但不能认为解决两条曲线的相切问题也相当于判别式为0就等价于两条曲线相切了.

（3）事实上，若考虑以A为圆心、1为半径的圆与椭圆相切，即将，消去y后，整理得5x2-18tx+9（t2+3）=0（※），由Δ=0，结合条件0＜t＜3，得，而此时方程（※）有且只有唯一的解，而，即，所以原方程组无实数解，这说明椭圆与圆没有交点（如图2所示）.

图2 时

（5）而在高等数学中，两条曲线相切，通俗地讲，就是两条曲线只有一个交点，而且在该交点有一条共同的切线.那么，本题中椭圆与圆（x-2）2+y2=1在点（3，0）处是相切的.

（6）由椭圆与圆联立的方程组的解的问题，不等价于消元后所得的一元二次方程的解（用判别式），这是因为还要考虑到椭圆的范围问题，即x、y的取值范围所限.如（※）中虽然Δ=0，但椭圆与圆却没有交点；（※※）中Δ＞0，方程虽有两个解，但椭圆与圆却只有一个交点.

解：①设P（x，y）因为x∈［-3，3］，0＜t＜3，所以若，即时，则当x=取得最小值；若以A（t，0）为圆心，为半径画圆，则此时圆与椭圆相切，切点坐标为，此时Δ=0，但PA的最小值，不等于1，即当时，椭圆上到点A（t，0）的距离的最小值为1的点不存在.

综上所述，椭圆上存在点P到定点A的距离的最小值为1，点P的坐标为（3，0），A（2，0）.即参数t的值为2，而不是

三、教学运用

但是由于同学受直线与二次曲线位置关系的判定法则这一思维定式的影响，往往只考虑消元后所得的二次方程的判别式而忽略了方程组解的整体情形.在平时的教学中，笔者思考并总结了解决这类问题的“双判别式法”，收到了较好的复习效果，在判断二次曲线的交点问题时，必须对消元后所得关于变量x和关于变量y的两个方程的判别式同时进行讨论，方可得出合乎逻辑的正确结论.

例1在抛物线y=ax2（a＞0）的上方（y≥ax2），求出一个与抛物线相切于原点的最大圆的方程.

解：圆的方程可设为x2+（y-r）2=r2，①

抛物线方程为y=ax2，②

此题属于两曲线在顶点处有重切点的情形，故须有Δy=0，且Δx=0.

例2已知抛物线C：y=（x+1）2与圆M：（x-1）2+有一个公共点A，且在点A处两曲线的切线为同一直线l.

（Ⅰ）求r；

（Ⅱ）设m、n是异于l且与C及M都相切的两条直线，m、n的交点为D，求D到l的距离.

解：（Ⅰ）设A（x0，（x0+1）2），对y=（x+1）2求导得y′=2（x+1），故l的斜率为k=2（x0+1）；

图3

当x0=1时，不符合题意，所以x0≠1，圆心为，MA的斜率为由l⊥MA，知kk1=-1，即2（x0+1）·，解得x0=0，故A（0，1）

一般地，给定抛物线y2=2px（p＞0），设A（m，0），m＞0，P是抛物线上的一点，且|PA|=d，则当0＜m≤p时，以A为圆心的圆与抛物线切于顶点，顶点到点A的距离最小，但此时Δ≠0；当m＞p时，以A为圆心的圆与抛物线相切时，切点到点A的距离最小，此时Δ=0.

通过对教学所反映的问题进行研究和探索，对教学有了更深刻的感悟.有时是学生教会教师思考，特别是那些看似平常的、浅显的、从未怀疑的问题，要主动进行“非常”的思考，不能将这些问题一直放在“遗忘的角落”，应不断地思考，不断地深入研究，这样才能使教学内容更符合学生的“最近发展区”，才能有效地促进学生数学能力的提高，培养和发展学生的数学应用意识和创新意识，达到以例启思、以点带面、触类旁通的目的，本文抛砖引玉，希望有更多的一线教师通过教学实践，做更进一步的研究.