谈立体几何教学中需要强化的几个关键点

☉江苏省海安市曲塘中学 万海兵

立体几何是高中数学的主干内容，也是考查考生空间想象能力、推理认证能力的有效载体，在教学中我们要对解题思路与方法进行提炼，对解题过程进行规范，注重数学语言的简捷性，锻炼与培养学生良好的解题习惯.

一、强化对知识点的梳理

在教学中要引导学生注重对重要知识点的整理与再加工，对各知识点的脉络有一个清楚的认识，了解这些知识点在整个高中数学的作用与价值，整体把握知识点的内部结构，做到心中有数.

如：空间中的平行关系，主要包括：

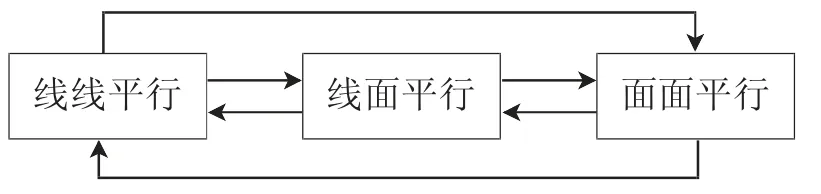
知识的梳理中要熟练掌握三者间的相互关系，如：欲证“线面平行”，既可从“线线平行”入手，也可从“面面平行”入手.

例1如图1，在三棱锥PABC中，D、E、N分别为棱PA、PC、BC的中点，M是线段AD的中点.求证：MN∥平面BDE.

图1

分析1：从面面平行入手，经过MN构造与平面BDE平行的平面.取AB的中点O，连接NO，MO，易证平面MON∥平面BDE，进而问题得证.

分析2：从线线平行入手，连接PN交BE于点F，连接DF，利用三角形重心的性质可证得DF∥MN，进而可证得MN∥平面BDE.

当然，不论哪种思路，都要依赖于线线平行关系.在备考中要注意“线线平行”关系的寻找与利用.

二、强化良好的审题习惯

问题解决的最终目标就是求出结论或说明已给结论的正确或错误.因而解决问题时的思维过程大多都是围绕着结论这个目标进行定向思考的.教师要引导学生通过审题，探索已知条件和结论之间的内在联系和转化规律，善于从条件或结论中捕捉解题信息，并进行转化，从而确定解题方向.

例2如图2，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD.求证：

（1）略；

（2）AD⊥AC.

审题路线图：要证AD⊥AC→需证线面垂直：AD⊥平面ABC→需证线线垂直：AB⊥AD（已知），BC⊥AD（需证）→需证线面垂直：BC⊥平面ABD→靠拢已知：平面ABD⊥平面BCD，平面ABD∩平面BCD=BD.

图2

三、强化常规解题方法的总结

例如：对于三视图问题主要采用还原法，即将所求的几何体还原于特殊的长方体或正方体中.

例3（2018年全国卷）在长方体ABCD-A1B1C1D1中，AB=BC=1，AA1=，则异面直线AD1与DB1所成角的余弦值为______.

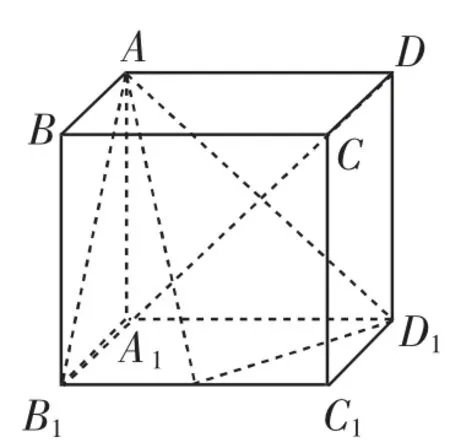
图3

本题的求解既可以利用平移法、补形法来构造线线角，也可以利用向量运算和坐标运算来直接求解.（答案为，过程略）

四、强化规范性解答

在解答立体几何问题时，不规范性的地方主要体现在以下几个方面：

（1）建立空间直角坐标系时，坐标轴两两垂直的关系未证明，就应用.

（2）计算错误，如点的坐标、直线方向向量的表示及法向量的求解.

（3）跳步解答，任何的“跳步”书写都容易产生歧义，都是要失分的.如证明直线l与平面α（m为α内的直线）平行时，要说明

（4）对两条异面直线所成的角、直线与平面所成的角、二面角及空间两向量的夹角范围不明确.

例4如图4，三棱柱ABC-A1B1C1的侧面BCC1B1是平行四边形，BC1⊥C1C，平面A1C1CA⊥平面BCC1B1，且E，F分别是BC，A1B1的中点.

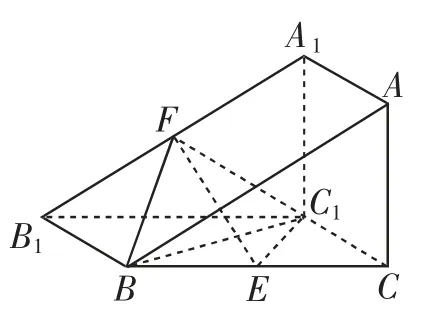
图4

（Ⅰ）求证：EF∥平面A1C1CA.

（Ⅱ）当侧面A1C1CA是正方形，且BC1=C1C时.

（1）求二面角F-BC1-E的大小.

（2）在线段EF上是否存在点P，使得AP⊥EF？若存在，指出点P的位置；若不存在，请说明理由.

解析：（Ⅰ）如图5，取A1C1的中点G，连接FG，GC.在△A1B1C1中，因为F，G分别是A1B1，A1C1的中点，所以FG∥B1C1，且

在平行四边形BCC1B1中，因为E是BC的中点，所以EC∥B1C1，且

所以EC∥FG，且EC=FG.所以四边形FECG是平行四边形.所以FE∥GC.

又因为FE⊄平面A1C1CA，GC⊂平面A1C1CA，所以EF∥平面A1C1CA.

（Ⅱ）因为侧面A1C1CA是正方形，所以A1C1⊥C1C.

又因为平面A1C1CA⊥平面BCC1B1，且平面A1C1CA∩平面BCC1B1=CC1，所以A1C1⊥平面BCC1B1，A1C1⊥C1B.

又因为BC1⊥C1C，所以以C1为原点建立空间直角坐标系C1-xyz，如图6所示.

设C1C=a，则A（0，a，a），B（a，0，0），C（0，a，0），A1（0，0，a），B1（a，-a，0）

（1）设平面FBC1的一个法向量为n=（x，y，z）.

又因为A1C1⊥平面BC1E，所以是平面BC1E的一个法向量.

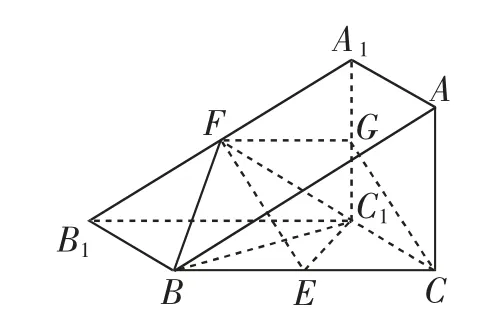
图5

图6

由图6可知，二面角F-BC1-E为钝角，所以二面角FBC1-E的大小为

（2）假设在线段EF上存在点P，使得AP⊥EF.

故点P在点E处时，有AP⊥EF.

总之，在立体几何的教学中除了强化上述四个关键点，解答或证明过程还要做到“步步有理有据”，分清主次，出现错误之后，应尽可能地及时订正，从根源上找到错因所在，及时总结知识上存在的漏洞，真正做到审题到位，下笔准，答题快.