APOS理论视域下“用字母表示数”教学设计

王群

APOS理论是一种建构主义个体学习理论，有学者认为，学生学习数学概念要进行心理建构，此建构过程需经历操作或活动（Action）—过程（Process）—对象（Object）—图式（Schema）等四个阶段。以“用字母表示数”一课为例，经历操作或活动阶段，从游戏情境出发，引导学生关注“用字母表示数”的现实模型，经历提问、操作、计算等活动，从而初步感知概念的本质属性，建立概念表象;过程阶段，运用分析、比较、综合等方法，帮助学生逐步抽象出概念本质;对象阶段，通过简写字母式，将概念逐步压缩为一种心理程序，从而进行符号间的高阶运算;图式阶段，引导学生思考概念间的内在联系，建立必要的模型，将概念内化。

【教学内容】苏教版五上“用字母表示数”例1～例3。

【教学目标】

1. 初步理解用字母可以表示数，会用含有字母的式子表示简单的数量、数量关系和计算公式，初步学会计算含有字母式子的值，了解字母式子的乘法简便写法。

2. 完整地经历用含有字母的式子表示简单的数量、数量关系和计算公式的抽象过程，进一步体会数学的抽象性与概括性，发展符号意识，培养初步的代数思维。

3. 体会数学表达的简洁之美，培养主动思考、回顾、反思的学习习惯。

【教学重点】会用字母表示数和简单的数量关系。

【教学难点】理解字母式表示运算结果和数量关系的双重性。

【教学过程】

一、游戏导入，引入新课

师：同学们用扑克牌玩过24点游戏吗？看谁最先算出24点。（课件出示扑克牌5、2、3、A）

师：奇怪，没有看见1呀？（这里的字母A就表示1）

小结：在扑克牌中，人们用特定的字母表示数。算24点时，A就表示1，字母A在这里表示一个确定的数。（板书：表示确定的数）扑克牌里还有哪些字母也表示确定的数呢？

师：其实，不仅生活中有用字母表示数，研究数学更需要用字母表示数。（板书揭题：用字母表示数）你想到什么问题了吗？带着这些问题，我们一起走进今天的学习。

设计意图：数学概念的形成最初要经历从直观到抽象的活动过程。这正是操作或活动阶段的要义。在该阶段中，操作活动将使学生受到外部刺激。外部刺激主要分为情境和操作方式这两个方面。情境包含生活情境、数学情境等;操作方式不仅包括外在的操作活动，还包括内在的思维活动，如回忆、猜想、判断、计算等。

在本环节中，教师先组织学生计算24点，极大地激发了他们的学习兴趣，将生活经验与数学知识建立链接。待教师揭示课题后，进一步引导学生提问，将他们的真实问题与教学目标进行衔接，使新知学习成为学生的内在需要，从而实现深度学习。

二、自主探究，初步感知

1. 拼摆三角形，为探索用字母表示“变化的数”作铺垫。

师：让我们的研究从用小棒摆三角形开始吧，摆一个三角形需要几根小棒？

师：摆两个三角形呢？你能用算式表示摆小棒的根数吗？

师：摆三个三角形呢？小棒的根数会用算式表示吗？摆四个呢？（课件逐步出现三角形，并依次板书：1个，3根;2个，2×3根;3个，3×3根;4个，4×3根）

设计意图：在活动阶段，个体对接收到的外部刺激进行逐步内化抽象。課件依次呈现三角形的个数，引导学生多次经历观察、思考、计算等直观操作活动。在活动中体会三角形形状不变是源于小棒根数与三角形个数的稳定关系。在多次活动中剥离直观属性，逐步形成小棒的根数与三角形个数关系的思维表象。杜宾斯基认为，数学教学是数学活动的教学，操作运算行为是数学认知的基础性行为。学生要通过实际演算和头脑中的心理操作来获得知识，否则数学概念将成为无源之水，无本之木。

2. 师：在摆的过程中，你发现三角形的个数是变化的，小棒的根数也是变化的，那什么是不变的呢？（围成一个三角形需要3根小棒）

师：如果老师有足够多的小棒，你想摆几个三角形，又需要几根小棒呢？你想摆几个？一直摆下去，能摆得完吗？摆不完怎么办呢？（板书：省略号）先想一想，再和你的同桌轻声交流。

预设回答：用字母a表示三角形的个数，小棒的根数就是a×3。

师：a和a×3分别表示什么意思呢？当三角形的个数用a表示时，小棒的根数为什么可以用a×3来表示呢？

小结：和算24点中的字母A不同，这里的a可以表示所有的自然数，a表示的不再是一个确定的数，而是一个变化的数。（板书：变化的数）

3. 师：用n来表示三角形个数可以吗？这时小棒的根数又可以怎样表示？指出：同一个数还可以用不同的字母来表示。

设计意图：当用小棒摆三角形的活动多次重复，被学生熟悉之后，操作活动就可以内化为心理操作，由此进入概念学习的过程阶段。学生可以自如地在大脑中实施“摆小棒”的过程。通过让学生自由说“想摆几个三角形，需要几根小棒”，学生会发现三角形越摆越多，而且怎么摆也摆不完，自然引发学生对规律的探索和发现。再通过独立思考、小组交流等教学策略，学生体会用字母式既表示变化的数又表示数量关系的双重性。

三、游戏引领，提升感知

1. 在游戏中感受用字母表示相差关系的量。

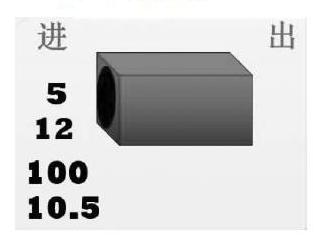
体验字母式的形成过程，数学游戏——神奇魔盒。

师：接下来，老师想和大家一起来玩一个小魔术。这里有一个神奇的魔法盒子，它的神奇在于，左边进入一个数，穿过盒子之后，它就会变成另外一个数。

课件演示：输入5，输出15;输入12，输出22;输入100，输出110。

师：是否有人已经发现了什么？（输入的数进入盒子出来之后就增加了10）

验证猜想：输入10.5，输出20.5。

2. 尝试概括，揭示本质。