多项式插值算法处理GNSS精密钟差数据适应性研究*
曹可劲 马恒超 朱银兵 李 豹
(海军工程大学电气工程学院 武汉 430033)
1 引言
定位数据的后处理中,对精密钟差产品进行插值计算是初始步骤,最常采用的是拉格朗日、牛顿和切比雪夫多项式插值法。目前IGS分析中心提供的最终产品,钟差精度为0.1ns,优于广播星历约2个数量级[1,11],折算成等效卫星测距误差SISRE已下降到厘米级,鉴于多项式插值固有的特性,在此精度上进行插值计算应仔细处理。例如文献[2]对北斗三种卫星轨道坐标采用了拉格朗日和牛顿插值法分别进行了计算,认为应该根据不同情况选择不同阶数;文献[3]对拉格朗日、牛顿、滑动拉格朗日三种插值方式进行了对比分析,认为对于钟差插值线性插值与多项式插值的精度差别不大;文献[4]认为切比雪夫插值法精度比拉格朗日插值法高,但阶数高了受影响比较大,精度变化比较剧烈。以上分析基于各种多项式插值的特点,但都没有给出IGS数据插值处理的一般原则,本文选择最具代表性的滑动拉格朗日插值法进行分析,找出基本规律和选择的策略。
2 问题描述
下载IGS某天的30s、5min间隔的精密钟差产品,以及5min和15min的精密星历产品,分别做两点间一阶线性插值和多阶滑动拉格朗日插值[4]:将5min间隔的精密钟差数据内插生成30s间隔的数据,将15min间隔的数据内插生成5min间隔的数据。将内插得到的值与原始30s间隔的精密钟差数据进行对比,分析内插精度。其中拉格朗日内插时,5min间隔内插成30s间隔采用通常的10阶运算,15min间隔内插成5min间隔采用8阶运算,取30个点进行评估。内插精度用误差绝对值的平均值表示,结果如图1、图2所示。
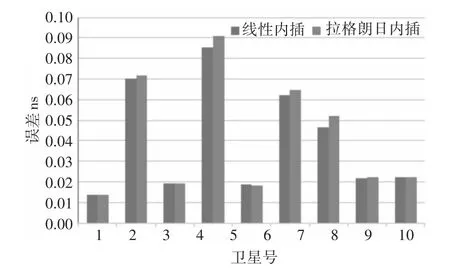
图1 5min内插到30秒精度比较

图2 15min内插到5min精度比较
从以上计算发现,两种插值过程中除个别卫星,绝大部分拉格朗日插值的精度都比直接线性插值精度低,我们对其它日期的数据进行计算,发现该现象普遍存在。
3 问题分析
3.1 时钟漂移特征
目前导航卫星搭载有三种类型的原子钟:铷钟、氢钟和铯钟。从长期稳定性而言,三种类型的钟是逐步提高的,但铷原子钟在质量、体积、功耗等方面占有优势,氢钟在短期和中期稳定度指标方面占有优势,铯钟的准确度和漂移率指标综合指标最好[5,12]。因此美国GPS采用了铯原子钟和铷原子钟结合的方式,欧盟的伽利略、俄罗斯的三代格洛纳斯以及我国正在建设的北斗三号,采用铷原子钟和被动型氢原子钟相结合的方式[6]。
相对于轨道误差,采用不同的原子钟和搭配方式,卫星的时钟误差变化规律要复杂得多。为了普通用户使用方便,广播星历中将时钟漂移简化为二次曲线规律,时钟模型采用了一个2小时更新的简单二阶线性函数表示[7]:
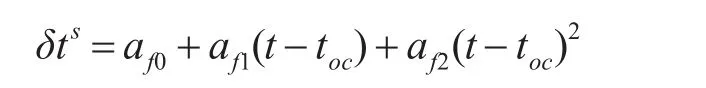
其中系数af0、af1、af2以及参考时间toc随着卫星导航电文更新。由于该模型主要考虑的卫星钟差十分钟级到小时级的变化特性,因此对时间参数t的敏感性很弱,造成时钟预报误差只能到纳秒以上的精度。
3.2 精密钟差数据特征
IGS提供的精密钟差产品分为两种格式:一种是以5min和30s间隔由单独的时钟文件给出,另一种以5min和15min间隔包含在精密星历文件中给出。对比广播星历的时钟漂移模型,将各精密时钟数据画成曲线,直观考察变化规律。任意取2016年9月3日凌晨开始的15min间隔、5min间隔和30s间隔的数据分别进行分类,可以得到三种情况:
类型一:三种数据间隔的线性都比较好,且趋势相同,如图3所示。
类型二:随着数据间隔减少,线性度下降,尤其30s间隔数据情况恶劣,如图4所示。
类型三:所有间隔的数据都不呈线性,且趋势不同,如图5所示。
从分析的数据来看,随着间隔缩小,钟差线性度变差,相对抖动加大。从分析的数据观察,绝大部分钟差数据都属于后两种情况。

图3 9号卫星钟差曲线
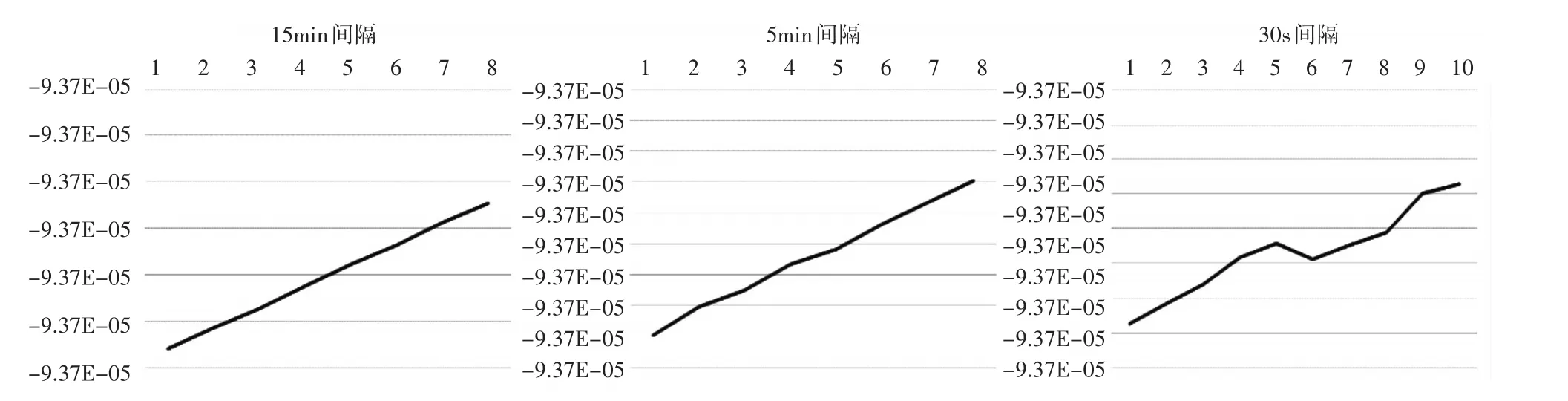
图4 5号卫星钟差曲线

图5 8号卫星钟差曲线
3.3 多项式插值模型的适用性
各类多项式插值方法要保证精度,需要测量值符合某个函数的变化规律[8],插值中所构造的插值函数应该尽可能逼近该函数。以典型的拉格朗日插值法为例,在给定的k+1个样本点:(x0,y0),…,(xk,yk)基础上构造一个阶数为n的多项式lk(x),其中xj对应着自变量的位置,而yj对应着函数在这个位置的取值。假设任意两个不同的xj都互不相同,那么拉格朗日插值多项式为
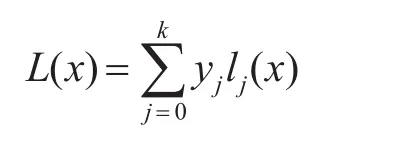
其中每个lk(x)为拉格朗日基本多项式(或称为插值基函数),其表达式为
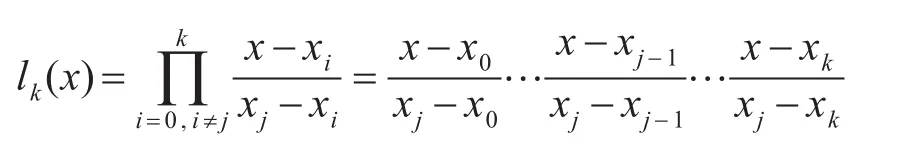
该多项式的特点是在xj上取值为1,在其它点上取值为0。由式中可知,拉格朗日插值曲线可以精确无误地通过已知样本点,同时保证了插值点也是线性连续的。虽然通常来说,拉格朗日插值多项式的阶数越高,插值函数越精确,但在实际中容易造成数值剧烈变化,即所谓的“龙格现象”[9],反而降低了插值精度。
对比上一节中的时钟漂移特性曲线,这种以多项式拟合时钟误差曲线的方式,在小尺度间隔情况下,并不能准确代表导航卫星时钟漂移特性,即相对于分钟以上时间粒度,秒级间隔呈现的时钟漂移随机误差,不能用分钟级间隔的样本数据等效表示。
4 插值模型选择策略
4.1 数据预分析
首先对用于插值的样本数据进行线性度分析,采用最小二乘构建标准线性曲线,对于给定样本点 (xi,yi),i=1,2,…,N,存在Q≥ 0,求一次函数y=a+bx,使总误差:

即参数a,b应满足此时
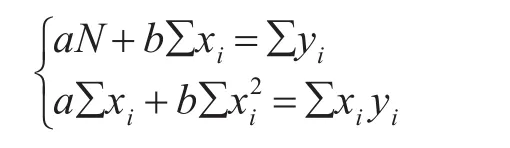
以得到的Q值作为参考,本文以每颗星10个连续样本值计算Q值。
4.2 仿真计算
1)取2016年9月4日00时00分至24时00分的5分钟间隔的GPS精密钟差数据计算分析。计算各卫星的Q值,如图6所示,并分别用一阶线性相邻内插法、多阶滑动拉格朗日插值法得到30s间隔的钟差数据,以已知30s间隔精密钟差数据为参考值,计算各星钟差随时间变化的误差情况,其中1阶线性插值误差和9阶滑动拉格朗日插值误差如图7、8所示。文中使用的滑动拉格朗日插值法,只采用原样本点中部的插值结果,该区间相对其他样本点区间精度较高[10],如使用9阶,需10个样本值,采用第5和6样本值间的插值。
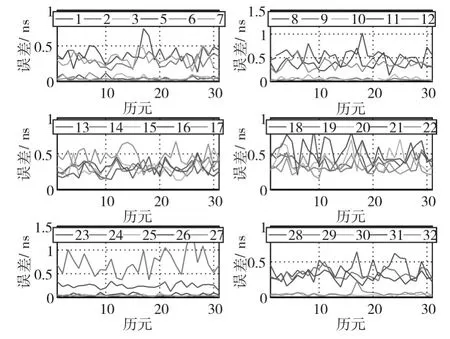
图6 各GPS卫星钟差的Q值

图7 1阶线性相邻内插后钟差的误差
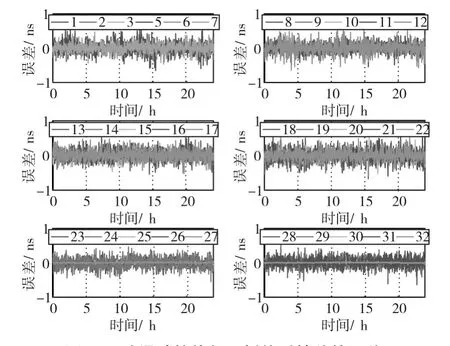
图8 9阶滑动拉格朗日插值后钟差的误差
2)Q值与各插值法精度的关系
根据1)中图示,每颗星Q值及误差均随时间变化,计算各星Q值的平均值,可将所有GPS卫星分为三组,如表1所示。

表1 GPS卫星钟差的分类情况
选择9号、5号、8号星为各类型代表,比较线性插值与不同阶滑动拉格朗日插值情况,其插值精度如表2所示。

表2 三种分类的插值计算误差对比
从计算结果比较,类型一对应的卫星插值精度最好,随着真值数据的线性程度下降,拉格朗日插值模型的计算误差相对于线性插值模型先增大后减小,线性插值精度整体优于拉格朗日插值;对表中各卫星而言,随着滑动拉格朗日插值阶数提高,误差逐渐增大。对其他更多数据进行计算,总体上呈现了该特点。
5 结语
拉格朗日算法在实际应用于IGS卫星时钟改正数插值计算时,只有在真值数据线性度较好(Q值较小)时,才可能提高插值的灵敏度,而且要选择合适的阶数,不宜取得过高。随着导航卫星原子钟技术的精度和稳定性提升,目前IGS测量得到的卫星时钟漂移越来越呈现线性特性,尤其时间在分钟以上间隔时更是如此。而且,目前IGS提供的卫星时钟改正数精度已经在十分位纳秒等级[7~8],无论采用哪种插值算法,精度都可以达到千分位纳秒等级,对定位精度的影响区别很小。鉴于拉格朗日算法的计算复杂性,以及存在误差放大的风险,在进行高精度定位时,采用最简单的线性插值反而更可靠。

