重力插值重构前沿与进展

王 彤

（中国空间技术研究院，北京 100094）

0 引言

潜艇在水下执行情报搜集、军事打击以及潜伏等任务时，必须要保证它的隐蔽性和导航定位的准确性，这样才能满足潜艇对水下安全航行及精确打击的需求。惯性导航系统具有自主、高精度、高隐蔽性以及不易受到外界信息干扰等优点，因此潜艇主要依靠惯性导航系统在水下航行。但是惯性导航系统存在系统误差，并且该误差随时间的累积而增大，这就会降低潜艇在水下运行时的精度。针对惯性导航系统存在的不足之处，许多学者提出潜艇在水下航行时，需要修正潜艇惯性导航系统的累积误差；将重力信息与惯性导航系统联合起来的无源辅助导航系统可以对惯性导航的累积误差进行校正，它是目前国际研究的热点。重力匹配导航系统不需要水下潜器浮出或接近水面，测量时也不会向外辐射能量，因此有望实现水下潜器连续长航时精确、自主定位。

1 重力匹配导航系统原理

重力匹配导航系统指的是潜艇通过自身搭载的重力仪来获得潜艇目前位置重力场的特征信息，将获得的实测重力值与海洋重力基准图进行匹配，按照合适的匹配算法最终确定潜艇所在的位置。海洋重力基准图是重力匹配导航的重要组成部分，因此，构建全球高精度和高空间分辨率的海洋重力基准图是非常必要的。船载重力测量、航空重力测量以及卫星重力/测高反演是获取全球海洋重力场的主要技术途径，全球高精度和高空间分辨率的海洋重力基准图能有效提高水下重力匹配导航的精度；然而目前全球海洋重力基准图的质量较低（精度为3 mGal～8 mGal，空间分辨率为1′×1′），因此需要对其进行一定程度的插值加密，将其重构为高精度和高空间分辨率的海洋重力基准图。

2 海洋重力异常图插值方法

目前常见的重力场插值方法有距离加权反比插值法、径向基函数插值法、样条函数插值法、克里金插值法以及改进的Shepard插值法。

2.1 距离加权反比插值法

距离加权反比插值法是最简单的插值方法，该方法根据未知点到已知点距离的加权平均值来计算未知点的值。距离加权反比插值法的具体计算如公式（1）所示[1]。

式中：G0为预测点的重力值；Gi为第i个已知点的重力值；hi为第i个已知点到预测点的距离；μ为指数参数。

2.2 径向基函数插值法

径向基函数（Radial Basis Function， RBF）插值法能够应用于各个领域，例如全球地形、水文、地球物理科学和图像重建，其原理是将已知点作为位置中心，求解得出插值函数的系数，从而获得预测点的值，径向基函数插值法的插值函数的表达式如公式（2）所示[2]。

2.3 样条函数插值法

样条函数插值法是由工程制图中的样条绘图工具发展而来的，一般指的是三次样条函数插值法（Cubic spline function interpolation）。三次样条函数插值法是由几段三次多项式拼合而成的曲线，如公式（3）所示[3]。

式中：Si（x）为三次样条函数；ai、bi、ci和di为待求系数。

2.4 克里金插值法

克里金插值法（Kriging）主要采用地质学中的统计理论和插值方法，以变异函数为插值基础和基本工具，选择合适的变异函数，从而对空间结构和参数进行最优线性无偏估计。克里金插值法分为以下5步：1） 重力场数据的预处理。2）x和y2个方向的实验方差图。3） 拟合最优变异函数计算变异函数（半方差函数）的系数。4） 克里金交叉验证。5） 未知点的克里金估计值。变异函数描述了各个点的空间关系，其表达式如公式（4）所示[4]。

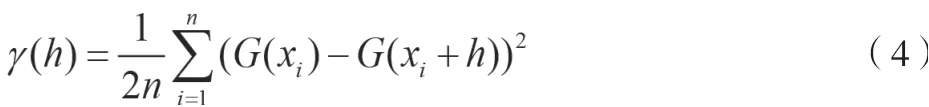
式中：h为点xi到点xi+h之间的距离；n为已知点的总数；G（xi）为点xi的重力值；γ（h）为变异函数。

2.5 改进的二次曲面Shepard插值法

改进的二次曲面Shepard（Modified Quadratic Shepard， MQS）插值法可用于对大规模散乱数据的插值拟合，与距离加权反比插值法相似。改进的二次曲面插值法对领域内外进行主要区分，对进入领域的点进行二次曲面加权运算，领域外的权系数为0，不进行运算。二次曲面函数如公式（5）所示[5]。式中：xi、yi为第i个点的经纬度坐标；ai1、ai2、ai3、ai4和ai5为二次曲面函数的待求系数；Gi为第i个点的重力值；Qi（x）为二次曲面函数。

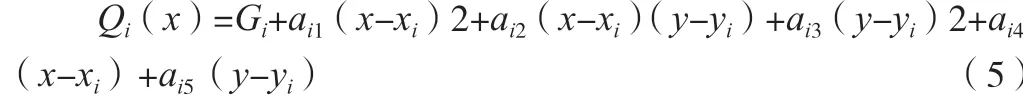
可以通过最小二乘逼近法对已知点的重力值进行拟合求出。

该文对上述5种方法进行深入分析，根据插值、精度计算复杂度、计算时间以及适用范围等评价指标对常见的插值方法进行统计，各个方法的优缺点见表1。

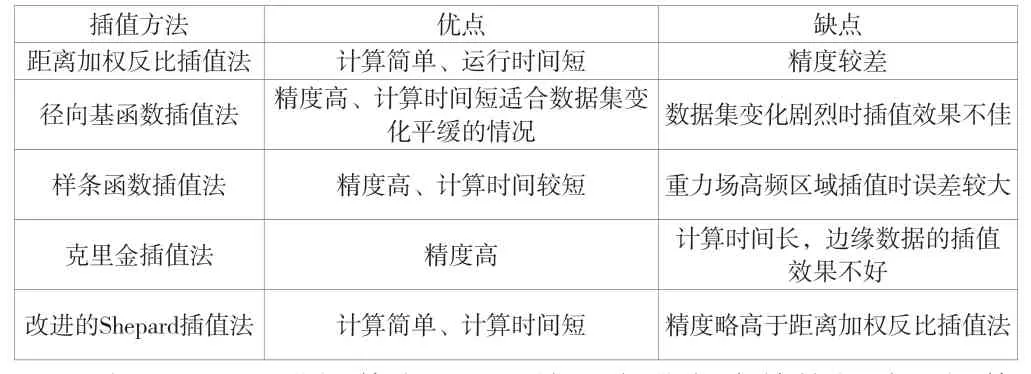
表1 插值法的优缺点对比分析

除了上述5种插值方法，目前很多学者将其他领域的插值方法也应用到重力场插值的过程中，提出了一些改进的插值方法，例如广义抽样扩展插值法、双三次孔斯曲面插值法、不等权最小二乘预测插值和窗口移除恢复技术—克里金插值法等，这些方法的插值精度较高，能有效提高重力场的空间分辨率。

3 团队研究进展

研究团队从事航天、导航、测绘以及海洋等交叉学科的前沿探索与军事应用，对卫星重力学、卫星测高学以及水下导航学开展研究，构建了全球高精度和高空间分辨率的海洋重力基准图，进而为实现自主、隐蔽和高精度的全球水下导航提供了理论和方法支持。该文将上述5种传统插值法进行实验验证和对比分析，选取我国南海区域（东经115°E～116°E、北纬20°N～21°N）的格网化海洋重力异常数据作为实验数据（空间分辨率为1′×1′），如图1所示。

图1（a）和图1（b）分别表示研究区域空间分辨率为1′×1′的二维和三维海洋重力异常图。该区域内海洋异常变化范围较大，因此不同插值方法的误差变化也较大。首先，将空间分辨率为1′×1′的实验数据稀疏为4′×4′；其次，分别用距离加权反比插值法、径向基函数插值法、样条函数插值法、克里金插值法和改进的Shepard插值法将空间分辨率为4′×4′的海洋重力异常插值为空间分辨率为1′×1′的海洋重力异常；最后，求得与原始1′×1′的海洋重力异常的误差，如图2所示。图2为用这5种方法对我国南海区域插值后的误差散点图，可以看出克里金插值法误差分布较为集中，误差最小。插值重构时，为了与原始图片对比，分析插值后海洋重力异常误差的大小，在判断插值方法精度时，一般选用平均误差（Mean error， ME）和均方根误差（Root mean square error， RMSE）作为评价指标，计算公式如公式（6）所示[6]。

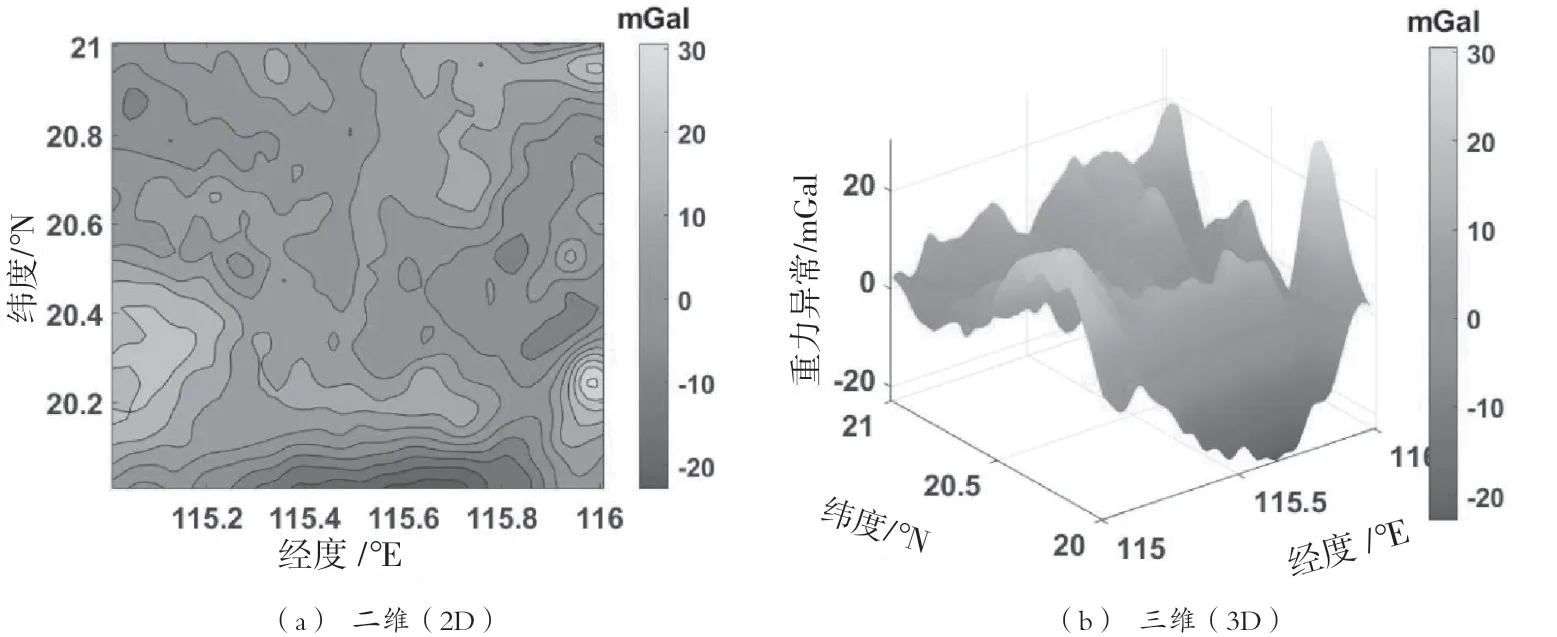
图1 分辨率为1′×1′的海洋重力异常图

图2的统计结果见表2。根据表2可知，与其他4种插值方法相比，距离加权反比插值法的误差较大，其平均误差为1.07×10-1mGal，均方根误差为2.96 mGal，对应图2（a）误差的变化范围较大，误差点分布离散。因此，距离加权反比插值法的插值精度较低，插值效果不好。克里金插值法精度最高，平均误差为3.16×10-2mGal，均方根误差为1.113 mGal，其误差较小，插值效果较佳，适用于对海洋重力场的插值重构。

表2 5种插值方法对我国南海区域插值误差统计

4 结语

重力匹配导航是1种自主无源的导航方式，对潜艇的水下航行具有极其重要的意义。海洋重力基准图对重力匹配导航精度具有一定的影响。该文对目前常见的重力场插值方法的拟合过程进行研究，通过分析对现有的距离加权反比插值法、径向基函数插值法、样条函数插值法、克里金插值法和改进的Shepard插值法进行对比，体现出克里金插值法和样条函数数插值法对海洋重力异常插值重构的可行性，也为未来构建全球海洋重力场基准图提供了可行性建议。

图2 不同方法插值后误差散点图