基于证据理论和直觉模糊集的作战方案评价方法*

王 亮

（1.91776部队 北京 100161）（2.复杂舰船系统仿真重点实验室 北京 100161）

1 引言

作战方案是对作战进程和战法的设想，是军队在筹划作战时最主要的指挥文书，是指挥员决心意志和谋略水平的集中体现。通常在参谋长主持下，以作战部门为主，有关部门参加共同拟制数个作战方案，并选定基本方案。根据情况组织论证、计算机模拟或者沙盘推演，条件允许时还可以进行实兵演练，对作战方案加以检验、修正和完善［1～2]。除此之外还可以建立评价指标体系，利用各种数学解析法，对作战方案进行评价［3～5]。当一些作战方案具有信息高度模糊和不确定的特点时，便无法利用推演、模拟等传统方法进行有效评价，一般的数学解析法的评价效果也不理想，为此，本文利用群决策思想，提出一种基于证据理论和直觉模糊集的评价方法，用于解决此类问题。

2 基本概念

2.1 证据理论基本概念

现有某一作战方案评价的问题，我们能认识到的该方案所有评价结果用集合Θ表示，Θ中所有元素两两互斥，则称集合Θ为识别框架，识别框架Θ中的任意子集都与一个问题答案的命题相对应。

设Θ为识别框架，如果集函数mass：2Θ→[0，1]满足：

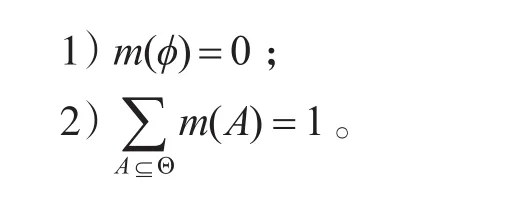
称m为识别框架Θ上的基本可信度分配函数。 ∀A⊆Θ，称m(A)为A的基本可信度，m(A)反映了证据支持命题A的程度，2Θ为Θ的幂集。只要m(A)＞0，则A称为焦元。

设m1和m2分别是同一识别框架Θ上的基本可信度分配函数，那么这两批证据就可以合成，称之为Dempster合成规则。

K是表示证据间完全冲突量的一种度量。

设Θ为识别框架，函数Bel是一个从集合2Θ到［0，1]的 映 射 ，若A⊆Θ ，且 满 足

则Bel(A)称为A的信度函数，表示证据对A为真的信任程度，Bel(Aˉ)表示的是证据对Aˉ为真的信任程度，Pl(A)表示的是证据对A为非假的信任程度。

对于证据理论其他基本理论和基本运算规则请参考相关文献［6～7]，不再赘述。

2.2 直觉模糊集基本概念

直觉模糊集（Intuitionistic Fuzzy Set，IFS）是由保加利亚学者Atanassov在1986年提出的，也是迄今为止对Zadeh模糊集理论最有影响的一种发展和扩充。Zadeh模糊集理论将传统“非此即彼”的明确概念拓展为隶属度可以取［0，1]之间任意值的模糊概念；而直觉模糊集将Zadeh模糊集进一步发展，除了传统的隶属度概念，还提出了非隶属度函数这个新的概念，并由此衍生出犹豫度的概念。因此，相比传统的模糊集理论，直觉模糊集对不确定信息的描述及处理更加全面、灵活。

设X是一个给定论域，定义A为该论域上的一个直觉模糊集

其中μA(x):X→[0，1]和νA(x):X→[0，1]分别代表A的隶属函数μA(x)和非隶属函数νA(x)，且对于A上的所有x∈X，均有0≤μA(x)+νA(x)≤1成立。

直觉模糊集可以简记为A=＜x，μA，νA＞ 或A=＜μA，νA＞/x。不难看出，普通的Zadeh模糊子集对应直觉模糊集A={＜x，μA(x)，1-μA(x)＞|x∈X}。

设X是一个给定论域，对于其中的每一个模糊子集，称πA(x)为A中x的直觉指数，也称之为犹豫度，它是对描述除了“隶属”和“非隶属”之外的不能确定的犹豫程度的一种度量。

对于直觉模糊集其他基本理论和基本运算规则请参考相关文献［8～9]，不再赘述。

3 基于证据理论和直觉模糊集的群决策方法

3.1 可信度函数的直觉模糊集表示

直觉模糊集中的论域X是无指定对象元素的集合，而证据理论中的识别框架Θ同样是从无指定对象元素的集合，因此从集合论的角度分析，两者具有等价性。正因为如此，证据理论中的识别框架Θ中的任一命题A均可看作是论域X上的模糊集合，那么其信度函数Bel（A）是一种模糊测度［10～11]，并且表示∀θ∈A的隶属程度，同样Bel(Aˉ)也是一种模糊测度，进一步可以看出Bel(A)的含义与直觉模糊集中的隶属度函数意义是一致的，Bel(Aˉ)与非隶属度函数意义是一致的。因此，证据理论中的信度函数可以用直觉模糊集的形式表示。

假设某一问题的识别框架为 Θ={θ1，θ2，…θn}，那么对∀θ∈Θ，Θ上的任意命题A可以直觉模糊集A={＜θ，μA(θ)，νA(θ)＞|θ∈Θ}来表示：

其中，μA(θ)为直觉模糊数的隶属度函数，表示的是由支持θ∈A的基本可信度导出的肯定隶属度的下界；νA(θ)为直觉模糊数的非隶属度函数，表示的是由反对θ∈A的基本可信度导出的否定隶属度的下界。

因此，识别框架上的命题A的可信度分配可以直觉模糊数的形式进行表示，即m(A)=＜μA(θ)，νA(θ)＞ 。

3.2 多元素焦元命题的简化

完全基于群决策思想的作战方案评价，由于受客观认知条件的限制以及决策成员的主观认识，进行基本可信度分配时的不确定性将大大增加，表现为单元素焦元命题的基本可信度分配减小，多元素焦元命题的基本可信度分配增大。根据信度函数与直觉模糊数的转换关系，可以将识别框架Θ上的多元素焦元命题转化为若干个以直觉模糊集形式表示的单元素焦元命题，简化后的焦元可信度以直觉模糊数的形式赋值，如下所示：

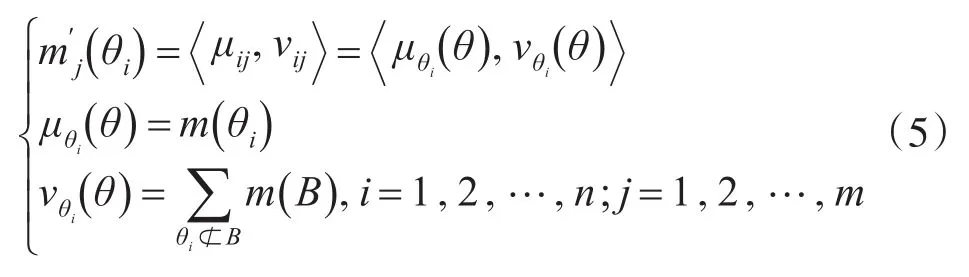
m′被称作直觉模糊基本可信度分配函数，而证据理论中的证据合成将转化为直觉模糊基本可信度分配函数的合成，称之为直觉模糊证据合成。

3.3 证据合成规则的改进

传统的Demster合成规则只能对传统的以基本可信度分配函数形式表示的证据进行合成，现在证据通过前文的转换已经以直觉模糊集的形式表示，因此需要将Dempster合成规则进行修改，以便于直觉模糊证据的合成，如下所示。

wj＞0为群决策成员的权重。

根据直觉模糊集的算术运算法则，有

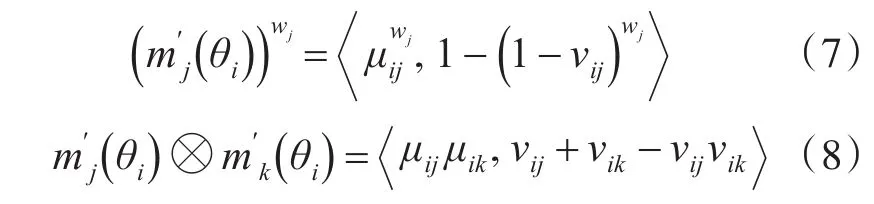
将以上两式代入合成公式，得到

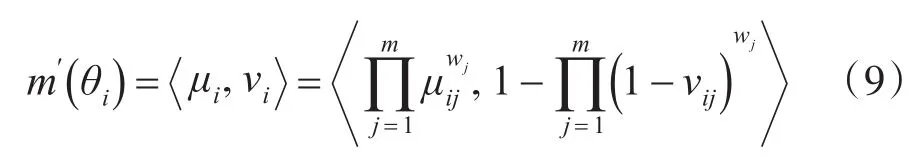
其中μi表示各证据对θi为真信任程度，νi表示各证据对θi为真的不信任程度。

上述合成结果仍是直觉模糊数形式，利用记分函数决策得出最终结果，如下所示：

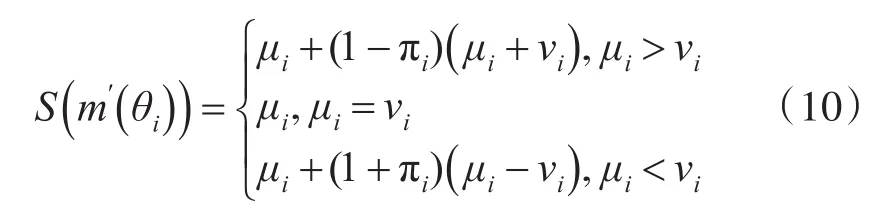
3.4 证据权重的确定

基于群决策方法的作战方案评价过程中，参与评价的各个指挥员由于具有不同的职务、不同的专业侧重以及对被评价对象不同程度的了解，因此各成员的权重通常并不完全相同。本文利用可拓层次分析法对各级评价指标进行权重分析，能够有效降低权重判断中的不准确性且同时考虑到各个指挥员在衡量自己与其他指挥员间权重的灰性，具体方法请参考相关文献［12]，不再赘述。

4 应用分析

以某联合作战方案评价为例为例，方案涉及诸军兵种联合作战，具体作战行动包括电子战、登陆战、封锁战等。现邀请4名指挥官对该作战方案进行评价，评价结果分为5个等级Θ=｛好θ1、较好θ2、一般θ3、较差θ4、差θ5｝。

4.1 确定各指挥员的权重

根据评价要求，各指挥员对其他指挥员相对自身及互相间的重要程度进行两两比较并打分，得到各指挥员间相对重要程度的可拓区间数判断矩阵为A1、A2、A3、A4。

计算得到综合平均可拓判断矩阵如表1所示。

表1 各指挥员综合平均可拓判断矩阵A

根据可拓层次分析法，得到4名指挥员的相对权重为P=（0.4258，0.141，0.3347，0.0985）。

4.2 多证据合成

4名指挥员对该作战方案给出的基本可信度分配如表2所示。

表2 各指挥员给出的基本可信度分配情况

为更好地对比合成结果，将4名指挥员给出的证据以Dempster合成规则和直觉模糊证据分别按照等权重及非等权重（按照上节计算得出的权重）两类进行逐步合成，得出合成结果如表3所示。

4.3 结果分析

等权重条件下，Dempster合成结果与直觉模糊证据合成结果表明该作战方案评价结果为θ1，即“好”。对四组证据进行定性分析可以发现，评价结果为“好”较为合理，说明直觉模糊证据合成算法在此种情况下的合理性与有效性。同时，相对于Dempster合成规则，直觉模糊证据合成算法中最耗时的乘法运算次数大大减少，因此具有更低的计算复杂度。

表3 等权重与非等权重条件下两种合成方法合成结果

在权重不等的条件下，首先分析Dempster合成结果，虽然在三个单元素焦元｛θ1｝、｛θ2｝、｛θ3｝中，经过多个证据合成，最终｛θ1｝的信度最大，即作战方案评价结果为“好”，但是在多元素焦元中，有多个焦元的信度均大于｛θ1｝的信度，这将对最终结果的判断评价上产生一定影响，指挥员可能会因为多元素焦元的信度过大而对评价结果产生犹豫和怀疑，同时也说明这部分多元素焦元携带的可信度信息并没有被完全利用；再分析直觉模糊证据合成结果，结果同样为“好”，但结果避免了多元素焦元的可信度分配，更加有利于指挥员的最终决策，同时将多元素焦元的信度充分利用，计算效率也相对较高。

5 结语

作战方案特别是有关敌方信息，具有不完备性、不精确性、不确定性的特点，证据理论能够将指挥员直观经验作为证据进行多信息融合，一定程度上实现信息极度不透明情况下的作战方案评价。但若证据中存在过多的多元素焦元命题，合成后同样存在过多的多元素焦元命题信度，仍然无法有效解决信息融合后的不确定性问题。证据理论与直觉模糊集理论之间存在着本质的联系，利用直觉模糊集理论在处理不确定和模糊信息方面的优势对证据理论进行改进，可以降低合成结果的不确定性，还能够有效提高证据合成的计算效率，有利于军事决策。对于信息极度模糊、无法通过常规方法进行评价的作战方案，通过该方法将多名指挥员的经验信息进行科学综合，可以在已有限制条件下给出较为合理的评价结果。