反思探究升华思维，归纳猜想凸显本质——兼谈中考复习的习题教学

☉浙江省新昌县南瑞实验学校 张建国

数学中考复习的习题教学一直是备受教师关注、值得研究的一个课题，怎样才能在习题教学课堂中做到既能复习所学的知识，掌握中考所关注的知识点，又能激发学生探究的热情，开阔学生的解题思路，提高学生的解题技能呢？这需要我们不断尝试思考和实践.本文以一道以一次函数与反比例函数图像为背景设计的代数与几何的综合题为例，谈谈在习题的探究过程中，如何引导学生学会从不同的视角来反思问题的解决过程，抓住问题的本质，进而实现解题效益的最大化.

一、典型问题解析

（2017年广东深圳）如图1，一次函数y=kx+b与反比例函数（x＞0）交于点A（2，4）、B（a，1），与x轴、y轴分别交于点C、D.

（2）求证AD=BC.

解析：（1）将点A的坐标代入反比例函数（x＞0），可得m=8.

（2）由（1）的结论可求出C、D两点的坐标为（10，0）、（0，5）.

分别过点A、B作AE⊥y轴于点E，BF⊥x轴于点F，如图2，所以点E（0，4）、F（8，0）.

AE=2，DE=1，BF=1，CF=2.

二、反思与猜想

第（1）问主要考查用待定系数法确定函数的解析式，从中我们不难发现：当函数解析式中含有一个待定字母时，需要知道函数图像上一个点的坐标，含有两个待定字母时，则需要知道两个点的坐标，这样可以转化为一元一次方程或二元一次方程组解决问题.

对于第（2）问，从计算过程中我们可以发现AE=CF=2，DE=BF=1，又∠AED=∠CFB=90°，显然△CFB，所以AD=CB，根据等量代换我们可以进一步推理得到：AC=BD.

一位数学家曾说过：学之道在于“悟”，可见在数学学习过程中，学生的反思对于理解与掌握数学知识非常重要而且是必需的.只有通过反思，学生的思维才能真正启动，思想才能得到升华，问题才能得到深化，经过推理与猜想，才能把问题从特殊到一般进行推广.本题是以具体的一次函数图像——直线与反比例函数图像——双曲线相交创设的一个数形结合问题情境中探究线段之间的相等关系的数学问题，解题的过程中体现出的解题思路是先确定函数的解析式，进而确定直线与x轴、y轴的交点及与反比例函数的交点的坐标，通过定量计算x轴、y轴上的线段CF、DE的长度和平行于y轴、x轴的线段BF、AE的长度，再借助勾股定理求得线段AD、BC的长度来证明的.辨证唯物主义告诉我们：人认识事物的过程，是从具体到抽象，从个别特殊到一般，然后又用这一般的、共性的东西去研究新的个别的、特殊的事物，从而补充、丰富和发展对这种共同的本质的认识.任何特殊都包含着一般，一般存在于每一特殊之中.一般与特殊的这种辨证关系启示我们，解题应当善于对问题从具体的、个别的入手获得问题的结论和解决问题的方法，然后在其基础上推广猜想一般的结论，并进行推理，证明猜想的正确性.

由此我们能否将上述特殊问题——引例的结论，进行推广猜想：一般的，一次函数y=kx+b的图像（直线）与反比例函数的图像的两个交点及与x轴、y轴的交点所构成的线段之间是否同样具有上述关系呢？下面我们再来探究如下一个命题，学生便可以一目了然，给出肯定的回答.

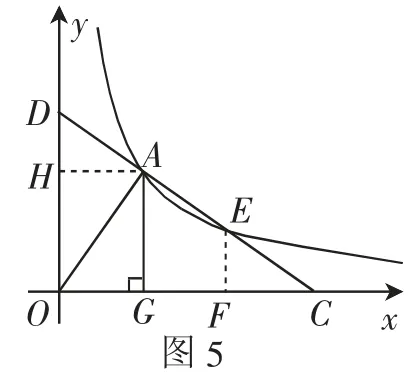
（2017年江苏徐州）如图3，直线l交x轴于点C，交y轴于点D，与反比例函数的图像交于A、E两点，AG⊥x轴于点G，S△AOG=3.

（1）求k的值；

（2）求证AD=CE；

（3）如图4，若点E为平行四边形OABC的对角线AC的中点，求平行四边形OABC的面积.

解析：（1）设点A的坐标为（x，y）.

（2）思路1：证明两条线段相等，通常可以借助三角形全等来解决，我们不妨构造包含AD、CE在内的两个三角形，然后证明两个三角形全等.为此分别过A、E两点作y轴、x轴的垂线，垂足分别为点H、F，便可以获得Rt△DHA、Rt△EFC，如图5所示，下面证明这两个三角形全等.

解法1：因为反比例函数的解析式为，设点A的横坐标为a，则其纵坐标为.

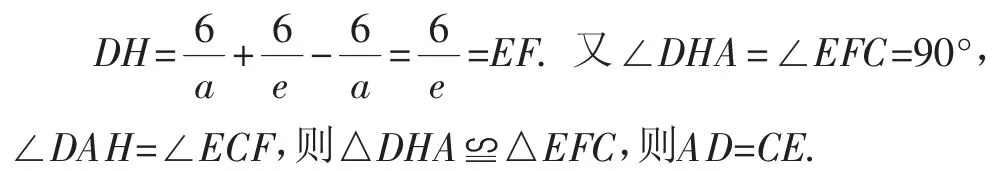
解法2：以上同解法1，令y=0，可得点C的坐标为（a+e，0），则CF=a+e-e=a.而AH=a，则AH=CF.又∠DHA=∠EFC=90°，∠DAH=∠ECF，则△DHA△EFC，则AD=CE.

思路2：借助中间媒介——a=b，b=c，则a=c来证明.

如图6，过点E作y轴的垂线，垂足为点H，交AG于点F，连接GH.

思路3：利用比例线段证明线段相等——若则a=b.

如图7，分别过A、E两点作y轴、x轴的垂线，垂足分别为点N、K，两垂线相交于点M，再过点E作y轴的垂线EH，垂足为点H，交AG于点F.

由反比例函数k的几何意义可知：

S矩形ONAG=S矩形OHEK=6，则S矩形HNAF=S矩形FEKG.则AN·AF=FE·EK.又AF=ME，FE=AM，则AN·ME=AM·EK，即

（3）解法1：由AG∥OD，可知

由点E是AC的中点，得CE=AE.

结合（2）的结论AD=CE，得AC=2AD.

则CG=2OG.又△ACG与△AOG等高，则S△ACG=2S△AOG=6.

则S△AOC=S△ACG+S△AOG=9.

又平行四边形OABC的对角线把平行四边形分成两个全等的三角形，则S平行四边形OABC=2S△AOC=18.

解法2：如图8，连接OB，过点E、B分别作EF⊥x轴、BP⊥x轴，垂足分别为点F、P.

又S△BCP=S△AOG=3，则S△OBC=9.

又平行四边形OABC的对角线把平行四边形分成两个全等的三角形，则S平行四边形OABC=2S△OBC=18.

解题过程的反思：第（1）问考查学生对反比例函数解析式中k的几何意义的探究，如图9，若点P（x0，y0）是反比例函数上任意一点，则有x0·y0=k，即x0与y0的积必是一个定值.过点P分别作x轴和y轴的垂线，垂足分别为点M、N，则PM=ON=｜y0｜，PN=OM=｜x0｜.故S△PMO=S△PNO=，此时S矩形PMON=｜x0｜·｜y0｜=｜k｜.这就是说，过双曲线上任意一点作x轴和y轴的垂线，两垂线与坐标轴围成的矩形的面积等于｜k｜，或以该点与垂足、坐标原点为顶点的直角三角形的面积等于｜，这是比例系数k的意义.

第（2）问探究两条线段相等的问题，常见的证明思路是通过证明三角形全等来证明.思路1为此构造了Rt△DHA、Rt△EFC，容易证明这两个直角三角形相似，因此只要再证明有一条直角边相等即可得出两条线段相等，而说明直角边相等则利用了解析法，即先用点A、E的坐标求出直线CD的解析式，接着求出点D或点C的坐标，最后借助坐标轴上两点间距离完成证明.计算量较大，且涉及的字母较多，非一般的计算推理能力所企及，这是本思路一个难以逾越的鸿沟，所以造成多数学生虽有证明全等的欲望，却半途而废，形成的思路夭折.

思路2，怎样想到转化线段AD、CE使其都与GH发生关系，确是本思路的难点之一，通过说明GH∥CD是第二个难点，利用解析法计算出两边对应成比例也是较为棘手的一个方面，所以本思路相对于思路1，学生更加感到困难.从所阅试卷答案来看，没有发现学生证明的踪迹.

至于思路3，不少学生想到了通过三角形相似，利用比例线段来证明，但推理路途崩溃，主要原因是没有构造出适当的相似三角形，没有巧妙地利用k的几何意义得出S矩形HNAF=S矩形FEKG，进而得到，造成比例线段中间比不能有效传递，思维受阻，同样这种解法在考生的答卷中，仅有极少数学生获得成功.从学生的答题情况看，这道题的信度和效度是不尽如人意的.

三、发现结论

由引例1、2我们发现：一次函数的图像（直线）与反比例函数的图像的一支的两个交点，分别到直线与两坐标轴交点之间的距离相等.由于反比例函数图像是双曲线，由此我们不难联想：任意一条直线与反比例函数图像的两支曲线的交点，到与两坐标轴交点之间的距离是否相等呢？答案是肯定的，证明过程留给读者完成.

综合引例1、2的结论及推广猜想与证明，我们可以归纳出如下一个重要的正确命题：经过反比例函数图像上两点的直线与两坐标轴相交，这两点到不在同一坐标轴上的交点的距离相等.

四、教学启示

上面习题的探究过程启发我们在中考复习的习题教学过程中，应精心挑选一些具有典型性、值得研究的中考试题作为例题，以学生原有的知识和经验作为新知识的生长点，使设计的问题永远处于维果斯基提出的“学生最近发展区”.有意识地将原问题拓展延伸，引导学生从简单的问题入手，通过对数学问题多角度、多层次、多方位的讨论和思考，层层推进，不断揭示问题的本质，并引导学生进行解题后的反思，在学生具有亲身感悟的基础上，进行突出数学本质的提炼和数学思想的概括.使学生在解题中学会解题，强化学生的思维能力，达到解题技能的游刃有余，学会以不变应万变.进而使学生的认知能力更上一层楼，为全面提升学生的核心素养，实现课堂的有效教学添砖加瓦.