诊评与改进：习题讲评听、评课的追求——以两则解题教学片段为例

☉甘肃省高台县第三中学 陈 波

中考复习期间会遇到不少较难的函数填空题，通常位于一些模考试卷的填空题的最后一题位置.而有些讲评往往只是满足于答案的获得，缺少对问题更有深度的回顾与反思，常常是“入宝山而空返”.本文整理近期在中考复习期间的听课所见、所闻与所思，供分享和研讨.

一、较难填空题讲评的听课记录与诊评改进

说明：以下听课记录并不是同一节课中收集的，也不是来自同一个老师或班级.

案例1：在平面直角坐标系xOy中，抛物线y=ax2+4ax+4a+1（a＜0）交x轴于A、B两点，若此抛物线在点A、B之间的部分与线段AB所围成的区域内（包括边界）有且只有8个整点（横、纵坐标都是整数的点），则a的取值范围是_______.

师：这道题没有一名同学做对，我们一起来探究.由已知条件可以得到什么？

生1：因为a＜0，所以抛物线开口向下，可以画出抛物线的大致图像，先将函数解析式配方成顶点式y=ax2+4ax+4a+1=a（x+2）2+1，所以抛物线的对称轴为直线x=-2，顶点是（-2，1），假设交点A在左边，点B在右边，则点A，然后我就不会了.

师：很好，请坐，你得到的这些结论很有用，是我们接下来解题的依据.请大家思考一下，抛物线在点A、B之间的部分与线段AB所围成的区域内（包括边界）有且只有8个整点，这8个整点的横、纵坐标需要满足什么条件呢？

生2：这8个点的纵坐标只能是0或1，纵坐标为1的整点只有1个，是（-2，1），还有7个点的纵坐标是0，且在线段AB上，线段AB的中点为（-2，0），符合要求，所以左边还有3个点，横坐标是-3、-4、-5；右边还有3个点，横坐标是-1、0、1，所以

师：非常好！解这个题目的关键在于找到这8个整点的位置，分析到最后类似于我们常做的不等式组有3个整数解的问题.很多看起来很难的题目，一层层剖析开，最后还是回到了我们常做的一些题目.面对最后一道选择题和最后一道填空题不要害怕，看好条件慢慢分析，会有办法解决的.

课堂诊评与教学改进：这道较难题的讲评虽然也有师生对话、互动讲评，也得到了这道较难题的答案，但是对很多学生来说，效果并不明显，因为正如生1一样，当得到了两个交点A、B的坐标之后，后续求解仍然是难理解的，因为生2所提出的不等式是一个含根号的陌生的繁难不等式，教学的难点之一也在于此.教师在备课时需要深刻理解这道习题，想清辨明这道习题的理解难点与教学难点.我们认为，这个问题难点有以下两处：

难点之一，带领学生想清围成区域内整点分布的位置.具体来说，围成区域内部是不存在整点的，整点都在边界上，而作为边界之一的抛物线的顶点就是符合要求的一个整点，然后就是x轴上存在整点，这样就把目光聚焦到数轴上分析整点个数，进而基于对称性分析出抛物线与x 轴的交点（右边的）的横坐标介于1和2之间（如图1）.

图1

难点之二，带领学生想清抛物线与x轴的一个交点的横坐标的取值范围是1≤x＜2.进一步如果利用上面生1、生2的方法，会出现繁杂不等式.可以借助抛物线“穿过”x轴前后分别在x轴上方或下方来构造不等式组，这就是当x=1时，函数值大于或等于0；当x=2时，函数值小于0.

案例2：已知点A在函数的图像上，则y1、y2、y3的大小关系是______.如果点A（a，y1）、B（a+1，y2），则y1、y2的大小关系是______.

师：这道填空题第一问大家完成得很好，但是第二问有不少学生做错了，大家对这个题目的第二问有什么想法？

生1：我觉得可以先画出草图，然后分情况讨论：

①A、B两点都在y轴的左侧，当a＜0，a+1＜0，即a＜-1时，y1＞y2.

②点A在y轴的左侧，点B在y轴的右侧，当a＜0＜a+1，即-1＜a＜0时，

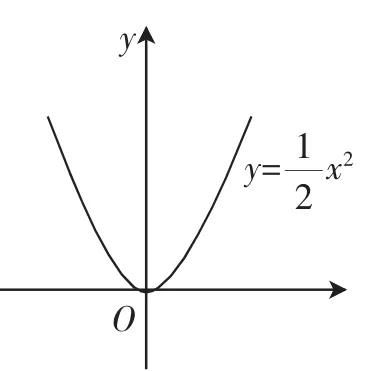
图2

1°若-1＜a＜-0.5，则y1＞y2；

2°若a=-0.5，则y1=y2；

3°若-0.5＜a＜0，则y1＜y2.

③A、B两点都在y轴的右侧，当a＞0，a+1＞0，即a＞0时，y1＜y2.

师：很好，这名同学根据A、B两点不同的位置情况分了五种情况讨论，考虑得很全面.但是我们要注意答题时要总结，合并结论.其他同学再想想，他的方法能不能更优化？

②当a＜-0.5时，点A离对称轴更远，则y1＞y2；

③当a＞-0.5时，点B离对称轴更远，则y1＜y2.

师：很好.这名同学充分利用函数图像的性质，简洁、明了地解决了问题.所以我们一定要熟练运用函数图像，有时候解题会事半功倍.

课堂诊评与教学改进：虽然学生利用函数图像顺利解决了问题，但并不如教师点评的那样“熟练运用函数图像，有时候解题会事半功倍”.事实上，学生针对这道习题利用画图分析的“以形助数”方法并不是最优的，教师应该有解法最简、最优的专业评价，对于这道习题，直接代入计算并利用“作差法”是更简更优解法.解法如下.由题意得，接下来讨论与0的大小，即可比较出y1与y2的大小.

二、关于解题教学的进一步思考

1.教师对较难题要有深刻理解

从上面两则听课案例来看，教师本人对这两道较难题的理解并没有达到深刻程度.具体来说，较难题的深刻理解，包括解题思路的贯通，特别是多种解法的预设，对问题深层结构或本质的洞察，还有对问题考查的知识点、方法或策略都要有全面的分析，对考题不同解法的繁简要有对比，从学情出发精准研判学生可能的障碍点、关键步骤、易错点，等等，这些都是在解题教学备课时要下足功夫的.否则开课之后就会出现一些泛泛的评论、“乱点赞”式的评析.

2.教学时针对学生进展来引导

在听课中发现，两位教师解题教学进程中，先让学生表达解法、思路或解题念头是可行的一种教学组织，而不是教师一言堂.然后，当学生不能顺利推进解题思路，思维受阻时，教师的引导就非常关键，而不只是把这个疑难点推向其他优秀学生，继续推进解法，直至思路贯通，讲题结束.我们认为，可以针对学生思路受阻的步骤进行深入分析，引导更多学生参与评析.为什么进展不了？这些繁难解法能否有效转化，避免自己陷入繁难？多引导学生思考这些问题，不仅有助于最终问题获解，而且能让学生通过解题学会解题，在以后独立面对陌生问题时，学会自主调控解题节奏与获得解题念头.

3.解后回顾时要注意比较优化

在上文记录的两段解题教学的最后，教师都没有安排解后回顾的环节，这也是造成“入宝山而空返”的原因.对于案例1中的函数难题，要在解后回顾中安排学生想清辨明哪些步骤是该题的关键步骤，哪些地方是易错之处，这样学生就多了深入反思解题步骤的机会，也能“事后诸葛”分析出这类问题的“破题”关键.而对于案例2中的习题，虽然教师安排了另一个学生再次讲解不同思路，但是只是原有“数形结合”思路上一次改进或简化，没有从方法上进行大的思考方向的调整：从“以形助数”走向“以数驭形”.