例谈初中数学课堂教学资源的改编

（山东省东营市教育科学研究院；山东省东营市胜利第六中学）

当前，各种教辅资料质量参差不齐，影响了教育教学生态.一线教师应该从加大对教材的研究力度，着手改变上述不良现象.例如，教学中对教材提供的教学资源进行再用、变用、异用等.教材是最优质的课堂教学资源，教材的编写具有一定的普适性，因此一线教师可以在充分理解教材的前提下，结合学生的实际情况对教材中的教学资源进行适当改编.本文结合具体的实践案例进行简单的介绍，并给出初步的思考，不当之处，敬请指正.

一、案例呈现

案例1：“中心对称”新授课.

“中心对称”是人教版《义务教育教科书·数学》（以下统称“人教版教材”）九年级上册第23章第2节（第1课时）的内容.人教版教材九年级上册中将其作为一种特殊的“旋转”（旋转角为180°）进行介绍，这样学生可以比较容易地得到与其相关的概念和性质，紧接着人教版教材九年级上册第65页呈现了例1，作为对中心对称相关性质的简单应用和强化巩固.例1的内容如下.

（1）如图1，选择点O为对称中心，画出点A的对称中心点A′.

（2）如图2，选择点O为对称中心，画出与△ABC关于点O对称的△A′B′C′.

图1

图2

可以看出，上述例1仅仅实现了对中心对称性质的“正用”，同时只包含对称中心在图形外部的情况.于是在教学中，笔者对此例题进行了如下改编.

在完成例1第（2）小题教学的基础上，笔者将学生所添加的辅助线擦去，得到如图3所示的图形.

图3

改编1：如果知道图3中的这两个三角形关于某点对称，你能找出它的对称中心吗？为什么？

这个改编与教材第66页的练习2（图4中的两个四边形关于某点对称，找出它们的对称中心）相对应.

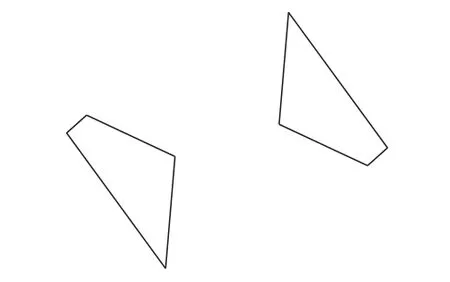
图4

改编2：如果将例1中第（2）小题的对称中心改为点A，你能画出与△ABC关于点A对称的△AB′C′吗？

这样改编有如下两个目的：一是让学生清楚对称中心可以在图形上；二是引导学生回顾已学知识，与人教版教材八年级上册第38页例2相对应，具体内容如下.

如图5，有一池塘，要测池塘两端A，B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD=CA.连接BC并延长到点E，使CE=CB.连接DE，那么量出DE的长就是A，B的距离.为什么？

图5

改编3：如果将例1中第（2）小题的对称中心改为边AB的中点呢？试着说明你所得到图形的形状.

这样改编有如下三个目的：一是让学生进一步明确对称中心可以在图形上；二是进一步引导学生回顾已学知识，让学生从中心对称的角度理解平行四边形所具有的性质；三是为下一节课将要学习的中心对称图形做铺垫，让学生初步感知平行四边形是中心对称图形.

然后，教师为了加深学生对改编3的认识，给出如下拓展题.

拓展：如图6，在△ABC中，AB=4，AC=6，AD是边BC的中线，求AD的取值范围.

图6

【评析】案例1中，对教材中教学资源的改编主要以三个问题的形式呈现.改编1考查学生的逆向思维能力，这是在解决问题中经常用到的方法；改编2和改编3以改变对称中心位置的形式呈现，丰富学生的认知.同时，改编2引导学生回顾已学知识，做到了课堂教学逻辑连贯和前后一致.最后的拓展题深化了学生对改编3的认识，将学生的思维引向深处，让学生初步感知“倍长中线”的方法，达到了变式改编的较高效益.

案例2：“等腰三角形”复习课.

“等腰三角形”是人教版教材八年级上册第13章第3节的内容.学生在小学阶段已经对等腰三角形的定义有了初步的了解，于是人教版教材八年级上册中引导学生从轴对称的角度去研究等腰三角形所具有的性质（等边对等角和“三线合一”），然后从交换命题的条件和结论的角度研究等腰三角形的判定定理（等角对等边）.“等腰三角形”复习课是在新授课结束后，对等腰三角形从定义、性质和判定三个角度进行复习的综合复习课.笔者从教材出发，对人教版教材八年级上册第89页的活动3进行改编，通过“一题一图”将等腰三角形的定义、性质和判定一网打尽，实现了较好的教学效果.活动3内容如下.

猜想一下，等腰三角形底边中点到两腰的距离相等吗？如图7，你可以将等腰三角形ABC沿对称轴AD折叠.观察DE和DF的关系，并证明你的结论.

图7

如果DE，DF分别是AB，AC上的中线或∠ADB，∠ADC的平分线，它们还相等吗？由等腰三角形是轴对称图形，利用类似的方法，还可以得到等腰三角形中哪些线段相等？证明其中的一些结论.

将上述活动3用符号语言表示，可得如下题目.在此称为“原题”.

原题如图8，在△ABC中，AB=AC，D是边BC的中点，DE，DF分别是边AB，AC的垂线，求证：DE=DF.

图8

思路1：不添加辅助线，证明△BED≌△CFD（AAS）即可.

思路2：如图9，连接AD，证明△AED≌△AFD（AAS）即可.

图9

思路3：如图9，连接AD，直接应用角平分线的性质即可.

思路4：如图9，连接AD，利用△ABD和△ACD的面积相等即可.

思路1引导学生复习等腰三角形的性质“等边对等角”；思路2和思路3引导学生复习等腰三角形的性质“三线合一”；思路4为后续教学拓展1和拓展2，以及为后面勾股定理的证明打下一定的基础.

学生解题后，教师针对原题进行如下改编.

改编1：如图10，在原题的基础上，若连接EF，你还能得到哪些结论，或者图中还有哪些等腰三角形？

图10

改编2：如图8，在△ABC中，DE=DF，D是边BC的中点，DE，DF分别是边AB，AC的垂线，求证：AB=AC.

改编3：如图8，在△ABC中，DE=DF，AB=AC，DE，DF分别是边AB，AC的垂线，求证：D是边BC的中点.

改编4：回到原题，连接AD，将条件“DE，DF分别是边AB，AC的垂线”改为“DE，DF分别是∠ADB和∠ADC的角平分线”，其他不变，DE=DF还成立吗？如何证明.

改编5：回到原题，将条件“DE，DF分别是边AB，AC的垂线”改为“DE，DF分别是△ADB和△ADC的边AB，AC的中线”，其他不变，DE=DF还成立吗？如何证明.

通过改编1，引导学生复习等腰三角形的定义；改编2交换了原题中的条件和结论，引导学生复习等腰三角形的判定“等角对等边”；改编3中，继续交换原题中的条件和结论，引导学生复习等腰三角形的性质“等边对等角”.改编4和改编5则是改变原题的条件，引导学生进行更深入的思考.然后，为了巩固学生对解法4的认识，教师又给出如下两道拓展题.

拓展1：如图11，在△ABC中，AB=AC，D是边BC的中点，DE，DF分别是边AB，AC的垂线，CG⊥AB，垂足为点G，证明：CG=DE+DF.

图11

图12

拓展2：如图12，在△ABC中，AB=AC，D是边BC上的任意一点，DE，DF分别是边AB，AC的垂线，CG⊥AB，垂足为点G，结论CG=DE+DF还成立吗？

【评析】案例2延用了案例1中对教学资源改编的基本架构：原题+改编+拓展.其中“原题”来源于教材，是最基础的教学资源，要求所有学生都要掌握；“改编”主要以问题串的形式呈现，加深学生对相关问题的理解.

案例2中，通过对等腰三角形中的重要线段（角平分线、高线、中线）的研究，延伸到对等腰三角形中任意“对应线段”的研究，从而加深学生对等腰三角形是轴对称图形这一性质的认识；“拓展”则是对学生提出更高的要求，在掌握较低要求的同时，让学有余力的学生有进一步的获得感，可以看出这样的设计也是层层递进的，做到课堂教学的一以贯之，甚至让学生聆听到课堂学习中知识“拔节”的声音.

二、两点思考

1.源于教材，超越教材

教材是编写者集体智慧的结晶.教学中，一线教师应该重视教材，研究教材，实现和教材及教材编写者的对话，而不是“唯教辅资料是从”.在上述两个案例中，笔者对教材中的教学资源进行了改编，通过一个个追问将学生的思维引向深处，做到了课堂教学内容“源于教材”；接着，笔者又对教材中的教学资源进行更深层次的改编，并给出拓展题，引导学生回顾已学知识，并为后续知识的学习做铺垫，实现了课堂教学内容“超越教材”，取得了良好的课堂教学效果.

2.基于变式，成于改编

变式教学是数学教育的一个典型特色之一.在上述两个案例中，笔者很好地进行了变式教学.例如，不添加条件还能得到什么结论？交换题目的条件和结论，是否仍然成立？改变题目的条件，你还能得到哪些结论？等等.这些设问方式可以看作是对变式教学的积极践行.但是，笔者始终认为变式教学应该在尊重教材、理解教材的基础上展开，在此基础上再进行适当的改编，做到基于变式，成于改编，向部分学生提出更高的要求，这与《义务教育数学课程标准（2011年版）》所提倡的“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”的课程基本理念也是不谋而合的.