磁悬浮飞轮永磁同步电机充放电瞬态切换问题研究
李树胜,刘 平,付永领,李光军
(1.北京航空航天大学,北京 100083; 2.中电建路桥集团有限公司,北京 100048;3.北京泓慧国际能源技术发展有限公司,北京 101300)
0 引 言
与其他储能方式相比,磁悬浮飞轮储能[1-5]是一种新型的机械储能技术,具有充放电迅速、储能密度大、放电深度高、环境污染小、易于维护等优点,可应用于UPS电源、轨道交通制动能回收、电力系统调峰、石油钻井功率补偿等领域[6-10]。
高速永磁同步电机(以下简称PMSM)具有功率密度大、几何尺寸小、质量轻、响应快、调速范围宽等显著优点[11-15],在航空航天、工业自动化以及电动汽车等领域应用广泛,PMSM是飞轮高速旋转驱动机构的理想选择。飞轮充电时,PMSM处于电动状态,驱动飞轮高速旋转,将电能转化成动能存储;飞轮放电时,PMSM切换成发电状态,飞轮转子降速,并将机械能转化为电能。因此,PMSM的频繁充放电控制是实现飞轮储能的关键技术之一。
在实际应用中,由于飞轮转子惯量较大,转速较高,PMSM需要在几个毫秒内由电动状态切换至发电状态,使得电机d,q轴电流耦合效应明显,电流调节器存在较大超调振荡,严重时会导致电流冲击过大而损坏设备[16-20]。另一方面,飞轮所用电机多数为非标电机,需要兼顾功率、尺寸和体积等多方面特性,在反电动势、永磁体气隙磁密方面难以做到最优化设计,容易造成电机特性较软,在突加大功率负载放电时电机反电动势会迅速降低,导致充放电切换瞬间电流存在较大的换相尖峰。同时,电机在长时间带载情况下难免出现永磁体退磁现象,当定子电流临近磁滞曲线边缘时退磁现象会进一步恶化,同样会降低电流调节器控制性能,影响电机充放电平稳切换过程。
针对以上问题,所查阅文献研究内容多集中于第一种现象,多是对电机在稳态时d,q轴电流耦合引入的控制性能下降问题展开研究,而对于电机在带载条件下进行充放电切换瞬间引入的电压降低、电流尖峰等问题的研究较少。本文针对电流尖峰问题,首先对飞轮PMSM充放电原理和控制策略进行了介绍,对电机充放电切换时电压、电流的相位变化进行了分析,提出一种基于转子磁链相位补偿的电机充放电切换策略,有效降低了充放电带载切换瞬间的电流尖峰,弥补了电机软特性引入的电流冲击的缺陷。
1 系统建模和问题描述
1.1 系统建模
磁悬浮储能飞轮整体结构和内部原理如图1所示[5],由密封壳体、定子、高速转子、永磁体、五自由度全电磁轴承、高压真空电极和备用轴承等组成。其中,五自由度全电磁轴承由径向和轴向磁轴承以及位移传感器组成,用于保持高速转子的全悬浮状态。PMSM作为飞轮转子驱动机构,通过电机的充放电控制实现电能与动能的相互转化。备用轴承用于保护电磁轴承,防止转子跌落损坏磁轴承。密封壳体用于固定飞轮组件,同时使腔体保持一定的真空水平。

(a) 飞轮整体图

(b) 内部结构图
图1磁悬浮储能飞轮示意图
基于高速旋转时的转子强度问题,飞轮PMSM普遍采用表贴式PMSM(以下简称SPMSM),永磁体外侧采用高强度护套紧固。PMSM定子通过热处理工艺安装于壳体内侧,外侧引出三相绕组用于通入三相正弦对称电流。飞轮PMSM最小功率拓扑结构如图2所示,输入/输出为直流DC+,DC-电源接口。充电时,直流电能经过6组IGBT开关管进行逆变后流入PMSM,飞轮转子升速,将电能转化为动能存储;放电时,飞轮转子所存储动能经过IGBT开关管整流后输送至直流电源端口,以维持直流母线电压恒定,飞轮转子的动能转化为直流侧负载电能。

图2 飞轮PMSM最小功率拓扑结构
SPMSM在三相静止坐标系下的电压方程如下[21]:

(1)
式中:ua,ub,uc为定子三相电压;ia,ib,ic为定子三相电流;Ls,Rs为定子电感和电阻;φf为永磁体磁链;θr,ωr为转子角位置和电角速度。
对于传统的PMSM矢量控制方案,通常将三相静止坐标系转换为两相同步旋转坐标系,将电机励磁分量与有效转矩分量进行分开,实现高精度解耦控制。SPMSM在d,q坐标系下的电压和转矩方程如下[21]:

(2)
式中:ud,uq分别为直轴和交轴电压;id,iq分别为直轴和交轴电流;p为电机极对数;Te为有效电磁转矩;Td为电机干扰力矩(包含飞轮转子动力学耦合力矩等);Ld,Lq分别为直轴和交轴电感,对于凸极效应较弱的SPMSM,通常有Ld=Lq。
1.2 飞轮充放电瞬态切换问题分析
飞轮储能装置采用SVPWM矢量算法,完成电机升降速控制,实现飞轮电动/发电状态的瞬态切换,其控制结构如图3所示[5]。

图3 飞轮PMSM充放电控制结构图
飞轮充电过程采用“速度外环+双电流内环”控制策略。PMSM位置和速度信息可选用旋转变压器或绝对式编码器进行采集,同时可通过设计位置和速度估计器获得电机位置和转速实时估计值。双电流环包括Iq电流环和Id电流环,其中,Iq电流环用于控制电机的有效电磁转矩,Id电流环用于控制电机的励磁分量。为获得良好的功率因数与效率特性,Id电流环通常采用Id=0控制方案,即保持电机励磁分量最小,电机定子所消耗电流均用于转子加速。
飞轮放电过程采用“电压外环+双电流内环”控制策略。Id电流环仍然采用Id=0控制方案,Iq电流环参考值Iqref由转速环输出值切换至电压环输出值,以维持直流母线电压恒定,完成电机由电动状态向发电状态切换。
充电模式与放电模式下,电机端电压(相电压)、定子电流(相电流)以及反电动势(相反电动势)的方向示意如图4所示。充电模式下,电机处于电动状态,端电压U,反电动势E及电流I是同向的,且端电压幅值大于反电动势,电能由直流母线侧流入电机侧。放电模式下,电机处于发电状态,相对于端电压U而言,此时反电动势E与电流I是反向的,电能由电机定子流入直流母线侧。

(a) 电动状态

(b) 发电状态
从图4可以看出,电机由电动向发电状态切换瞬间,电流方向由流入定子侧迅速反向,依靠定子电感和电机反电动势组成boost升压电路,完成电压泵升过程,如图5所示。

图5 电机发电等效boost升压电路图
实际情况中,由于飞轮需要在几个毫秒内满额功率放电,而电机实际特性较软,在放电瞬间出现的大电流造成反电动势迅速降低,导致电压泵升过程中出现电流尖峰。这种电流尖峰随着负载功率变大而加剧,当负载功率达到一定值后会造成变流器过流保护。如图6所示,市电供电600 V,电机以较小电流浮充电,飞轮维持某一转速稳速旋转,在85 500计数时刻飞轮以一定电流充电(60 A左右)至额定转速稳速运行,在图6中85 600计数时刻进入“放电稳压”,主回路供电切断,飞轮迅速切换到放电模式,电机iq电流值反向并不断增大,以维持直流母线电压不变(飞轮放电稳压500 V)。而在电机放电切换瞬间,由于反电动势的降低,id与iq电流均出现电流尖峰(未满额放电,尖峰没有达到限幅值)。

图6 充放电切换电流尖峰
2 基于转子磁链相位补偿的充放电瞬态切换方法
转子磁链相位补偿的基本思路是在获取机PMSM转子磁链真实位置前提下,根据d,q轴电压大小计算出角度补偿量,并对转子磁链位置进行相位补偿。
PMSM控制系统在实现转子磁场定向控制时,其控制结构如图3所示,数学模型如式(2)所示。图3中,iq和id电流环经补偿器Giq(s),Gid(s)分别生成d,q轴控制电压Vq和Vd,这两组控制电压即为期望矢量的转矩电压和励磁电压。
根据PMSM特性可知,其电动势与频率之间满足如下关系:
E=4.44NΦKef
(3)
式中:N为定子线圈匝数;Φ为磁通;Ke为基波绕组系数;f为电流频率。
为了提高定子磁场利用效率,同时避免磁场饱和,在给定子通电时通常需要保证E/f=常数,即增加频率的同时增加定子电压。在理想控制状态下,采用Id=0控制方案可以达到id测量值基本为零,iq测量值在充电过程中保持不变,因此式(2)可以进一步简化:

(4)
式中:iqc为充电最大电流。
因此,在转子永磁体磁链保持不变且最大充电电流一定的前提下,其d,q坐标系施加的转矩电压Vq和励磁电压Vd随转速的变化率是固定的,分别为Δωrφf,-ΔωrLqiqc。可以认为,在某一个转速下,转矩电压Vq和励磁电压Vd的变化量是确定的,即:

(5)
因此,在当前转速值ωr、交轴电感Lq、定子电阻Rs、磁链φf以及最大充电电流iqc条件下,可以求得转矩电压Vq和励磁电压Vd的理论值,该转矩值取决于上述参数大小。
但在实际应用中,由于电机特性较软,在大功率充放电过程中,电机反电动势会瞬间拉低,转子磁链会被削弱,导致转矩电压Vq和励磁电压Vd发生变化,在切换瞬间容易造成电流尖峰。另一方面,在电动和发电运行状态下,转子磁链角位置θr的值决定了控制系统设定的d,q系的d轴与实际转子磁链轴之间的夹角关系(如图7所示),在θr与实际转子磁链角位置相等时,d轴与转子磁链轴完全重合。可以适当改变θr的值,改变励磁电压在转子磁链方向的分量,但是只要与转子磁链在转速上严格同步,不影响电机正常运行。因此,针对充放电切换瞬间由于电机特性较软而引入的反电势拉低现象,可以通过调整θr的值,改变磁链电压Vd,使转子磁场得到进一步增强,从而保持电机电势不变,抑制换相电流尖峰。
基于此,转子磁链角位置补偿量计算如下:

(6)
式中:Vq0,Vd0为初始电压(可在线标定或理论计算),其矢量描述如图7所示。理想情况下在额定转速时,|Vq1|=|Vd1|(已经通过标定Vq0,Vd0使两者相等),则相位补偿量Δθr=0;若|Vq1|<|Vd1|,则表明实际转子磁场与理论设计值存在差异,实际磁场变弱,需增加正向激励磁场,Δθr>0;若|Vq1|>|Vd1|,则表明实际转子磁场增强,需增加负向激励磁场,Δθr<0。

图7 Vd,Vq矢量描述图
在实际应用中,通常引入电压误差阈值Vth,满足如下关系:

(7)
从式(7)可知,将Vq1,Vd1的差值与设定的阈值Vth比较,若Vq和Vd的差超过Vth,说明Vq增加量明显大于Vd,需要减弱磁场(这种情况基本不会出现);若Vq和Vd的差远低于Vth,说明Vq增加量明显低于Vd,需要增强磁场,以补偿反电动势降低。
基于以上分析,将角位置相位补偿量反馈到图3中的位置估计器中,得到补偿后的转子磁链角位置:

(8)
基于转子磁链角位置相位补偿的充放电矢量控制方法如下,可根据实验测试得到电压阈值Vth>0。
第一步:调节初始电压Vq0,Vd0。按照充电控制逻辑将飞轮转速升至转速n0(n0<1 000 r/min),设定此时的Vqn,Vdn的值为初始电压,即Vq0=Vqn,Vd0=Vdn。
第二步:根据式(4)在线监测转矩电压Vq和励磁电压Vd,并根据式(6)计算电压值Vq1和Vd1。
第三步:根据第二步得到的Vq1和Vd1,按照式(7)计算角位置相位补偿量Δθr。

以上为本文核心算法,下面将所设计的控制系统应用到实际对象中进行实验验证。
3 磁悬浮储能飞轮实验装置及参数
本文在北京航空航天大学、北京泓慧国际能源技术发展有限公司以及中电建路桥集团支持下,以自研的磁悬浮储能飞轮为实验对象进行实验验证,实验装置如图8所示,飞轮系统包括飞轮本体、充放电变流器、磁悬浮系统、真空系统以及主控屏幕系统等组成,飞轮参数如表1所示。

图8 磁悬浮储能飞轮实验装置

表1 飞轮系统参数
本实验采用“在线双变换UPS+飞轮电池+三相负载”的组合形式,电网380 V(AC)输入经过UPS整流AC/DC升压600 V(DC),一方面经逆变器DC/AC供给三相负载,另一方面接入飞轮双向DC/AC变流器,如图9所示。
飞轮充放电控制系统采用基于转子角位置相位补偿的矢量控制算法,充电时电能经UPS整流、飞轮电池逆变转化为飞轮动能存储,直流母线电压保持600V(DC);待飞轮升至额定转速后,切断电网供电,UPS自动转由飞轮电池供电,直流母线电压设置为500 V(DC),持续给负载供电,保证不间断电源供应。考虑到安全和可靠性,三相负载的功率选择150 kW。

(a) 示意图

(b) 实物图
图10给出了上位机界面保存的飞轮充放电切换瞬间的电机d,q电流曲线、直流母线电压曲线、补偿后的d,q电压曲线和飞轮转速测量值。

(a) d,q轴电流曲线

(b) 直流母线电压曲线

(c) d,q轴电压曲线
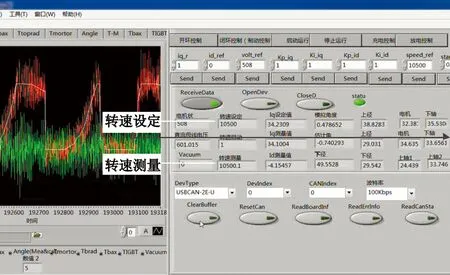
(d) 转速测量值
飞轮稳速10 500 r/min期间,直流母线电压保持600 V(DC),切断电网瞬间,飞轮放电保持直流母线电压500 V(DC)不变(图10(b)中数值508 V(DC)左右,飞轮变流器与UPS之间存在8 V左右压差),可以看出,电压曲线无明显超调和振荡。同时,Id电流基本维持零附近±20 A波动,Iq电流迅速由稳态时的小电流增加至350 A左右,如图10(a)所示,没有出现电流尖峰且电流跟踪特性较好,符合飞轮电池系统的快速放电的要求。同时,在充电稳速阶段,d,q轴电压Vq,Vd与直流母线电压比值在0.6~0.8范围内波动,表明增加补偿后两者幅值基本一致,未加补偿时Vq幅值略大于Vd(图中未标明),此时q轴电压Vq为正值,d轴电压Vd为负值,与式(5)描述内容一致。通过调整转子磁链相位角,使得Vq,Vd幅值接近,可以充分利用转子主磁场。
在放电稳压阶段,Vq幅值由初始较大值逐渐减小,而Vd幅值由初始较小值逐渐增大,在其作用下定子电流开始反向,并不断增大,以维持直流母线电压稳定(Vq与Vd幅值在充电时基本一致,但放电时不同)。由式(4)可知,在充电状态下Vq为正,而Vd为负,在发电状态下Vq的符号取决于负载功率与转速的大小,转速降低,且负向电流iq增大,Vq由较大的正值逐渐降低。在图10(c)中,本文对角度补偿量Δθr的幅值进行了适当的控制,使得Vd的符号逐渐由负值向正值变化,并随转速降低而不断增大。
图11给出了飞轮充放电过程中UPS主控界面显示图。充电时直流母线电压保持600 V(DC)(图11(a)中Bat=600 V),电流幅值从0~40 A(DC)左右调节(图11(a)中为-40.5 A),此时整流器和逆变器均投入工作且高亮显示;放电时UPS整流器已断开且虚线显示,飞轮放电维持直流母线电压500 V(DC)(图11(b)中Bat=500 V),电流保持300 A(DC)左右(图11(b)中为+296 A),表明放电功率维持150 kW,与投入的负载功率相近。采用本文所设计的控制算法,飞轮大功率充放电切换瞬间d,q电流无明显尖峰,Iq,Id电流动态特性较好,进一步提高了飞轮充放电系统的快速性和可靠性。

(a) 飞轮充电稳速

(b) 飞轮放电稳压
4 结 语
本文针对磁悬浮飞轮PMSM的充放电瞬态切换问题展开研究,给出了飞轮工作原理和系统组成,并建立了PMSM三相静止系和两相正交系数学模型,分析了PMSM分别在电动和发电状态下的电压、电流和反电动势的相位关系,通过改变磁链角位置相位实现适当改变磁场强度。根据d,q系转矩电压和励磁电压的关系,提出基于转子磁链相位补偿的充放电切换方法,可有效弥补磁场削弱引入的电流尖峰。实验结果表明,转子磁链相位补偿可使飞轮在大功率充放电切换时取得良好的动态特性,验证了本文方法的有效性,进一步为磁悬浮飞轮电池系统的应用提供可靠基础。

