感应电机磁链与转矩无差拍控制*
李耀华, 陈桂鑫, 王孝宇, 刘子焜, 刘东梅, 任 超
(长安大学 汽车学院,陕西 西安 710064)
0 引 言
有限状态集模型预测控制(FCS-MPC)性能优越、控制灵活,是电机控制领域的研究热点[1-2]。文献[3-5]将模型预测控制应用于感应电机,将逆变器的基本电压矢量遍历代入磁链和转矩预测模型,基于成本函数选择最优电压矢量。模型预测转矩控制(MPTC)选择的电压矢量作用时间固定,可与无差拍控制结合,优化电压矢量作用时间,提高系统性能。文献[6-11]将转矩无差拍控制与MPTC结合,以减小转矩脉动,但该策略仅考虑转矩无差拍控制,磁链控制依然需要模型预测控制,并且系统要进行无差拍控制和模型预测控制,计算量较大。本文提出感应电机磁链和转矩无差拍控制,仿真和实时性试验表明,相比于MPTC和转矩无差拍模型预测控制,所提策略在控制性能和实时性上均具备优越性。
1 感应电机MPTC
静止两相α-β坐标系下,以定子磁链矢量ψs和定子电流矢量is为状态变量,定子电压矢量us为输入变量,三相感应电机状态方程如下:
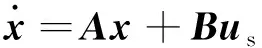
(1)
感应电机转子磁链矢量ψr和电机转矩Te如下:
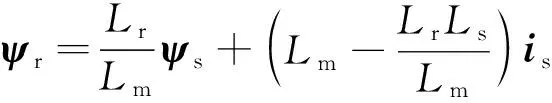
(2)

(3)
采用一阶欧拉向前离散公式对式(1)离散化,则可得下一时刻定子电流矢量和定子磁链矢量预测模型如下:
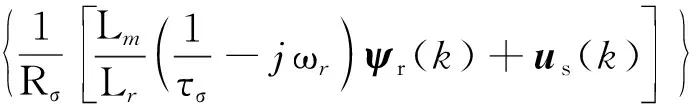
(4)
ψs(k+1)=ψs(k)+Tsus(k)-TsRsis(k)
(5)
将下一时刻定子电流矢量和定子磁链矢量代入式(3),可得下一时刻转矩如下:
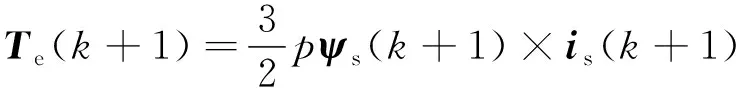
(6)
两电平三相逆变器可产生7个基本电压矢量,如式(7)所示。其中零电压矢量可由000或111两种开关状态生成,具体选择以开关次数最小为原则[12]。
us∈{u0,u1,u2,u3,u4,u5,u6}
(7)
基于当前时刻定子电流矢量、定子磁链矢量和转子磁链矢量,感应电机模型转矩控制系统将逆变器电压矢量遍历代入定子磁链矢量、定子电流矢量和转矩预测模型,则可得到下一时刻定子磁链和转矩。
定义表征磁链和转矩控制性能的成本函数如下所示[13]:
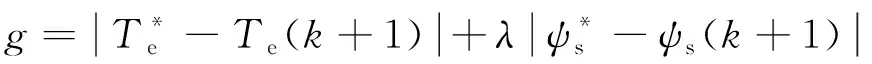
(8)
将磁链和转矩预测值代入式(8),并输出令成本函数最小的电压矢量,从而实现MPTC。感应电机MPTC系统如图1所示。
2 转矩无差拍模型预测控制
由MPTC原理可知,系统通过成本函数定量评价7个电压矢量在一个采样周期对磁链和转矩的控制效果,并从这7个电压矢量中选择相对最优电压矢量,但这只是被动选择相对最优,并未根据系统期望值主动计算绝对最优。因此,可基于转矩误差优化电压矢量作用时间,计算得到理想占空比,实现转矩无差拍控制,从而减小转矩脉动。
将式(3)所示转矩方程对时间求导可得:
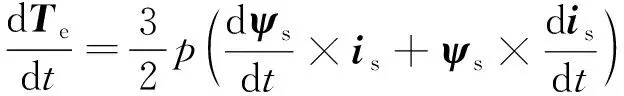
(9)
将式(1)所示的定子电流矢量和定子磁链矢量代入式(9)以替换等号右侧的微分项,并采用一阶欧拉向前公式将等号左侧的转矩导数离散化可得:

(10)
由于au含电压变量,将其作用时间设为tu。对于每个采样时刻,a0为常数项,作用时间设置为Ts,可得:
Te(k+1)-Te(k)=Tsa0+tuau
(11)
根据转矩无差拍原理,可得:

(12)
将当前时刻的转矩参考值近似为下一时刻转矩参考值,可得:
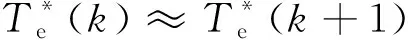
(13)
因此,实现转矩无差拍的电压矢量理想占空比如下:

(14)
将电压矢量遍历代入式(14),则可得到对应的理想占空比。如果计算得到占空比d小于0,表明该电压矢量对转矩的增减效果与无差拍控制相反,应予以舍弃,不进行下一步模型预测控制计算。如果得到占空比d大于1,表明该电压矢量在一个采样周期内无法实现转矩无差拍控制,令占空比为1。这里需要指出:零电压矢量的作用时间必为采样周期,无需转矩无差拍控制计算占空比,直接令d等于1。
由于转矩无差拍控制并未考虑磁链控制,且并不是所有的电压矢量都可实现转矩无差拍控制。因此,需要将占空比调整过的电压矢量代入磁链和转矩预测模型,计算下一时刻的磁链和转矩预测值,通过如式(8)所示的成本函数选择最优的优化电压矢量。
感应电机转矩无差拍模型预测控制系统如图2所示。
3 磁链和转矩无差拍控制
由上文可知,转矩无差拍模型预测控制仅对转矩进行无差拍控制,磁链依然采用模型预测控制,使得磁链脉动较大。因此,下文提出感应电机磁链和转矩无差拍控制。
由式(5)可知,忽略定子电阻压降,定子磁链坐标系下,施加电压矢量us一个采样周期后,下一时刻的定子磁链矢量ψs如图3所示,其中α为施加电压矢量与定子ψs(k+1)磁链矢量的夹角,Δθs为定子磁链矢量角度的变化。
由图3可知,施加电压矢量引起的定子磁链矢量角度变化Δθs如下:

(15)
令q=usTs/ψs,式(15)可简写为

(16)
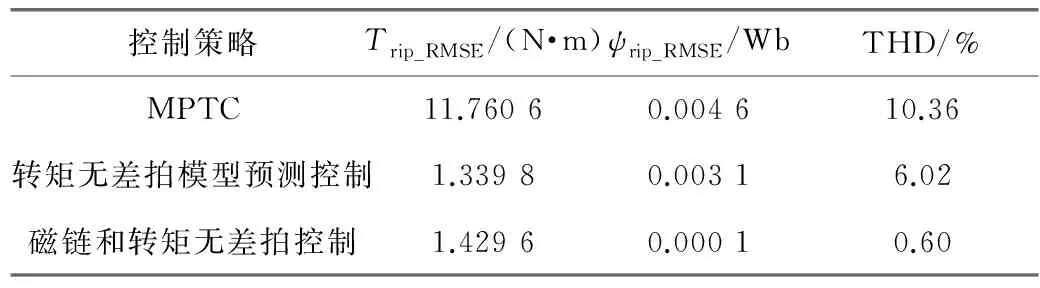
由于采样周期很小,q值较小。当0°<α≤360°、0 由图4和图5可知,此时定子磁链矢量角度的变化较小,cos(Δθs)≈1。因此,下一时刻定子磁链幅值可简化为 ψs(k+1)≈ψs(k+1)cos(Δθs) (17) 由图3可得: ψs(k+1)cos(Δθs)=ψs(k)+usTscosα (18) 设定子磁链矢量与静止坐标系α轴夹角为αψ,施加电压矢量与α轴夹角为αu,则可得: α=αu-αψ (19) 由此可得: usTscosα=usTscos(αu-αψ)= usTs(cosαucosαψ+sinαusinαψ) (20) 电压矢量和定子磁链矢量在静止坐标系α-β轴的分量如下: (21) (22) 将式(20)~式(22)代入式(18),可得: (23) 由磁链无差拍控制可知: (24) 由此可得: (25) 由上文转矩无差拍控制可得: Te(k)+Tsa0+Tsau=Te(k)+Tsa0+ (26) 联立式(25)与式(26),则可求得满足磁链和转矩无差拍控制的理想电压矢量在静止坐标系β轴分量usβ如下: usβ= (27) 将usβ代入式(25),则可求得理想电压矢量在静止坐标系α轴的分量usα如下: (28) 在得到满足磁链和转矩无差拍控制的理想电压矢量后,同样采用空间矢量调试技术生成。感应电机磁链和转矩无差拍控制系统如图6所示。 表1 电机仿真系统参数 感应电机MPTC仿真波形如图7~图10所示。感应电机转矩无差拍模型预测控制仿真波形如图11~图14所示。感应电机磁链和转矩无差拍控制仿真波形如图15~图18所示。 定义转矩脉动均方根误差(RMSE)和磁链脉动RMSE如下: (29) (30) 式中:m为采样个数。 不同控制策略下,0.2~8 s(不含电机软启动)转矩脉动RMSE、磁链脉动RMSE和定子电流总谐波失真(THD)如表2所示。 表2 控制性能 由仿真结果可知: (1) MPTC、转矩无差拍模型预测控制与磁链和转矩无差拍控制下,电机系统均可实现四象限正常运行; (2) 相较于MPTC,转矩无差拍模型预测控制可降低转矩脉动和磁链脉动,转矩脉动RMSE降低88.61%,磁链脉动RMSE降低32.61%,电流THD降低41.89%; (3) 相较于MPTC,磁链和转矩无差拍控制可显著降低转矩脉动和磁链脉动,转矩脉动RMSE降低87.84%,磁链脉动RMSE降低97.83%,电流THD降低94.21%。与转矩无差拍模型预测控制相比,转矩脉动略有增大,但磁链脉动显著降低,磁链脉动RMSE降低96.77%,电流THD降低90.03%。 为了验证不同控制策略的实时性,基于 STM32H7单片机平台对MPTC、转矩无差拍模型预测控制、磁链和转矩无差拍控制进行单步实时性验证。不同控制策略的实时性验证测试用例参数如表3所示。 表3 测试用例参数 对以上3种控制策略进行单步运算循环8万次,不同算法执行时间如表4所示。 表4 算法程序运行时间 由表4可知,MPTC计算耗时最多,转矩无差拍模型预测控制次之,磁链和转矩无差拍控制计算耗时最少,为MPTC的4.79%、转矩无差拍模型预测控制的5.29%。 (1) MPTC、转矩无差拍模型预测控制、磁链和转矩无差拍控制下,感应电机系统均可实现四象限正常运行。 (2) 相比于MPTC和转矩无差拍模型预测控制,磁链和转矩无差拍控制可显著降低转矩脉动和磁链脉动。 (3) 磁链和转矩无差拍控制计算简单,实时性好。与MPTC相比,计算耗时减少95.21%,与转矩无差拍模型预测控制相比,计算耗时减少94.71%。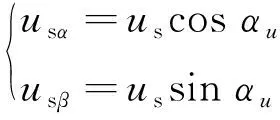
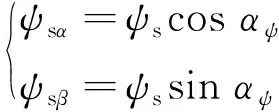


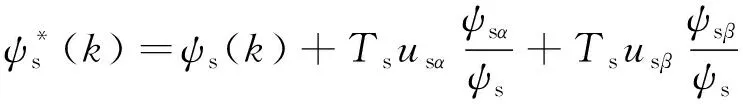
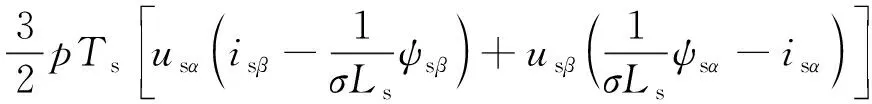
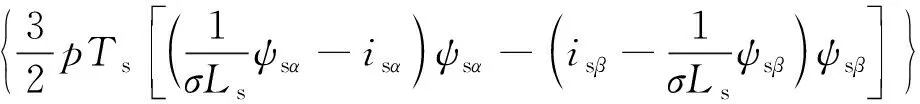
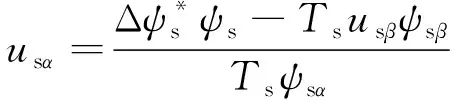
4 仿真验证
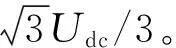

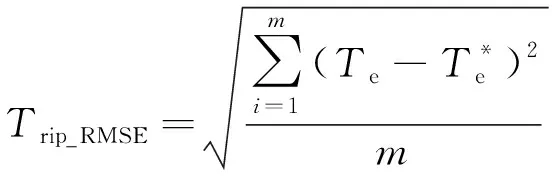
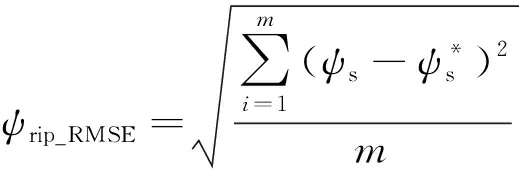
5 实时性验证


6 结 语

