利用负电阻提高电能无线传输功率

朱 静，李华峰，菅 磊

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

0 引 言

无线电能传输(以下简称WPT)作为一种新型的电能传输方式，有效地克服了传统接触式传输方式带来的磨损、火花、污染等一系列缺点[1-3]，因此受到各国学者的广泛关注。

WPT系统的最终目的是用于传输功率，所以它的传输能力一直是研究的重点。目前,常用的提高传输功率的方法有提高输入电压、增加互感、采用新的拓扑结构、改变谐振线圈的相关参数、增大导线线径和电感线圈的半径以及采用多匝导线线圈等[4-5]。文献[6]利用超导材料构成线圈进行WPT,以减少系统损耗,进而实现系统传输功率的提升,也有不少学者对系统谐振拓扑结构进行研究, 希望通过设计不同的补偿拓扑来获得最大的传输功率[7]。

文献[8]研究指出,增多中继线圈匝数，可以有效提高传输功率和增大传输距离。文献[9]针对4种阻抗补偿网络的最大功率传输特性进行了研究，并通过动态调谐控制，实现系统最大功率输出。文献[10]研究指出,当发射回路与接收回路电阻的乘积很小时，使用松耦合谐振才可以获得最大的传输功率，且该结论对于耦合谐振式WPT和电磁共振式WPT均适用。

文献[11]针对磁场共振式WPT系统的等效阻抗及频率、负载和互感系数对系统传输功率的影响进行了分析。文献[12]提出了一种无线电力传输系统，该系统由一个大的矩形线圈和一个带有寄生方形螺旋线圈的小方线环组成，在此基础上，对无线供电系统的谐振频率和功率传输效率进行了数值分析，并研究了接收元件的负载和非共振物体的存在对谐振频率和功率传输效率的影响。文献[13] 实验证明了有效的电力传输可以通过使用两个强耦合的螺旋线圈来实现。

这些研究对提高WPT功率起到了推动作用。然而在一些特定场合，例如对线圈结构参数、传输距离以及输入电压等要求固定的情况下，就无法利用上述方法来提高输出功率。本文在上述方法之外,提出一种提高WPT传输功率的新思路。通过对谐振耦合式WPT传输功率的分析可知，在结构参数、传输距离以及输入电压固定的情况下，减小变压器原边的阻抗，能有效提高系统输出功率。因此在上述研究工作的基础上，本文将谐振耦合式WPT作为研究对象，通过在系统发射回路引入负电阻，来中和线圈阻抗，提高回路电流，从而提高系统输出功率。

1 含有负电阻的谐振耦合式WPT模型

谐振耦合式WPT一般组成如图1所示。电源驱动部分包含供电和高频激磁电路，谐振耦合的频率处在电磁场的中高频频段，此部分功能是将传统电网的工频交流电转化为线圈中的高频电流，用以驱动磁耦合谐振部分产生谐振磁场。磁耦合谐振部分由谐振线圈和电容构成谐振体，发送与接收线圈分别用于产生和接收磁场能量。由于能量采用无线输送形式，且工作频率高于一般用电设备的使用范围，故能量接收和负载电路需将高频电流处理后，以合适的形式供给负载。

图1 谐振耦合式WPT的一般组成

根据系统发射端和接收端进行电容补偿的接入方式不同，电路补偿的拓扑结构可分为4种[14]:串联-串联补偿拓扑(SS)、并联-串联补偿拓扑(PS)、串联-并联补偿拓扑(SP)、并联-并联补偿拓扑(PP)，本文以串联-串联式(SS)系统为研究对象。

SS型谐振耦合式WPT电路模型如图2所示。图2中，US为理想电压源；RS，RD分别为发射、接收线圈的等效电阻；M为两线圈之间的互感；LS，LD为发射、接收线圈的自感；D为两线圈之间的距离；CS，CD为发射线圈和接收线圈的谐振电容；IS，ID为流过发射回路和接收回路的电流；RL为负载电阻。

(a) WPT系统一般等效电路模型

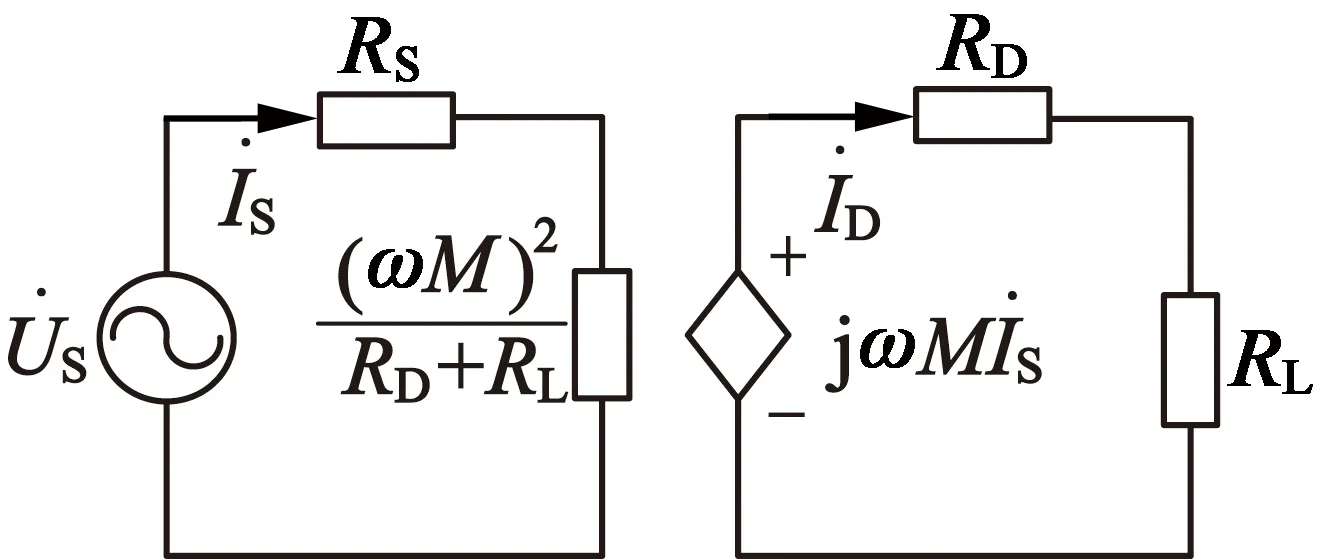
(b) WPT系统原副边分离等效电路模型

当传输系统的发射回路与接收回路谐振频率相同且同为电源角频率时，两回路中电抗为0，此时发射回路自阻抗ZS=RS，接收回路自阻抗ZD=RD+RL。列基尔霍夫定律电路方程可得到回路电流[15]：

(1)

(2)

由式(1)可以看出，在系统形成谐振耦合回路后,发射回路电流不仅仅和自身的阻抗ZS有关,还与(ωM)2/(RD+RL)有关。(ωM)2/(RD+RL)为接收回路对发射回路的反射阻抗，用ZDS表示。反射阻抗ZDS消耗的能量即为发射到接收回路的全部能量，而最终分配到负载上的功率,即输出功率：

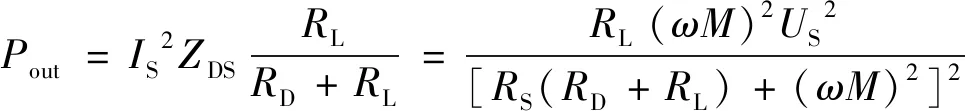
(3)

由式(3)可以看出，反射阻抗ZDS消耗的能量越多，则分配到负载上的功率也就越大，传输功率也就越大。因此，在传输距离以及接收回路参数不变时，反射阻抗ZDS消耗能量多少取决于电流IS的大小。由图2(b)也可以看出，接收回路的电压源大小取决于电流IS。要提高负载上的输出功率，就需要增大发射线圈上的电流IS。然而，在输入电压一定时，要想增大电流，只能通过减小发射回路阻抗来实现。

为此，本文引入负电阻，通过在发射回路中加入负电阻来减小回路阻抗，增大发射线圈上的电流IS，从而提高谐振耦合式WPT系统的输出功率。

图3为含有负电阻的SS型谐振耦合式WPT电路等效模型，其中-RN为负电阻。

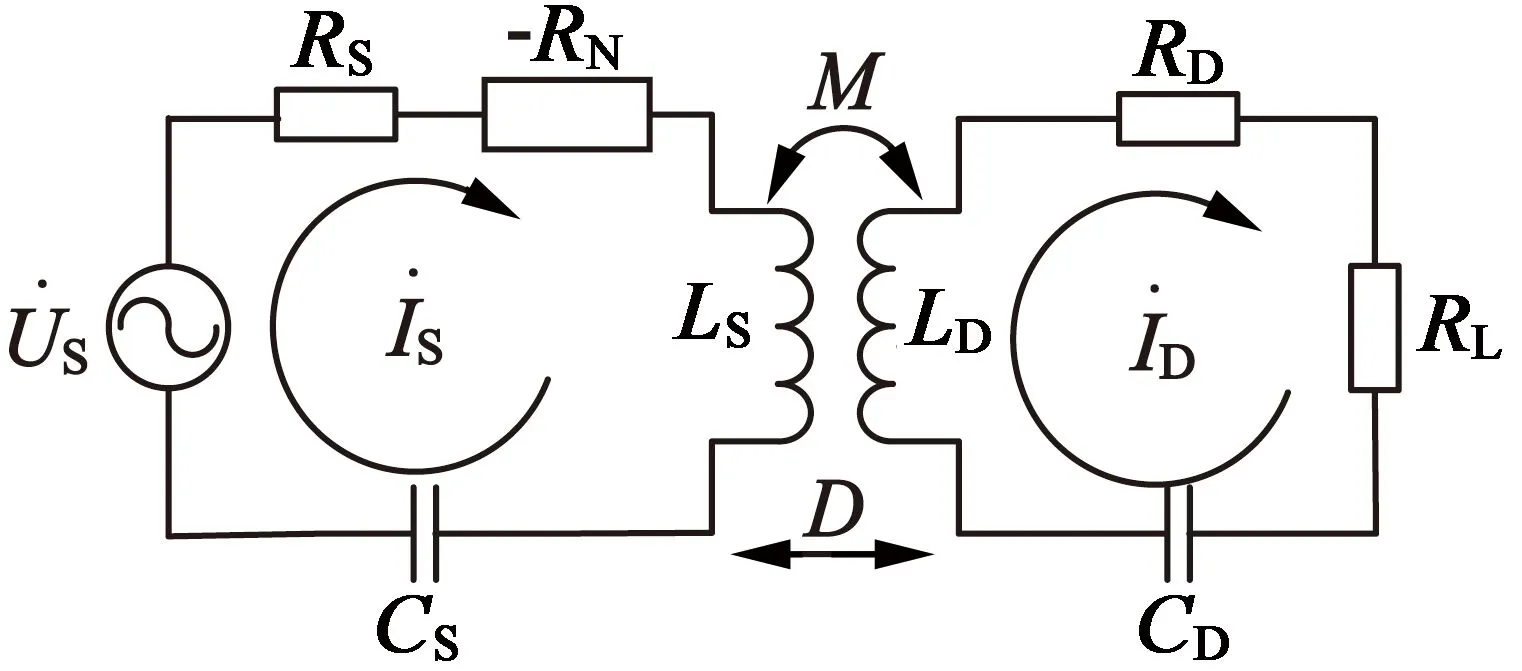
图3 含有负电阻的SS型谐振耦合式WPT等效电路模型

图3发射回路的阻抗ZS=RS-RN,根据式(1)、式(2)、式(3)可知，含有负电阻的谐振耦合式WPT系统两回路的谐振时电流以及负载电阻RL的输出功率Pout如下：

(4)

(5)

(6)

比较式(1)和式(4)、式(3)和式(6)可以看出，利用在发射回路中加入负电阻的方法，确实能够增大发射回路的电流，提高系统的传输功率。为了验证上述理论，下面需要对负电阻进行分析，并进行实验验证。

2 负电阻的原理及组成

负电阻是一种较为特殊的电阻[16]。它满足欧姆定律，但与正电阻不同的是，负电阻是一种有源元件，它并不能单独存在，而是通过其它的电路元件来实现。现有关于负电阻的研究大都还处于理论介绍以及软件仿真阶段[17-18]，有关它在实际工程应用中的研究则较少，但采用类似原理的负电容已在结构振动抑制中得到了成功应用[19]。

常见的负电阻通常由正电阻和运算放大器构成，其电路连接方式如图4所示。

图4 实现负电阻的电路

假设运算放大器工作在线性区，运放两输入端的电压分别为u+和u-，输入端的等效阻抗为Req，则根据运放的“虚短”、“虚断”特性有：

(7)

由式(7)可以得到输入端等效电阻：

(8)

通过合理选择R1，R2和R3的电阻值，即可得到所需要的负电阻。

图5 含有负电阻的谐振耦合式WPT发射回路等效模型

由于负电阻是由运算放大器构成的一种有源元件，必然要受到运算放大器性能的影响，因此，还需要分析负电阻的使用限制条件。

系统副边电路与图3相同。当运算放大器工作在线性区时，结合(4)、式(5)，可列回路方程：

(9)

(10)

为避免电路中加入负电阻过大而使整个回路呈现负阻状态，导致发射线圈上的电流IS流向改变，造成电压源耗能，使整个系统效率更低，则需要发射回路总阻值满足R>0。即：

正如前面所说负电阻是由运算放大器构成的，它的使用必然要受到运算放大器性能的影响，而上述涉及负电阻的电路分析也都是以运算放大器工作在线性区为前提的，也就是说，要形成负电阻，运放必须工作在线性放大状态，而与之对应的运放的输出电流、电压也要限制在运放的正、负饱和区内，即：|IO|≤Isat，|UO|≤Usat。结合式(8)即可得出，为保证含有负电阻的WPT系统正常工作时回路中各电阻以及电源参数的限制范围：

(12)

(13)

(14)

(15)

此外，为保证系统能正常工作，回路中各元器件参数除了要按照上述公式中限制条件进行合理选择之外，还要根据系统的输入信号，考虑运放的带宽以及压摆率等因素。

3 实验验证及分析

本文按照图5的电路设计了一套含有负电阻的串联-串联式结构的谐振耦合式WPT系统，来验证上述理论分析的正确性，实验装置如图6所示。其中发射回路中构成负电阻的运算放大器芯片的型号为OPA541，直流电源给运算放大器芯片供电。信号发生器输出一个高频正弦信号，经过高频功率放大器放大后输出具有一定功率的正弦波，给发射回路供电。

图6 实验装置图

系统的部分参数如下：松耦合变压器线圈匝数n=15，线圈半径r=17 mm,导线半径a=0.54 mm，导线长度l=2.5 m,线圈宽度h=1.68 mm,两线圈之间的距离D=5 mm。线圈电感L=25 μH，谐振电容C=100 nF, 负载电阻RL=100 Ω，系统的串联谐振频率f=100 709 Hz。高频下线圈损耗电阻主要包括欧姆损耗电阻Ro和辐射损耗电阻Rr[13]。

(16)

(17)

式中：μ0为真空磁导率；σ为电导率；ε0为空气介电常数；c为光速。由计算可知：Rr≪Ro≈0。由于线圈的内阻太小，为了得到更加明显的实验效果，本文忽略线圈内阻，在发射回路添加一个100 Ω的电阻作为回路内阻，此时，RS=100 Ω，RD=0。当参数相同的发射线圈与接收线圈同轴放置时，谐振耦合式WPT传输距离与互感的关系:

(18)

将参数代入式(18)，得到两线圈之间的互感M≈1.97×10-5H。

实验系统中,高频功率放大器输出电压US的峰峰值为20 V，通过在回路中加入不同大小的负电阻，测得发射线圈上的电流IS(峰峰值)和负载RL上的电压UL(峰峰值)如图7所示。其中电流IS是由2 mA/mV的比例交流电流探头测得。

(a) -RN= 0

(b)RN= 10 Ω

(c)RN= 20 Ω

(d)RN= 30 Ω

(e)RN= 40 Ω

(f)RN= 50 Ω

(g)RN= 60 Ω

图7不同负电阻下电流IS和电压UL

根据图7中测得的数据，计算出负载上电压有效值UL，进而算出系统实际输出功率Pout=UL2/RL。将系统各元件参数代入式(4)和式(6)中，对发射回路电流IS以及功率Pout进行理论计算，最终得到实验值与理论值的对比结果，如图8和图9所示。

图8 不同负电阻下发射线圈电流

图9 不同负电阻下系统的输出功率

由图9可以看出，与不加负电阻的情况相比，在系统中引入负电阻确实提高了系统的输出功率，而且输出功率最大提高了将近6倍，效果显著。

上述数据中，实验值与理论值存在一定的差异，由于理论计算时忽略了高频下空心线圈的寄生电感、电容等因素，理论计算出的谐振频率不一定是系统的实际谐振频率，系统含有电抗成分，导致发射回路实际电流偏小。忽略这些误差，理论值和实验值具有较好的一致性。

4 系统效能比的分析

本文系统中输出功率之所以能够得到提高，是由于在发射回路中加入了负电阻，而负电阻又是一种由运算放大器构成的有源元件。因此，系统中输出功率增大的那部分能量ΔPout主要来源于两部分，一部分来源于给负电组供电的直流电源提供的能量ΔPin1，另一部分来源于发射回路电流增加ΔIS而导致交流电压源US多提供的能量ΔPin2。定义效能比ρ=ΔPout/(ΔPin1+ΔPin2),用以评价负载上增加的功率与系统原边多提供的功率之间关系。

实验中给运算放大器提供正负电压的直流电压源VCC=-VEE=30 V，正负电源电流ICC，IEE。由于系统两回路处在串联谐振状态，回路中电抗为0，因此，电路可近似看作为纯阻性。结合运算放大器的结构，可近似认为：IO=IS+IP≈|ICC|+|IEE|，由此可得到：

ΔPin1=VCCICC+|VEE||IEE|=VCC(IS+IP)

(19)

ΔPin2=ΔISUS

(20)

(21)

由图4可知，对于某一个固定阻值的负电阻，在满足系统正常工作的前提下，组成负电阻的各正电阻的阻值是不固定的，有多种匹配方式。但不同的电阻匹配方式得到回路中的电流却不相同。因此，当在系统中加入固定阻值的负电阻时，就要考虑选用何种电阻匹配方式，使系统效能比尽可能大。

由式(4)和式(6)可知，发射回路的电流以及输出功率的大小与加入的负电阻的大小有关，与其如何构成无关。因此，当负电阻的阻值一定时，系统输出功率的增量ΔPout以及发射回路电流增量ΔIS也是固定的，为了提高效能比，就需要尽可能减小ΔPin1,即减小电流IP。由式(10)中电流IP的计算公式可知，要减小电流IP就需要增大电阻R3。

为了验证这一理论分析的正确性，本文利用图6实验装置，进行了5组实验，其中负电阻的结构参数：-RN=-50 Ω，RS=100 Ω，R1=50 Ω，R2=R3，实验结果如图10所示。

图10 不同R3下系统的效能比

图10的实验结果表明，在保持负电阻大小不变时，增大R3，确实能够减小电流IP，提高系统效能比。

5 结 语

本文以串联-串联式结构的谐振耦合式WPT系统为模型，推导了含有负电阻的WPT系统电路中各回路电压、电流以及输出功率的表达式，同时给出了为保持系统中负电阻能正常工作时各元器件参数的选择范围，并通过效能比概念分析了为获得一定的输出功率提高，如何选择负电阻参数以减小输入损耗。实验结果表明，利用负电阻能够减小WPT系统回路中的阻抗，增大回路电流，从而提高系统的输出功率。同时，也验证了提高系统效能比的方法。本文的方法是对目前已有提高谐振耦合式WPT系统输出功率各种方法的有益补充，具有较好的指导意义，并在某些特定场合，例如提高电源的输出功率等场合也具有良好的适用性。