一种纵弯复合单驱动足超声波电动机的设计
张斯阳
(湖北大学知行学院, 武汉 430011)
0 引 言
超声波电动机是近几十年成长的非典型特种微电机,它既没有传统电动机的磁极,也没有电磁感应的过程,超声波电动机主要运用的是压电材料的逆压电效应,让输入的电能转化为输出所需的机械能[1]、输出功率、驱动负载[1-2]。
1 纵弯复合超声波电动机理论分析
1.1 结构设计
本文研究了一种新型的纵弯复合单驱动足超声波电动机,该电机的结构如图1所示。该超声波电动机由后端盖、法兰螺栓、法兰盘、变幅杆、压电振子、电极、驱动足以及摩擦片组成。法兰螺栓连接后端盖与压电振子以及变幅杆,法兰盘两侧有两个锥孔,是两个夹持点,用于固定电机。两个变幅杆的小端与驱动足相连接,驱动足输出位移,驱动足贴有摩擦片。

图1 电机结构示意图
图2为电机压电振子位置选择、极化方向以及电路连接情况。两对纵振压电振子在d33模式下工作,每对纵振压电振子中的每片纵振压电振子的极化方向相反,每片纵振压电振子的极化方向与关于驱动足相对称的纵振压电振子的极化方向相同,每片纵振压电振子均置于纵振振型的节点处,从而保证一组压电振子在收缩状态时,另一组压电振子处于伸长状态,实现驱动足的推拉谐振运动[3]。两对弯振压电振子在d31模式下工作,每对弯振压电振子的极化方向相同,每片弯振压电振子的极化方向与关于驱动足相对称的弯振压电振子的极化方向相同,每片弯振压电振子均置于电机振型的波腹处。

图2 压电振子的极化方向布置与接线情况
1.2 工作原理
1.2.1 驱动足的运动轨迹分析
如图3所示,在驱动足与动子相接触的一侧取面中心O,在压电振子的激励下,定子产生纵向振动与弯曲振动的响应,驱动足分别在Y轴和X轴的方向上进行简谐振动,则点O在Y轴和X轴的方向上的位移y和x分别如下:
(1)
式中:W1为驱动足在Y向上的振动幅值;W2为驱动足在X向上的振动幅值;α为Y向上的振动初始相位;β为X向上的振动初始相位;ω为超声波电动机的谐振频率。

图3 驱动面的中心
对式(1)进行三角变换,可得:
(2)
从式(2)可以看出,中心O在XOY平面内的运动轨迹为椭圆,且椭圆的中心即为O的静止点。电机所受的两相激励电压的相位差β-α决定了轨迹椭圆主轴的方向。分别令相位差β-α如下:

(3)
可得中心O的运动轨迹如图4所示。

图4 不同相位差下中心O的运动轨迹
图4表明,通过具有一定相位差的纵振和弯振组合,驱动足可以实现以椭圆轨迹运动的激励,纵振和弯振的振幅与相位差决定了椭圆轨迹的主轴长度和主轴方向。
当β-α=π/2时,式(2)简化:
(4)
式(4)表明,对于弯振超声波电动机,当两相激励电压之间的相位角为π/2时,其驱动面中心O点在XOY平面内的运动轨迹为主轴的方向分别为OY和OX方向的椭圆,且W1和W2分别为椭圆主轴的长度,我们可以通过调整两相激励交变电压的幅值来调整椭圆轨迹主轴长度。
1.2.2 电机的运动机理分析
给纵振压电振子加载sin(2πft)(f为纵弯简并后的谐振频率)的交流电压,给弯振压电振子加载cos(2πft)的交流电压。纵振压电振子在d33的工作模式下激励电机的纵振模态,弯振压电振子在d31的工作模式下激励电机的弯振模态,纵振模态和弯曲模态相叠加,驱动足的运动轨迹呈椭圆。若将加载的两相交流电压的相位差改为-π/2,电机可以实现反向驱动。电机在一个周期内的振型变化如图5所示。

图5 电机在一个周期内的振型变化
2 纵弯复合超声波电动机结构设计
2.1 模型的建立
本文设计的纵弯复合单驱动足超声波电动机选用的压电材料为PZT-5H,变幅杆、驱动足以及法兰盘均选择硬铝合金,后端盖的材料选择45#钢。图6为在ANSYS中建立的纵弯复合单驱动足超声波电动机的有限元模型。

图6 电机的有限元模型
2.2 结构参数灵敏度分析
纵弯复合单驱动足超声波电动机的结构参数对电机的纵振、弯振频率均有影响,但不同的参数对频率的影响效果不同。本文采用有限元进行分析,通过数据和图形的对比,找出不同参数对纵振以及弯振谐振频率的灵敏度。图7为标注了结构尺寸的电机[3-6]。

图7 电机的尺寸标注
从图7可以看出,电机的主要结构参数有:L1为变幅杆的长度,L2为变幅杆基座长度,tp为压电振子的厚度,L3为法兰盘厚度,L4为后端盖长度;压电振子、法兰盘和后端的横截面尺寸一致,宽度为A2,厚度为B2,驱动足的宽度为q1,变幅杆宽度变化系数为η,变幅杆厚度变化系数为ξ。初始结构参数如表1所示。

表1 初始结构参数/mm
将表1中的初始结构参数输入ANSYS,建立电机有限元模型,将电极面上的节点耦合,模型加载电压后对电极进行短路处理。对电机进行模态分析,得到电机的一阶纵振模态和五阶弯振模态分别如图8和图9所示。

图8 一阶纵振模态

图9 五阶弯振模态
经过对有限元模型的计算,在初始结构参数条件下,一阶纵振频率为31 242Hz,五阶弯振频率为36 395Hz,频率差值为5 153Hz。可见,在初始参数条件下,纵振弯振的频率差值较大,需要对模型的结构参数进行优化,使频率差值尽量接近。
通过有限元分析,得出各参数对谐振频率的影响,如图10所示。

(a) L1

(b) η

(c) ξ

(d) L2
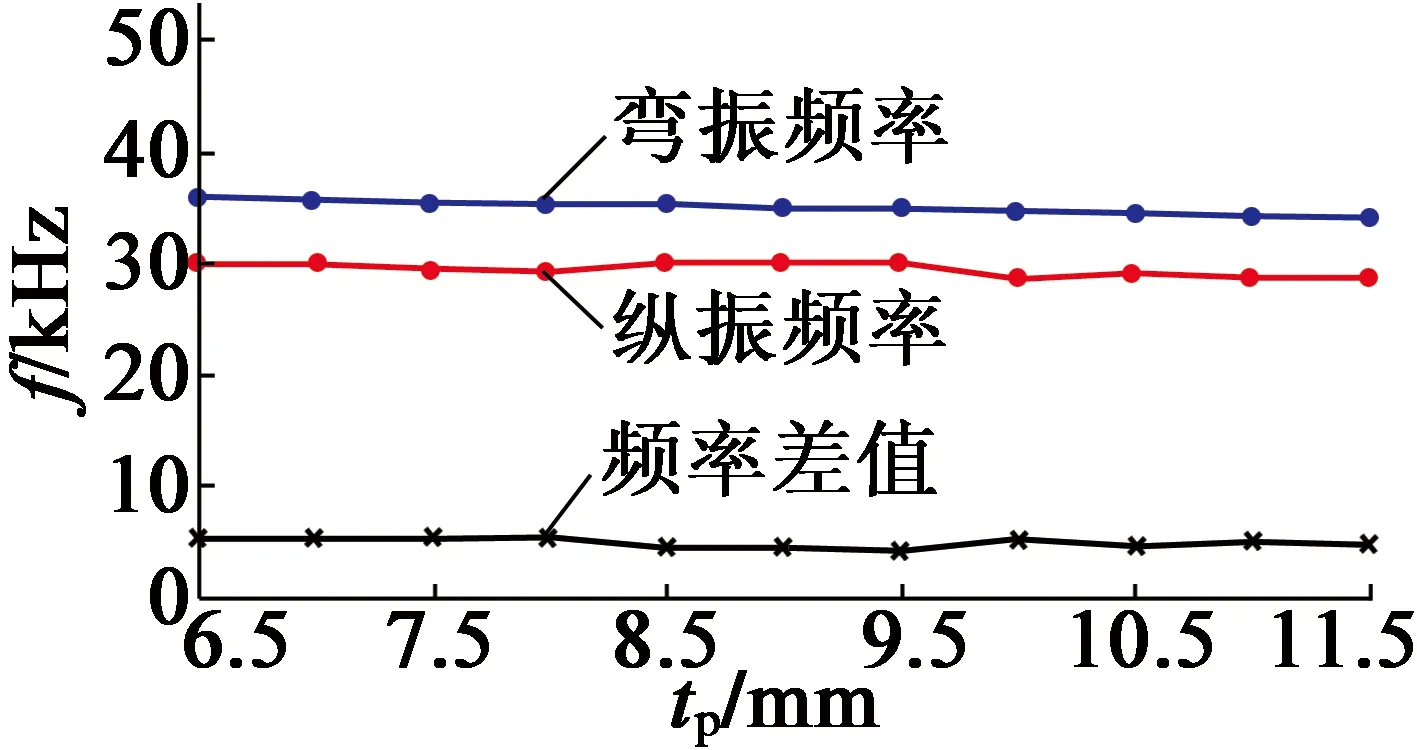
(e) tp

(f) L3

(g) L4

(h) A2

(i) B2

(j) q1
图10各参数对谐振频率的影响
2.3 纵弯模态简并
根据上述分析,了解到各个结构参数对纵弯超声波电动机各阶谐振频率的影响。首先调整10个结构参数,使一阶纵振频率与五阶弯振频率尽量接近;再微调变幅杆的各个系数,找到能使纵振频率和弯振频率最为接近的系数;并保证其谐振频率在超声波频率以上,以避免超声波电动机产生噪声。其中,法兰盘厚度L3为5.5mm和6.5mm时,一阶纵振模态出现纵振和扭振模态,不可取。优化后的结构尺寸参数如表2所示。

表2 优化后结构参数/mm
建立优化参数后的纵弯超声波电动机有限元模型,在ANSYS中实现模态分析,可得其一阶纵振频率为26 435 Hz,五阶弯振频率为26 507 Hz,频率差值变为73 Hz。纵振模态和弯振模态如图11所示,基本实现了纵弯模态简并。特别强调的是,在优化参数的过程中,纵振压电振子位于纵振的节点位置,弯振压电振子位于弯振的波峰/波谷处,使纵向振动和弯曲振动的激励充分利用。法兰盘位于弯振的节点处,可尽量约束对激励的影响。

(a) 一阶纵振模态

(b) 五阶弯振模态
3 结 语
本文设计了一款新型的将压电材料d31和d33相结合的纵弯复合单驱动足超声波电动机,确定了其压电振子的分布以及极化方向,设计了超声波电动机的电路连接方式。对纵弯复合单驱动足超声波电动机的10个结构参数进行了灵敏度分析,得到不同参数对电机的纵振模态、弯振模态以及频率差值的影响,并进行了纵弯简并,得到了理想的结构参数。

