基于自适应滑窗的开关磁阻电机调速系统故障诊断

杨文浩，苟 斌，雷 渝，宋潇潇，王 军

(1.西华大学 电气与电子信息学院，成都 610039；2.四川省电力电子节能技术与装备高校重点实验室，成都 610039)

0 引 言

开关磁阻电机调速系统(以下简称SRD)具有结构简单、容错力强、运行高效等优点，被广泛应用于航空航天、轨道交通等领域[1]。但SRD中功率变换器的绝缘栅双极型晶体管(以下简称IGBT)和传感器在实际运行中易发生故障[2-5]。IGBT短路、开路故障，传感器噪声、卡死等故障，会导致电机失速或工作在不平衡状态，甚至会造成SRD瘫痪。因此，SRD中功率变换器IGBT和传感器故障的快速诊断、精确定位成为专家学者的研究热点。

目前，国内外专家学者对电机调速系统的故障诊断方法主要有基于模型、基于信号、基于数据三类[6]。基于模型的故障诊断方法，通过建立数学模型实现对故障的在线诊断[7-10]。文献[7]通过测量直流母线电流和续流总线电流，建立逻辑诊断模型。该方法能够在几个PWM周期内诊断故障，但是增加了系统逻辑复杂度。文献[9]通过公式推导与数学分析，建立双馈异步发电机的多回路数学模型，计算转子平均瞬时功率实现匝间短路故障诊断。基于信号的故障诊断方法，通常需要增加额外的传感器对特征信号进行采集，来实现故障诊断[11-14]。文献[11]将高频电压信号注入功率变换器，通过分析采集的三相电流频率和幅值，实现对故障的诊断。该方法虽不用增加额外的传感器，但因高频信号的注入，电机将会产生噪声和附加损耗。文献[13]通过检测定子电流信号和振动信号实现对定子绕组和滚子轴承的故障诊断。该方法额外增加了3个振动传感器，系统成本随之提高。基于数据驱动的方法，诊断速度快且精度高，但需要离线训练及参数调试[15-20]。文献[15]通过小波分析与支持向量机，实现功率变换器IGBT故障诊断，但需要复杂的数据处理与离线训练。

分析基于模型、基于信号、基于数据三种方法的优缺点，为了使基于数据驱动的故障诊断方法离线处理速度快，简化参数调试过程，本文将k-近邻算法(以下简称kNN)与极限学习机(以下简称ELM)算法相结合，提出了一种基于自适应滑窗的故障诊断方法。kNN算法分类精度高，易于实现，不需要离线训练，但是在近邻距离较大时，计算复杂，响应速度较慢。ELM离线训练和在线分类速度快、精度高，其结合kNN算法不但能够相互补偿提高精度，还能提高诊断系统的响应速度，避免复杂的参数调试过程。该方法通过快速傅里叶变换(以下简称FFT)对事先获取的开关磁阻电机原始数据进行特征提取，并利用特征选择算法ReliefF降低特征数据维数。通过kNN及集成ELM形成自适应滑窗诊断机制，从而实现对SRD故障的快速诊断。通过MATLAB/Simulink离线和在线仿真实验，验证了该方法的有效性。

1 SRD故障类型

本文以使用三相不对称功率变换器的12/8极SRD作为研究对象，SRD如图1所示。

图1 SRD框图

IGBT故障分为短路故障和开路故障两类。当功率变换器一相单个IGBT发生开路故障时，该相将不会继续产生励磁，通常有硬件保护采取相应措施，避免发生二次故障。当功率变换器一相单个IGBT发生短路故障时，整个驱动系统仍保持运行，因此，短路故障是一种潜在故障。此时，故障相仍能产生励磁，但故障相电流将会大幅增加，产生大量热量，长时间运行在这种状态可能导致系统崩溃。所以，本文主要针对单个IGBT短路故障。A相单个IGBT故障时，A相电流如图2所示。

(a) A相单管开路故障电流

(b) A相单管短路故障电流

图2A相单个IGBT故障电流

传感器故障通常分为噪声、卡死、偏移三种类型，分别由式(1)、式(2)、式(3)表示。

(1)

(2)

(3)

式中：y1(t)，y2(t)，y3(t)分别为传感器噪声、卡死、偏移故障输出；yn(t)为传感器正常输出值；Δφ(t)为白噪声；C(t)和C1(t)为故障下的恒定值；t0为故障发生时刻。

在实际运行过程中，传感器受环境、使用年限等影响，常出现噪声故障。电流传感器发生噪声故障时，系统将产生大量谐波并发热，使系统工作在不平衡状态下，导致电磁转矩和电机转速出现波动。而转速传感器的噪声故障将会影响系统的控制策略，导致控制效果不佳，电机转速无法保持恒定。传感器发生噪声故障时，A相电流如图3所示。

(a) 转速传感器噪声故障

(b) A相电流传感器噪声故障

图3传感器故障A相电流

本文主要诊断的SRD故障类型及故障标签设置如表1所示。

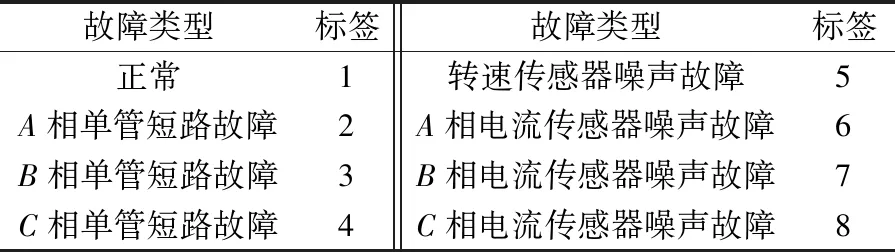
表1 SRD故障标签

2 故障诊断方法

本文的方法分为离线数据处理和在线故障诊断两个部分。故障诊断结构如图4所示。

离线数据处理部分通过三相电流传感器获取三相电流作为原始数据，对不同故障下的数据设置标签进行区分。本文采用FFT对原始数据进行谐波分析提取故障特征，对多个特征量的主要谐波成分的幅值连接起来并进行标准化处理，并通过ReliefF算法对数据进行特征选择，降低数据维数，便于集成ELM和kNN训练。

在线故障诊断部分有3个窗口。窗口1，通过kNN和集成ELM分类器1对数据进行分类，如若两种算法分类结果一致，则认为该分类结果可靠，否则不可靠，不可靠数据滑动进入窗口2；窗口2，通过集成ELM分类器2对窗口1不可靠数据进行分类，根据分类规则，不可靠数据滑动进入窗口3；窗口3，对上一窗不可靠数据经过kNN进行全分类，得到分类结果，至此，所有故障数据将被诊断完成，得到分类结果。

图4 故障诊断结构图

2.1 快速傅里叶变换

FFT算法利用了数字信号在时间域的卷积操作等价于频率域的乘法操作的性质，避免离散傅里叶变换(以下简称DFT)中相同多项式的重复计算，有效提高了计算速度。DFT可以表示：

(4)

FFT则是将DFT多项式中奇数项与偶数项分别表示：

(5)

式中：

奇数项与偶数项多项式相同，符号不同，避免了重复计算。由于传感器噪声故障会产生大量谐波，故本文采用FFT算法分析三相电流数据谐波频谱特性，用以区分故障类型。

2.2 ReliefF特征选择算法

ReliefF是二分类特征选择Relief算法扩展用于多分类特征选择的算法。ReliefF算法每次从训练样本集中随机取出一个样本R，然后从和R同类的样本集中找出R的k个近邻样本Hj，从每个R的不同类的样本集中均找出k个近邻样本Mj(C)，根据下式得到特征权重。

式中：diff(A，R1，R2)表示样本R1，R2在特征A上的差。

2.3 kNN算法

kNN算法是一种惰性算法，不需要离线训练模型，并且诊断速度快，通常仅需要调试近邻距离和距离算法这两个参数。该算法分类原理是通过寻找测试样本在训练集最类似的k个样本，并通过设置好的分类规则对k个类似样本进行处理，从而得到最终分类结果。常见的距离计算法包括：

1) cityblock：

(7)

2) euclidean：

(8)

3) hamming：仅用于字符串，两个等长度字符串相对位置上不同字符串的个数。

4) cosine：通过测量两个夹角的度数来度量两者之间的相似度，夹角度数0则相似度为1，180°则相似度为-1。

2.4 ELM算法

ELM是一种具有随机性的快速学习算法，ELM在计算时初始化输入权重和偏置，并得到响应的输出权重，正是这种随机性使得ELM适用于数据量较大的情况。ELM在使用时仅需要调节隐藏层数目、激活函数等参数。

对于有N个样本的L层神经网络，样本：

Xi=[xi1,xi2,…,xin]T

ti=[ti1,ti2,…，tin]T

其网络可以表示：

(9)

式中：g(x)为激活函数；Wi为输入权重；βi为输出权重；bi为隐层单元的偏置。

但隐层神经网络的最终目的是输出尽可能得小，可以表示：

(10)

式中：oj为实际输出；tj为期望输出。

根据式(6)和式(7)，L层神经网络存在：

(11)

简化式(11)，根据矩阵表示:

Hβ=T

(12)

式中：H表示隐层节点的输出，也即激活函数的输出；T为期望的输出；β为输出权重。

由于H是由激活函数得到，一旦输入权重和偏置随机确定，设定好激活函数后，输出权重也就确定，式(12)可以改写如下：

β=H-1T

(13)

式中：H-1为H的Moore-Penrose广义逆矩阵。

ELM已经被广泛应用于分类和拟合问题中，相对于传统的方法，这种算法训练速度更快，调试参数更少。传统的ELM在分类问题中仅用于二分类问题，对于本文的多故障分类，需要采用多分类ELM。

2.5 多分类ELM

根据式(11)和式(12)能够得到：

(14)

式中：h(x)=[h1(x),h2(x),…,hL(x)]为隐藏层的输出矢量；β=[β1(x),β2(x),…,βL(x)]T为隐藏层节点的输出权重；h(x)实质上就是输入数据到特征空间H上的映射。

对于二分类器，其决策函数：

f(x)=sign[h(x)β]

(15)

对于二分类问题，ELM仅使用单个输出节点，并将其输出值最接近的类别作为输入数据的预测类别。对于多分类问题，目前使用的方法有两种：

1) 采用单输出多分类：即ELM仅采用单个输出节点，但有多个类别，输出值最接近的类别被选作为输入数据的预测类别。能够看出，此时二分类问题是单输出多分类器的一种特殊情况。

2) 采用多输出多分类：即ELM采用多个输出节点，并将多个输出节点的最大输出所最接近的类别作为输入数据的预测类别。m个节点的输出值矢量应为f(x)=[f1(x),f2(x),…,fm(x)],这时其决策函数可以写为：

(16)

2.6 集成ELM

由于ELM具有随机性，会导致在相同输入情况下输出可能会有所不同。但正是因为这种随机性，可以对多个分类器进行训练构成集成分类器，从而提高分类精度。

2.6.1 学习过程

对于单个ELM分类器，它们随机输入权重和偏置。对于集成ELM，每一个ELM分类器间相互补偿，从而减小误差提高分类精度。本文所采用的集成ELM学习过程表示如下。

对于一个包含E个单个ELM分类器的集成分类器，共D组数据，每组数据特征个数F个，即F×D。

1)随机从D组数据中取出d组数据。

2)在隐藏层数目优化范围内随机取得隐藏层个数及激活函数。

3)训练分类器

2.6.2 分类规则

对于两个相似的样本，输出节点的值将会非常接近。这时，运用前文所描述的分类规则，通常误诊断率相对较高。本文提出一种分类规则，这种分类规则既能准确地判断数据分类结果的可靠性，又能与kNN算法相互补偿。

对于集成分类器1，包含E个单个ELM分类器的集成分类器，共D组数据，每组数据特征个数F个，即F×D。规则如下：

1) 单个ELM分类类别即输出节点的最大值所预测的类别。

2) 集成ELM分类器预测类别即单个ELM分类器预测类别最大相同数目所预测的类别。

3) 数据全分类。

集成分类器1分类结果与kNN分类结果进行比较，若相同，则认为是第一窗分类结果；若不同，则认为分类不可靠，将滑动到下一窗。

对于集成分类器2，包含E个单个ELM分类器的集成分类器，共D组数据，每组数据特征个数F个，即F×D。规则如下：

1) 单个ELM输出节点的最大与第二大输出值之差大于某个阈值，且最大的输出值大于某个阈值，则认为是预测类别，即：

f1(x)>f2(x)>…>fi(x)

iff1(x)-f2(x)>oandf1(x)>p

式中：p，o为使用者所设定的判断单个ELM分类是否可靠的阈值。

2) 集成ELM分类器认为E个单个ELM分类器的预测类别最多的与第二多的之差大于某阈值，且第二大的预测数目不为0，则认为预测类别为最多数目所属类别，否则认为数据不可靠，即:

am>an>…>av

ifam-an>qandan≠0

式中：q为使用者所设定的判断集成ELM分类器预测结果是否可靠的阈值。

E个ELM分类器分类结果如表2所示。

表2 ELM分类结果

表2中，a1+a2+…+a8=E。

3 离线仿真验证

3.1 数据获取

本文以三相12/8开关磁阻电机作为研究对象，电机模型参数如表3所示。在MATLAB/Simulink中搭建SRD仿真模型，模型包括开关磁阻电机、三相不对称功率变换器、电流硬斩波控制策略模块。Simulink仿真如图5所示。

图5 Simulink仿真结构

电机参数数值电机参数数值相数(极数)3(12/8)额定转速ne/(r·min-1)1000额定转矩Te/(N·m)106额定功率Pe/kW11定子内径Φsi/mm164转子内径Φri/mm60定子外径Φso/mm260转子外径Φro/mm163定子轭高hes/mm15转子轭高her/mm24定子极弧/mm0.5转子极弧/mm0.355定子铁心长ls/mm210硅钢片叠压系数0.95

开关磁阻电机采用电流斩波控制方式时，功率变换器每相两个IGBT在运行过程中同时开通或同时关断。因此，无论是上管短路还是下管短路，将会对系统产生相同的影响。本文以上管短路为例，对单管故障进行诊断，由于三相功率变换器各相相互独立并具有对称性，为了避免拓扑结构的对称性导致电流波形类似，特征量特征不明显，并且不增加SRD中所使用的传感器，本文选用ia-ib，ib-ic，ia-ic三个特征量作为故障诊断依据。通过FFT对电流数据进行谐波分析，ReliefF算法选择权重占比较大的特征作为诊断依据，能够得到如图6所示故障特征。当各相单个IGBT短路、转速传感器故障、各相电流传感器发生噪声故障时，所提取的特征波形具有明显的区分度。

(a) 正常特征

(b) A相单管短路故障特征

(c) 转速传感器噪声故障特征

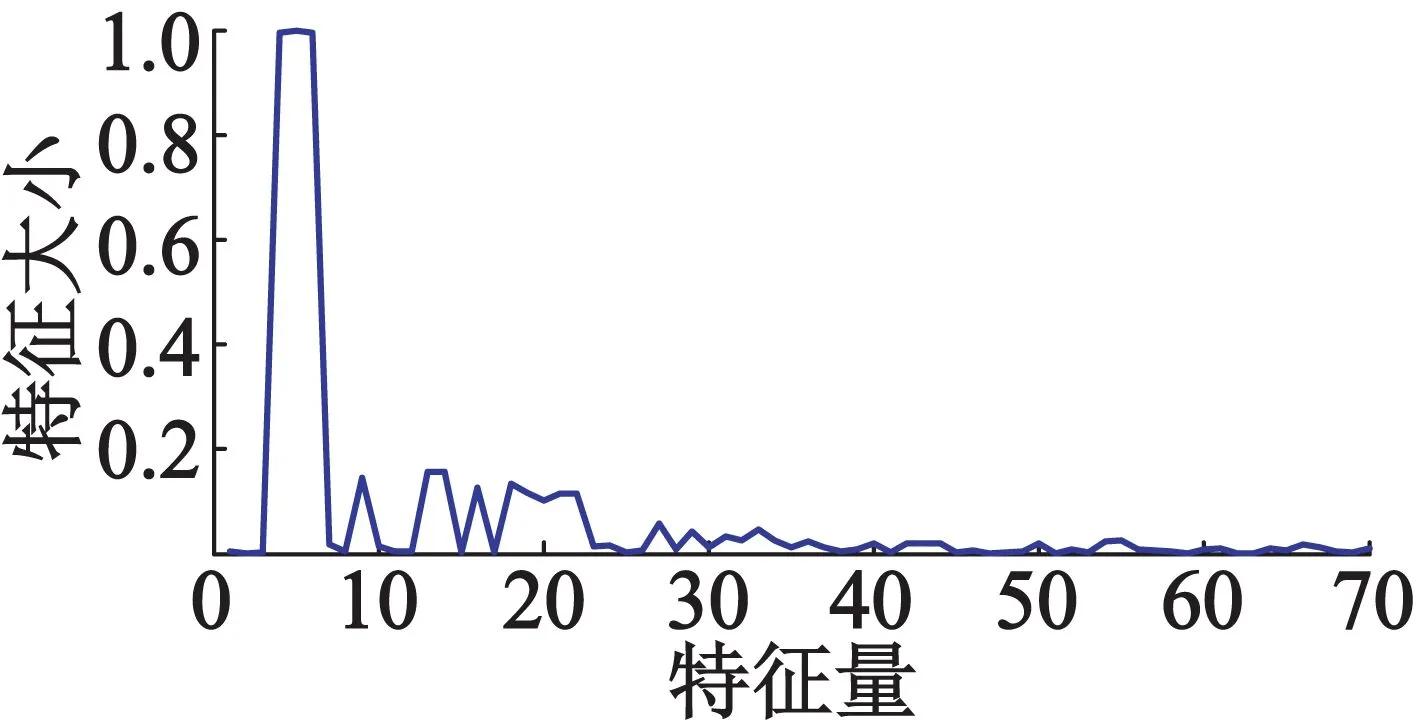
(d) A相电流传感器噪声故障特征

图6故障特征

为了证明本文的故障诊断方法的可靠性，原始数据在不同负载、不同转速下进行采集。本文的开关磁阻电机模型额定转速为1 000 r/min，额定负载转矩110 N·m。数据采集过程中，电机转速由400 r/min每间隔2.5 r/min增加到1 000 r/min，负载转矩由0每间隔0.5 N·m增加到120 N·m，确保原始数据集包含低速到高速、空载到过载，每种故障采集482组数据，因此，7种故障和正常状态下共有3 856组数据。其中20%的数据用于测试，80%数据用于训练，所以有771组数据用于测试，3 085组数据用于训练。

3.2 参数调试

根据前文分析可知，kNN算法与ELM算法仅需要调试较少的参数。kNN算法通常只需要调试它的近邻距离以及距离计算方法。近邻距离在[1,20]间进行寻优，距离计算方法中hamming法仅适用于二分类问题，因此在本文中不适用。如图7所示，在采用近邻距离在[1，2]这个范围内三种距离计算方法的分类精度都较高，在距离为1和2两个点时，cityblock距离计算方法分类精度达到了98.70%，因此，本文选择采用邻近距离为1，距离计算方法为cityblock。

图7 kNN参数优化图

ELM参数仅需要调试激活函数类型、隐藏层数目。在全部原始数据中随机选取80%作为训练数据，20%作为测试数据。在不同激活函数和不同隐藏层数目下，hardlim作为激活函数时，分类精度不稳定，如图8所示，其余4种作为激活函数时能够在[300，500]区间内获得最大分类精度，且在局部区间内sigmod作为激活函数时能够获得最大精度97.80%。因此，本文选取sigmod作为激活函数，隐藏层最优范围为[300，500]。

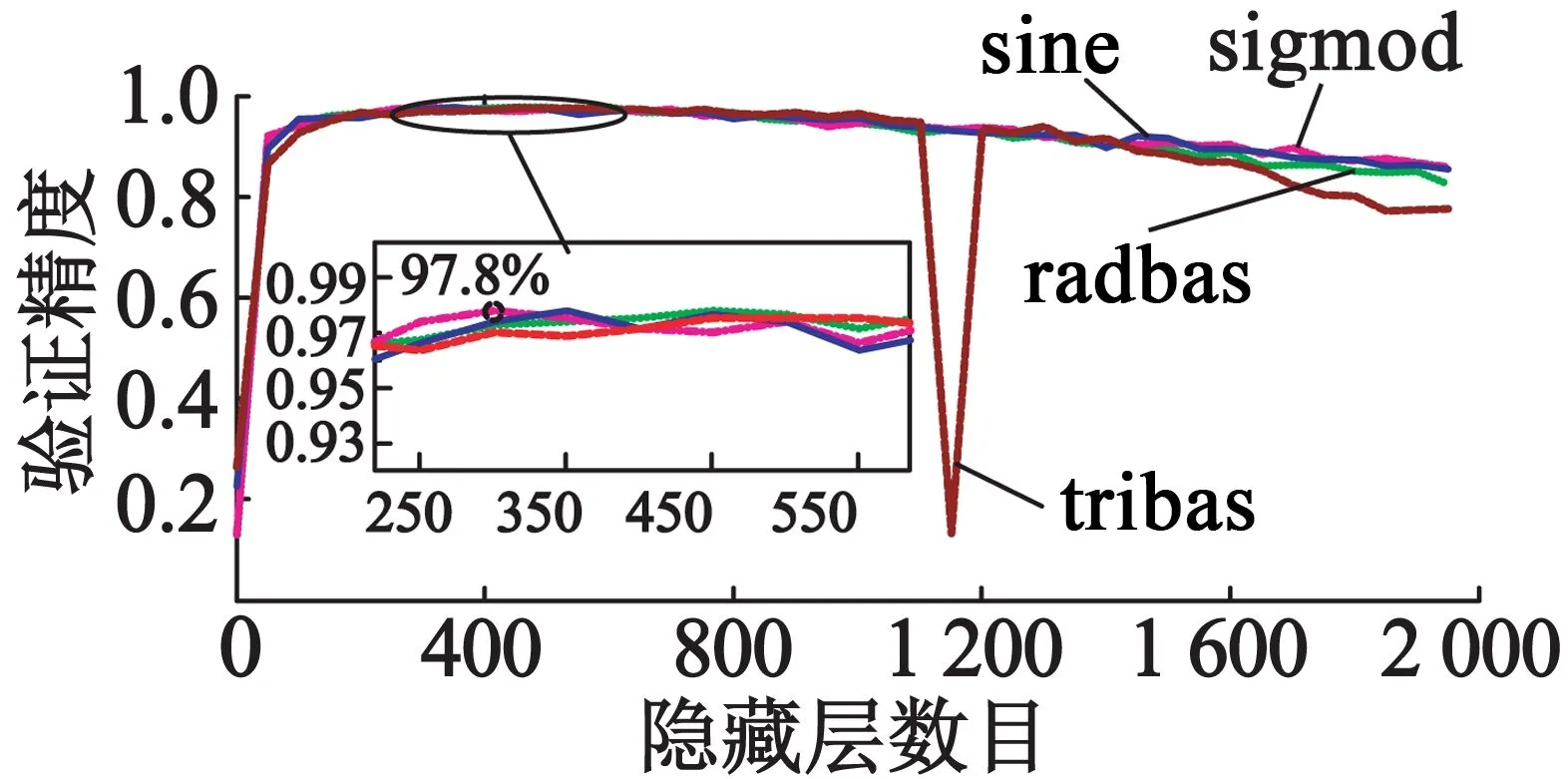
图8 ELM参数优化图

kNN算法与单个ELM算法参数已经确定，对于集成ELM而言，仍需要调试选择合适的阈值，以保证能够准确地分类并与kNN算法相互补偿。对于集成分类器2，阈值p用以确定单个ELM分类器的结果是否可信，若p，o值设置得过大，可能会导致高的分类精度，但同时会使得不可信的单个分类器变多，甚至所有的单个ELM分类器的结果都不可信；若p，o值设置得过小，将会导致分类精度降低，但是能够使更多的单个ELM分类器的分类结果可信。同样，阈值q的设置用于判断集成ELM分类器2的分类结果是否可靠，若q值设置得过大，将会使第二窗产生的不可靠样本增加，第三窗分类精度可能会有所降低；若q值设置得过小，在第二窗可能会产生更多的误诊断，导致分类精度降低。因此，合适的阈值是保证精度的重要因素，本文将p值设置为0，o设置为0.7，将q值设置为20。

3.3 仿真结果分析

为验证算法的有效性，通过MATLAB/Simulink仿真,诊断结果如表4所示。

表4 诊断结果

根据表4可知，测试样本集含有771组数据，在窗口1，kNN与集成ELM分类器1联合使用时，有760组数据被诊断，误诊断数为5组，该窗分类精度高达99.34%，11组数据诊断不可靠滑动到下一窗；在窗口2，仅有2组数据被诊断，该组数据诊断正确，该窗精度达到100%，前两个窗总共诊断数据762组，误诊断5组，精度达到99.34%，该窗有9组数据诊断不可靠，滑动到窗口3；窗口3采用kNN算法对故障数据进行全分类，共9组数据，误诊断3组数据，该窗精度达到66.67%，整个诊断过程误诊断数据8组，总精度高达98.96%。

表4中，Wi为i个窗，U(Wi)和C(Wi)分别表示第i个窗未分类样本数及已分类样本数，C(W)表示前i个窗已经分类数据总数，M(Wi)和M(W)分别表示第i个窗误诊断样本数及前i个窗误诊断样本总数，A(Wi)和A(W)分别表示第i个窗分类精度及前i个窗总分类精度。

4 在线仿真验证

为保证本文方法能够实时在线对SRD故障进行诊断，采用MATLAB/Simulink建立故障诊断模型，对SRD在额定、不同转速、不同负载转矩下对所提出的方法进行验证。在线仿真验证结构图如图9所示。

图9 在线仿真验证结构图

本文以功率变换器C相单个IGBT短路故障及转速传感器噪声故障为例,分别在以下三种工况下验证了本文算法的可行性：额定转速1 000 r/min、额定负载转矩110 N·m，额定转速1 000 r/min、过载120 N·m，低速600 r/min、额定负载转矩110 N·m。图10为额定情况下故障诊断结果，由图10可见，0.3 s故障发生，仅需要一个周期时间即7.5 ms即可对故障进行精确诊断。图11为额定转速、过载下故障诊断结果图，当故障发生后，仍可快速精确诊断故障。图12为额定负载、低速下故障诊断结果图，由于此时转速为600 r/min，一个周期所需时间为12.5 ms，因此仍能够在一个周期后精确诊断故障。

仿真验证了本文所提出的基于自适应滑窗的故障诊断方法能够在不同工况下仅通过一个周期内的电流特征信号对故障快速准确诊断。

(a) C相单管短路故障

(b) 转速传感器噪声故障

图10额定转速和额定转矩下故障诊断结果图

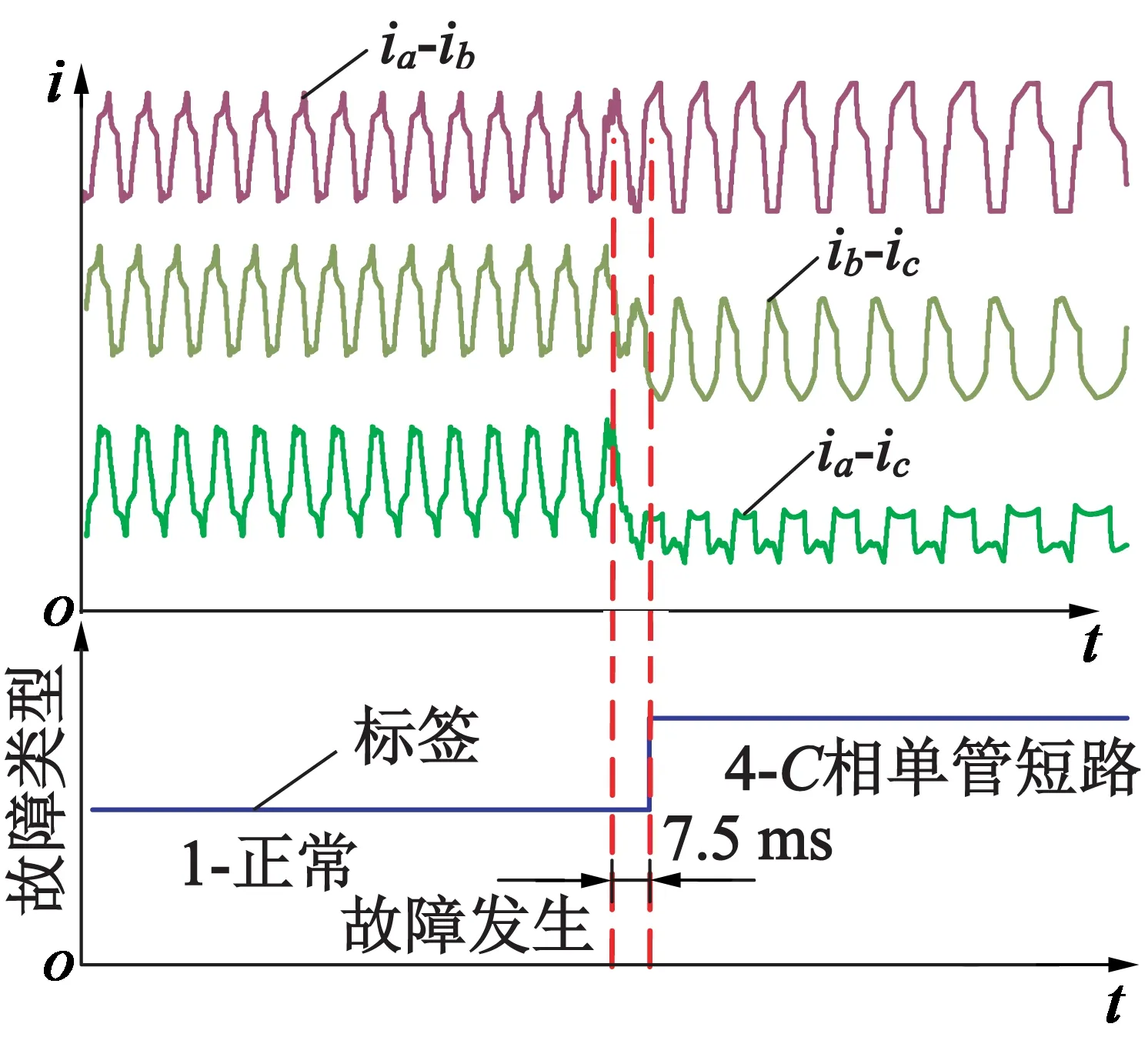
(a) C相单管短路故障

(b) 转速传感器噪声故障

图11额定转速和过载情况下故障诊断结果图

(a) C相单管短路故障

(b) 转速传感器噪声故障

图12额定负载和低转速情况下故障诊断结果图

5 结 语

本文研究了一种基于数据驱动的自适应滑窗的SRD故障诊断方法。开关磁阻电机相电流作为原始数据，FFT和ReliefF用作特征提取与选择，设计了kNN与集成ELM相结合的自适应滑窗诊断机制，以提高诊断系统的响应速度和诊断精度。离线与在线仿真实验验证了该方法在额定下仅需7.5 ms即可诊断功率变换器单个IGBT短路故障、相电流传感器和转速传感器噪声故障，诊断精度能够达到98.96%。此外，该方法不需要额外的传感器，且易于扩展，用于IGBT开路故障和传感器卡死、偏移故障。