扩散过程遍历性判别准则的注记

吴炳耀，梁明杰

（1.福建师范大学 数学与信息学院，福建 福州 350007；2.三明学院 信息工程学院，福建 三明 365004）

本文考虑半直线上[0，∞）以0 为反射边界的一维扩散过程，该过程对应的无穷小生成元为

其中a（x）＞0。 扩散过程遍历性的研究有很长的历史，相关结论已经丰富且完善，具体可以参考著作[1-2]和文献[3-10]。 著作[1]给出如下半直线上[0，∞）以0 为反射边界的一维扩散过程遍历性相关性质的判别准则，见表1。

表1 中“(*)+…”表示第一行中唯一性成立的判别条件再加上条件“…”，而最后一行的Nash 不等式仅限制于v＞2 的情形。一般，表中所列出来的性质从上到下逐行增强，但也有例外，对数Sobolev不等式和强遍历通常是不可比的，参见著作[2]第275～276 页例子5.8.1～5.8.2。

表1 一维扩散过程若干遍历性的判别准则

在实际的应用当中，通常情况下，已经知道扩散过程遍历，所以该如何给出遍历扩散过程满足更强遍历性质的充分条件是有意义且值得探讨的问题。 本文的目的就在于填补上述问题的空白，特别是给出遍历扩散过程何时满足指数遍历、离散谱存在、强遍历等性质的充分条件，进一步逐一举例说明这些充分条件的必要性。 最后，给出半直线[0，∞）上以0 为反射边界的一维扩散过程和上Ζ+生灭过程无穷小生成元形式上的对应关系。 关于生灭过程和扩散过程的一些重要性质可以参见著作[11-12]。

1 主要结果和证明

命题1 设半直线[0，∞）上以0 为反射边界的一维扩散过程遍历，则下面的结论成立：

（I）若

那么该过程指数遍历。

（II）若

则过程的离散谱存在。

（III）若

那么该扩散过程满足对数Sobolev 不等式。

（IV）若

那么过程满足Nash 不等式。

（V）若

那么过程强遍历。

证明：由于结论(I)～(IV)的证明方法类似，为了简便起见，只给出结论(I)的证明过程。 结论(V)的证明方法有别于结论(I)～(IV)，将单独给出结论(V)的详细证明。

即过程指数遍历。

（V）对任意 n≥1

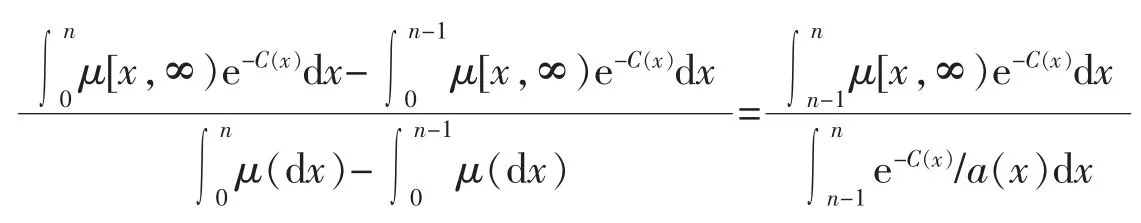
根据柯西定理可知，存在 ξ∈（n-1，n），使得

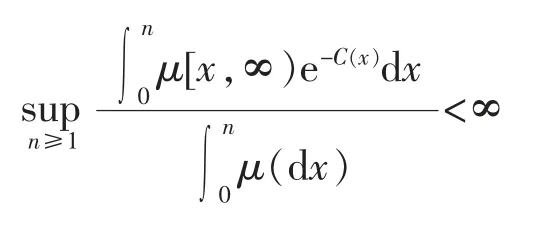
给出5 个例子来逐一说明命题1 中各个充分条件的必要性，这些例子受文献[1]，第154 页表8.3的启发。

例 1 设 a（x）=（1+x）γ，b（x）=0，其中 1＜γ＜0，则 C（x）=0

而

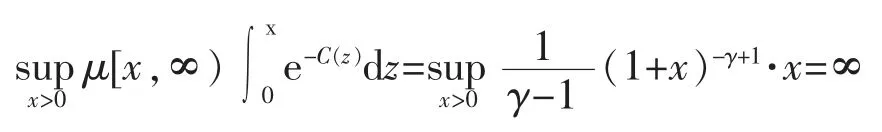
故过程不是指数遍历的。 注意到，此时

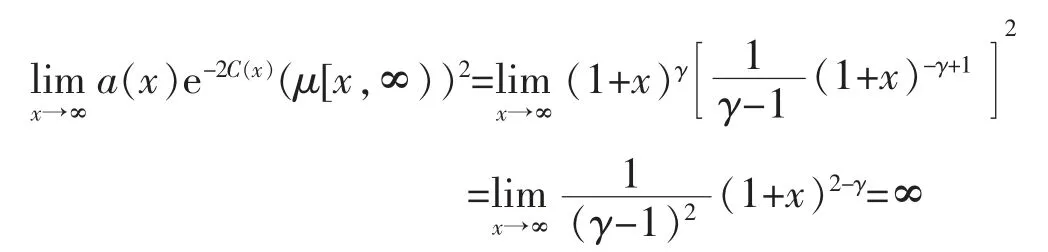
故条件(I)不满足。

例 2 设 a（x）=（1+x）2，b（x）=0，则

另一方面，由于

即过程离散谱不存在。

进一步

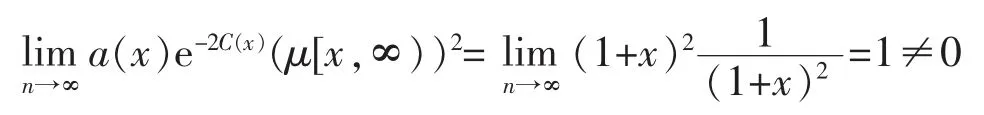
故条件(II)不成立。

例 3 设 a（x）=（1+x）2lg1/2（x+e），b（x）=0，那么，C（x）=0，且

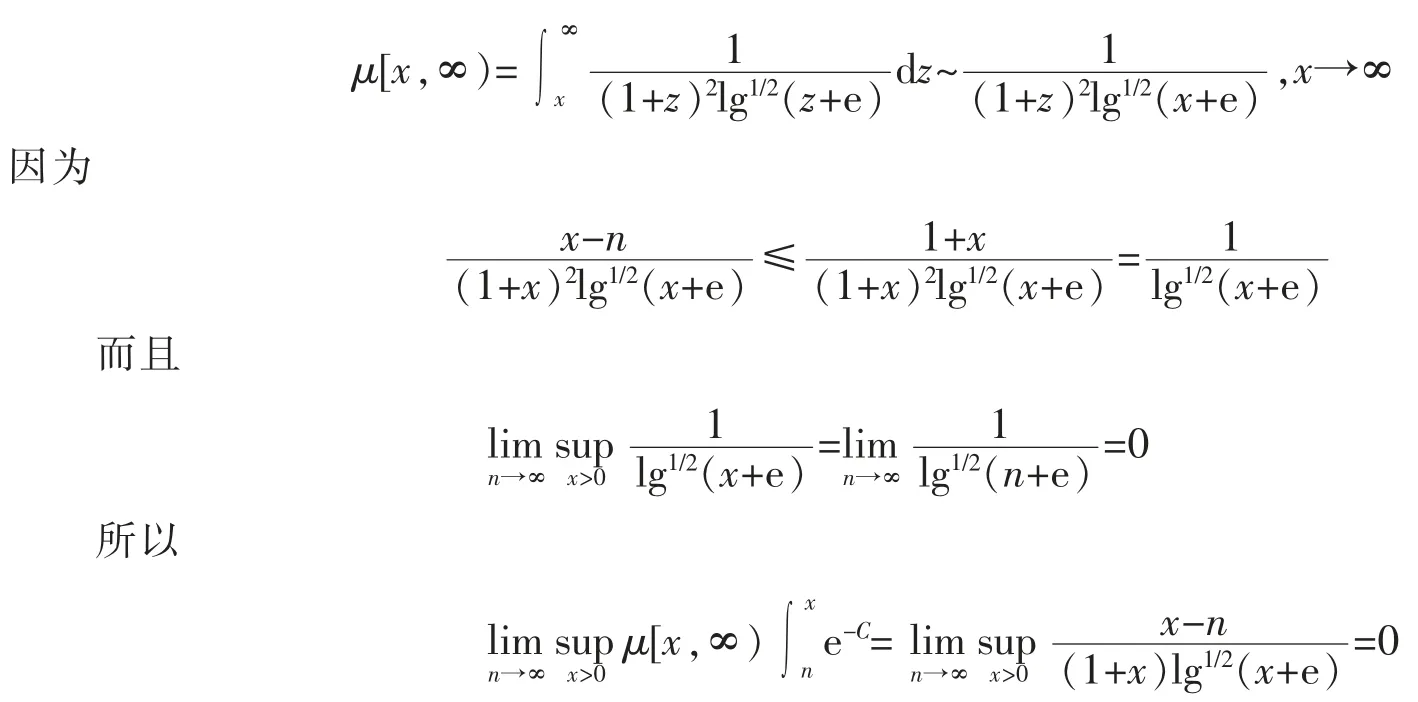
即过程的离散谱存在。

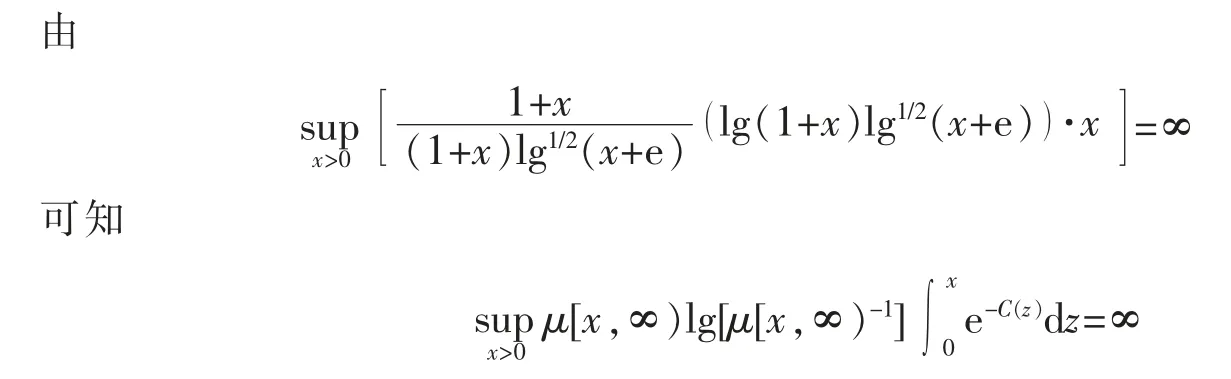
这样对数Sobolev 不等式不成立。

而

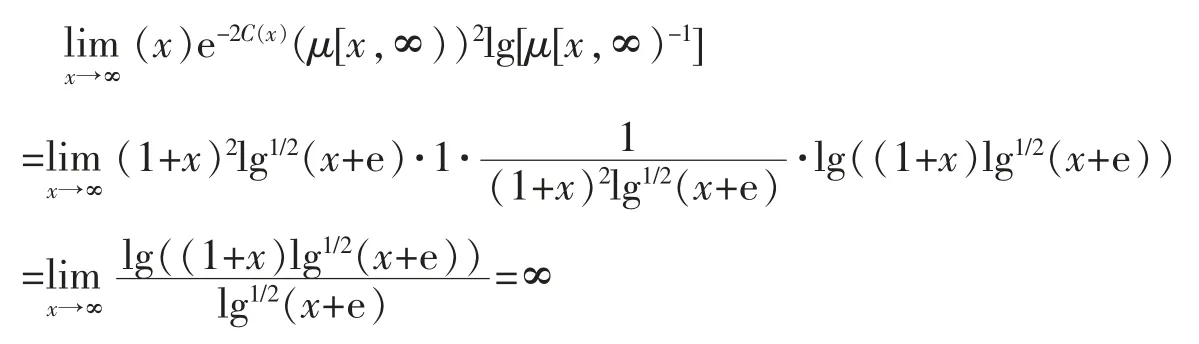
故(III)不成立。

例 4 设 a（x）=（1+x）2lgγ（x+e），b（x）=0，其中 γ＞1，那么，C（x）=0，

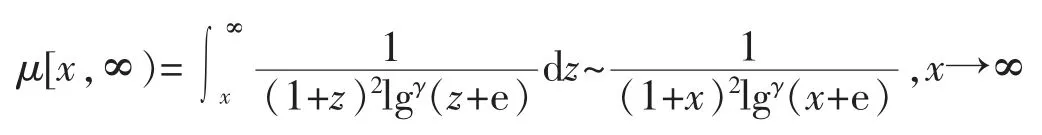
另一方面，根据

可知

因此Nash 不等式不成立。

此时

故(IV)不成立。

例 5 令 a（x）=（x+1）2lg（x+e），b（x）=0，则 C（x）=0，且

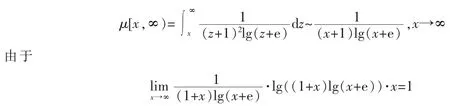
此时，

故条件(V)不成立。

下面给出半直线上以为反射边界的一维扩散过程和上生灭过程生成元形式对比的一个注记。

注1 一维扩散过程的无穷小生成元为

其中 a（x）＞0。 Z+上生灭过程的无穷小生成元为

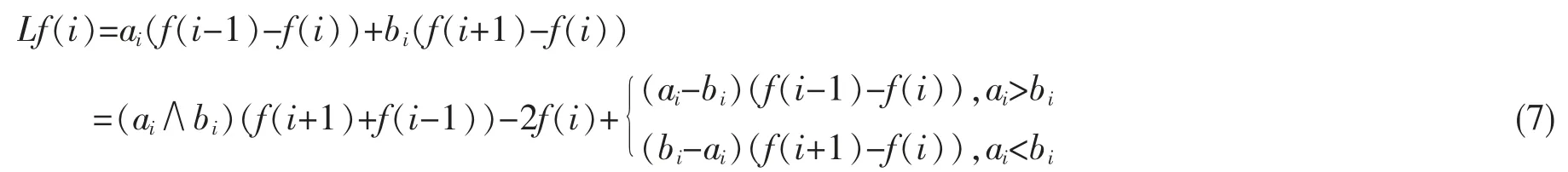
其中 ai＞0 和 bi＞0。

如果将Z+取值上函数的一阶变差理解为

而将函数f 的二阶变差理解为

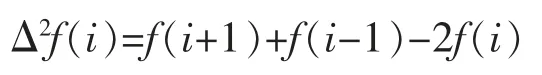
那么(7)可化为

对比(6)和(8)可知，a（x）与 ai∧bi相互对应，b（x）与 bi-ai相互对应。 特别的，当 ai-bi=0 即 ai=bi时，生灭过程对应于扩散过程b（x）=0 的情形。上述系数关系在著作[1]，第154 页表8.2，表8.3]中例子中得以充分体现。