基于“核心素养”的数学直观能力培养途径①

林新建

(福建省漳州第一中学 363000；闽南师范大学数学与统计学院 363000)

无论进行怎样的教学，培养学生的“数学直观”是非常重要的.本文从一道试题解法的探析入手，就其自然性的启示阐述“数学直观”在发展数学核心素养上的意义和途径.

1 “自然”的启示

例1(2010年高考全国卷理科21题)

设函数f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的单调区间；

(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围.

解析本题是2010年课标全国卷理科压轴题，试题的第(Ⅱ)问难住了众多师生，而高考标准答案同样也让他们费解——这样的解答是如何想到的呢？

这样的解答深奥难懂，解法极不自然，就是我们老师都看不懂，我们又该如何去跟学生讲应该这样解呢？

有没有较为自然简洁的解法呢？若有，怎么想到的呢？

注意到这是函数问题，我们不妨从“直观上”加以理解.

首先，“当x≥0时f(x)≥0”，直观意义即“f(x)在(0,+∞)上的图象位于x轴的上方”.

由于f(x)=ex-1-x-ax2，f(0)=0，f(x)的图象过原点，所以直观f(x)的图象在x=0右侧附近必须递增，从而f′(x)≥0对x=0右侧附近成立.

其次，因为f'(x)=ex-1-2ax，f′(0)=0，f′(x)的图象也过原点，所以直观f′(x)的图象在x=0右侧附近必须递增，从而f″(x)≥0对x=0右侧附近成立.

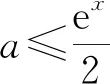
有了这个结果就好办了！接下来我们只要证明：

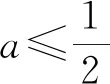
一道难题，由于对“直观意义”的挖掘，我们将解答进行得如此轻松！

2 直观的意义：抽象推理建模的思维基础

回顾以上探究历程，我们不难明白问题得以解决的关键所在——对题目意思所作的“直观理解”与最终结果的“直观预测”.

通常在理解题目阶段，需要对题目中的隐含条件和信息进行发掘，将抽象变具体，将隐含变清晰.而如何将“抽象变具体，将隐含变清晰”，这需要“数学直观”地“从事物的具体背景中抽象出一般规律和结构”，在这个过程中，“数学抽象素养”得到了培养和发展.

如何引领学生思考“按照怎样的线索、用什么方法去研究问题、解决问题”，

这需要“数学直观”地去“归纳、类比、联想、发现”.在这个过程中，“逻辑推理素养”得到了培养和发展.

如何引领学生思考“面对一个新的研究对象，从哪些角度发现和提出值得研究的问题？”这需要“数学直观”地去“发现模型、构建模型”.在这个过程中，“数学建模素养”得到了培养和发展.

例2(2012年高考新课标卷Ⅰ理科21题)

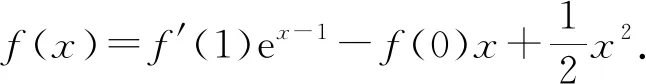
(Ⅰ)求f(x)的解析式及单调区间；

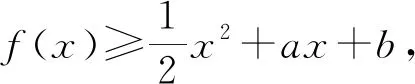
解析第(Ⅰ)问简单，难在第(Ⅱ)问.

现在的问题是，如何由ex≥(a+1)x+b，求(a+1)b的最大值呢？

这是难点，似乎无从下手，还得从“直观上”加以理解.

首先，直观函数y=ex与y=(a+1)x+b的图象，要使上式恒成立，必须a+1>0，从而知要使(a+1)b最大，必须b>0.

这是“从数量与数量关系、图形与图形关系中抽象出规律和结构”的“数学抽象”过程，所依赖的是“数学直观——直观理解”.

其次，直观要使得ex≥(a+1)x+b恒成立，函数y=ex与y=(a+1)x+b的图

象必须相切.

这是“从一些事实和命题出发，依据逻辑规则推出一个命题”的“逻辑推理”过程，所依赖的是“数学直观——直观判断”.

至此，只要设出切点(x0,y0)，利用相切条件得出a、b、x0之间的关系，进而得到(a+1)b关于a、b或x0的目标函数，问题不难获解.

这是“用数学知识与方法构建模型(函数模型)解决问题”的“数学建模”过程，所依赖的是“数学直观——直观预测”.

从以上的求解过程中，我们不难明白，正是缘于“直观理解”，我们对题目中的隐含条件和信息进行抽象，将抽象变具体，将隐含变清晰，同时借助“直观判断”对问题进行“逻辑推理”，借助“直观预测”进行“数学建模”.在这个“直观理解、直观判断、直观预测”的“数学直观”过程中，“数学抽象、逻辑推理、数学建模”等数学核心素养得到了培养和发展.

“数学直观”是我们学会用数学的眼光观察现实世界、学会用数学的思维思考现实世界、学会用数学的语言表达现实世界的前提，是我们进行数学抽象、逻辑推理和数学建模的思维基础.

3 直观的途径：直观引来“简洁美”

众所周知，“具体”中蕴含的信息具有丰富性、多样性，观察也可以有不同角度，因而从同一事例中可发现不同规律；同时，表面的东西大家都能看到，“藏在”背后的才有“含金量”.

所以，面对具体事例，关键是“你怎么看”？这是看问题的角度、高度以及切入点，需要知识的支撑，还需要历练.

学生经常出现“不是做不到，而是想不到”的尴尬，主要是他们的阅历还不足以使自己“想得到”.

教学中教师要在“你怎么看”上下功夫，即在如何“直观”上下功夫，引领学生直观问题的本质，感知问题特征，努力使他们“想得到”，将问题解答得简洁完美.

3.1 直观图形内隐特征

很多题目与图形密切相关，但图形的特征是内隐的，不容易被发现.若能将其特征予以直观，可以获得简单巧妙的解法.

例3(2013年高考新课标卷Ⅰ理科16题)

若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称，则f(x)的最大值是.

解析本题按常规方法求解较为繁琐，运算量也不小，若能直观函数的图形内隐特征，则可轻松将问题解决，且几乎没有计算量.

首先，直观函数f(x)有两个零点-1和1，又因为函数图像关于直线x=-2对称，所以感知f(x)还有两个零点-3和-5，从而得f(x)=-(x-1)(x+1)(x+3)(x+5).

其次，直观若将f(x)的图像向右平移两个单位，其最大值不会改变，于是问题转化为求函数g(x)=-(x-3)(x-1)(x+1)(x+3)的最大值.

易知g(x)=-(x2-9)(x2-1)=-(x2-5)2+16，其最大值为16，这多简洁！

评析由于“直观”，我们“从数量与数量关系、图形与图形关系中抽象出函数具有4个零点”，同时从条件出发，“依据逻辑推出若将f(x)的图像向右平移两个单位，其最大值不会改变”这一命题.在这个过程中，“数学抽象、逻辑推理”等核心素养得到了发展.

3.2 直观变量变化规律

变量的变化必然有其规律，只有直观变化规律，方能便于我们感知，进而依据变化规律将其轻松求解.

例4(2014高考课标全国卷Ⅰ第8题)

解析本题按常规方法求解较为繁琐，也需要耗费一定的时间，若能直观变量α、β的变化规律，问题瞬间可解.

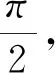
评析由于“直观”，我们“从数量与数量关系中抽象出α与β的关系及β的变化规律”，同时“依据逻辑进行推理”.在这个过程中，“数学抽象、逻辑推理”等核心素养得到了发展.

3.3 直观点线运动轨迹

点线运动有轨迹，只有直观轨迹特征，方能便于感知，进而依据轨迹特征将问题轻松求解.

例5(2009年高考新课标卷Ⅰ理科第10题)

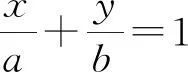
A．a2+b2≤1 B．a2+b2≥1

解析本题按常规方法求解似乎无从下手，若能直观动点M的运动轨迹，问题可轻松获解.

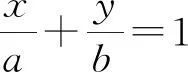
评析由于“直观”，我们“从数量与数量关系、图形与图形关系中抽象出动点运动的一般规律”，并“依据逻辑规则进行推理”，将问题的求解进行得轻松自在.在这个过程中，“数学抽象、逻辑推理”核心素养得到了发展.

3.4 直观模型结构特点

直观模型结构特点，进而借助模型求解问题，可将问题轻松予以解决.

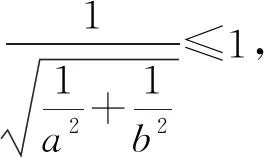
由于“直观”，我们“从数量与数量关系中抽象出一般的模型和结构”，并“用数学知识与方法构建模型解决了问题”.这是一个抽象、建模、推理的过程，在这个过程中，“数学抽象、数学建模、逻辑推理”等核心素养得到了发展.

例6(2011年高考大纲全国卷第12题)

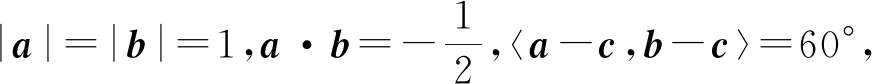
解析本题按常规方法求解异常繁琐，若能直观其模型结构特点，问题轻松可解.

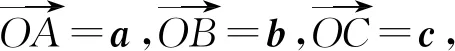
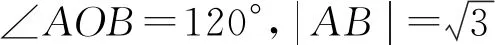
也是由于“直观”，我们“从数量与数量的关系中抽象出一般的模型和结构”，并“用数学知识与方法构建模型解决了问题”，在这个“抽象、建模、推理”的过程中，“数学抽象、数学建模、逻辑推理”等核心素养得到了发展.

3.5 直观思想立意要领

对于解题，绝大部分学生不是不会方法，而是由于没有站在思想的高度来思考和引领方法，或者是因为思想不明确而想不起来用什么方法来处理问题.因此，指导学生直观思想立意要领，运用思想引领方法就显得尤为重要了！

例7(2010年高考新课标卷Ⅰ理科11题)

若a,b,c互不相等，且f(a)=f(b)=f(c)，则abc的取值范围是( )

A．(1,10) B．(5，6)

C．(10,12) D．(20,24)

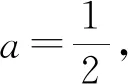
由于“直观”，我们“从数量与数量的关系中抽象出一般规律——问题的一般性”，再立意于“特殊与一般思想”对问题“从特殊到一般、一般到特殊”地推理，在这个过程中，“数学抽象、逻辑推理”等核心素养得到了发展.

例8(2011年高考新课标卷Ⅰ理科16题)

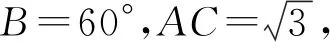
解析本题是三角形求解问题，解决问题的通法是“知三求三”，但是直观题目只给出一边一角，显然条件少了.

直观这是最值求解问题，需要引入变量，构造出待求最值关于这个变量的函数，为此不妨设∠A=θ，则∠C=120°-θ，由正弦定理得：

从而AB+2BC=2sin(120°-θ)+4sinθ

由于“直观”，我们“从数学的视角发现了问题(最值求解问题)，并提出问题、分析问题，构建模型(函数模型)”，再“依据逻辑规则进行推理”， 这是一个抽象、建模、推理的过程.在这个过程中，“数学抽象、数学建模、逻辑推理”等核心素养得到了发展.

4 结语：“直观”恒久，素养终成

经验之中有规律，是我们认识问题的一般过程和方法，也阐明了一个简单但很深刻的教学原理：经验是具体的，规律则是抽象的.规律不是从天而降的，而是从具体经验中经过不断归纳、概括才能得到的.

如何才能培养学生“从经验中发现规律”的能力呢？

首先，要培养学生从“从一般规律的高度考察具体事例”的意识，逐步养成“透过现象看本质”的习惯.这是观念问题，是思维习惯问题，也是思想方法问题，需要一个长期的、潜移默化的过程，需要有意识地培养.

其次，要让学生掌握观察事例、从经验中归纳规律、把具体事例中得到的东西概括到全体中去的基本方法，使他们逐步学会归纳、学会抽象、学会概括，进而形成“从经验中发现规律”的能力.

简言之，就是培养学生“直观”的习惯与“感知”的能力！

“直观”是一个人长期进行数学思维形成的，是逐渐养成的一种思维习惯，这个习惯日积月累就形成了数学素养.