中国初中算术教科书中分数概念

常红梅 代 钦

(1.内蒙古师范大学高等教育研究所 科学技术史研究院 010022；2.内蒙古师范大学科学技术史研究院 010022)

1 分数由来及其认识

在中国至迟到春秋战国时期已经有了分数概念.源于食盐分配、土地种植分配时不够分，量器或其他器具制造时单位换算等，也用在乐律研究、天文学研究中.刘徽曾言：“物之数量不可悉全，必以分言之.”(5)李迪．中国数学史简编[M].沈阳：辽宁人民出版社，1984：90.他对分数的概念做了精辟的概括.《九章算术》中已经有了比较完整的分数计算方法，后来何承天(公元370—447年，东海郯人，生活于东晋与南北朝期间，在南朝刘宋初为太子率更令，为当时著名的天文学家)创造了一种分数近似算法，应用于古代的历法计算中.(6)李迪．中国数学史简编[M].沈阳：辽宁人民出版社，1984：111.

分数，自古以来在数学教育中扮演着重要角色，因此，在中小学数学教科书中如何安排分数内容是一项极为重要的课题.分数，一是源于生活，反映了整体与部分之间的关系，它表示一个量的多少；二是源于数学内部发展需要，由于除法运算的结果有可能跃出整数的范围，所以需要引进新的数——分数，进行扩充.(7)章敏.关于分数教学的思考[J]．课程·教材·教法，2015(3)：64.

“分”数，顾名思义是分出来的数，“把一个整体平均分成几份，取其中的一份或几份”，这个定义表示部分与整体的关系，强调分数是一个量.但是分数产生于测量过程(整体或一个单位的一部分)和计算过程(除不尽时得到分数)(8)范文贵.分数的内涵有多大？——兼谈小学分数的教学[J]．人民教育，2011(7)：43..因而分数还有一种定义是：“实如法而一，不满法者，以法命之.”(9)注：法数、实数为中国古代数学中的称呼，法数为除数，实数为被除数.就是说，如果被除数或余数小于除数，就得到一个以除数作分母的分数，强调分数是一个数.那么，“分母”、“分子”的叫法又是从何而来的呢？依据传统算术中“法”和“实”的命名来源，得到我国古代度量具有“法”的意义.其所谓“实如法而一”，即是“以法量实”，“实”中有等于“法”的量，所得是一，“实”中有几个“法”，所得就是“几”.(10)李继闵.算法的源流——东方古典数学的特征[M].北京：科学出版社，2007：44.而分数在分割测量中产生，“法”即相当于“母”，“实”相当于“子”，“子”由“母”所孕育，“母”在下、“子”在上，“母”背着“子”，因而“分母、分子”形象地描述了分数上下两个部分的关系，一直沿用至今.

张奠宙先生认为，按人们认识发展的顺序，分数定义一般有如下四种情况.(11)张奠宙.分数定义[J]．小学教学(数学版),2010(1)．

定义1(份数定义)：分数是把一个单位平均分成若干份之后其中的一份或几份.

定义2(商定义)：分数是两个整数相除(除数不为0)的商.

定义3(比定义)：分数是整数p与整数q(q≠0)之比.

在新农村经济建设的过程中，循环性经济主导型能够推动新农村建设，实现农业的良性可持续发展，是农业发展的重要途径，为了实现循环主导型的农业生态建设，需要人们以可持续发展观为基础理念，满足我国农业发展的实际情况，为指导我国农业发展打下基础，在保护我国生态农业的基础之上，再调整我国农业发展内部的产业结构，提高农业生态的效益，提高生态园的经济，实现农业生态园的健康可持续发展。

定义4(公理化定义)：有序的整数对(p，q)，其中q≠0.

“份数定义”是直观的认识，讲整体与部分的一种关系；“商定义”、“比定义”则是由直观到抽象，认为分数是一个数，是除法运算的结果；而公理化定义在初中分数中是用不到的.

现在人们认为分数是小学数学的教学内容，其实并不是这样.从历史的角度看，在1902到1961年间，较复杂的分数及其应用在初中数学教科书中被设置.这里需要说明，自清末“钦定学堂章程”至1922年“六三三”学制颁布之前，小学分为初等小学和高等小学两个阶段.其中高等小学相当于初中.故高等小学和“六三三”学制之后的初中统称为“初中”.1961年以后，在初中不设置算术(12)课程教材研究所.20世纪中国中小学课程标准·教学大纲汇编(数学卷)[M].北京：人民教育出版社，2001：426..清末民国时期至1949年中华人民共和国成立以后到1961年期间，中国初中数学教科书中分数概念表述和内容编排等经历了复杂的过程，对这一历史发展过程进行研究具有重要的理论价值和现实意义.

2 清末初中算术教科书中分数的概念表述之演变

1902年颁布《钦定学堂章程》之时,中国数学教育正处于百废待兴之际,虽然有了制度,但是一时还没有根据数学教育制度编写中学数学教科书的客观条件,国人只好选择一些外国数学教科书进行翻译,并没有充分考量这些教科书是否符合中国数学教育制度的要求和国情，处于饥不择食的状态.从整体上看,在清末翻译的初中算术教科书并不一定和数学教育制度要求相一致,具有一定的独立性.

2.1 编译算术教科书中之分数

编译的初中算术教科书中分数的概念表述有份数定义、商定义和比定义，为说明问题简单起见，本文甄选清末编译的6种较典型的初中算术教科书为例，阐述分数概念表述与其表达的意义.因为教科书中分数概念的表述学习中常常将其表达的意义放入其中讲解，所以下文列在一起分析，如表1.

表1 清末编译国外初中算术教科书中分数概念表述及意义之分析

由表1可见，清末初中算术教科书中分数概念是以份数定义为主，引导学生学习不够整数时，表示量的大小可以用“分数”，而分数是将整体分为若干部分，而部分占整体的份数.而“商定义”更倾向于除法计算，是商不足整数时用分数来表示.“比定义”是在份数定义的基础上，凸显一个比率关系，与商定义又是相通的.在日本的东野十治郎著，日本西师意用中文翻译的《最新算术教科书》中阐释分数的定义时用线段图表示了两种意义，一种是单位的三分之二，一种是二倍之三分之一，如图1.

图1

2.2 国人自编算术教科书中之分数

清末国人自编的初中算术教科书中分数概念的表述主要是份数定义.本文选取2种较典型的初中算术教科书为例，呈现分数概念表述与其表达的意义，如表2.

由表2可知，《最新算术教科书》中分数的定义指出将整数“一”均分取其一分或数分，体现整体与部分的关系.而《高等小学用最新笔算教科书》中分数的定义以举例说明概念，从几分之一到几分之几有一个推理过程.提到了分数单位，体现整体与部分关系，倍比关系.以上两种分数的定义很简单，直接给出一个整体与部分的关系，并描述其形式，旨在让学生理解整数与分数的区别.

表2 清末国人自编初中算术教科书中分数概念表述及意义分析

3 民国时期初中算术教科书中分数概念表述之演变

3.1 编译国外算术教科书中之分数

在民国时初中算术教科书基本都是国人自编，编译教科书极少.目前所掌握的仅有一种，即[日]藤泽利喜太郎著，赵秉良译的《中学算术新教科书》(1915年，商务印书馆).其中的分数定义是：凡除法除至实数小于法数时，则将剩余记于上，法数记于下，而于其中划一横线以表示其商者，作为分数形，称之曰分数.书中直接以除法定义分数，指出被除数小于除数时，将商以分数形记之，体现分数作为一个数在计算中的意义.

3.2 国人自编初中算术教科书中之分数

民国时期，国人自编初中算术教科书共20种，算术教科书仍处于多元化发展阶段.分数的定义描述演变如下：

①1913年～1917年，骆师曾，寿孝天著《高等小学校共和国教科书新算术(笔算)第三册》的分数定义与北京教育图书社编《高等小学实用算术教科书(第三册)》中分数的定义完全相同，即表示1单位平分为若干份，而取其一份或几份之数，体现了整体与部分的关系；而徐念慈编的《正订近世算术》中分数的定义也大致相同，只是除了“分”还强调了“聚”，这里的“聚”是指以几个分数单位来合成集聚一个分数，体现整体与部分及倍比关系，也包含着一种整体与部分转化的思想.

②1919年，寿孝天编的《中学校用共和国教科书算术》(廿四版，1912年初版，一直沿用到新学制的颁布)中分数的定义则有所不同，描述为：除法遇有残数时，曾记以分数Fraction.分数者，写数字于横线之上下，读为若干分之几者也.其若干即除数，写于线之下，曰分母Denominator.其几即被除数，写于线之上，曰分子Denominator.分母除1所得之数，为分数之单位Fraction Unit.分母除分子所得之数，为分数之值Value of fraction.这是典型的“商定义”，以除法定义分数，分数单位也以除法定义，且名词术语都加了英文翻译.这里在相关概念后边附加英文名词术语，说明受到国外影响.同时也给出分数的直观说明.而同年出版的陈文著《实用主义中学新算术》中分数的定义却与之相异，承前之“份数定义”，并体现了倍比关系.

③1927年，严济慈编的《现代初中教科书算术(上册)》中，首先以“聚拢多少个一，所成的数叫整数”引出分数的定义：把这个一随便分成几等分，聚拢多少个这种同样的等分，所成的数叫分数(Fraction)，而后举例说明：譬如说三个五分之一称为五分之三；就是把一分作五等分，取三个这样的等分聚拢起来(如图2).定义中提到“等分”、“聚拢”，体现整体与部分、倍比关系.1930年，薛溱舲，龚昂云，杨哲明著的《初中算术(下册)》中分数的定义与上述定义大同小异，平分的单位由“一”变为“1”，“聚拢”写做“集”.

④1932年，吴在渊，胡敦复编的《初级中学用中学算术》中分数的定义突出将“1”进行等分，提到名分数，即：若所分的1是1尺，1两，等名数，便叫名分数.并以分线段举例(如图3)，有a，b二线分，要拿m做长的单位去量.因a，b都比m短，不够量，就把m分做5等分，取出1份做小单位，拿它来量a得1倍，量b得3倍.a是m的五分之一，b是m的五分之三.突出分数的测量意义，强调“比定义”，体现整体与部分、倍比关系.书中也提到“分数也可表明分母除分子的数值.”讲了分数与除法的关系.而1933年，刘秉哲著的《初级中学算术》中分数的定义表述，又强调把“一”随意等分，体现整体与部分、倍比关系，在分数的解释中用除法解释分数，指出分数的值相当于商，强调数概念.

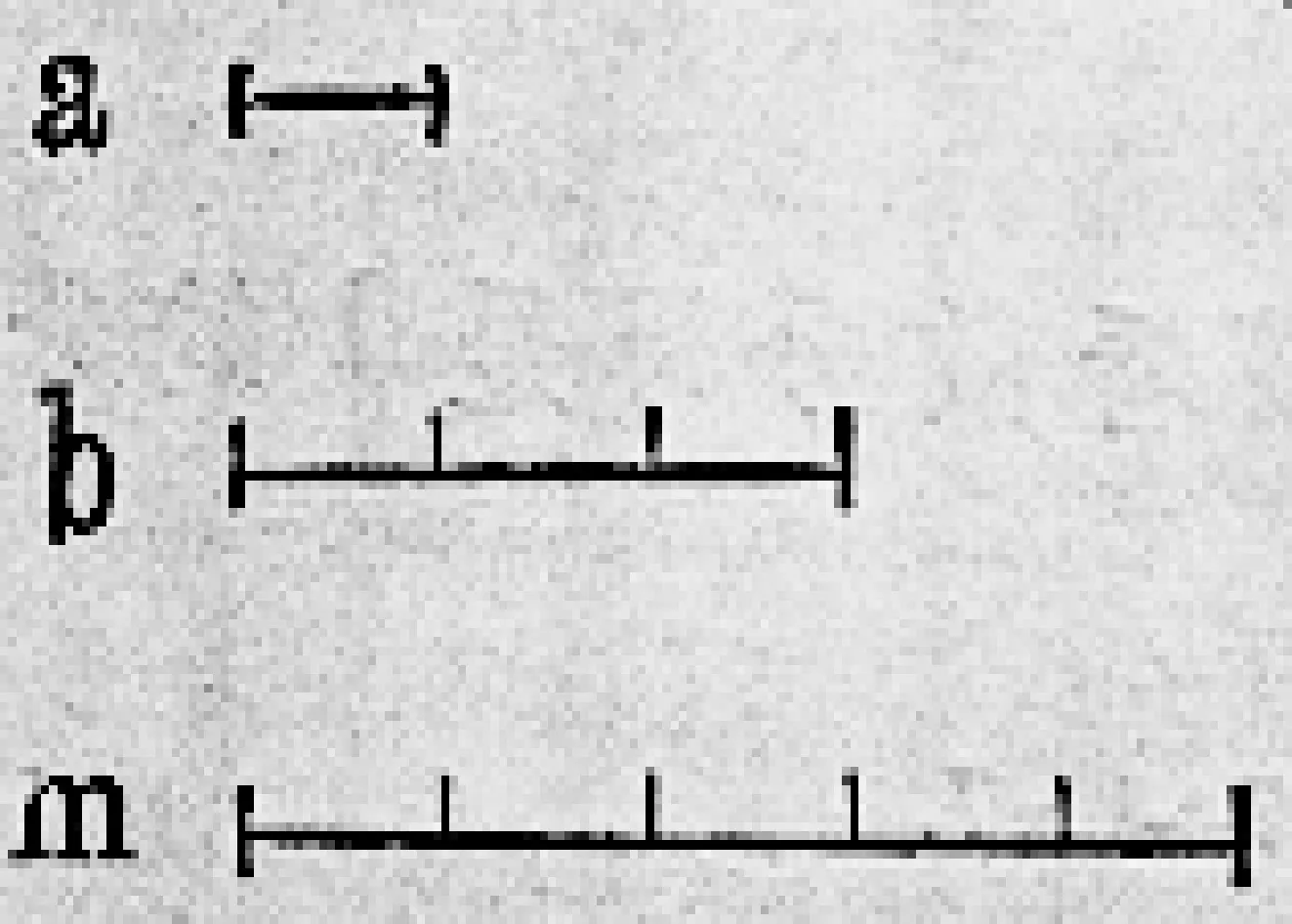
图3

可见，这个时期，除了讲份数定义，还强调分数的除法意义，且国人自编的算术教科书大多是参照日本算术教科书编写的.

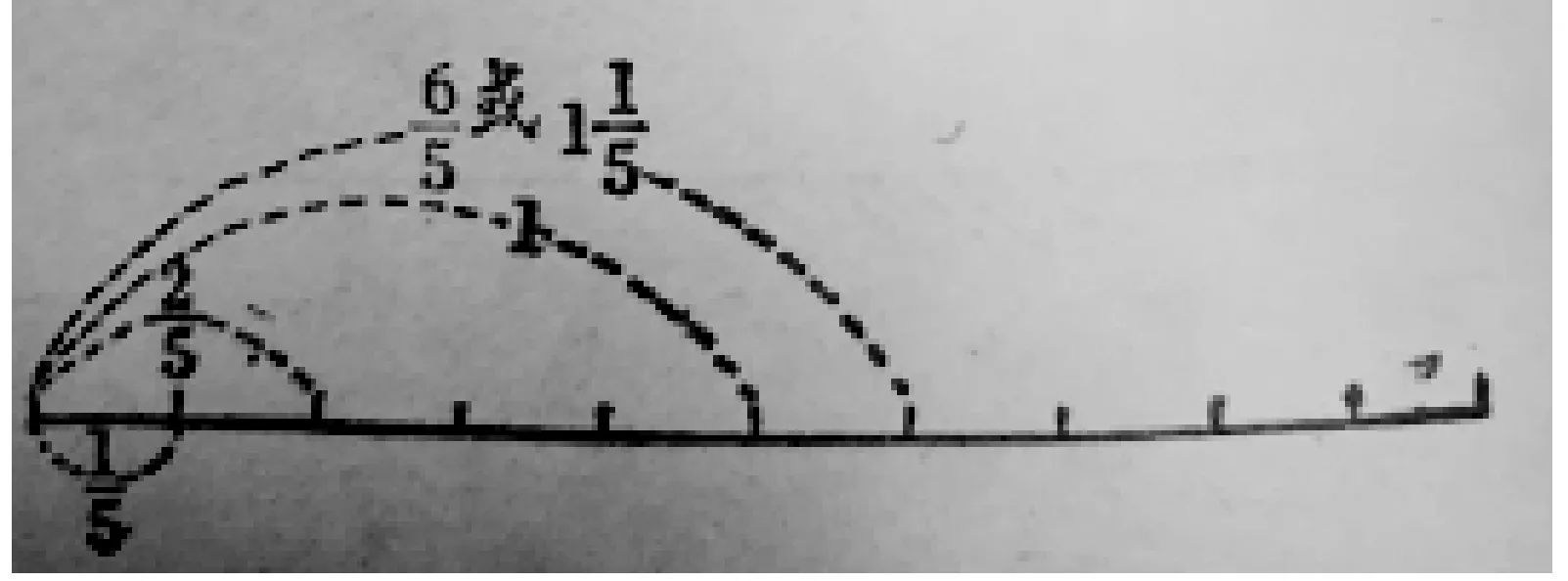
图4

图5

图6

此外，1934～1937年，王刚森著的《王氏初中算术(下册)》、陆子芬，孙振惠，石濂水编的《新课程标准适用初中算术(上册)》中分数的定义与骆师曾，寿孝天著的《高等小学校共和国教科书新算术(笔算)第三册》中分数的定义相同.周为群，刘薰宇，章克标，仲光然合编的《开明算学教本算术(下册)》、蔡泽安编的《初中新算术(上册)》中分数的定义也与之大同小异，只是这两本教科书分别强调要分的是“一种单位或一个全数”、“一个数或一个量”，突出了分数既可以作为数，也可以作为量的意义.

⑥1941～1945年，张幼虹著的《修正新课程标准适用实验初中算术》中分数的定义指出，把“一整数或整数1”随便等分；而王桂荣，余信符著的《建国初中算术(上册)》中只简单地描述为把“一”等分.这一时期分数定义均体现了整体与部分的关系，强调分数作为数的意义.

⑦1947年，魏怀谦编的《新编初中算术(上册)》中强调分数的两种定义，一种是商定义，一种是份数定义.商定义中指出：将整数1，分作若干等份，取出若干等份；所取之数对全数说，叫做分数.以分母除分子之商，叫分数值，也叫分数.份数定义中描述为：将一整数，分作若干等份，取出若干份；所取之数，叫作分子，全份数叫作分母，以分母除分子之商，叫做分数值.从中可见，其实两个定义是一样的，只是前者将整数1等分，而后者是将一整数等分，不过前者更强调数，后者突出量.1948年，国立编译馆，蔡德注编的《初级中学算术(上册)》中分数的定义只简单指出把“整数1”等分，突出以数的形式定义分数.

由上述可知,在清末民国时期初中算术教科书中分数概念的阐释，大多用“份数定义”，而且以除法解释了分数的意义，少部分用“商定义”或“比定义”.1919年以后分数概念的名词术语都标注了英文，便于学者结合中外文进行更深的认识.而且教科书中多用线段图来导入或解释分数的概念.综上，初中分数概念表述相比较清末而言更注重引导性，易于学生接受，并且更加全面、规范化，使学生在学习分数概念知识的同时了解其思想方法.以下将典型教科书中分数定义方式及演变过程总结，如表3.

表3 国人自编典型初中算术教科书中分数的概念表述及意义分析

从以上典型教科书中分数的定义可知：国人自编的初中算术教科书中，分数的概念表述也是集中在份数定义与商定义.其中份数定义居多，但是表述中也有细微的差别，隐含着教科书编著者对分数概念的理解.如：《最新算术教科书》、《现代初中教科书 算术》、《复兴初级中学教科书算术》中均以等分“一”来定义分数，而《初级中学用新中学算术》则指出将“1”等分，这个区别看似微乎其微，却体现了数学发展的抽象概括性，从整体中抽象出单位“1”.《开明算学教本算术》中的“一种单位”或“一个全数”即是从“一”向“1”的过渡.另外，《初级中学用新中学算术》、《初级中学算术》、《骆氏初中算术》虽然是从整体部分的角度定义分数，但都在解释分数的意义中阐述了分数与除法的关系.可见，分数概念表述的两种方法也不是截然区分的.然而，《中学校用共和国教科书算术》是直接以整数相除定义的，明确了分数与除法的关系.此外，在概念的引入方式上也有不同，其中《现代初中教科书算术》以整数的含义引出分数的含义，有利于学生对比整数与分数的区别，更好地理解分数；《骆氏初中算术》用均分线段来引出分数的定义，形象性更强，使学生更容易理解分数的含义；几本书中图形的例证，更容易引起学生的学习兴趣，从而激发知识汲取的积极性.此外，通过分数含义的解析来理解分数的意义，其中分数含义中体现的整体与部分、测量、倍比、除法、集合等关系是分数意义学习的重点知识.

在当时的《数学辞典》和《算学辞典》中对“分数”的定义具体如下：

(1)《算学辞典》(段育华、周元瑞编，商务印书馆，1938年)中的定义.

分数平常分为两种，即普通分数(Vulgar fraction)简称分数(或称命分)及十进分数(Decimal fraction)(常称小数)是也.普通分数者，表示分母可为任意量之分数也.十进分数即小数，不书分母而分母常为10之乘方之分数也.

此定义中突出分数单位，介绍了普通分数与十进分数(小数).

(2)《数学辞典》(倪德基、酈禄琦、雷琛编，中华书局，1925年)中的定义.

这个定义中突出分数的除法含义，体现了分数与除法的关系.

4 结语

分数是数学中内涵丰富的核心概念之一，是人类重要的文化成果.在清末民国期间,初中算术教科书逐渐从主要翻译、编译美国、日本的教科书发展到自编教科书，且书中内容体系逐渐完善，这体现了中国对西方数学教育的学习与吸纳，最终发展为本国数学教育内容的一个演变过程.分数的定义方式主要突出了整体与部分的关系，也显示了分数与除法及比的不可分割性.正如算术是解决实际问题的学科，注重计算方法，分数也是来源于现实生活，为解决除自然数以外的“分出来”与“除出来”、“比出来”的数的问题.另外，一些初中算术教科书在引入分数概念时，常常提到对非整数的表示方法除小数之外，另有一种表示方法即分数.但没有深入地介绍小数实质上也是一种分数，即十进分数，以10的倍数为分母的分数.

比较而言，份数定义更强调分数作为量的意义，用于测量；商定义更强调分数作为数的意义，用于分数的四则运算.份数定义是基本的分数定义，对于初学分数者，更容易接受.因而依据分数的来源，引导学生先学习份数定义，再学习商定义、比定义，既符合从直观引入到抽象概括的教学方法，又遵循了从分数作为量的体验到分数作为数的理解的学习心理规律，达到事半功倍的教学效果.因此对分数概念的不同界定及其相互关系的系统认识，对教学研究和实践均有重要价值.