为表达世界而建模——《指数函数》三次备课思考

张玲玲

(常熟市梅李高级中学 215500)

《普通高中数学课程标准(2017年版)》(以下简称《课标》)指出：“数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识和方法构建模型解决问题的素养.”数学建模具有重要价值，它“是应用数学解决实际问题的基本手段，也是推动数学发展的动力.”虽然在过去的教学中，一些教师也关注到数学建模，但多数教师仅仅限于专题讲座或者对于特殊的教学内容在教学过程中加以体现，并没有把数学建模作为高中数学核心素养贯穿在日常的教学过程中.那么，如何结合具体内容的教学，以具体知识为载体，让学生经历数学建模过程，学习数学建模的方法，提升数学建模素养，进而养成用数学语言表达世界的思维习惯，这是值得深入研究的问题，也是教学观念的重大转变.本文结合“指数函数”的三次教学设计过程，对此作以探索.

1 关注载体，为获得知识而建模

指数函数是学生在学习了函数的概念、图象与性质后，学习的一个新的函数模型，也是运用研究函数的方法研究函数的一次实践．通过指数函数的学习，学生可以进一步深化对函数概念的理解，为研究对数函数、三角函数等其他初等函数打下基础.因此，指数函数的概念、图象、性质、运用等基础知识非常重要，这些知识既是进一步学习函数的基础，也是学生经历一次建立数学模型过程的有效载体.在第一次教学设计时，我们首先要梳理清楚指数函数的知识体系.

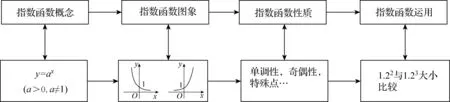
在教学过程中，为了帮助学生建立起比较完善的知识结构，本节课就要解决如下问题：

问题1什么是指数函数？

问题2怎样画出指数函数的图象？

问题3指数函数有哪些性质？

问题4如何比较下列各组数的大小？(1)1.52.5,1.53.2;(2)0.51.2,0.5-1.5.

问题5本节课你学到了哪些指数函数的知识？

这些问题的解决，可以使学生获得指数函数的基础知识与基本技能，形成指数函数的知识结构，为学生后继学习与思考奠定基础.当然，知识、技能不是课堂教学的最终目标，而应是一种有效载体，让学生在知识、技能获得过程中，获得建立指数模型的方法，感悟用数学语言表达世界的观念，以实现数学教育的更大价值.目前一些教学设计，特别是一些“活动单”“导学案”“学案”的设计，都仅仅停留在知识、技能的获得层面，无论课堂教学过程中是否采取“探究”“合作”“交流”活动，实际上学生得到的只是“是什么”，快速到达“目的地”.这样的教学，貌似提高了学生的学习效率，其实对提升学生数学素养是不利的.

2 关注过程，为获得方法而建模

《课标》指出，数学建模的过程主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、改进模型、解决问题等.数学建模不仅仅是最后的数学模型，更为主要的是借助于日常的数学活动，以具体的教学内容为载体，让学生经历数学建模过程，学会数学建模的基本方法.指数函数是高中数学的一个典型的数学模型，借助于指数函数模型的建立过程，引导学生感悟数学建模的基本方法，是指数函数的重要教学目标之一.在第二次教学设计时，我们认真梳理指数函数的生成过程与学生的思维过程.

问题1某种放射性物质不断变化为其他物质，每经过一年，这种物质剩余的质量是原来的84%．如果经过x年，该物质剩余的质量为y，x与y之间具有怎样的关系？

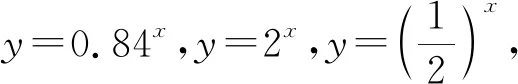
你有什么发现？

问题3结合以前研究函数的方法，我们怎样研究指数函数?

问题4指数函数的性质可以解决哪些问题？

这些问题的解决，让学生从实际情境中发现问题、提出问题，先建立特殊的指数函数模型，进而得到一般的指数函数模型，并对其中的参数进行讨论，画出图象，探究指数函数的性质，进而用这些性质去解决一些简单的问题.在建立与研究指数函数模型的过程中，学生体会并获得建立数学模型的基本方法.同时，也获得相应的数学知识.这里的过程，既是数学建模的过程，也是学生思维的过程，只有让学生经历这样的过程，才能获得一般的研究方法，进而形成思考一类问题的思维习惯，学生不仅获得“是什么”，同时获得“怎么做”.

3 关注理念，为表达世界而建模

为了实现指数函数的教育价值，使指数函数成为学生研究函数一般方法与过程的典型案例、成为学生经历数学建模过程的有效载体，让学生在指数函数的学习过程中体验用数学语言表达世界、感悟数学与自然的紧密联系.在第三次教学设计时，我们重新思考，坚持培养学生数学建模素养的理念，对本节课的明线(知识)、暗线(过程与方法)进行重新梳理，有机融合.

在教学过程中，要帮助学生养成“为表达世界而建模”的思维习惯，让学生在获得指数函数的知识过程中，体会数学建模的方法，本节课最终教学设计如下：

(1)创设情境，提出问题

情境2某种放射性物质不断变化为其他物质，每经过一年，这种物质剩余的质量是原来的84%．如果经过x年，该物质剩余的质量为y，x与y之间具有怎样的关系？

情境3《庄子·天下篇》中有一句话，“一尺之棰，日取其半，万世不竭”．如果经过x天，该木棰剩余的长度为y，x与y之间具有怎样的关系？

问题1你能写出这几个问题的函数模型吗？

设计意图引导学生建立具体的指数函数模型，感受指数函数与自然世界的联系．让学生感受到这些模型与初中已经掌握的一次函数，二次函数，反比例函数是不一样的，进而发现问题，提出问题.

(2)建立模型，获得概念

问题2通过这几个函数，你发现了什么？

设计意图引导学生从具体实例中概括典型特征，从“特殊”到“一般”进行抽象，建立指数函数模型，并尝试自己给出指数函数的定义. 让学生在建立指数函数模型过程中，学会用数学的眼光观察世界，再用数学的语言表达，进而培养学生数学建模素养.

数据挖掘系统构架按不同层次划分为4部分：云计算平台、数据准备、数据挖掘算法和数据分析(图3).云计算作为整个系统架构的底层计算平台，借助云计算的处理能力，完成数据的清洗、集成、选择和加载等准备过程.为了支持数据挖掘算法中的分析型查询操作，同时还需为数据建立索引.借助于这些方法便可实现面向大数据的各种应用，如时空模式发现、可视化分析等.

(3)研究模型，感悟方法

问题3怎样研究指数函数呢？

设计意图引导学生回顾初中研究一次函数，二次函数以及反比例函数的研究内容和方法，从两个角度思考：

(i)从指数模型的解析式出发，从“数”的角度去研究这个模型.

对于一般的数学模型，怎样选择“突破口”？在探究学习的过程中，学生可以通过选择一些“特殊”的数进行探究，也可以对“式”进行逻辑分析，推理出一些结论. 例如：对于y=2x，可以对自变量x赋值，观察与之对应的y是如何变化的；也可以令其中的x为-x，观察对应得到的y的变化情况.

(ii)从指数函数的图象出发，从“形”的角度去研究这个模型.

如何画出指数函数的图象？先回顾初中时掌握的“描点法”的作图步骤：列表，描点，连线；然后结合这些步骤，给学生布置任务：选取数据，画出图象，观察特点，归纳性质.

问题4指数函数具有哪些性质？

设计意图在探究性质这个环节，让学生小组合作，无论是从“数”的角度、还是从“形”的角度出发，都要注意“代表性”、“逻辑性”. 例如，在同一个坐标系中多作几个函数图象，进而“读”出指数函数的性质，再尝试进行简单的证明或者说明.

通过探究活动，使学生对指数函数的研究过程与方法有了深刻的认识．学生可以从“数”的角度去“读”，是对符号语言的理解，学生也可以从“形”的角度去“读”，观察图象，是对图形语言的理解，为以后研究函数模型乃至数学模型奠定方法基础．

引导学生经历从“特殊”→“一般”→“特殊”的认知过程，从合作交流、共同探讨中的氛围中，认识指数函数的概念、图象和性质，同时了解指数函数的实际背景和研究函数的基本方法；体会分类讨论思想、数形结合思想，增强学生识图用图的的能力.

(4)运用模型，解决问题

问题5怎样比较下列各组数中两个值的大小？

(1)1.52.5,1.53.2;(2)0.51.2,0.5-1.5;(3)1.50.3,0.81.2.

设计意图通过指数函数性质的简单应用，体会构造函数的思想(同底和不同底的两种类型)，再运用指数函数的单调性解决问题，也包含了指数函数单调性的逆用.

(5)回顾反思，提升素养

问题6我们是怎样研究指数函数的？

设计意图引导学生回顾指数函数的研究过程：提出问题、建立模型、研究模型、运用模型.

进一步引导学生回顾每个环节：怎样在具体情境中发现问题、提出问题？建立数学模型的一般过程与方法是什么？怎样研究数学模型？怎样运用函数模型解决问题？

进而让学生感悟：研究指数函数的基本过程与方法，也是研究函数的一般过程与方法，为以后研究新的函数奠定基础．

本节课力图实现“为表达世界而建模”的理念. 首先是精心设计问题情境，让学生感悟数学是从自然世界中来，构建数学模型研究，再回到自然世界中去. 这样，既有助于增强学生的创新意识，又有助于增强学生的实践意识. 概而言之，建模意识和能力是在有价值的问题情境及数学应用情境中得到激发和培育的. 其次是注重数学建模过程，重视培养学生能从实际问题中建立数学模型的能力，学会用数学的眼光观察世界. 本节课的目的就是要呈现给学生一个比较完整的研究指数函数的过程，为以后其他基本初等函数的学习树立标杆. 换言之，在教学中，数学概念和原理获得过程的价值，远远超过运用它去机械解题的能力. 知其然，还要知其所以然，过程往往比结果更重要. 第三是培养学生的数学思维习惯. 数学建模是对现实问题进行数学的抽象，用数学的思维分析，用数学语言表达，用数学方法构建模型解决问题的素养. 数学模型搭建了数学与外部世界联系的桥梁，是数学应用的重要形式. 数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力. 养成良好的数学建模的思维习惯，有助于学生今后的学习和发展，也是培养创新性人才的必备素养. 不仅要获得指数函数“是什么”，而且以“是什么”作为载体，通过探究“是什么”的“怎么做”的过程，知道“为什么”.