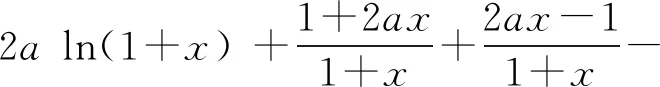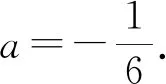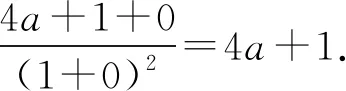大学视角下的中学数学(泰勒展开)

李尚志

(北京航空航天大学 100083)

例1(2018理科数学全国卷Ⅲ第21题)

已知函数f(x) = (2 +x+ax2) ln(1+x)-2x.

(1) 若a=0, 证明: 当-10 时,f(x)>0.

(2) 若x=0 是f(x) 的极大值点, 求a的值.

大学视角

(1)

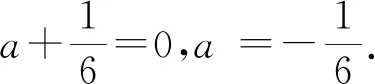
一般地, 设f(x) =f(c)+am(x-c)m+am+1(x-c)m+1+…是无穷级数且am≠0 是常数项之外最低次非零项的系数. 则当x→c时f(x)-f(c) = (x-c)m[am+am+1(x-c)+…]，方括号内的λ(x) =am+am+1(x-c)+…→am, 在c附近足够小的区间(c-d,c+d) 内, |x-c| 足够小,λ(x) 足够接近am, 正负号与am相同.f(x)-f(c)与m次项am(x-c)m正负号相同.

当m是奇数,x-c<0 与x-c>0 时f(x)-f(c) 的正负号相反, 一正一负,f(c)既不是极大值也不是极小值.

当m是偶数, 只要x-c≠0 都有(x-c)m>0. 当am<0 时都有f(x)-f(c)<0,f(c) 是极大值. 当am>0 时都有f(x)-f(c) > 0,f(c) 是极小值.

中学生只要背熟了泰勒展开式

中学解法

首先,f(x)=0.

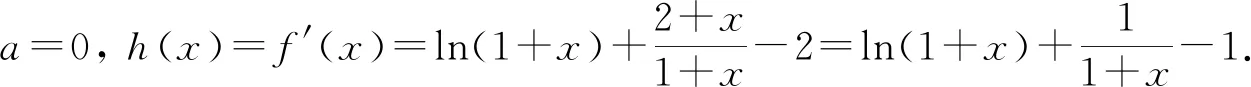
h(0)=0,

当x>0,h′(t)>0 对区间(0，x] 内所有t成立.h(t) 在区间[0，x]由h(0)=0 递增到h(x)=f′(x) > 0. 区间(0,x) 内所有f′(t)>0.f(t) 在区间[0,x] 内由f(0) 递增到f(x)>0. 这证明了f(x)>0 对所有x>0 成立.

当-10.

这说明f′(t)>0 对区间[-1,0) 内所有t成立,f(t) 在区间内单调递增到f(0)=0, 可知f(x)<0 对所有-1≤x<0 成立.

(2)f(x) 在定义域(-1,+∞) 有任意阶导数.f(0) 是极大值, 就是说0 附近某区间(-d,d) 内其它值f(x)

当x<0 到0,f(x) 由0, 令x→0得f′(0) ≥ 0.x=0 到x>0,f(0) 到f(x)

f′(0)=0, 且f″(x)<0 对0附近某区间内x≠0都成立, 这是f(0) 为极大值的充分必要条件.

计算得

f′(0)=0.

f″(0)=0.

f(0) 是极大值⟺在x=0 左右附近有g(x)=f″(x)<0=g(0),这又要求g(0) 是极大值, 必须g′(0)=0.

区间(-1,4) 内λ(x)>0,g′(x)=-xλ(x) 的正负号与x相反,在区间(-1，0) 内g′(x)>0, 区间(0，4) 内g′(x)<0.g(x) 在区间(-1，4) 递增到g(0)=0 再递减, 当x≠0 都有f″(x)=g(x)<0, 这与f′(x)=0 一起保证了f(0) 在(-1，4)内是最大值, 也是极大值.

第(2)小题解法2当x→0, 2+x+ax2→2>0. 0 附近足够小区间(-d，d) 内, 2+x+ax2足够接近2, 也有2+x+a2>0.f(x) 在区间(-d，d) 内的正负号与

相同.f(0) 是极大值⟺q(0) 是极大值⟺0 附近某区间(-h，0) 内

点评解法2的优点是: 先用除法将与ln(1+x) 相乘的2+x+ax2剥离, 只求一阶导数就把对数函数消去, 化成分式. 容易判定q′(x) 在x=0 附近取值的正负号, 不需要高阶导数, 也不需要再求极限.

(Ⅰ) 求a，b的值.

对函数f(x)计算得f(1)=b=1,

(Ⅱ) 题目要求当x>0 且x≠1 时

当x>0,x≠1, 由x+1>0，d(x)>0 得

当x→1 时上式左边的极限为h′(1)=-2k≥0, 必须k≤0.

当x>1,h(1)=0 单调递增到h(x)>0,

k的取值范围为(-∞，0].

本题函数d(x) 在x=1无意义, 无法由d(1)的值和区间(0,+∞)上的导数d′(x) 判定区间各点的d(x) 值. 乘x2-1 之后得到的h(x)在所有各点(包括x=1 ) 都有函数值和导数值. 而且导数h′(x) 不含对数函数. 将h(x) 在各点的值判断清楚了,d(x) 在x≠1 的各点的值也都清楚了.

借题发挥泰勒运筹, 求导实施

1. 举一反二. 具备了基础知识的考生都知道f(0) 是极大值的一个必要条件是f′(0)=0. 常规考试题一般都有f″(0)<0 来保证0 附近左右两边的f″(x)<0,f′(x) 左正右负, 从而保证f(0) 是极大值.本题却故意让f″(0)=0 来增大难度, 把只会用现成方法的考生刷下去, 帮助能够灵活运用现成方法的考生脱颖而出. 所谓“灵活运用现成方法”, 当然不是让你用泰勒展开, 也不是让你用洛必达法则, 因为泰勒展开和洛必达法则都不是现成方法, 而是新的知识和方法. 我不能猜测出题人希望你用哪一种现成方法. 我能想到的是: 当f″(0)=0, 如果二阶导数g(x)=f″(x) 在x=0 左右两边的取值g(x)<0 都为负,g(0) 又是极大值. 将f(0) 取极值的条件f′(0)=0 用到g(x) 身上得到g′(0)=0, 当g″(0)<0 就得到g(0)=0 是极大值, 从而f(0) 也是极大值. 这是将现成方法用两次, 可以叫做举一反二, 还不是举一反三.

假如认识到当x→0，

的极限就是函数f″(x) 在x=0 的导数f‴(0), 就不必费尽心机去求极限, 只要套公式求f″(x) 的导数就行了.

假如你不懂三阶导数, 或者怕使用了三阶导数被判为超纲而扣分.那很好办: 将二阶导数f″(x) 改个名字记为g(x), 忘掉它是二阶导数, 再求导数就变成一阶导数g′(0), 而没有三阶导数了. 甚至如果你对二阶导数都感到害怕, 可以将一阶导数f′(x) 记为h(x), 二阶导数f″(x)=h′(x) 就变成一阶导数了. 不需要学习新知识, 没有新困难.

3. 洛必达隐身避超纲

很多考生看不出当x→0 时

(2)

其实我很赞成中学老师这种观点: 中学生提前学了大学知识,只要用得正确, 就应该鼓励而不应该打击. 问题在于: 第一, 你用得正确吗?第二, 既然人家见了“洛必达”三个字就要扣分, 你难道就没有办法回避这三个字, 换汤不换药, 用中学教材上讲过的方法将极限求出来?

如果你真是“超纲”学会了大学微积分, 这两个问题都迎刃而解.

第一, 大学怎样求这个极限? 不是用洛必达法则, 而是

用的是微分学两个基本极限之一:

(3)

高考考生不是大学生, 不能按大学标准要求, 而应该按中学要求.中学生应该怎样来求这个极限呢? 中学教材没有讲e的基本极限, 更没有讲洛必达法则, 但是讲了导数公式, 也讲了导数定义. 就应该用导数定义和导数公式来求. 高考中是否准许用洛必达法则, 争吵了很多年, 纠结的几乎都是这“两个”极限

f(x)=lnx，

其实, 凡是可以用洛必达法则求极限的, 通通都可以用导数定义来代替, 洛必达三个字可以一律不用. 例如, 当x→0 时f(x)→0,f(x)除以x的商的极限

一般地, 当x→c两个函数f(x)，g(x) 都趋于0, 它们的比的极限

这就是用导数定义推出洛必达法则. 为了避免超纲扣分, 你不说它是洛必达法则, 自己用导数定义重新推出来, 不用洛必达之名, 只用中学允许的知识, 仍然将极限化成了导数. 例如, 当x→1 时求极限

虽然这样的题目难度超纲, 但如果真的遇到了, 以上解法只用了导数定义和导数公式, 没有出现洛必达三个字, 并没有超纲.

(未完待续)