解密数学抽象 探索教学策略①

张金良

(浙江省教育厅教研室 310012)

众所周知，抽象无处不在，抽象无处不有，在人们日常生活与教学活动中依据各自的理解被广泛使用着，比如“这个内容太抽象的”，“你用的方法太抽象了”，等等，但这里所说的抽象，仅仅是人们对抽象的一种通俗理解，把凭借生活经验不易理解的东西归结为抽象；但作为学术定义，它有一个明确的界定，“抽象”一词最早来自拉丁语中的“abstracio”，表示排除、抽取的意思.《辞海》中将“抽象”定义为：从许多事物中，舍弃个别的、非本质的属性，抽象出共同的、本质属性或特征的思维过程，由此可见抽象的过程是一个概括、分离和提取的过程.抽象是思维的基础，是对同类事物的刻画与构造.而数学抽象又有怎样的内涵与特点？数学教学实践活动又如何去培养呢？下面作深入的分析，供参考.

1 数学抽象的内涵及其相关概念

数学抽象是指舍弃事物的一切物理属性，得到一个数学对象的思维过程.它主要从数量与数量关系、图形与图形关系两方面抽象出数学概念及概念之间的联系，从事物与事物之间的联系、事物内部要素之间的联系中抽象出一般规律和结构，并用数学语言加以表征.通俗地讲数学抽象是通过观察、分析，撇开数学对象的外部的、偶然的、非数学的(物理的、化学的、社会的)东西，分析与提炼出其本质、内在、必然的东西，从空间形式和数量关系上揭示数学对象的本质和规律的一种数学研究方法．数学抽象素养是通过对具体而生动的数学问题进行分析与提炼，概括出一般结论，并应用于解决新的问题之中来体现.数学抽象反映了数学的本质特征，是数学六大核心素养的核心，贯穿于数学教学的全过程.

从内容上看，数学抽象包括数学概念、命题、方法和体系的抽象.其中数学概念的抽象是指通过抽象活动形成数学概念；数学命题的抽象是指通过抽象建立数学概念的因果关系，形成命题和规则；数学方法的抽象是指通过对数学操作程序的抽象，形成数学方法、数学思想和解决问题的策略；数学体系的抽象是指通过对概念、命题、方法和思想的抽象，建立概念、命题(规则)之间的普遍联系，形成数学体系.

数学抽象具有一些典型的特点.郑毓信在“数学抽象的基本准则：模式建构形式化原则”(《数学通报》，1990(11)：9-11)中认为数学抽象具有理想化、精确化、模式化的特点，李昌官在《数学抽象及其教学》文中，指出数学抽象具有纯粹性、精确性、理想化、模式化、形式化五个特点.两位学者已表述的很正确，本文吸收上述的观点，用更具体的语言再说说其特点：数学抽象具有高度概括，结论更具有一般性，表达简约、精确、能用数量化、符号化、公式化和图形化刻画.

数学抽象的类型很多，根据抽象对象的不同，数学抽象可分为性质抽象、关系抽象、等价抽象等.所谓性质抽象是指关于研究对象某一方向的性质或属性的抽象；所谓关系抽象是指关于研究对象的数量关系或空间位置关系的抽象，如直线与平面平行、平面与平面垂直是关系抽象的结果；等价抽象是按某种等价关系，抽取一类对象共同性质特征的抽象.自然数概念是等价抽象的结果，其本质是某类等价集合的标记，即集合间可以建立一一对应关系，它们是“对等”的．根据抽象方向的不同，数学抽象可分为同向与逆向思维的数学抽象，悖向思维的数学抽象与审美直觉的数学抽象.所谓同向思维的数学抽象，即延续已有的思维方向思考问题，它主要包括弱抽象和类比联想等方法；其中的弱抽象，也叫做“扩张式抽象”，是指对事物某一方面特征(或侧面)加以概括，从而形成比原对象更为一般的概念或理论的一种抽象方式．如“正方体→长方体→直平行六面体→直棱柱→斜棱柱”顺序进行的抽象就是弱抽象．弱抽象的特点是研究对象的外延不断扩大，内涵不断缩小，把结论推广到更一般的情形；逆向思维的数学抽象.指与原思维方向反向地思考与探究问题，它主要包括强抽象、精确化与完备化的思维方法．其中的强抽象，也叫做“强化结构式抽象”，是指通过扩大研究对象的特征，从而形成比原对象更为特殊的概念或理论的一种抽象方式．如按“斜棱柱→直棱柱→直平行六面体→正四棱柱→正方体”顺序进行的抽象就是强抽象．强抽象的特点是研究对象的外延不断缩小，内涵不断扩大，更深刻地认识事物某一方面的特征.悖向思维的数学抽象，即背离原来的认识并在直接对立的层面上探索新的发展可能性，是立体型的抽象.

2 数学抽象的教育意义

数学抽象是数学发展最基本的手段与方式，也是理性思维的主要特征之一，它贯穿于数学发生、发展和应用的各个过程之中，在数学的产生、发展与应用中起了不可替代的作用，使得数学成为高度概括、表达准确、结论一般、有序多级的体系.也正是数学抽象使人们获得数学概念和规则，提出数学命题和模型，形成数学方法与思想，认识数学结构与体系.

在数学抽象核心素养的形成过程中，通过积累从具体到抽象的活动经验，学生能更好地理解数学概念、数学命题、数学的方法和体系，能通过抽象、概括去认识、理解、把握事物的数学本质，能逐渐养成一般性思考问题的习惯，能在其他学科的学习中主动运用数学抽象的思维方式解决问题.因此，通过数学抽象的培养，学生可以很好地理解那些复杂的公式和定理，清楚这些公式和定理的来龙去脉，真正明白其中的含义，在更高的层面上理解数学知识的结构，更好地把握数学知识的本质属性，养成从更一般意义和方法上思考问题的习惯，提升概括抽象能力，促进理性思维的发展与提高.在数学学习过程中，学生只有具备了良好的思维水平和数学抽象素养，才能透过现象看到本质，这对学生来说不仅仅是一个获取知识的过程，也是一个探究发展的过程，对于学生的全面发展都有十分重要的作用和意义.

3 数学抽象的培养途径与方法

3.1 了解数学抽象的基本过程与方法

数学抽象的基本过程与方法前人已做过许多研究，其中徐利治认为，数学研究中的抽象思维过程基本上经历四个阶段：第一阶段主要研究数学现象问题；第二阶段主要是对各种具体数学属性进行分析，逐步去掉非本质属性；第三阶段，对于已经了解其结构的数学事实，确定其本质属性或特征；第四阶段，对基本上被确定的数学概念进行不断纯化.按照抽象的程度不同，史宁中把数学抽象分为简约阶段、符号阶段、普适阶段等三个阶段，其中简约阶段主要是把握事物在数量或图形方面的本质，把繁杂问题简单化、条理化，并清晰地表达；符号阶段主要是去掉具体内容，利用符号和关系术语，表述已经简约化的事物；普适阶段主要是通过假设和推理，建立法则、模式和模型，在一般意义上描述一类事物的特征或规律.

史宁中认为，抽象有两个层次，一个是直观描述，另一个是符号表达.他指出第一次抽象是有物理背景的，用自然语言表达的，这种抽象具体、直观，容易创造，但是也容易有反例；第二次抽象的特点是符号化，符号化的特点是挑不出毛病，严谨，但是抽象，没有物理背景.他建议老师在讲课时也必须讲第一次抽象，讲具体的背景，不要遨游于一大堆抽象的符号之间，要有感性认识，要建立起直观来，有了直观，才能判断.站在数学教学视角，按通常情况下学生学习时认知的先后顺序，浙江李昌官把数学抽象分为感知与识别、分类与概括、想象与建构、定义与表征、系统化与结构化[1]等五个阶段.事实上，数学抽象针对一个具体问题或对象，首先依据某一要素属性、进行区分、提炼、概括，使问题或对象变得明朗、简约和理想化，其次用数学符号进行表征，使问题或对象数学化，同时进行一般化，普适化，最后进行应用与系统化.最后，用逻辑方法建立概念之间的联系，形成概念系统.如概念体系，公理系统，新数学系统.

了解数学抽象的基本过程与方法是引导学生开展数学抽象的必要条件.在第一次抽象中教师要引导学生通过观察、类比、联想和结构分析，从中区分提炼出各种属性，并能建构出各种典型模型；在概括和普适化阶段中要求教师引导学生把典型模型一般化，通过类比、归纳和联想概括出一般化后的数学对象所具备的本质的公共的属性，并借助式子、图表等进行表示；在定义与符号化中，则重点要求表达准确、简约；在系统化阶段，则要根据学生的认知水平进行方向引领.

3.2 以数学概念形成教学为抓手，让学生学会数学抽象

章建跃在《树立课程意识落实核心素养》中提到：“众所周知，概念教学是数学教学的重中之重，而得出数学概念的过程是最典型的数学抽象的过程”.概念是思维的“细胞”，概念组成命题，命题形成判断，数学方法和思想是数学知识在更高层次上的抽象和概括.概念的形成过程是经历丰富的感性认识到深刻的理性认识的转变.在转变的过程中，需要经过多层次的分析、比较、抽象和归纳等加工.因此，概念的形成正是高度抽象和概括的过程，对概念的理解过程正是对这种抽象概括内容的剖析过程.在教学中，教师选取学生熟悉的典型实例，提供丰富材料，让学生经历一个完整的概念教学流程：辨别(刺激模式)→分化(各种属性)→类化(共同属性)→抽象(本质属性)→检验(确认)→概括(形成概念)→形式化(符号表达)，对比数学抽象的基本方法，熟悉数学抽象的“基本套路”，在概念形成的学习中学会数学抽象.从辨别到概括可视为第一次抽象，表现为用自然语言表达的直观描述；概括到形式化，完成符号表达为第二次抽象.比如在函数周期性教学时，首先可例举生活中大量的周期现象，如春夏秋冬四季轮回、海水涨落的潮汐、弹簧振子运动、摩天轮转动有共同特征，经过相同时刻所考察对象可重复出现，其次例举数学中的周期变化，如“数列an=1+(-1)n的项”、“f(x)=x-[x]图象”、“在直角坐标系uOv中，角x的顶点与原点重合，始边与Ou轴正半轴重合，终边与单位圆交于点P(cosx，sinx)．当角x的终边绕原点从Ou轴的正半轴开始，按照逆时针方向旋转时，点P的横坐标按照由1减少到-1，再由-1增大到1的规律连续地、周而复始地变化，纵坐标也有类似的变化规律”等，同样有一个共同特征，经过相同时刻后考察对象可重复出现，将其特征抽象直观描述函数经过不同的自变量值，函数值重复出现，实现第一次抽象，有了这些经验后，用严密的数学语言及f(x+T)=f(x)加以表征实现第二次抽象.

3.3 鼓励学生自主总结归纳，养成抽象概括的习惯

学生的数学抽象素养是从点点滴滴的细微处开始培养，是日积月累的潜移默化的过程.当我们上完一节课或者学习完一个章节时，教师就可引导学生对所学内容进行归纳总结.可用列表的方式归纳本章节的基础知识是什么，知识间的前后关联是什么，解题的思想方法是什么，解题要令是什么，也可以用画思维导图的方式寻找本章节知识点与数学思想方法相互间的联系.这种概括不但是对所学数学知识的复习与巩固，而且从中能锻炼学生对所学知识的提炼与概括能力，进而培养学生的数学抽象素养.例如学习完圆锥曲线可引导学生总结圆锥曲线是一门用代数方法研究圆锥曲线几何性质的一门学科，常见的较难题是求轨迹方程及与圆锥曲线有关的综合计算问题、范围问题、最大值最小值问题、是否存在问题、定点定值定向问题、对称问题、求证问题，解题常用方法有定义法、弦长韦达定理联用法、设而不求整体处理法、设参用参消参法、平面几何法等,事实上根据题型的通法解决问题是从一般到特殊的强抽象.因此，复习课、方法总结课是培养数学抽象素养的一类重要课型.

3.4 学会联想、推广、变式、类比等方法，掌握数学抽象的必要方法

教师在教授立体几何时可让学生类比平面几何的性质，教授等比数列时可类比等差数列，双曲线可类比椭圆，计数原理中分类和分步的类比等等，这不仅能提高学生的学习兴趣，还能给学生提供锻炼数学抽象概括能力的机会.例如在学习扇形面积、球体体积时，用类比思想让学生认识到圆面积公式与三角形面积公式，球体体积公式与锥体体积本质上都是分别相同的.事实上，借助极限思想，将圆周n等分，当n趋于无穷大时，每一等分可看成一个小三角形，这些三角形面积的和的极限就是圆的面积，由此可见，圆面积公式与三角形面积公式结构相同，抽象地看圆面积公式与三角形面积公式是一致的，是三角形面积公式的推广，同理球体体积公式可抽象成锥体体积的推广.

在教学过程中，教师可以通过一题多解，一题多变，多题一解，引导学生从不同思路、不同的视角认识问题，将同一问题抽象为不同的数学模型或经过多题一解抽象出一个模型，从中培养学生的归纳和概括的能力.例如函数教学时，可给出如下一组问题，引导学生概括.

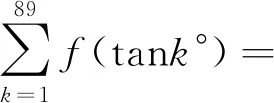
(4)(2012年全国高中数学联赛吉林初赛)方程2(x-1)sinπx+1=0在区间[-2,4]内所有解之和等于；

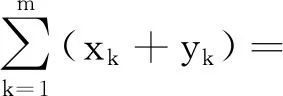
这样的题不胜枚举，但通过抽象概括，有一个共同规律是合理配对，对称求和.

开展数学建模活动，引导学生根据自身所处的生活环境，选择诸如池塘里浮萍增长问题、汽车与油耗问题、打球受伤吃药残留量问题、酒后何时可驾车问题、潮汐现象与轮船进港问题、摩天轮转动等有意义的实际问题进行加工提炼，抽象成数学模型，体验实际问题数学化过程，培养学生用数学知识解决实际问题的意识和能力.

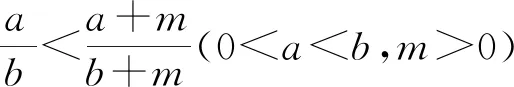
4 引导学生进行数学抽象的一个教学案例

案例摩天轮是一种大型转轮状的机械建筑游乐设施,游客坐在摩天轮的座舱里慢慢往上转时，可以从高处俯瞰四周景色.假定摩天轮的每一个座舱都在做同一匀速圆周运动．你能用一个合适的函数模型来刻画座舱(视为质点)距离地面的相对高度与时间的关系吗？

分析这是一个生活实例，首先将摩天轮抽象成一个几何图形，把这个生活实例变成一个数学问题，用数学语言抽述，实现第一次抽象，完成数学抽象的简约阶段.假设摩天轮的中心离地面的高度为h0，半径为r，座舱按逆时针方向以角速度ω匀速转动，座舱的初始位置P0处出发，某游客从图中P0经过时间ts时后到达P点，试求该游客离开地面的高度？

其次，探索上述各参数间相互关系，建立座舱P运动的数学模型，用数学语言表征，实现二次抽象，完成数学抽象的符号阶段.

如图1，以O为原点，以与地面AB平行的直线为x轴建立直角坐标系．设t=0时，座舱M位于点P0，以OP0为终边的角为φ，经过ts后运动到点P(x，y)．于是，以OP为终边的角为ωt+φ，并且有y=rsin(ωt+φ)．所以，座舱M距离地面的高度H与时间t的关系是H=rsin(ωt+φ)+h0．

再次，应用模型解决相关数学问题，进入数学抽象的普适阶段.

应用1如图2，设摩天轮的半径为1(单位长度)，摩天轮按逆时针做匀速转动，角速度为1rad/min(每分钟转动1弧度).假如你在摩天轮上的P点位置，若P点从图中P1点处开始计算时间．在如图所示的直角坐标系中，请问大家能否计算出在确定时间tmin时，你相对摩天轮中心的高度h(单位长度)．

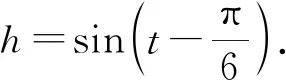
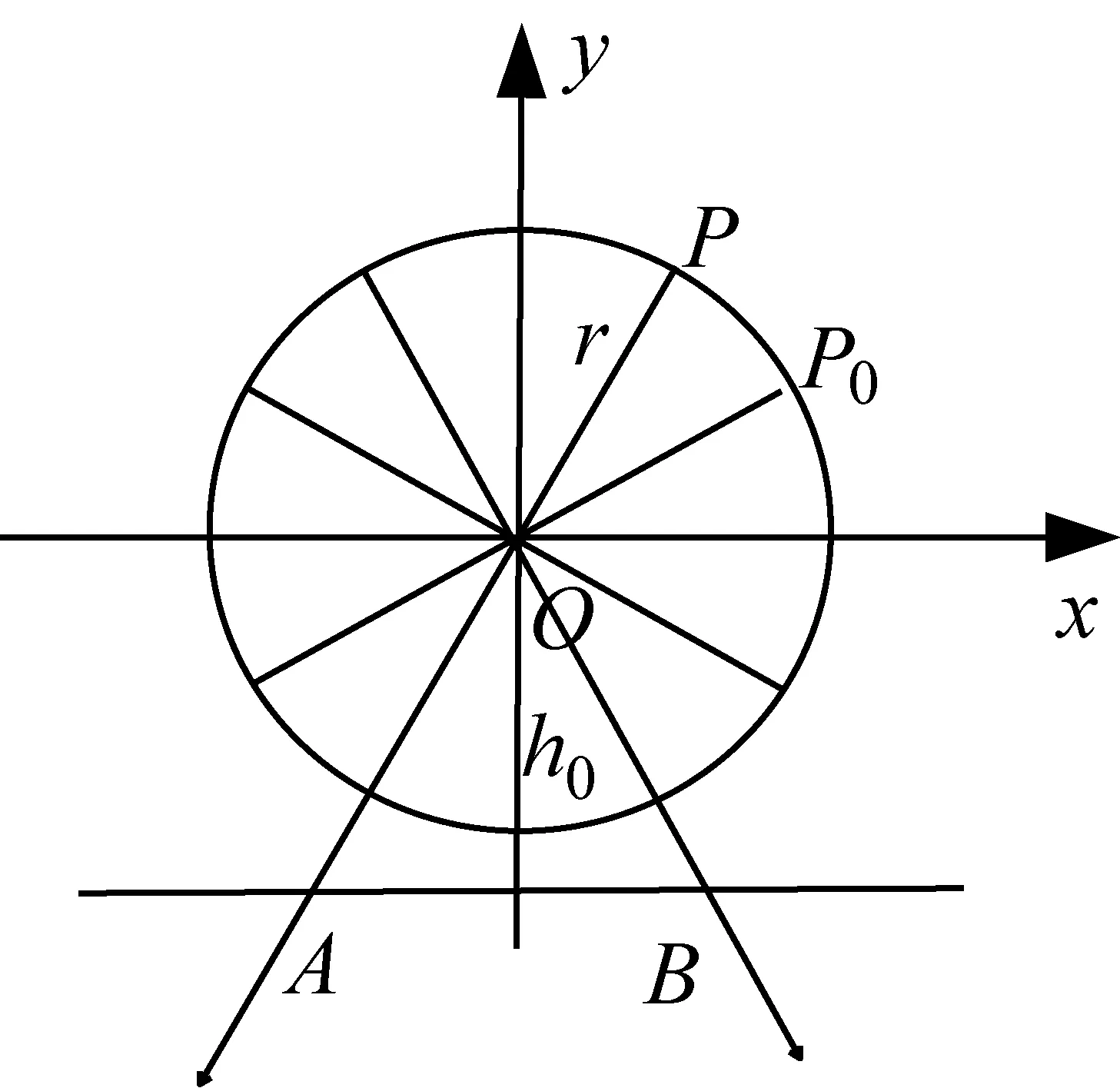
图1

图2

应用2某摩天轮最高点距离地面高度为120 m，转盘直径为110 m，设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要30 min．

(1)游客甲坐上摩天轮的座舱，开始转动tmin后距离地面的高度为Hm，求在转动一周的过程中，H关于t的函数解析式；

(2)求游客甲在开始转动5 min后距离地面的高度；

(3)若甲、乙两人分别坐在两个相邻的座舱里，在运行一周的过程中，求两人距离地面的高度差h(单位：m)关于t的函数解析式，并求高度差的最大值(精确到0.1)．

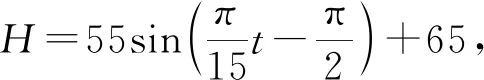
0≤t≤30；

(2)游客甲距离地面的高度

(3)甲、乙两人距离地面的高度差