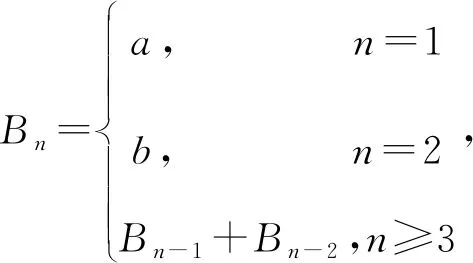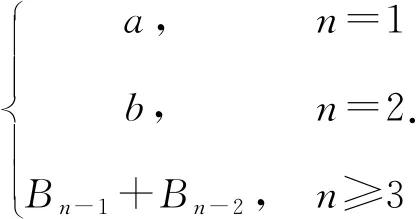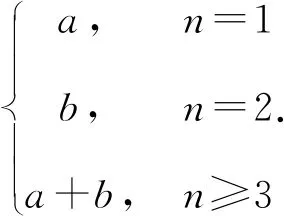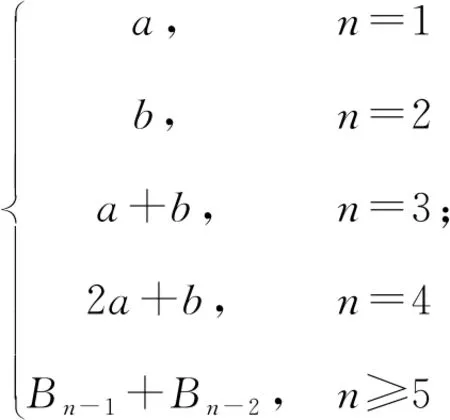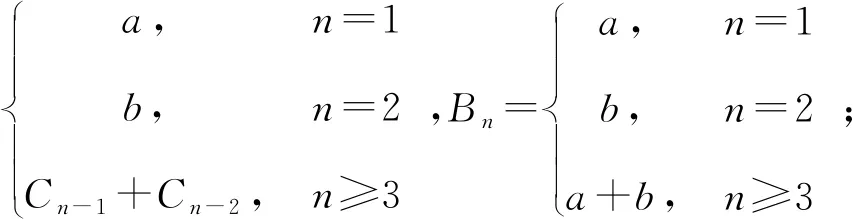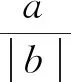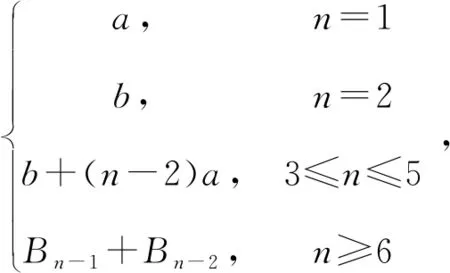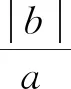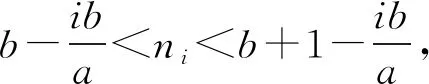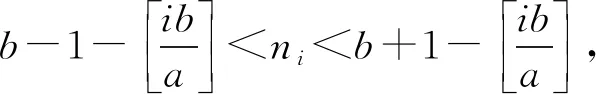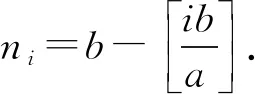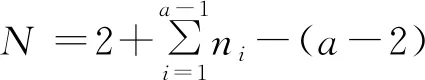斐波那契数列的推广与性质

胡 涛

(安徽省教育科学研究院 230061)

文[1]介绍了斐波那契数列及其推广形式的应用，受其启发，本文从斐波那契数列的定义出发，将其推广得到一类新的数列—F数列，并研究它的性质.

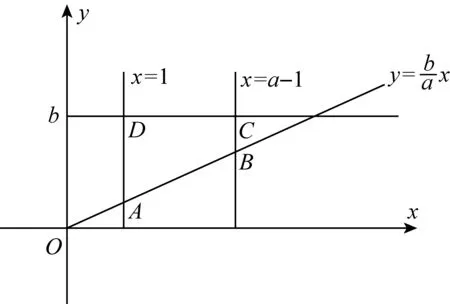
定义若数列{an}满足：对任意的n∈N*(n≥3)，总存在i,j∈N*，使an=ai+aj(i≠j,i

由数F列定义知斐波那契数列是其特殊情况，虽然它的通项公式不能确定，但an可由a1，a2线性表出，即有

定理1前两项为a1=a,a2=b的F数列{an}，则

an=pna+qnb,pn,qn∈N*(n≥3).

证明①n=3时，命题成立；

②假设n≤k时命题成立，

即ak=sa+tb，s,t∈N*；

当n=k+1时，ak+1=ai+aj(i≠j,i,j≤k)，

由归纳假设

ai=pia+qib，aj=pja+qjb(pi,pj,qi,qj∈N*)，

故ak+1=(pi+pj)a+(qi+qj)b，

即当n≥3时有an=pna+qnb,pn,qn∈N*.

推论前两项都为0的F数列{an}是零数列.

定理2首项为a1，公差为d的等差数列{an}是F数列的充要条件是d=a1.

证明(必要性)因为数列{an}是首项为a1，公差为d的等差数列，且是F数列，所以有a3=a1+a2, 即a1+2d=a1+a1+d,d=a1.

(充分性)若d=a1，则an=nd，由于当n≥3时，an=a1+an-1，1≠n-1,所以数列{an}是F数列.

定理4在前两项a1=a,a2=b(a,b>0)的F数列中，

证明设{an}是前两项为a1=a,a2=b的F数列，则B1=a1,B2=a2,B3=a1+a2.

(Ⅰ)若a≤b，

当n=3时，有B3=B1+B2,且B1≤B2

假设当n=k(n≥3)时，有Bk=Bk-1+Bk-2，此时有

B1≤B2

当n=k+1时，由于ak+1=ai+aj≤Bi+Bj≤Bk-1+Bk，故当ak+1=Bk+Bk-1时，ak+1最大,即Bk+1=Bk-1+Bk,所以对任意的n∈N*(n≥3)有Bn=Bn-1+Bn-2.故

由于b≥a>0，由定理1容易证明

(Ⅱ)若a>b，有

B3=B1+B2,且B2

当n=4时，由于a4=ai+aj(i≠j,i,j<4)，

a2≤a1

则a4=ai+aj≤a3+a2(i≠j,i,j<3)，

当且仅当a4=a3+a1时，a4最大，

即B4=a3+a1=b+2a，且B2

由于a5=ai+aj≤Bi+Bj≤B3+B4，

所以B5=B4+B3，且B2

假设当n=k(n≥5)时，Bk=Bk-1+Bk-2，

此时有

B2

当n=k+1时，由于ak+1=ai+aj≤Bi+Bj≤Bk-1+Bk，故当ak+1=Bk+Bk-1时，ak+1最大，即Bk+1=Bk-1+Bk,所以对任意的n∈N*(n≥5)有Bn=Bn-1+Bn-2，故

同(Ⅰ)可证

事实上，上面(Ⅰ)中的数列{Bn}是广义的斐波那契数列，Bn=afn-2+bfn-1(n≥3),其中fn是前两项f1=f2=1的斐波那契数列的通项公式.

类似的，若a1<0,a2<0，有

定理5在前两项a1=a,a2=b(a,b<0)的F数列中，

(Ⅰ)若a≥b，则

(Ⅱ)若a

定理6在前两项a1=a,a2=b(a>0,b<0)的F数列中，

证明设{an}是前两项为a1=a,a2=b的F数列，则易知B2

(Ⅰ)当a≥|b|时,由于a4=ai+aj≤Bi+Bj≤B1+B3, (i≠j,i,j<4)，所以B4=B3+B1=b+2a,且B2

同理B5=B4+B1=b+3a,B6=B5+B4,且B2≤B3

假设当n=k(n≥6)时，Bk=Bk-1+Bk-2,此时有

B2≤B3

则当n=k+1时，由于ak+1=ai+aj≤Bi+Bj≤Bk+Bk-1，所以Bk+1=Bk+Bk-1.

即对任意的n∈N*(n≥6)，都有Bn=Bn-1+Bn-2，故

依题设有

k|b|≤a<(k+1)|b|,(k∈N*)，

由于C2

所以C4=C2+C3=a+2b,且C2

同理C5=C4+C2=a+3b,…

Ck+2=Ck+1+C2=a+kb,

Ck+3=Ck+2+C2=a+(k+1)b,

Ck+4=Ck+3+C2=a+(k+2)b,

Ck+5=Ck+4+C2=a+(k+3)b,

且Ck+5

用数学归纳法可证明,当n≥k+6时，Cn=Cn-1+Cn-2，故

(Ⅱ)当a<|b|时，依题设有ka≤|b|<(k+1)a,k∈N*，仿照定理6(Ⅰ)的证明可得

在上面的定理中，我们看到数列{Bn}、{Cn}都是从某项开始单调递增或递减.易知前两项为a1=a,a2=b的F数列{an}单调递增的必要条件是0

出乎意料的是从第5项开始，Cn为连续的自然数.一般地，有

定理7在前两项a1=a,a2=b(a,b∈N*)的单调递增的F数列{an}中.若(a,b)=1，则存在N∈N*，当n≥N时，Cn为连续的自然数.

证明注意到(a,b)=1，记b=am+r

(1≤r≤a-1)，则

可证a+ir(moda)=0,1,…,a-1[2]是模a的完全剩余系.若这a个自然数又在长度为a的区间内，则必然是连续的a个自然数.

为便于理解，不失一般性，不妨设b=ma+1,m∈N*, 由于

C1=a,C2=b,C3=a+b,{an}单调递增，a4>a3，则C4=min{a3+a2,a3+a1}=C3+C1.

当Cn≤a+b时，因为Cn≡0,1(moda)，且C3+C2≤Ci+CJ≡2(moda)，i≠j,i

若Cn1

当Cn≤a+2b时，Cn≡0,1,2(moda)，且Cn1+1+C2≤Ci+Cj≡3(moda)，因此，

当a+2b

若Cn3

……

当Cn≤a+(a-1)b时，Cn≡0,1,…,a-1(moda)，且Cna-1+1+C2≤Ci+Cj≡a(moda)≡0(moda)，因此，当a+(a-1)b1)形的自然数.令N0=na-1+1,可知CN0,CN0-1,…,CN0-a+1是连续的a个自然数,取N=N0-a+1,则当n≥N时，Cn=CN+n-N,故Cn为连续的自然数,且CN=CN0-a+1=ab+1.

推论前两项a1=a,a2=b(a,b∈N*,a

定理7中最小的N值可以这样确定:先计算[a,a+ab)中{Cn}的项数，这些项是由a,b和首项为a+ib，公差为a的等差数列{pni}(i=1,2,…,a-1)的项构成的.

因为pni=a+ib+(ni-1),

如图，由几何意义[2]可知

下面我们解决如下问题：

已知{an}是F数列，且单调递增，a1=3,a2=5.若an=2018,求的n最大值.

解当an=Cn=2018时，n最大.由于

C3=8,C4=11,C5=13,C6=14,C7=16,

C8=17,C9=18.

当n≥7时,Cn=16+(n-7)，

由Cn=2018得,n=2009.

下面证明n的最大值为2009:

因为an≥Cnn∈N*,C2009=2018,

则a2009≥C2009.

若an=2018,则a2009≥an,n≤2009.

故n的最大值为2009.

一般地，有

定理8已知{an}是F数列，且单调递增，a1=a,a2=b(a,b∈N*,b>a).若an=k(k∈N*,k>ab),则当an=Cn=k时，n最大.

类似地,还有

定理9已知{an}是F数列，a1=a,a2=b(a,b∈N*,b>a).若an=k=BN.则当n=N时，n最小.