需求价格弹性系数定义和不同需求价格弹性与对应需求曲线不匹配问题及修正

吕宁

（曲靖师范学院，云南 曲靖 655007）

在物理学上，弹性是指物体在外力作用下发生形变，继而，当外力撤消后能恢复原来大小和形状的性质。另外，弹性还表示事物的可多可少、可大可小等伸缩性。

一、弹性理论发展概略

经济学上的弹性概念是由阿尔弗莱德·马歇尔提出来的。在他的《经济学原理》[1]中写到：“我们已经知道，关于一个人对一样商品的唯一的普遍规律就是：如果其他情况不变，这种欲望每随他对这商品的所有量的增加而递减。但是，这种递减也许是缓慢的，也许是迅速的。如果它是缓慢的，则他对这商品所出的价格，就不会因为他对这商品的所有量的大量增加而下降很大；而且价格的小跌会使他的购买量有较大的增加。但是，这种递减如果是迅速的，价格的小跌使他的购买量只有很小的增加。在前一种情况下，他愿购买此物的心理在一个小的引诱的作用下而大大扩展：我们可以说，他的欲望的弹性大。在后一种情况下，由于价格的下跌所造成的额外引诱，没有使他的购买欲望有任何扩大：也就是他的欲望弹性小。一个人的需要是如此，整个市场的需要也是如此。我们可以一般地说：市场中需求弹性（或感应性）的大小，是随着需要量在价格的一定程度的下跌时增加的多寡，和在价格的一定程度的上涨时减少的多寡而定的。

我们可以说，如果价格的小跌会使需要量有相同的按比例的增加，则需求弹性是1；或者我们可以概略地说，如果价格下跌1%会增加销售1%，则需求弹性是1；如果价将下跌1%使需要量分别增加2%或0.5%，则需求弹性是2或0.5，以此类推。”

萨缪尔森在《经济学》中，写到：“价格弹性的准确定义是需求变动的百分比除以价格变动的百分比。用ED表示（需求的）价格弹性，并且为了方便起见，我们去掉负号，让所有的弹性都表现为正值。”他还进一步明确了富有需求价格弹性、缺乏需求价格弹性和单位需求价格弹性的概念。

经过后来的经济学家的发展，增加了需求的收入弹性和需求的交叉价格弹性理论等内容，弹性理论已成为微观经济学理论中的一个重要组成部分。

二、主流观点中的弹性理论

弹性的概念可以应用在所有具有因果关系的变量之间，作为原因的变量通常称作自变量，受其作用发生改变的量称作因变量。弹性是指因变量对自变量变动的敏感程度（或反应程度），或者自变量对因变量变动的影响程度。弹性可以用弹性系数大小来衡量。

在经济学中，弹性系数的一般公式为：弹性系数=因变量的变动比例/自变量变动比例。

用数学方式来表达就是：如果自变量x和因变量y之间存在关系y=f（x），则y对x的弹性系数：e=（吟y/y）/（吟x/x）。

发展到目前的阶段，经济学中常见的弹性有：

第一，需求的价格弹性。需求的价格弹性是指需求量变动对价格变动的敏感程度（或反应程度）。需求价格弹性系数=需求量的变动比例/价格变动比例。

第二，供给的价格弹性。供给的价格弹性有时候也被简称为供给弹性。供给的价格弹性是指供给量变动对价格变动的敏感程度（或反应程度）。供给价格弹性系数=供给量的变动比例/价格变动比例。

第三，需求的收入弹性。需求的收入弹性是指需求变动对收入变动的敏感程度（或反应程度）。需求收入弹性系数=需求量的变动比例/收入变动比例。

第四，需求的交叉价格弹性。需求的交叉价格弹性是指需求量变动对相关商品价格变动的敏感程度（或反应程度）。需求交叉价格弹性系数=需求量的变动比例/相关商品价格变动比例。

另外，弹性理论还包括弹性系数的计算以及通过弹性系数的不同数值，而对相关的经济现象进行判断等内容。需求的价格弹性理论作为最重要的弹性理论，还对需求的价格弹性进行了分类，对每一类别的需求价格弹性都给出了对应的需求曲线，部分具体内容见下文。

但是，需求价格弹性系数的定义和计算公式的实际意义解释以及分类型的需求价格弹性的需求曲线表达存在问题。接下来的部分，分析这些存在的问题，并给出修正的建议。

三、需求价格弹性理论存在的问题及修正

（一）需求价格弹性系数定义及公式解释存在的问题及修正

1.需求价格弹性系数定义存在的问题及修正

主流观点采用以下公式计算需求的价格弹性：

需求的价格弹性系数=-需求量变动的百分比/价格变动的百分比

用字母表示为：Ed=-（吟Q/Q）/（吟P/P），其中Q表示需求量，P表示价格，吟Q表示需求改变量，吟P表示价格改变量。

这个计算公式不符合弹性系数计算公式的一般形式e=（吟y/y）/（吟x/x），在其前面多了一个负号，这不符合弹性概念的一般内涵，自然也不在弹性概念的外延之内。主流观点为加负号给出的理由是，一般情况下，吟Q和吟P符号相反，因此（吟Q/Q）/（吟P/P）为负数，为了便于比较，使比值为正数，所以在前面加了一个负号。

但是，吟Q和吟P的符号相反正是经济变量相互关系的真实反映。而且负值并不影响比较，也不影响对于经济现象的解释。负数小的，绝对值大，表明需求对价格变化敏感度较高；负数大的，绝对值小，表明需求对价格变化敏感度较低。

而且在需求的收入弹性和需求的交叉价格弹性的相关内容中，在弹性为负值时，并没有在其前面加上负号，而且这种负号正是对相关内容判定的依据。比如，需求的收入弹性为负数时，表明了该种商品是低档商品；在需求的交叉价格弹性系数为负值时，表明两种商品之间的关系是互补关系。

而且需求价格弹性系数本身，其值也是分为正负的。吉芬物品的价格变化和商品需求量的变化是同一方向的，也就是说，对于吉芬物品来说，Ed=（吟Q/Q）/（吟P/P）是个正数，套用Ed=-（吟Q/Q）/（吟P/P）这个公式，那么按照主流观点的逻辑，似乎就无法比较大小了。

所以，需求的价格弹性系数公式应该改为，Ed=（吟Q/Q）/（吟P/P）

即，需求的价格弹性系数=需求变动的比例/价格变动的比例

对于需求价格弹性为负的，如果一定要在其前面加负号的话，必须说明是取绝对值，即：|Ed|=-（△Q/Q）/（△P/P）。需求的价格弹性是价格弹性，需求的价格弹性的绝对值是需求的价格弹性的绝对值，不能模糊和混淆。

2.需求价格弹性系数计算公式及实际意义解释方面存在的问题及修正

还存在一个问题，即对于Ed=-（吟Q/Q）/（吟P/P）的解释，很多著作中将其转为文字表达时，是这样的：需求的价格弹性系数=-需求量变动的百分比/价格变动的百分比。并且认为，需求的价格弹性系数的实际意义是，价格变动一个百分点，所引起的需求量变动的百分点数。暂不考虑其加了负号的错误，即使只考虑负号后面的内容，也不能如此解释。

首先，△Q/Q和△P/P分别只表示普通的比例，并没有转化成百分数，因此将△Q/Q解释为需求量变动的百分比，将△P/P解释为价格变动的百分比是不准确的，对于（△Q/Q）/（△P/P）的解释自然同样不准确。进一步地，相应的实际意义更不能表述成价格变动一个百分点，所引起的需求量变动的百分点数。

通过下面的一个实际例子，来证明上述传统观点的错误。

在某市场上，最初的价格P=500，需求量Q=100；由于某种原因，价格下降为400，需求量增加至150。

本例中，需求的价格弹性Ed=-（△Q/Q）/（△P/P）=[（150-100）/100]/[（400-500）/500]=（1/2）/（-1/5），1/2和1/5可以转化成百分比，但是这个公式并没转换，所以也就不存在价格变化百分之一需求量变化多少个百分比的解释。但是，如果进行了向百分比的转化，情况则发生了变化。

将Ed=-（△Q/Q）/（△P/P）=（1/2）/（-1/5）进行转化，分子分母同乘以100%，则Ed变化为50%/20%=2.5，这时，才可以将需求的价格弹性的实际意义表述为价格变动一个百分点，所引起的需求量变动的百分点数。

这个乘以100%的过程不能省略。如果乘以1 000‰，则Ed变化为500‰/200‰=2.5，这时的实际意义就要表述为价格变动1‰，所引起的需求量变动的千分点的个数。所以Ed=-（△Q/Q）/（△P/P）并不直接意味着价格变动一个百分点，所引起的需求量变动的百分点数。

（二）不同类型需求价格弹性对应的需求曲线不能准确表达其特性的问题及修正

主流观点根据商品需求的价格弹性大小的不同，把需求价格弹性分为5类[2]：

第一类，需求对于价格变化完全无弹性。需求价格弹性系数等于零的情况，即Ed=0①此部分内容为主流观点，实际上Ed应该为|Ed|。，它表示无论价格如何变动，需求量都不会变动。

第二类，需求对于价格变化缺乏弹性。需求价格弹性系数小于1的情况，即Ed＜1，它表示需求量的变动率小于价格的变动率。

第三类，需求对于价格变化具有单位弹性。需求价格弹性系数等于1的情况，即Ed=1，被称之为需求单位弹性，它表示需求量的变动率与价格的变动率相等。

第四类，需求对于价格变化富有弹性。需求价格弹性系数大于1的情况，即Ed＞1，它表示需求量的变动率大于价格的变动率。

第五类，需求对于价格变化具有完全弹性。需求价格弹性系数趋于无穷大的情况，即Ed→∞，它表示当价格为既定时，需求量是无限的，或需求量的变动是任意的。价格上涨，需求量减少为0，价格下降需求量无限增大。

这种分类使弹性理论更加完整，在实践中，也具有较强的指导意义。但是，传统观点给出的具有上述需求价格弹性的需求曲线的形状在反映其所对应的弹性特征方面却存在一些问题。其中，完全无弹性的需求曲线和单位弹性的需求曲线形状符合所对应的弹性特征，其余三种需求曲线和各自对应的需求价格弹性特征不相符合。

1.完全无弹性①此处完全无弹性是指需求对于价格的变化完全无弹性，下文中的缺乏弹性、单位弹性、富有弹性和完全弹性同样省略了“需求对于价格的变化”这几个字。

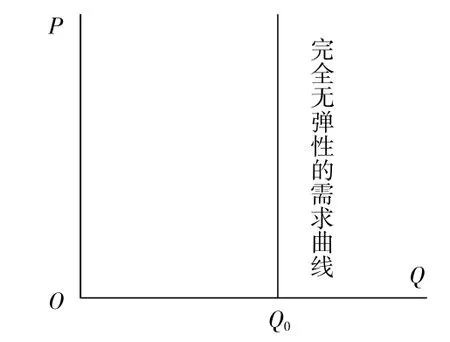
图1

图1中的垂直于横轴的需求曲线，被界定为完全无弹性，这种表达是正确的。

如果弹性绝对值为0，由公式|Ed|=-（△Q/Q）/（△P/P）②由此处开始，根据本文的观点，将|Ed|和Ed区分使用。，可知是由于△Q=0造成的。△Q=0可以推出△Q/Q=0，因此由|Ed|=0可以推出斜率为0，斜率为0的直线平行于自变量轴。反推过来，如果给出的需求曲线是平行于P轴的，那么其斜率△Q/△P=0，可推出|Ed|=-（△Q/Q）/（△P/P）=0。斜率为0和弹性（或其绝对值）为0是等价的，垂直于横轴的需求曲线上各点的需求对于价格是完全无弹性的。

2.缺乏弹性

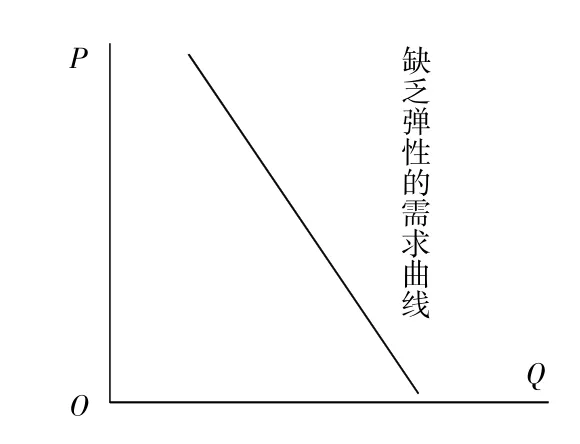
图2

图2中，主流观点认为，这条陡峭的需求曲线用来表示该条需求曲线上各点处需求对于价格变化缺乏弹性。这种说法是不准确的。结合下面几个图来进行分析。

首先，对平缓和陡峭的直线进行界定。

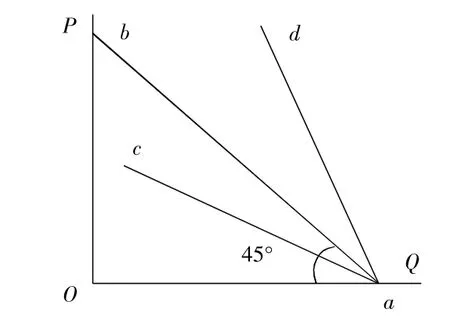
图3

如图3所示，直线ab和横轴负方向和纵轴正方向所形成的角度均为45°，绕着ab和横轴的交点a对ab进行逆时针旋转，所得到的直线ac与横轴负方向所形成的夹角小于45°，与ac平行的直线是平缓的。将直线ab绕着其和横轴的交点a进行顺时针旋转，所得到的直线是ad，ad与横轴负方向所形成的夹角大于45°，与ad平行的直线是陡峭的。当然也可以绕着b点旋转而得到平缓和陡峭的需求曲线。

其次，要运用点弹性的几何意义来分析这条陡峭的需求曲线上弹性的变化。因此，还要介绍需求曲线点弹性③实际应为点弹性绝对值，为了便于读者和以前的知识衔接，暂时沿用了传统习惯说法，在接下来的内容中，用点弹性的绝对值取代点弹性。的几何意义。通过图4进行分析。

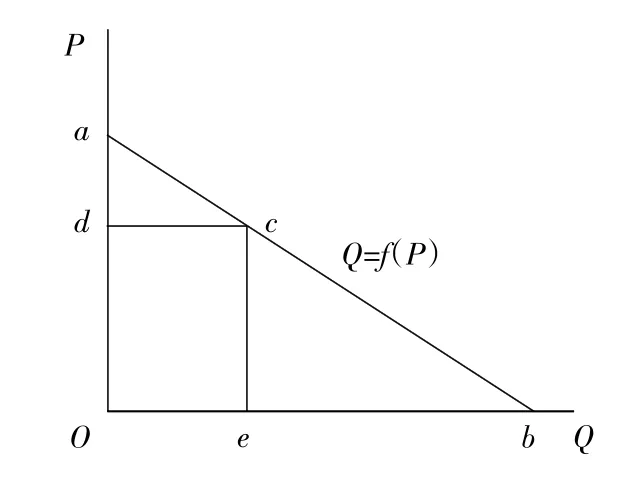
图4

C点为需求曲线上的任何一点，其价格弹性绝对值为：

|Ed|=-（dQ/Q）/（dP/P）=-（dQ/dP）*（P/Q）=（eb/ce）*（ce/oe）=eb/oe=cb/ac=do/ad

根据上述分析和理论，分析图5中陡峭的需求曲线ab上各点的需求价格弹性绝对值。取线段ob的中点，做平行于纵轴的直线，和ab相交于d点，根据点弹性绝对值几何含义，则可得出d点的需求价格弹性绝对值是1。d点左上方ab上的点的需求价格弹性绝对值大于1，d点右下方ab上的点的需求价格弹性绝对值小于1。

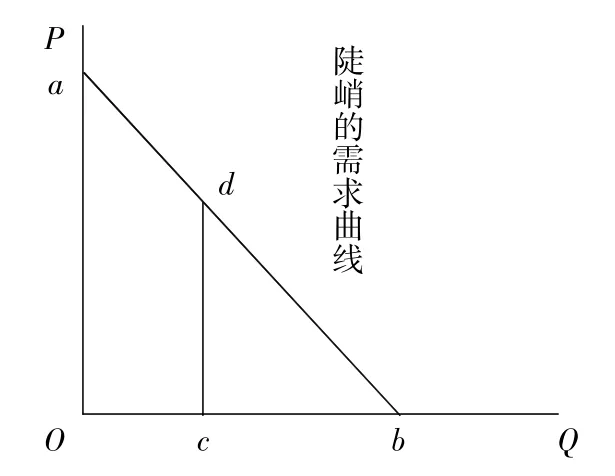
图5

3.单位弹性

图6所示的这种需求曲线符合单位弹性绝对值的性质。通多等轴双曲线的性质，易于证明，过程省略。

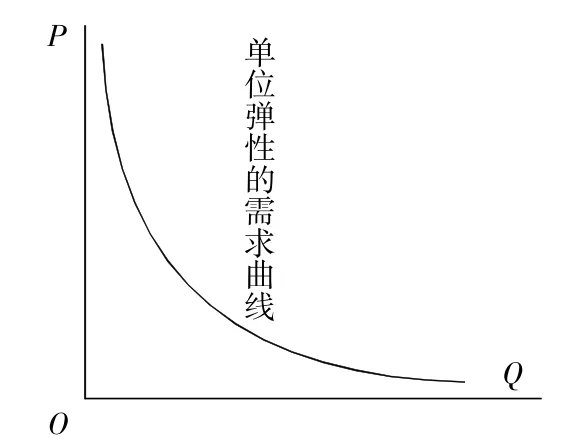
图6

4.富有弹性

主流观点下的富有弹性的需求曲线如图7所示，是一条平缓的需求曲线。

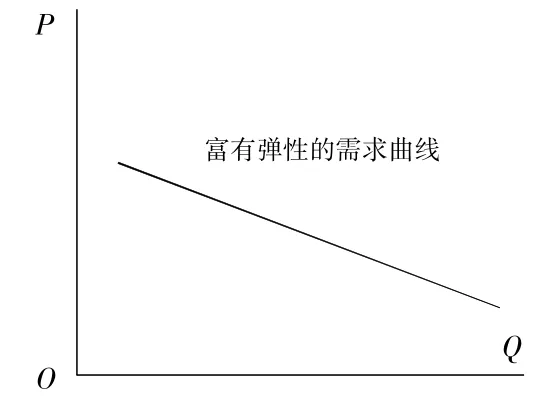
图7

但是这种表达是不准确的的。结合图8，进行说明。

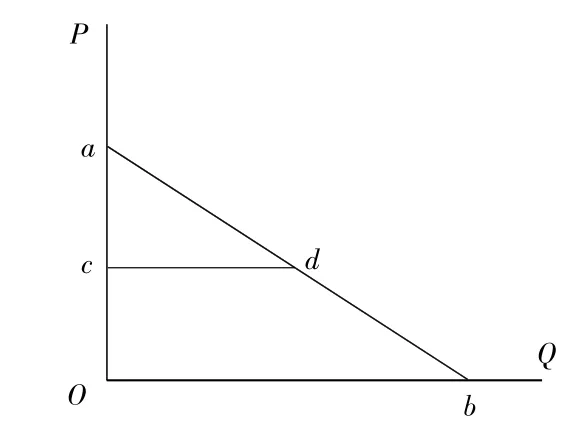
图8

根据线性需求曲线点弹性绝对值的性质，取oa的中点c，过c点做平行于Q轴的直线，交ab线于d点，则d点是线段ab的中点。d点的需求价格弹性绝对值是1。d点左上方ab上的点的需求价格弹性绝对值大于1，d点右下方ab上的点的需求价格弹性绝对值小于1。

传统观点所述的富有弹性和缺乏弹性的需求曲线的弹性绝对值分布情况，均为富有弹性和缺乏弹性各占一半，并均存在一个具有单位弹性的点。所以传统观点中的缺乏弹性和富有弹性的需求曲线上缺乏和富有弹性的特点不存在，因此，将陡峭的需求曲线界定为缺乏弹性，将平缓的需求曲线界定为富有弹性说服力是不足的。只能说，在横坐标和纵坐标单位相同的情况下，在相同的价格条件下，平缓的需求曲线上的点的需求价格弹性绝对值一般会大于陡峭的需求曲线上点的需求价格弹性绝对值。而不能将需求或陡峭的需求曲线从整体上对其弹性情况作出界定。

5.完全弹性

图9

图9是传统观点给出的需求对于价格变化具有完全弹性的需求曲线。这样的需求曲线并不能准确地表达出需求对价格具有完全弹性的性质。根据完全弹性的含义，价格上涨的话，需求量会降为0，价格如果下降，需求量会升至无穷大。而在图9中，根据所给出的需求曲线，如果价格上涨，由高于现有价格的位置引出平行于横轴的直线，并不能找到对应的需求量，而价格下降时，由低于现有价格的位置引出平行于横轴的直线，也不能找到对应的需求量，因此，必须给出新的需求曲线来反映需求对于价格具有完全弹性的性质。给出的新的需求曲线如图10所示。

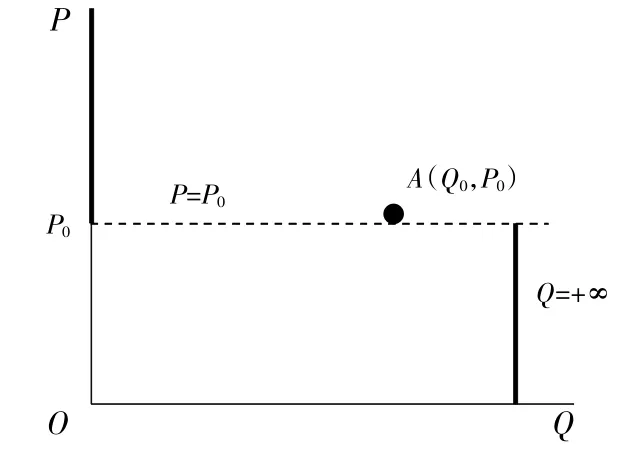
图10

图10给出的需求曲线是一个分段函数，符合需求对于价格具有完全弹性的性质①图10中P=P0这条虚线表示的需求曲线是主流观点下的具有完全弹性的需求曲线。。先看价格上涨时本需求曲线的解释力，价格高于P0时，本需求曲线是纵轴上（P0，+∞）这一段。实际含义是，只要价格大于P0，需求量就为0，也就是说，无论价格上涨到哪个位置，需求量降为0，这体现了完全弹性的性质。再看价格下降时本需求曲线的解释力，需求曲线在价格为（0，P0）这一区间时，是平行于纵轴的直线Q=+∞的一段。这表明当价格从P0位置开始下降时，无论下降到哪个位置，对该商品的需求量增加到无限大。而在现行的价格P0下，对应的需求量是Q0，而且Q0是在P0价格下，唯一可能的需求量，这一段的需求曲线表现为一个点A（Q0，P0）。

四、结论

本文通过对于传统需求价格弹性理论的剖析，指出需求价格弹性系数定义存在的问题。继而，进一步指出需求价格弹性系数公式的文字解释及这一解释的实际意义存在的问题。本文还对不同的需求价格弹性对应的需求曲线进行了分析，指出了缺乏弹性、富有弹性和完全弹性的需求曲线没有完全体现出各自所应反映出的弹性特点。除了指出存在的问题外，还给出了修正的方案。希望能为完善经济学中的弹性理论提供自己的一些想法。