Heisenberg李代数自同构群的结构
张 彦,任 斌
(苏州科技大学 数理学院,江苏 苏州 215009)
在李代数中,自同构是其结构理论研究的重要部分,它反映了该代数结构的对称性。研究者们对此做了大量的研究工作[1-16]。Heisenberg 李代数在李代数中占有非常重要的地位,2007 年张海山等对Heisenberg 李代数的自同构进行了研究,在文献[9]中作者针对Heisenberg 李代数的两种定义形式,分别讨论了在定义1形式下的自同构的充要条件,在定义2 形式下自同构群的结构。但对定义1 形式的自同构群的结构作者没有做进一步探讨。在文献[14]中作者对定义2 形式的Heisenberg 李代数(及Heisenberg 李超代数)的自同构群进行了探讨,得到了自同构群的若干子群。笔者对定义1 形式的Heisenberg 李代数的自同构群的结构做了进一步的研究,利用充要条件的结论,刻画了5 维Heisenberg 李代数自同构群的分解结构。由于7 维及以上的Heisenberg 李代数自同构群的分解结构更加复杂,还有待于研究者做进一步探讨。
文中所讨论的都是复数域上的Heisenberg 李代数。
1 基本概念和性质
定义1[16]设N 是域F 上的李代数。若φ 为李代数N 到自身的可逆线性变换,又满足

则称φ 为N 的自同构。N 的所有自同构构成一个群,称为N 的自同构群,记作Aut(N)。
定义 2[9]设 N 是以 e1,e2,…,en,en+1,en+2,…,e2n;c 为基底的复向量空间,在 N 中定义李运算[ei,en+k]=δikc,其他基底元素的李运算为0,线性扩充后,则N 关于所定义运算作成一个李代数,称为Heisenberg 李代数。
引理1[6]若N 是一个幂零李代数,则下面两个命题等价:
(1){x1,x2,…,xn}是 N 的一个极小生成元系;
(2){x1+N2,x2+N2,…,xn+N2}是向量空间 N/N2的一个基,这里 N2=[N,N]。
引理2[8]设x1,x2,…,xn为二步幂零李代数N 的一组基,φ 是N 上的一个可逆线性变换,则φ 是自同构当且仅当 φ[xj,xk]=[φ(xj),φ(xk)],1≤j,k≤n。
2 自同构的充要条件
设 N 是一个 Heisenberg 李代数,e1,e2,…,e2n;c 是 N 的一组基,且 c 是 N2的基。由[ei,ej]=Eijc,1≤i,j≤2n,有
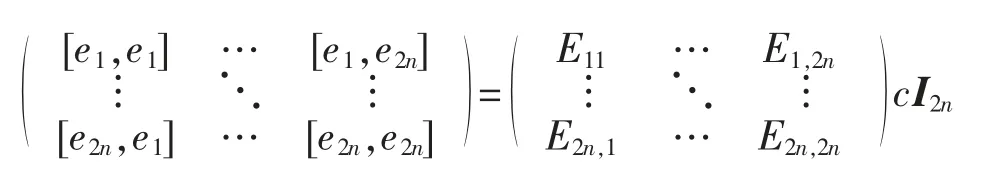
这里 I2n表示 2n 级单位矩阵。记 E=(Eij)2n×2n,显然
设 φ 是 N 上的一个线性变换,则有 φ(e1,e2,…,e2n;c)=(e1,e2,…,e2n;c)W(2n+1)×(2n+1)。
定理1N 的一个线性变换φ 是自同构当且仅当矩阵W 满足以下条件:
证明(必要性)由于 c=[e1,en+1],所以 φ(c)∈N2。从而于是有|A2n×2n|×k≠0。
因为φ 是N 的一个自同构,所以有

又因为[ei,ej]=Eijc,因而


于是有ATEA=kE。
(充分性)显然 φ 可逆。由必要性的证明过程易证(1)式成立,即 φ[ei,ej]=[φ(ei),φ(ej)],∀ei,ej∈N。又显然有 φ[ei,c]=[φ(ei),φ(c)],∀ei∈N,c∈N2。故由引理 2 知 φ 是 N 的一个自同构。
3 自同构群的结构
下面利用上述充要条件来研究5 维Heisenberg 李代数自同构群的分解结构。
设φ 是5 维Heisenberg 李代数N 上的一个自同构,有
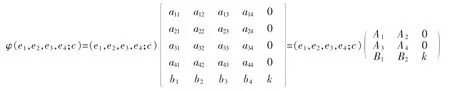
这里 Ai表示 2 级矩阵,Bi表示 1 行 2 列矩阵。

定理 2Aut(N)=GAGI,|GA∩GI|=1,其中且 GI,GA是 Aut(N)的子群。
证明由定理 1 易知 GA是 Aut(N)的子群。显然 GI⊆Aut(N),∀α1,α2∈GI,有

所以 α1α2∈GI。易知 α1α2=α2α1。
为了讨论GA的结构,需要下面的引理。
首先,由于ATEA=kE,即有下列等式

引理3设则 G3,G4是 Aut(N)的交换子群。
证明由于
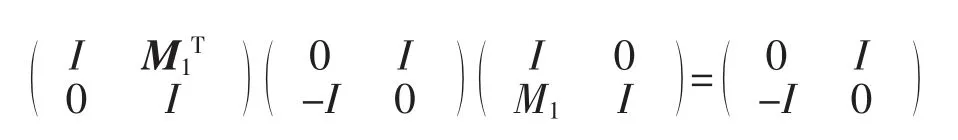
根据定理 1 知 G3⊆Aut(N)。∀β1,β2∈G3,有
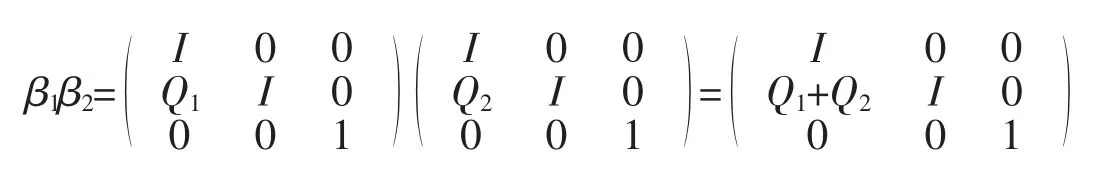
所以 β1β2∈G3,易知 β1β2=β2β1。
引理4设

则 G2,G5是 Aut(N)的子群。
证明显然 G2是 Aut(N)的交换子群。由于
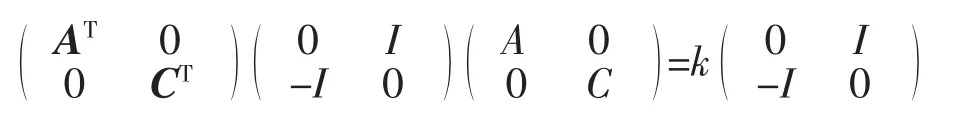
根据定理 1 知 G5⊆Aut(N)。∀η1,η2∈G5,有

所以 η1η2∈G5。
定理 3GA=G5G4G2G3G4G5G2。
证明
情形 1|A1|≠0
注意到
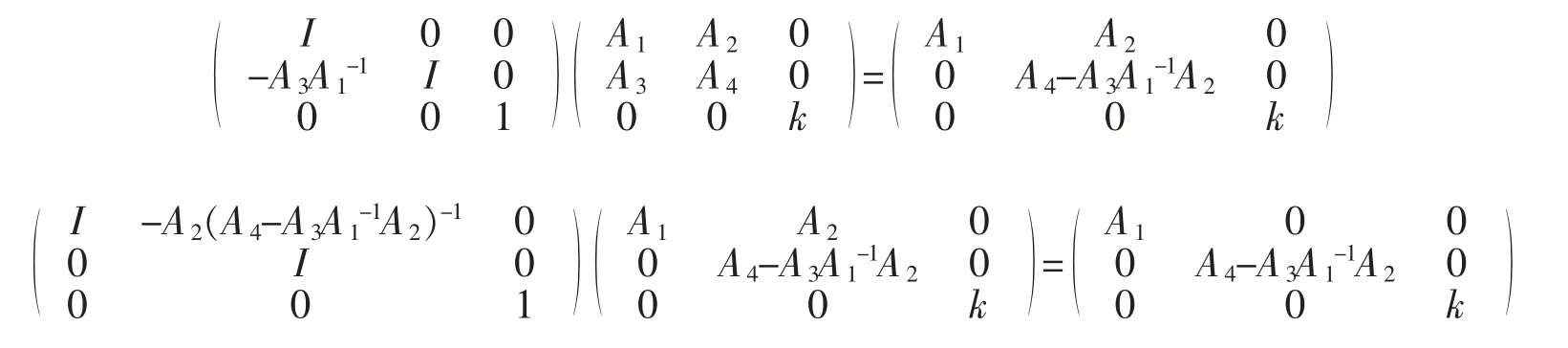
于是可知,对任意满足情形 1 条件的 φ∈GA,存在 φ3∈G3,φ4∈G4,φ5∈G5,使得 φ4φ3φ=φ5,从而 φ∈G3G4G5。
情形 2若 |A1|=0,A2,A3,A4中有一个是可逆的。
此时可通过初等变换归结到情形 1。当|A3|≠0 (|A2|≠0 类似可证),由于

对任意满足情形 2 条件的 φ∈GA,且|A3|≠0,存在 φ2∈G2,使得 φ2φ∈G3G4G5,从而 φ∈G2G3G4G5。
当|A4|≠0,由于
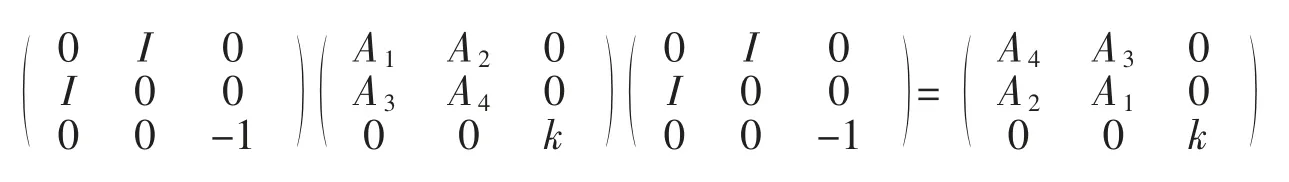
对任意满足情形 2 条件的 φ∈GA,且|A4|≠0,存在 φ2∈G2,使得 φ2φφ2∈G3G4G5,从而 φ∈G2G3G4G5G2。
情形 3A1,A2,A3,A4均不可逆。
易知 Ai≠0,i=1,2,3,4。由 A1的秩为 1 知存在可逆矩阵 P1和 T1,使从而有
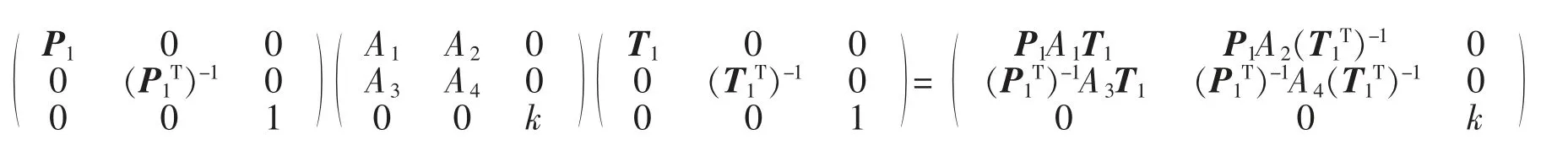
由于 B3的秩为 1,可设从而有
综上可得GA=G5G4G2G3G4G5G2。

