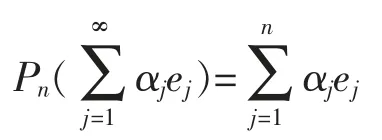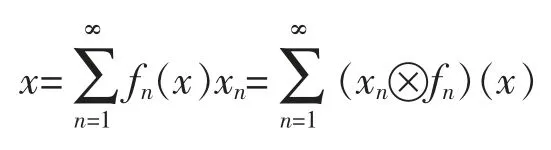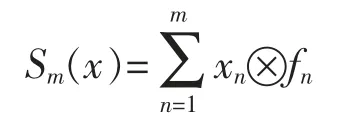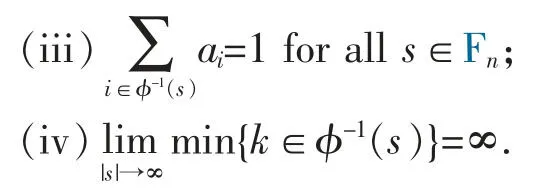Approximation properties and frames for Banach and operator spaces
HU Qianfeng,LIU Rui
(School of Mathematical Sciences,Nankai University,Tianjin 300071,China;The Key Laboratory of Pure Mathematics and Combinatorics,Ministry of Education,Tianjin 300071,China)
Abstract: We have made a survey of the main results on approximation properties and frames for Banach spaces and operator spaces.By introducing Schauder frame and completely bounded frame,we have presented the equivalent characterizations of the bounded approximation properties for Banach spaces and the completely bounded approximation properties for operator spaces.We have also provided some examples and the duality theory on complemented embedding,and introduced some open questions.
Key words: approximation property;Banach space;completely bounded frame;operator space;Schauder frame
1 Frames for Hilbert spaces
In 1952,Frames in Hilbert spaces were introduced by Duffin and Schaeffer[1].The current popularity of various concrete frames is largely due to their successful application to applied fields,such as signal processing,initiated by Daubechies,Grossmann,and Meyer in 1986[2].The motivation came from applications to signal analysis,as well as from applications to a wide variety of areas of mathematics,such as,sampling theory[3],operator algebra and group representation[4],harmonic analysis[5],nonlinear sparse approximation[6],and quantum computing[7].Recently,the theory of frames also showed essential connections to completely solve the Kadison-Singer Problem[8-9].
A frame for a Hilbert space H is a sequence of vectorsand there are constants 0 The equality in (2) allows the reconstruction formula of any vector x in the Hilbert space from the sequence of coefficientsThe canonical method to construct a dual frameis to take fi=S-1xifor all i∈N,where S is an invertible and positive operator on H with respect todefined byfor all x∈H.The operator S is called the frame operator of,and the dual frameis called the canonical dual frame of. In 1988,Feichtinger and Gröchenig[10]extended the classical concept of frames to Banach spaces by introducing atomic decompositions (and more generally,Banach frame,in [11]).The main goal of Ref [11]was to give the unique association of an element in a Banach space with the natural set of redundant frame coefficients. Definition 1[12]For a Banach space X,let Xdbe an associated Banach space of scalar valued sequences indexed by N.The sequencesis said to be an atomic decomposition of X with respect to Xdprovided for (a) fj(x)∈Xd,for each x∈X, (b)there exist constants A,B>0 such that In 2008,Schauder frames for Banach space were developed[13]to create a procedure to represent vectors using quantized coefficients.A Schauder frame essentially takes,as its definition,an extension of the dual expansion formula (2) from Hilbert space to Banach spaces.Moreover,a separable Banach space has a Schauder frame if and only if it has the Bounded Approximation Property[13-14].Suppose X is separable.If X has the Bounded Approximation Property(BAP),then this net can be replaced by a sequence Tn;alternatively,X has the BAP if there is a sequence of finite-rank maps Fn:X→X such that Recall that A separable Banach space has the BAP if and only if it is isomorphic to a complemented subspace of a Banach space with a Schauder basis[15-16].In the rest of the paper,we will employ the Schauder frame introduced by Casazza,Han and Larson[4,14].First of all,we introduce the concept of Schauder frames for Banach spaces,which is a natural generalization of frames for Hilbert spaces and Schauder bases for Banach spaces. Definition 2A separable Banach space X has a (Schauder) frame if there is a sequence (xj,fj)⊂X×X*such that In this case,we call (xj,fj) a (Schauder) frame for X. Theorem 1For a separable Banach space X,the following are equivalent: (i) X has the bounded approximation property; (ii) X has a Schauder frame; (iii) X is isomorphic to a complemented subspace of a Banach space with a Schauder basis. Thus,there are Banach spaces with Schauder frames which have no Schauder basis.In 2008,Casazza,Dilworth,Odell,Schlumprecht and Zsák considered Schauder frames and approximation problems in Banach spaces[13].Both Schauder frames and atomic decompositions are natural generalizations of redundant frame from Hilbert spaces to Banach spaces.These concepts are closely related,and some mentioned above in the area such as [14],[17],and [18]are stated in terms of atomic decompositions,while others such as [13],[19],and [20]are stated in terms of Schauder frames. Definition 3[12,21]For a Banach space X,let Xdbe an associated Banach space of scalar valued sequences indexed by N.The sequencesis said to be an atomic decomposition of X with respect to Xdprovided for (a) fj(x)∈Xd,for each x∈X, (b)there exist constants A,B>0 such that In 2009,D.Carando and S.Lassalle consider the duality theory for Schauder frames (atomic decomposition)[17]. Definition 4Given a Schauder frame (xi,fi)⊂X×X*,let Tn:X→X be the operatorThe frame (xi,fi) is called shrinking if ||x*◦Tn||→0 for all x*∈X*.The frame (xi,fi) is called boundedly complete ifconverges in norm to an element of X for all x**∈X**. In [19],Liu introduced the concepts of minimal and maximal associated bases with respect to Schauder frames,closely connected them to the duality theory,and extended well-known James’ theorem[19]on unconditional bases to unconditional frames. Theorem 2[19]Let (xi,fi)⊂X×X*be a Schauder frame of a Banach space X and assume that for all m∈NThen the following are equivalent. (a) (xi,fi) is shrinking. (b) Every normalized block of (xi) is weakly null. (d)The minimal associated basis is shrinking. Theorem 3[19]Let (xi,fi)⊂X×X*be a unconditional Schauder frame of a Banach space X and assume that for all m∈N Then X is reflexive if an only if X does not contain isomorphic copies of c0and l1. In 2011,Carando,Lassalle and Schmidberg[18]proved the above result without the local condition.In [20],Liu and Zheng gave an characterization of Schauder frames which are near-Schauder bases,which extended Holub's results[18]from Hilbert frames to Schauder frames. Definition 5[20]Let X be a Banach space with (xi)⊂X.We call (xi) a near-Schauder basis of X if there is a finite set σ⊂N such that (xi)i∉σis a Schauder basis of X.We call a Schauder frame (xi,fi) a near-Schauder basis if (xi) is a near-Schauder basis. We define the excess of a near-Schauder basis (xi) of X by Theorem 4[20]Let (xi,fi) be a Schauder frame of a Banach space X and let (Emin,()) be the minimalassociated sequence space to (xi,fi) with Sminthe minimal-associated recon-struction operator.Then the following conditions are equivalent: (a) The kernel of Smincontains no copy of c0; (b) Sminhas a finite dimensional kernel; (c) (xi) is a near-Schauder basis of X.Furthermore,in this case,we have In 2015,Beanland,Freeman and the author proved that the upper and lower estimate theorems for finite dimensional decompositions of Banach spaces can be extended to Schauder frames,and gave a complete characterization on duality theorem for Schauder frames. Theorem 5[21]Let (xi,fi) be a Schauder frame for a Banach space X.Then (xi,fi) is shrinking if and only if (xi,fi) has a shrinking associated basis.Furthermore,(xi,fi) is shrinking and boundedly complete if and only if(xi,fi) has a reflexive associated space. However it’s still open for unconditional (Schauder) frames and bases,which is fundamental for duality dilation problem of operator-valued measures on Banach spaces[22]. Now we turn to the approximation property of operator space.Let A be an operator space[23-25].We use Mnto denote the set of all n×n complex matrices,and Mn(A) to denote the set of all n×n matrices with entries from A.Given two operator spaces A and B and a map φ : A→B,obtain maps φn: Mn(A)→Mn(B) via the formula φn((ai,j))=(φ(ai,j)).The map φ is called completely bounded if φ is bounded and ||φ||cb=supn||φn|| is finite. In 2004,Junge,Nielsen,Ruan and Xu[26]extended the results of Johnson,Rosenthal and Zippin[15]on bases from Banach spaces to operator spaces. Definition 6We say that an operator space X has a completely bounded basis (in short cb-basis) if X has a Schauder basis (ej) and the natural initial sum projections satisfy supn||Pn||cb<∞.In this case,we call (ej) a cb-basis of X. In particular,they proved that in Ref [26]: (i)every separable nuclear C*-algebra has a cb-basis; (ii) for 1 Let Fnbe the free group of two generators and let λ be the left regular representation of Fn.The reduced group C*-algebra(Fn) is defined to be the norm-closure of span{λs|s∈Fn} in B(l2(Fn)).We note that the existence of a Schauder basis for the noncommutative L1space L1(VN(Fn)) over the free group von Neumann algebra VN(Fn) or the reduced free group C*-algebra(Fn) is still an open problem. Motivated by these results,we can consider cb-frames for operator spaces.Here is the definition introduced in [28].Let X be an operator space and X*be its canonical operator dual.A sequence (xn,fn)⊂X×X*is a cbframe for X if (xn,fn) is a frame,i.e. for all x∈X,and the initial sums define completely bounded maps on X with supm||Sm||cb<∞. Proposition 1[28]There exists a cb-frame (xi,fi) of(Fn),which is an infinite convex decomposition of(λs⊗δs)s∈Fn,such that there is a surjective map φ :N→Fnand a sequence of positive scalars (ai) satisfying that: (i) xi=λφ(i),fi=aiδφ(i)for all i∈N; (ii) φ-1(s)⊂N is infinite for each s∈Fn; It is clear from the definition that if a separable operator space X has a cb-basis,then it must have the completely bounded approximation property (CBAP),i.e.there exists a sequence of finite-rank maps Sm:X→X such that supm supm||Sm||cb<∞ and Sm(x)→x for every x∈X. Theorem 6[28]Let X be a separable operator space.The following are equivalent: (i)X has the CBAP; (ii) X has a cb-frame; (iii) X is completely isomorphic to a completely complemented subspace of an operator space with a cb-basis. In particular,combing with an important result of Haagerup and Kraus[30],the reduced group C*-algebra(Γ) of a weakly amenable group Γ has a cb-frame. In 2004,Oikhberg and Ricard constructed a separable operator space X0which is isometric to l2,and such that every infinite-dimensional closed subspace of X0fails the completely bounded approximation property[31].Thus (by Gilles Pisier’s Perturbation Lemma[23]) we have Theorem 7[28]The Oikhberg-Ricard space X0can not be completely isomorphic to any subspace of an operator space with a cb-basis (or with a cb-frame). Notice that we give a characterization of an operator space which is completely isomorphic to a completely complemented subspace of an operator space with a cb-basis.Then we ask the following natural question:“What is the local characterization of a separable operator space which can be a subspace of an operator space with a cb-basis?” Proposition 2[28]Let X be a separable operator space.Then following are equivalent: (i)X is completely isomorphic to a subspace of an operator space with a cb-basis; (ii) X is completely isomorphic to a subspace of an operator space with a cb-frame; (iii) X is completely isomorphic to a subspace of a (not necessarily separable) operator space with the CBAP.

2 Schauder frames for Banach spaces

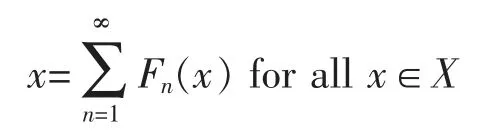
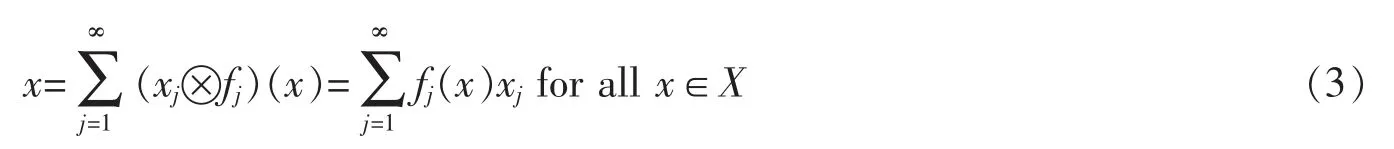

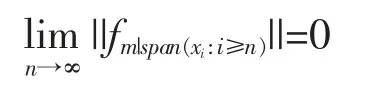
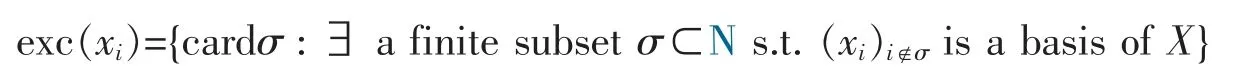
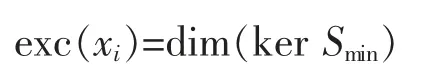
3 Completely bouneded frames for operator spaces