基于ESO的PMSLM无差拍电流预测控制

林 健，刘 晗，万 其，施昕昕，王通通，谢高硕

(南京工程学院 先进数控技术江苏省高校重点建设实验室，南京211100)

0 引 言

在PMSLM驱动系统中，电流环作为内环，其动态及稳态控制性能直接决定了直线电机推力的品质，因此高性能的电流控制策略受到了众多学者的关注[1]。对于PMSLM数字控制系统，采用无差拍电流预测控制可以以较少的计算量获得较好的跟踪性能，适合数字式控制[2-4]。该方法基于电机电压方程离散化模型来预测电压基准，通过SVPWM将其转化为相应的开关信号[5]。然而，无差拍预测控制完全依赖于精确的PMSLM模型，这意味着模型参数失配会使得计算的电压基准偏离其期望值。

为解决参数扰动问题，在文献[6]中，提出了一种采用增量调制器作为电流调节器的方法，可以有效地减小电流的稳态误差。在文献[7]中，设计了鲁棒预测电流控制方法，以减小电感参数失配引起的期望电流与测量电流之间的电流误差，但该方法忽略了永磁体磁链和电阻失配的影响。在文献[8]中，提出了用并联积分环方法进行预测控制，以补偿电机模型的不精确性和电机参数的变化，然而很难调整积分增益以获得较好的瞬态响应且不超调。

本文提出了一种改进的ESO，从电流量误差中提取扰动量的误差值，并将其用于观测扰动量，收敛速度快，同时利用时变增益的方式避免了初始时刻电流峰值过大。最后将改进的ESO用于观测扰动量，并应用于无差拍电流预测控制，提高了系统的鲁棒性。

1 ESO的设计

为了方便研究主要问题，将复杂的PMSLM系统简化，忽略电机绕组和永磁体的阻尼作用，忽略涡流和磁滞损耗，假设励磁磁场与电枢反应磁场均是正弦分布。在dq坐标系下的永磁同步直线电机数学模型可以表示为:

(1)

式中,R为初级电阻，为次级极距，φf为次级永磁体磁链，Ld、Lq分别为d、q轴电感分量，由于采用的是表贴式结构，因此可以Ld=Lq=L。ud、uq分别为初级d、q轴电压，id、iq分别为初级d、q轴电流，v为初级运动速度。

电机参数受系统工况等不确定因素影响，实际参数与标称参数会有偏差，式(1)变为

(2)

式中,R0、L0、φf0为电机电阻、电感、磁链的标称参数。ΔR、ΔL、Δφf为电机电阻、电感、磁链的参数偏差，ΔR=R-R0，ΔL=L-L0，Δφf=φf-φf0

若令ESO中电压ud、uq作为输入量，电流id、iq作为状态量，其余量分别作为dq轴总扰动fd、fq：

(3)

(4)

(5)

可以看出，传统ESO通过电流量的观测值和实际值的误差e1，来调节观测值的导数。用e1调节电流的导数符合误差控制原理，但若是用于调节扰动观测值z2的导数，将导致收敛速度变慢[9-11]。为此考虑将扰动量误差e2也加以利用，并用以调节z2的导数。由于扰动量无法直接测量，考虑从式(4)和式(5)中，通过用z1的导数和x1的导数相减来提取：

(6)

(7)

然而式(7)所示的ESO依然是高增益观测器，这将导致系统初始时刻出现峰值过大现象，甚至引发震荡问题[12]。本文将观测器的增益设计为时变增益，在初始时刻设置较小的增益来抑制峰值过大问题，随后逐渐增大并稳定于一个常值。设定增益为比例函数：

(8)

式中,γi和ηi为常数，ki为比例系数，ti为时间，i=1,2。

2 观测器稳定性分析

无差拍预测控制是一种离散化的控制系统，因此观测器的稳定性分析要基于离散化模型，将状态空间描述和改进后的ESO进行前向欧拉离散化，可得：

x(k+1)=A1x(k)+B1u(k)+E1h(k)

(9)

z(k+1)=A1z(k)+B1u(k)-L2(k)e(k)

(10)

式(9)和式(10)中，状态转移矩阵变为A1=TA+I；控制矩阵变为B1=TB；干扰矩阵变为E1=TE；观测器增益矩阵变为L2=TL1；T为采样周期；I为单位矩阵。

假设采样周期T足够小，扰动在两个采样周期内几乎不变，则h(k)可以忽略。将式(9)和式(10)相减，可得误差状态矩阵：

(11)

由于e2(k)中含有e1(k+1)，考虑通过线性变换分析误差状态：

(12)

则观测器的特征方程为

(13)

因为ESO增益均大于0，可知观测器所有特征根均为负实部，即观测器极点均分布于z域单位圆内，观测器稳定[13]。离散ESO结构如图1所示。

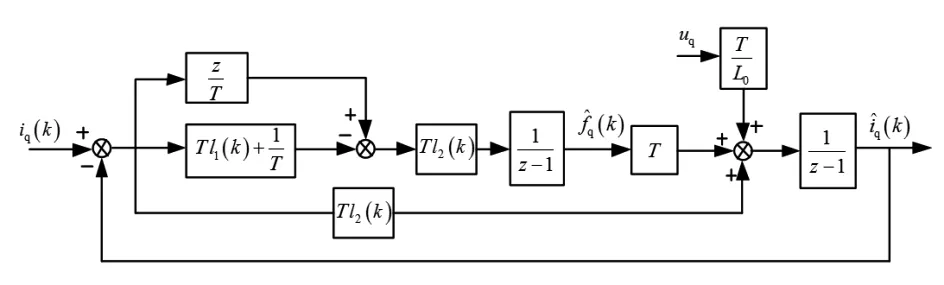
图1 离散ESO结构图

3 基于ESO的无差拍电流预测控制

将上述ESO观测出的dq轴系统扰动，引入至电压方程式(3)中，并将之离散化，得到基于ESO的电流预测控制算法：

(14)

图2 基于ESO的电流预测控制算法框图

4 实验结果

本文采用的实验平台如图3所示，其中PMSLM由Kollmorgen公司生产，电机的参数如下：电感L=0.0134 H，电阻R=1.3 Ω，极距=0.032 m，磁链ψ=0.11 Wb，阻尼系数为0.2 Ns/m，采样周期为T=100 μs。平台的配套软件系统可以对直线伺服系统的运行方式进行监控、设置，实时读取实验数据并保存，用于后续的分析与处理。

图3 直线电机伺服实验平台

为了验证设计的电流预测控制算法有效性，分别利用传统ESO和改进ESO，进行了电机电流跟踪和速度跟踪试验。首先，分别将控制器中的电感、磁链、电阻的给定参数设定为2.5L、0.5ψ、0.2R，采用id=0的控制策略并给定电流iq=2A。改进ESO参数为：γ1=3，η1=6，t1=4 ms，γ2=400，η2=600，t2=4 ms。传统ESO参数为：l1=4，l2=600。结果如图4～图6所示，当电感给定值为2.5L，无ESO的无差拍预测控制系统的谐波含量逐渐增大，将会失稳，并且电流响应速度较慢；当磁链给定值为0.5ψ，无ESO的系统，iq存在偏差且偏差逐渐增大；当电阻给定值为0.2R时，iq存在恒定偏差；而应用传统ESO和改进ESO的控制方法，都可以抑制参数扰动带来的问题，但是改进ESO更好的抑制了峰值，且电流跟踪速度更快。

比较速度跟踪性能时，令给定电机速度为100 mm/s，外加负载力为300 N，将控制器中电感、磁链、电阻等参数给定值设为2.5L、0.5ψ、0.2R，图7为对应的速度跟踪波形比较，应用改进ESO的无差拍预测控制，启动时电机速度波动更小，启动后速度更加平稳，而传统ESO补偿下的无差拍预测控制，在初始时刻峰值较高且出现了震荡。实验结果表明，本文提出的电流控制算法初始时刻峰值较低，响应速度快，避免了参数扰动造成的电流静差以及失稳问题。

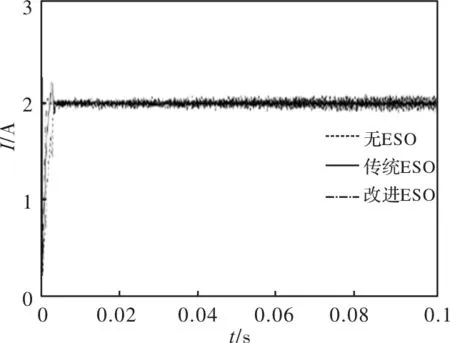
图4 给定电感2.5L时电流跟踪波形比较

图5 给定磁链0.5ψ时电流跟踪波形比较

图6 给定电阻0.2R时电流跟踪波形比较

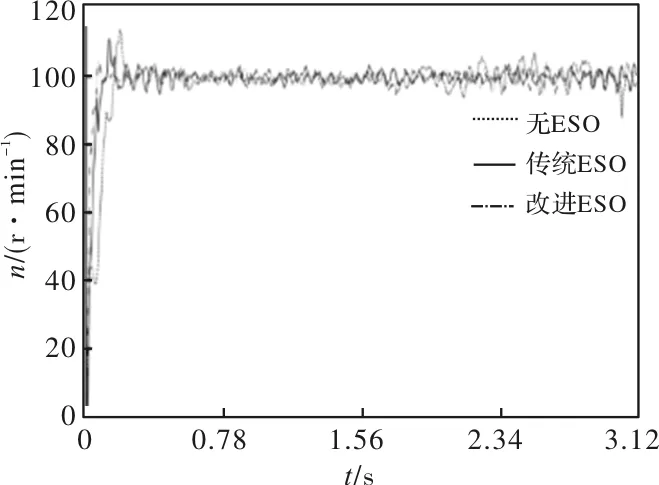
图7 存在差数偏差时速度波形跟踪比较

5 结 语

为解决PMSLM无差拍预测控制系统中参数扰动带来的电流静差及失稳等问题，将参数扰动引入电压方程并建立数学模型。并在此基础上提出了一种改进ESO。从电流量误差中提取扰动量误差的信息，根据误差控制原理，将其用来调节扰动量观测值，加快了观测器的跟踪速度，并且设计了时变的增益用以抑制电流峰值过大问题。从数学上证明了该观测器的稳定性，并将其用于无差拍控制系统的电流实时补偿。最后在PMSLM控制系统试验平台上，给定电流和速度下，开展系统不同参数存在偏差时的电流与速度跟踪试验，结果表明该方法对系统参数偏差带来的扰动具有较强的鲁棒性，有更快的电流跟踪速度且有效抑制了初始时刻电流峰值。