基于LMI的永磁同步伺服电机的混合H2/H∞鲁棒预测控制器

王凯东，李宏浩

(沈阳工业大学 国家稀土永磁电机工程技术研究中心，沈阳 110870)

0 引 言

永磁同步电机具有结构简单、运行可靠，高效率等特点，在牵引系统、高精密控制系统等场合广泛应用，特别是在高精度数控机床。采用永磁同步电机直接驱动的伺服系统中，不需要经过机械传动结构，负载与永磁同步电机直接相连。但采用这种直接连接的方式也带来许多问题，如负载扰动、参数变化等，这对所设计的控制器能否保证系统的稳定性和抗干扰性能提出了更高的要求。因此，高精度永磁同步伺服电机系统必须满足低速重切削、高速重加工以及负载突然变化系统的稳定性、快速性，也就是要求系统具有一定的鲁棒性。在实际应用中,不可避免地存在外界扰动以及系统不确定性, 而模型预测控制由于能够方便地处理各种约束。因此,鲁棒预测控制作为模型预测控制的重要分支,近年来受到各界的广泛关注[1-2]。

由于可以方便地描述非线性对象以及参数变化对象等,不确定系统的预测控制器设计获得普遍应用[3-6]。文献基于不变集理论,采用LMI方法设计了鲁棒控制器，考虑了H∞指标下的有约束预测控制问题。

文献[4]考虑了H∞指标下的有约束预测控制问题.文献[6]通过离线设计两个椭圆不变集以降低设计的保守性,进而提出一种有界扰动系统的高效鲁棒预测控制器(SD-ERPC)的设计方法。文献[7]基于微分几何理论，把系统模型转化为线性模型而设计的H∞鲁棒控制器。

在实际应用中,人们通常可以选取H2性能指标来设计鲁棒控制器以获得较好的闭环控制性能。但是,外界扰动也是必须设计考虑的因素,否则可能会对整个闭环系统性能和稳定性造成潜在的威胁。因此,对于实际应用而言,如何在控制器的设计中有效地平衡H2和H∞性能指标是一个重要问题。因此,在鲁棒控制领域,一些研究者很自然的想到将二者结合。文献[8]针对有扰动的线性定常系统采用混合指标方法进行鲁棒预测控制器设计, 并将其应用到悬挂系统的控制中。文献[9]的设计将给定的H2性能指标作为前提条件,通过在线优化H2性能指标来决定系统的当前控制量,可以起到平衡系统的鲁棒性和闭环控制性能的作用。但是,由于文献[10]仍然采用文献[4]中的反馈律和Lyapunov函数的设计,其设计的保守性将导致系统较小可行域和较差的闭环控制性能。

因此，本文提出了一种基于LMI的混合H2/H∞的永磁同步伺服系统的鲁棒预测控制器，该控制器针永磁同步电机伺服系统,将混合的H2/H∞性能指标与模型预测控制方法相结合,并且使用LMI进行求解，使得系统具有较好的鲁棒性能和稳定性,同时具有良好的跟踪性能和较强的抗干扰能力。

1 永磁同步电机数学模型

永磁同步电机的在d-q坐标下的动态方程

(1)

永磁同步伺服电机是一个非线性、强耦合系统,并且为隐极式永磁同步电机，即Ld=Lq,采用id=0的控制策略，则永磁同步电机的电磁转矩方程可以简化为

(2)

运动方程

(3)

利用向前差分对状态方程离散化,得到以下离散化模型：

(4)

(5)

其中，s(k)=[id,iq,ωiq,ω]；u(k)=[ud,uq]；ω(k)=[0,0,0,TL]。式中，ud、uq、id、iq、Ld、Lq分别为d、q轴上的定子电压、电流和电感；Rs为定子相绕组电阻；ψf为永磁磁链；ω为转子角速度；J为转动惯量；B为粘滞摩擦系数；Te为电磁转矩；TL为负载转矩；np为极对数；t为时间步长。

2 基于LMI的混合H2/H∞鲁棒预测控制器的设计

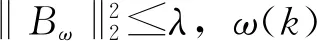
(1)H∞性能指标,即扰动ω(k)到系统输出z(k)的传递函数Tzω满足

‖Tzω‖∞≤γ

(6)

(2)H2性能指标,即系统输出z(k)满足

(7)

基于上述设计目标，一般事先给定其中的一个性能指标，优化另一个指标来设计控制器。文献[8]通过扩展文献[3]的方法给出了针对线性定常系统的混合H2/H∞鲁棒预测控制的方法,并未考虑系统的不确定性。对于文献[9]的方法由于扰动的存在无法保证系统的递归可行性。鉴于以上问题,本文提出了一种混合H2/H∞的鲁棒预测控制综计方法。

对控制策略中的反馈控制律u(k)=kx(k),设计Lyapunov函数V(x)=xTPx,且P>0。令φ(k)=A(k)+B(k)K，则

(8)

其中，

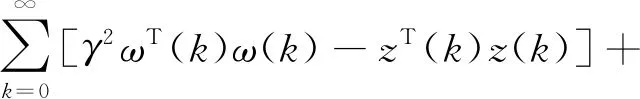
(9)

上式可转化

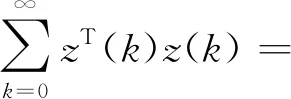
(10)

由式(10)可知：

(1)根据鲁棒控制理论,性能指标即扰动ω(k)到系统输出z(k)的传递函数Tzω满足‖Tzω‖∞≤γ；因此，当x(0)=0时扰动到输出的传递性能为

(11)

所以若式(10)中M(k)≤0成立,则式(11)得以满足,即H∞性能指标得以满足。

(2)当M(k)≤0时，若

(12)

满足,则H2性能指标得以满足。其中M(k)≤0可改写为

(13)

式(13)可以转化为

(14)

应用Schur补性质,式(13)可写成LMI形式

(15)

由式(14)可知,如果不确定系统模型的每个顶点都满足式(14),则其凸组合也必然满足式(14)。令Q=αP-1,K=YQ-1并将式(14)左、右乘以diag(P-1,I,I,I,I),可得若

(16)

满足，则式(14)可以满足。

考虑系统的不确定性时,式(16)即退化为文献[8]中的结论。综上所述,当系统满足式(15)和式(16)时,系统同时满足H2和H∞的性能指标。

3 系统可行性条件

考虑式(8),式(12)和式(15)可知,式(15)仅仅保证M(k)≤0。由式(8)可知,由于扰动存在,式(11)和式(12)不能保证γ2ωT(k)ω(k)-zT(k)z(k)<0始终成立。也就是说,当扰动存在时,不能保证Lyapunov函数递减。因此,即便M(k)≤0,V(x(k+1))-V(x(k))≤0不是始终成立。这也就意味着,即便当前状态x(k)属于集合{x|xTQ-1x≤1},下一时刻状态x(k+i)不能保证属于{x|xTQ-1x≤1}。文献[8]并没有注意到这个问题,因此其算法不能保证递归可行性。设当前系统状态为x(k), 则下一时刻系统状态为φ(k)x(k)+Bωω(k),令V(k)=Bωω(k),x(k+1)为名义系统状态,要使系统状态x(k+1)处于椭圆内,即要求xT(k+1)Q-1x(k+1)≤xT(k)Q-1x(k)≤1,等价于

(17)

[Bωω(k)ω(k)]T[Bωω(k)ω(k)]≤λωmaxI

式(18)可分解为

(18)

(19)

其中0≤α≤1，如果保证式(18)和式(19)成立，则式(17)成立，既保证了系统状态x(k+1)处于椭圆里面。α为给定量，并且式(19)等价于

(20)

由文献[10]，若

π=(1-α)(Q-λωmaxIα-1),i=1,2,…

(21)

成立，则是式(16)和式(19)成立。

如果系统当前状态x(k)满足式 (15), 则其处于集合{x|xTQ-1x≤1}中; 如果同时式 (18) 和式(19) 也满足, 则可保证x(k+1)仍处于该集合中。 因为(1-α)Q≥(1-α)(Q-ωmaxIα-1), 由式 (21) 可得, 较大的α会造成系统可行域减小。

类似文献[3]，对于集合{x|xTQ-1x≤1}，如果满足

(22)

可以满足，则约束条件式(4)可以保证，其中Zii为矩阵Z的对角线元素。对于约束条件(5)可以类似表示为

(23)

综上所述，当给定H∞性能指标γ，可以表示为

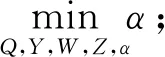
(24)

s.t.式(21)，式(22)，式(23)

式(24)中，式(21)保证了系统H2/H∞指标，式(22)、式(23)保证系统输出和输入的约束。通过LMI求解工具，解出预测控制器K。

对于控制器(24),给定H2指标α，反过来也可以类似地给定H∞指标γ为优化目标得到H∞鲁棒预测控制器。

定理1 对于系统(5),在k时刻，式(23)可行，则闭环系统稳定。

4 仿真及分析结果

为了验证混合H2/H∞鲁棒预测控制器有效性，采用Matlab/Simulink进行仿真研究。PMSM伺服系统的参数为:磁链ψf=0.812 Wb，定子电阻Rs=0.506Ω,电感0.6385mH。带入离散状态方程，得到状态方程参数分别为

根据式(22)，利用Matlab自带的LMI工具箱进行求解，求得的混合H2/H∞鲁棒预测控制器K为

图1、图2分别为采用PI调节器和鲁棒预测控制器K的闭环系统阶跃响应曲线，从图中可以看出永磁电机在空载下，采用鲁棒预测控制器K时的闭环系统的动态响应要比采用PI调节器快，超调量小，且不影响其稳定性，改善了永磁伺服电机的动态响应能力，满足其对快速性的要求。

由于永磁伺服电机系统易受负载扰动的影响。因此，当系统稳定时，负载转矩突然变大。采用混合H2/H∞鲁棒预测控制器K所得到的闭环系统阶跃响应曲线如图3所示。仿真结果表明，当负载转矩发生较大变化，所设计的控制器K仍能使闭环系统在较短时间内达到稳态，而且超调较小，这说明伺服系统对参数变化具有较强的鲁棒稳定性。

在t=0.3s时加扰动TL=2Te，混合H2/H∞鲁棒预测控制器闭环系统阶跃响应曲线如图4所示。仿真结果表明，在突加负载扰动情况下，闭环系统仍能短时间内恢复稳定，说明系统具有较强的抗干扰能力，满足了永磁电机伺服系统对抗干扰能力的要求。

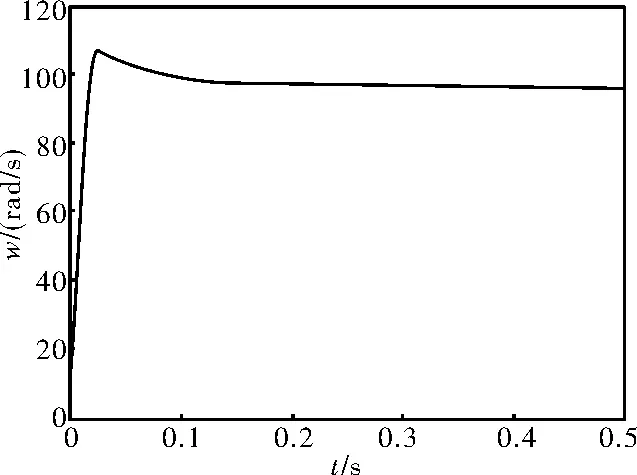
图1 闭环系统阶跃响应曲线(PI调节器)

图2 闭环系统阶跃响应曲线(鲁棒预测)

图3 闭环系统阶跃响应曲线(混合H2/H∞鲁棒)

图4 t=0.3s闭环系统阶跃响应曲线(混合H2/H∞鲁棒)

5 结 论

由于数控车床采用永磁电机直接驱动技术，因而易受外界及自身扰动的影响，这直接影响了系统的伺服性能。本文基于LMI设计的混合H2/H∞鲁棒预测控制器同时考虑两个重要的鲁棒性能指标，不但保证了系统的稳定性，改善了闭环系统的动态响应性能，还使系统具有较强的鲁棒性，在一定程度上解决了快速性和鲁棒性之间的矛盾，满足了高精度直接驱动永磁电机伺服系统对快速性和鲁棒性的要求。