基于永磁体优化PMSM力波与模态分析

王 伟，黄开胜，胡 弼，胡土雄

(广东工业大学，广州 510006)

0 引 言

随着塑料工业技术的迅速发展，塑料制品已广泛应用于日常及社会生活的方方面面[1]。对于塑料制品的主要成型设备注塑机，相比于传统类型，电动类型注塑机具有更多优势，同时由于国内塑料市场对产品质量和各大生产厂商对控制精度要求的提高以及伺服节能型注塑机的兴起，PMSM被越来越多地用作注塑机的驱动电机，逐渐取代异步电机。因此，注塑机用PMSM的设计与分析具有重要的社会价值和意义[2]。

由于PMSM定子电枢上开齿槽，永磁体磁极与齿槽的相互作用引起了电机内磁场的变化，从而导致了振动和噪声等问题[3]。针对PMSM的减振降噪，科研学者与工程技术人员进行了大量的研究与实践。文献[4]针对内置式永磁同步电动机，采用偏移定子齿顶的方法来降低定子齿受到的较大径向电磁力，最终达到减振效果。文献[5]针对分数槽永磁同步电机，通过注入补偿电流的方法，消除径向力谐波，从而减振降噪，但该方法不适用于整数槽电机。文献[6]针对变频器供电引起的永磁同步电动机电磁振动噪声，通过综合随机开关频率调制技术与死区补偿技术的优点，可以有效降低高中低频振动与噪声。文献[7]针对电磁力和磁致伸缩效应对永磁电机振动和噪声的影响，通过建立电磁-机械耦合数学模型，并应用有限元仿真分析了电机的振动形变与声场分布，为减振降噪提供了理论分析方法和依据。文献[8]针对车用永磁电机的电磁振动噪声特性，通过对径向电磁力波的解析分析和机械机构的模态分析，并进行了实验测量和数值分析，验证了分析结论与频谱特征的一致性。

本文以一款注塑机用48槽8极PMSM为研究对象，通过电磁振动与噪声产生机理的推导分析，基于转子谐波磁场对径向电磁力波的影响性，在不改变定子磁场的基础上，采用扫描法对永磁体磁极的极弧系数、厚度、偏心距进行优化。在达到降低气隙磁场谐波畸变率的效果后，综合多种因素优选数值，对优化前后的电机模型进行电磁力波与模态的有限元仿真，经过对比分析验证了该方法的有效性。

1 PMSM电磁振动与噪声产生机理

电磁振动噪声相对于机械与空气动力所产生的振动噪声，是电机的最主要噪声源。在PMSM运行时，气隙中存在径向电磁力波，其作用于定子铁心，引起定子径向振动发生形变，并由内往外传递，从而产生电磁噪声。

由定子磁场与转子磁场相互作用产生的径向电磁力波，是引起电磁振动噪声的主要因素，其次数越低、则形变就越大；同时定子铁心形变量随着力波幅值的增大而加剧，随着力波次数的四次方的增大而弱化，因此大幅值低次数的径向电磁力波是电磁振动噪声的主要根源。

根据麦克斯韦理论，可得到定子铁心内表面的径向电磁力波Pr(θ,t)为

(1)

式中,μ0为真空磁导率，b(θ,t)为气隙磁密。

当不考虑饱和效应与铁心磁阻的影响时，可得到气隙磁密b(θ,t)为

b(θ,t)=λ(θ,t)·f(θ,t)

(2)

式中,λ(θ,t)为气隙比磁导，f(θ,t)为气隙磁动势。

当考虑表贴式PMSM定子的齿槽时，可得到气隙比磁导λ(θ,t)为

λ(θ,t)=Λ0+∑λl1

(3)

式中,Λ0为单位面积气隙磁导的不变量，λl1为定子齿槽引起的谐波比磁导的周期量。

当三相绕组通入三相对称电流时，PMSM气隙磁动势由定子基波磁动势、定子谐波磁动势和转子永磁体谐波磁动势所组成，可得到气隙磁动势f(θ,t)为

(4)

式中,p为电机极对数，ω0为基频，ν为定子磁场谐波极对数，μ为永磁体磁场谐波极对数。

将式(3)、式(4)代入式(2)，并忽略掉谐波比磁导的周期量λl1；同时代入式(1)得：

(5)

由定子磁场和转子磁场相互作用时产生小于4次的一系列低次数、大幅值径向电磁力波是引起电机振动和噪声的主要根源。因此，忽略高次数、低幅值的径向电磁力波；同时只考虑对铁心形变及振动和噪声影响最大的部分。此时可得到径向电磁力波Pr(θ,t)为

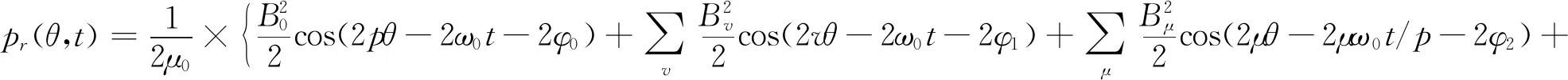
(6)

式中,定子基波和转子谐波相互作用产生的低次电磁力波，增大铁心形变量，进而加剧电磁振动和噪声。因此，针对转子永磁体磁场，着重研究该部分主要参数变化下所引起的径向电磁力波对电机振动和噪声的影响[10-11]。

2 永磁体磁极优化对气隙磁场的影响

通过电磁振动与噪声的解析分析，由定子基波和转子谐波磁场相互作用产生的低次力波是影响电机振动噪声较大的部分。因此，本文在不改变定子磁场的基础上，针对转子磁场采取扫描法优化永磁体磁极主要参数，分析极弧系数、磁极厚度以及磁极偏心距对气隙磁场的影响规律，以达到减小转子谐波含量，降低磁场谐波畸变率的目标，进而削弱径向电磁力波空间分布与时间分布的幅值，有效降低振动与噪声。

由式(1)可知，径向电磁力波与气隙磁密幅值的平方成正相关，所以，减小气隙磁场谐波含量，可以降低气隙磁密幅值，有效削弱径向电磁力波的幅值。通过Ansys有限元软件分别对极弧系数、磁极厚度、磁极偏心距定义参数，并设置参数的有效变量区间，在合理范围内进行参数扫描分析，得到不同参数变量对气隙磁场谐波畸变率的影响规律。

将极弧系数定义为参数a，取有效变量区间为0.6～0.95，以0.05为步长共8个变量。采用Ansys-Maxwell 2D对参数变量a进行扫描分析，可得到极弧系数参数变量扫描图以及对应的谐波畸变率折线图，如图1和图2所示。

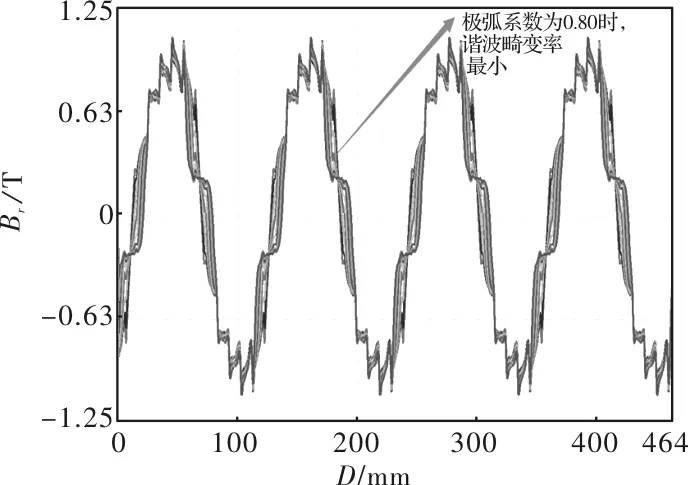
图1 极弧系数参数变量扫描图

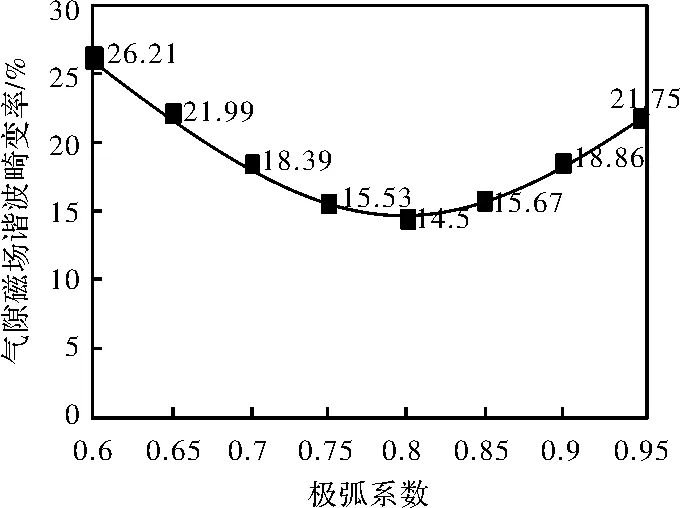
图2 不同极弧系数对应的谐波畸变率折线图

由图1可知，在8个变量取值中，当极弧系数取0.80时，气隙磁场谐波畸变率最小。

由图2可知，气隙磁场谐波畸变率随着极弧系数的增加，先是减小然后增大，呈凹状，在谷值a=0.80处取得最小谐波畸变率。

将磁极厚度定义为参数b，取有效变量区间为2～5.5，以0.5mm为步长共8个变量。采用Ansys-Maxwell 2D对参数变量b进行扫描分析，可得到磁极厚度参数变量扫描图以及对应的谐波畸变率折线图，如图3和图4所示。

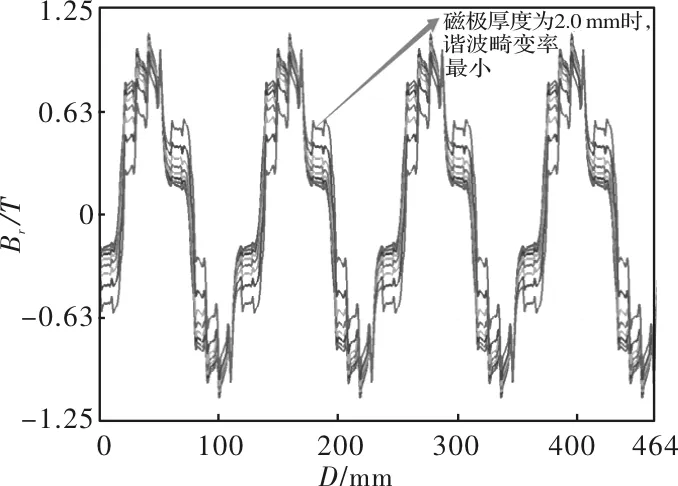
图3 磁极厚度参数变量扫描图

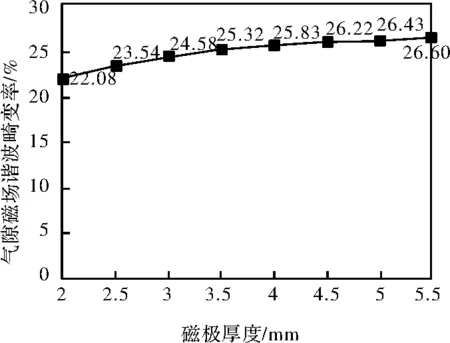
图4 不同磁极厚度对应的谐波畸变率折线图

由图3可知，在8个变量取值中，当磁极厚度取2.0mm时，气隙磁场谐波畸变率最小。

由图4可知，气隙磁场谐波畸变率随着磁极厚度的增加而增大，呈直线上升状，在始端b=2.0处取得最小谐波畸变率。

将磁极偏心距定义为参数c，取有效变量区间为16～30，以2mm为步长共8个变量。采用Ansys-Maxwell 2D对参数变量c进行扫描分析，可得到磁极偏心距参数变量扫描图以及对应的谐波畸变率折线图，如图5和图6所示。

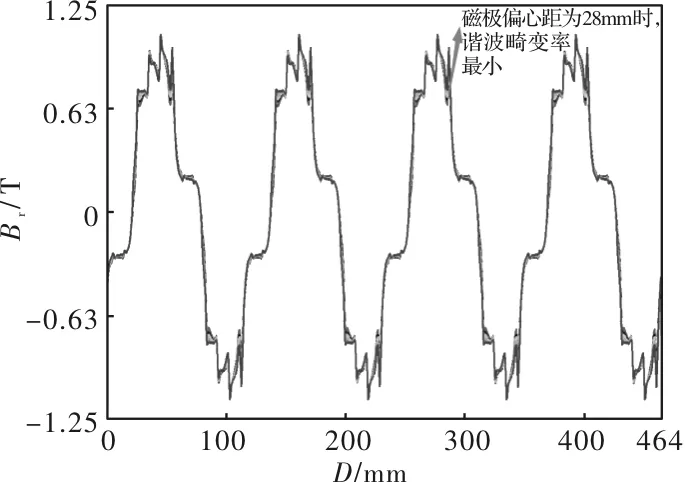
图5 磁极偏心距参数变量扫描图

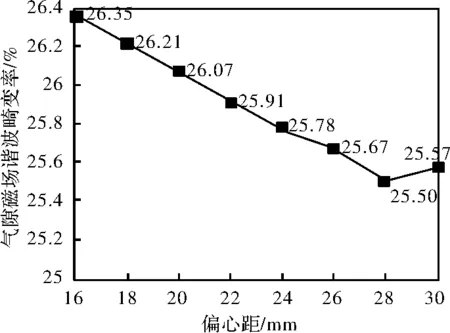
图6 不同磁极偏心距对应的谐波畸变率折线图

由图5可知，在8个变量取值中，当磁极偏心距取28mm时，气隙磁场谐波畸变率最小。

由图6可知，气隙磁场谐波畸变率随着磁极偏心距的增加，先是减小然后增大，呈凹状，在谷值c=28处取得最小谐波畸变率。

通过上述极弧系数、永磁体磁极厚度以及永磁体磁极偏心距的扫描分析，可看出三个参数分别在a=0.80，b=2.0，c=28时，各自对应的谐波畸变率最小。

但是，在实际工程中，通过优选极弧系数和磁极偏心距，可以使气隙磁密更加趋近于正弦性，降低气隙磁密的谐波畸变率。同时对于永磁体磁极厚度的选择亦是一个关键问题，磁极过厚会造成材料的浪费，提高成本；磁极过薄会造成加工的难度，且在温度、时间、外磁场、化学腐蚀、辐射、机械振动等极限工况下会造成不可逆退磁。因此，本文选取极弧系数为0.8，永磁体磁极厚度为3.5mm，永磁体磁极偏心距为26mm，以此参数变量建立电机模型，对其进行径向电磁力波空间分布与时间分布的仿真以及模态分析，探求优化后的转子永磁体磁场对电磁振动与噪声的影响效果。

3 PMSM电磁力波分析

通过Ansys-Maxwell 2D对永磁体磁极优化前后的电机进行建模，如图7所示。并对其进行空间与时间上的电磁力波仿真，分析其对力波次数和力波频率以及相应力波幅值的影响规律。

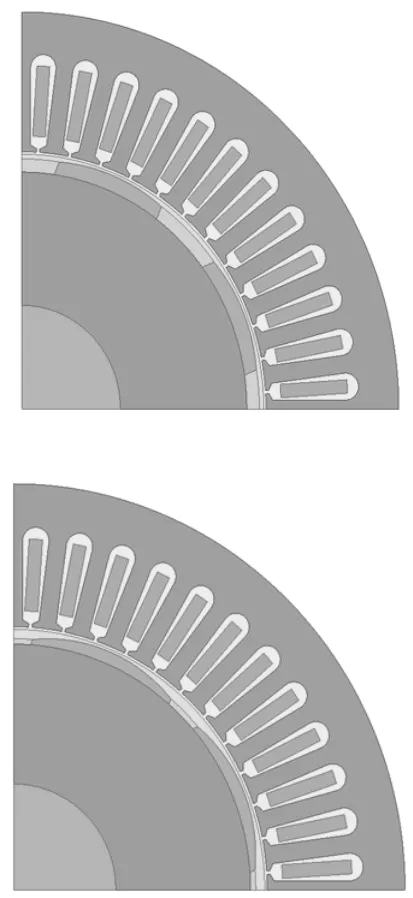
图7 永磁体优化前后Maxwell 2D 1/4电机模型

电磁力波次数：在额定运行时对径向电磁力波空间分布进行仿真，并绘制空间分布谐波分析图，如图8和图9所示。

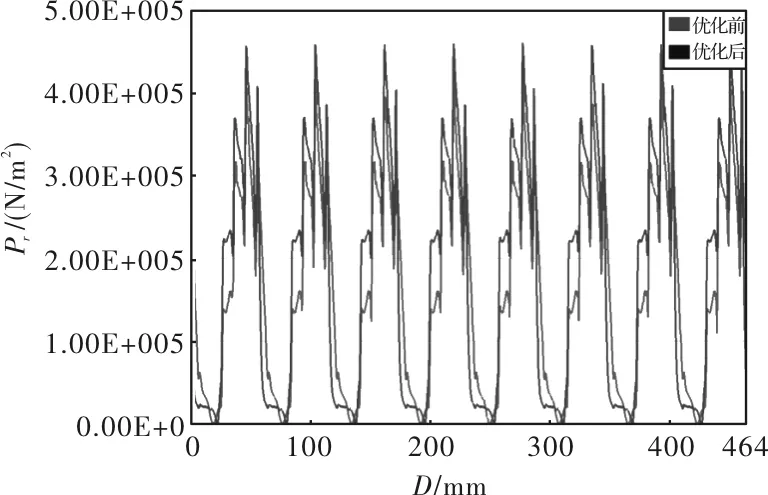
图8 永磁体优化前后径向电磁力波空间分布图

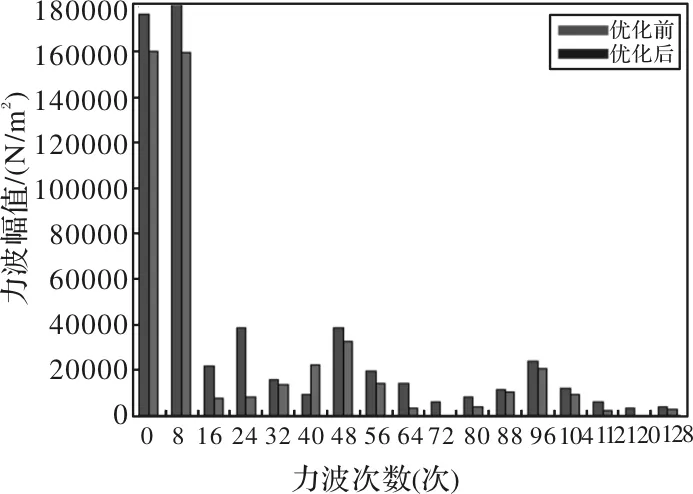
图9 永磁体优化前后径向电磁力波空间分布谐波分析图

由图8可知，优化后的径向电磁力波空间分布波形明显收敛，整体呈现在优化前的内部。由图9可知，优化后的径向电磁力波次数所对应的幅值整体呈下降趋势，除了在40次力波下，幅值有所增加，其余大幅度下降；同时，优化后的径向电磁力波消除了72次、120次力波。对于整数槽PMSM极对数大于2时影响电机振动和噪声的主要电磁力波次数为0次[12]，优化前其力波幅值为176.705kN/m2，优化后其力波幅值为160.170kN/m2，相比于优化前降低了9.4%。所以，通过优化永磁体磁极可以有效地降低电磁力波次数所对应的幅值，进而抑制电磁振动与噪声。

电磁力波频率：在额定运行时对径向电磁力波时间分布进行仿真，并绘制时间分布谐波分析图，如图10和图11所示。

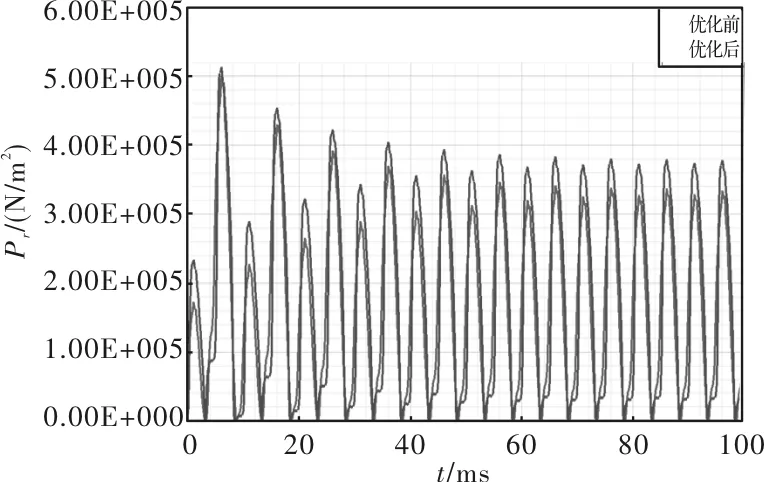
图10 永磁体优化前后径向电磁力波时间分布图

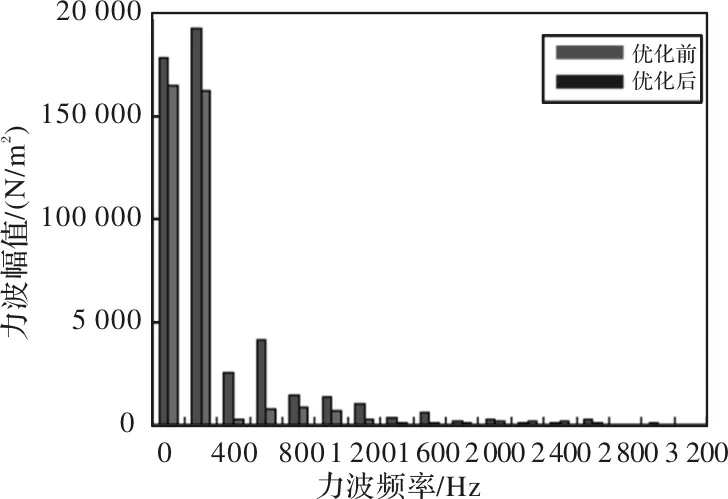
图11 永磁体优化前后径向电磁力波时间分布谐波分析图

由图10可知，优化后的径向电磁力波时间分布波形明显收敛，整体呈现在优化前的内部。由图11可知，优化后的径向电磁力波频率所对应的幅值整体呈下降趋势，除了个别高频所对应的幅值略微上升，其余大幅度下降；所以，通过优化永磁体磁极可以有效地降低电磁力波频率所对应的幅值，进而弱化与模态固有频率接近时所发生的共振现象。

综上所述，通过优化永磁体磁极，可以使径向电磁力波空间分与时间分布图对应的波形收敛，削弱了力波次数与力波幅值所对应的的幅值，同时不会影响力波本身的次数和频率，可以有效地抑制电磁振动与噪声。

4 PMSM模态分析

本文采用Ansys有限元软件对注塑机用PMSM进行模态分析，但由于电机外壳形状复杂，具有定位台阶、散热筋、螺丝等结构，故将电机外壳等效为圆环状柱体的理想状态，最终仿真得到整机结构各阶径向模态振型以及其所对应的固有频率[13]，如图12、图13和表1所示。

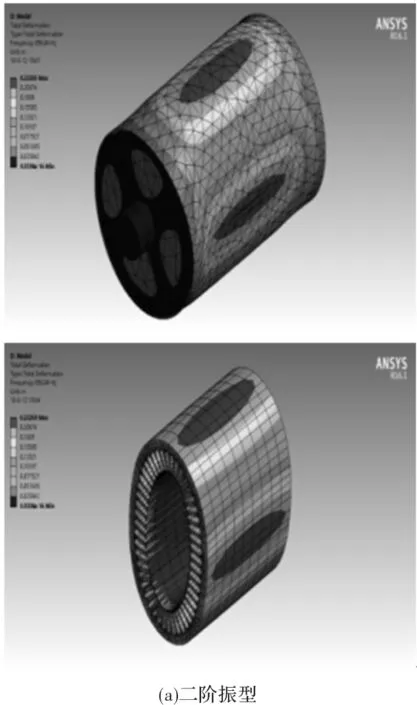
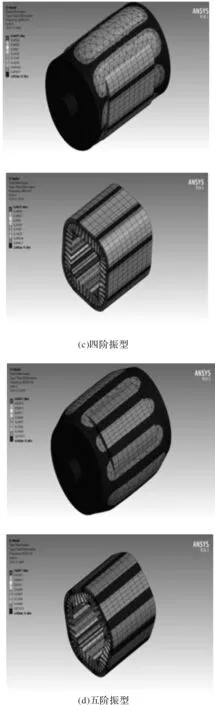
图12 永磁体磁极优化前PMSM整机2～5阶径向模态振型

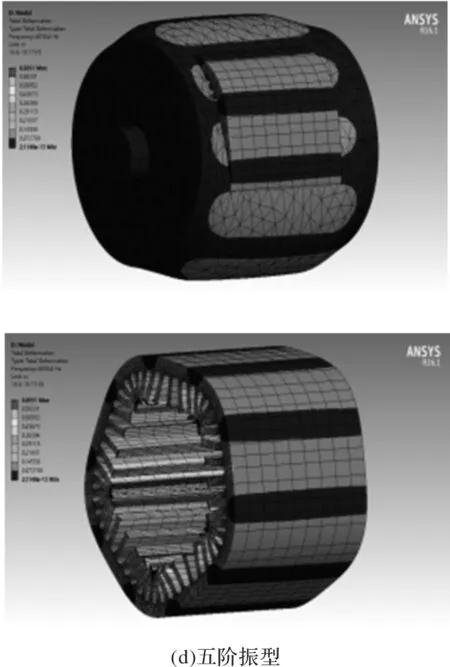
图13 永磁体磁极优化后PMSM整机2～5阶径向模态振型

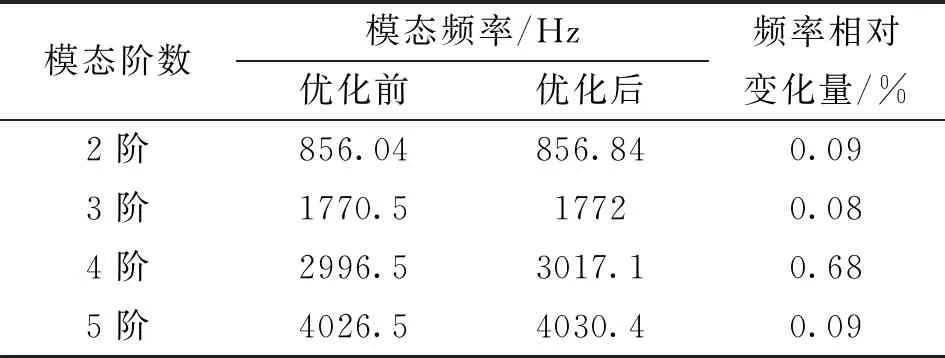
模态阶数模态频率/Hz优化前优化后频率相对变化量/%2阶856.04856.840.093阶1770.517720.084阶2996.53017.10.685阶4026.54030.40.09

注：由于篇幅限制，只节选部分低阶振型

由图12、图13可知，左侧视图为整机结构的2～5阶径向模态振型，右侧视图为在整机结构下定子铁心的2～5阶径向模态振型。通过图12与图13的各阶振型对比，可以看出各阶模态振型略有改变。

由表1可知，永磁体磁极优化前后整机结构的2～5阶径向模态固有频率发生轻微改变，相对变化量分别是2阶对应的0.09%、3阶对应的0.08%、4阶对应的0.68%、5阶对应的0.09%。根据刚度与质量效应及优化前后模态频率对比可知，优化后的永磁体磁极对整机结构的贡献为刚度不变、质量下降，所以提升了电机的固有频率。

为了避免共振现象，应当尽量规避电机固有频率与力波频率的接近。由表1和图11可知，对于2阶、3阶、4阶、5阶振型所对应的模态频率856.84Hz、1772Hz、3017.1Hz、4030.4Hz，高于径向电磁力波的自身频率800Hz、1600Hz、3000Hz、4000Hz。同时基于上述永磁体磁极的优化，将力波频率800Hz所对应的幅值由14.33kN/m2降到8.43kN/m2，降幅41.17%；力波频率1600Hz所对应的幅值由6.43kN/m2降到1.15kN/m2，降幅82.12%；力波频率3000Hz所对应的幅值由911.43N/m2降到184.69N/m2，降幅79.74%；力波频率4000Hz所对应的幅值由182.30N/m2降到169.37N/m2，降幅7.09%，而且其他频率所对应的幅值也大幅度下降。最终通过力波频率远离模态固有频率和大幅度削弱力波幅值，以达到减振降噪的效果。

5 结 语

本文简要解析分析电磁振动与噪声的产生机理，在不改变定子磁场的基础上，针对转子磁场，采用Ansys有限元软件对永磁体磁极的极弧系数、厚度、偏心距展开扫描分析，探究不同参数变量对气隙磁场谐波畸变率的影响规律，继而选择最佳参数变量，然后对优化前后的电磁力波与模态参数进行有限元仿真分析。结果表明，合理优化永磁体磁极，即在极弧系数为0.8，永磁体磁极厚度为3.5mm，永磁体磁极偏心距为26mm时，能有效削弱力波幅值，而且通过降低永磁体磁极质量，可以提升模态固有频率，使其高于径向电磁力波的自身频率，减少电磁共振的可能性。同时验证了该方法的可行性及普遍适用意义。