混合电动汽车用磁通切换型永磁电机冷却结构分析

陈 明,陆增洁

(1.国网上海市电力公司嘉定供电公司,上海 201899;2.国网上海市电力公司市北供电公司,上海 200072)

0 引 言

随着全球能源危机和环境污染的加剧，混合动力汽车(HEVs)由于其低能耗排量小而成为全球汽车市场和学者的关注焦点。起动发电机扮演着起动机和发电机的双重角色，因而是小型混合动力汽车的重要组成部分。小型混合动力汽车的重量和空间有限且对驱动电机的转矩、过载能力和效率要求较高，其起动发电机的转子通常直接与汽车引擎的调速轮耦合。磁通切换永磁电机因其高转矩密度、高功率密度和高效率在电动汽车、航天航空和船舶等行业有广泛的应用前景[1]。但是，磁通切换永磁电机电枢绕组的输入电流密度非常高(>20A/mm2)，远大于传统的大型发电机(>4A/mm2)，会导致电机温升过高。过高的温度会导致永磁体退磁和电机绝缘的老化，影响电机运行的安全稳定性，因而近年来磁通切换永磁电机的热分析引起了各国学者的广泛关注，是电机设计和制造时不可忽略的问题。

沈阳工业大学的唐任远等人考虑涡流反作用、开槽效应等因素，提出了可以计算任意定子电流波形的表面式无金属护套永磁同步电机的永磁体涡流损耗，并能分析任意次数时空谐波产生的永磁体涡流损耗[2]。东南大学的蔡秀花等人考虑了电机材料的各向异性、接触热阻以及对流散热等散热边界条件，在FEPG平台上开发了磁通切换永磁电机的损耗计算和温度场三维仿真的软件包，并且基于集总参数热模型计算电机各部件温升，验证FEPG平台软件包的计算结果[3]。沈阳工业大学的朱高嘉等人考虑损耗、材料导热系数、对流散热系数等受温度分布的影响,将温度场计算程序与一套双重循环迭代系统相嵌套，计算7k W盘式永磁电机的三维温度分布[4]。沈阳工业大学的佟文明等人基于流体力学和传热学理论，建立三维流固耦合共轭传热求解域模型，采用有限体积法进行流固耦合求解，得到转子有无轴向通风孔和通风孔与风刺相配合时电机内流体流动特性及各部件的温度分布，并研究通风孔尺寸、通风孔数量变化对流体场及温度场的影响[5]。美国学者Lindner A等人为定转子间气隙为3mm的低功率磁通切换永磁电机设计了2种冷却结构，发现通过在转子上挖斜槽来增加气隙内空气量，从而进一步提升定子内侧的冷却效果[6]。

本文以混合动力汽车的起动发电机，一台三相10kW的磁通切换永磁电机为研究对象，分析其损耗和温度场分布，并进行试验验证。首先基于时步有限元法计算电机损耗，并进行空载实验，验证损耗计算值的准确性。其次，在Ansys Fluent软件中分析了电机稳态温度场分布和暂态温度场分布，在混合动力平台上进行电机温升实验，验证温度场仿真的准确性。最后本文探究了冷却结构的对流散热系数和其几何参数间的数值关系，并通过计算流体力学仿真和电机水冷实验，优化电机冷却结构设计，提高冷却结构性能。

1 磁通切换型永磁电机损耗计算

本文所研究的磁通切换型永磁电机的主要设计参数如表1所示。

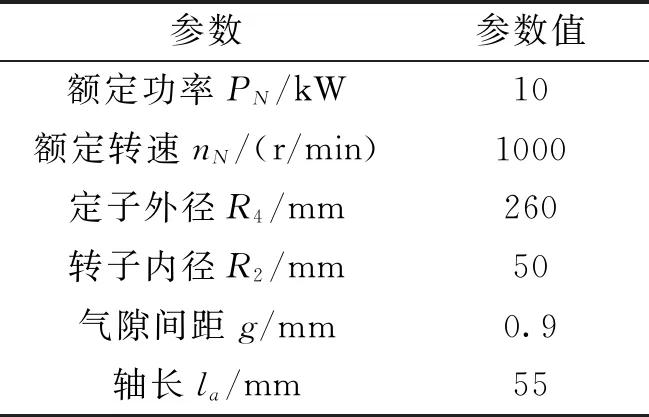
表1 磁通切换永磁电机的尺寸参数

磁通切换型永磁电机的损耗包括铁耗，永磁体和铝制机壳内的涡流损耗以及转轴摩擦损耗。依据意大利学者Bertotti G的经典铁耗计算模型[7]，铁耗包括经典涡流损耗、磁滞损耗和附加损耗，其计算公式如下：

(1)

式中，ph为磁滞损耗，W；pc为经典涡流损耗，W；pe为附加损耗，W；kh为磁滞损耗系数；kc为经典涡流损耗系数；ke为附加损耗系数；f为电机磁密变换频率，Hz；Bm为密幅值，T。

只有当电机磁密曲线为标准正弦波时，才能利用上式准确计算电机铁耗。本文所研究磁通切换电机关键点的磁密变化轨迹如图1所示，从图1(b)中可知电机的磁密变化曲线不是标准正弦波，而是含有大量小磁滞回环和直流偏置。为此本文将所得到的电机磁密进行正交化分解。

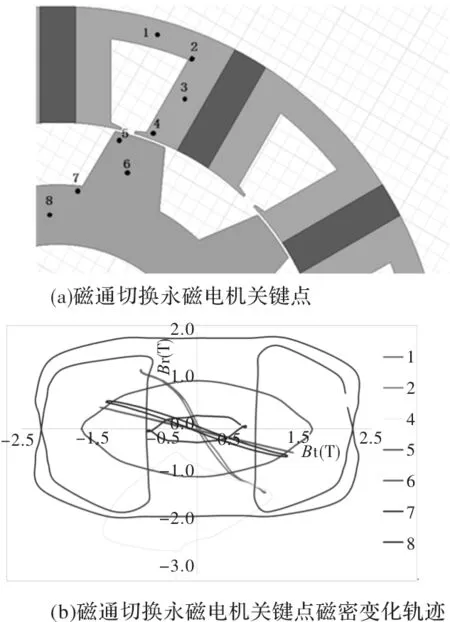
图1 磁通切换永磁电机关键点磁密变化轨迹

假设小磁滞回环与主磁滞回环形状相似，则电机磁密分可分为径向磁密和切向磁密，根据铁耗经典计算模型，利用时步有限元法，可以计算出考虑直流偏置的电机铁耗，其磁滞损耗[8]、经典涡流损耗[9]、附加损耗[10]以及总损耗的计算公式分别如下：

PFe=Ph+Pc+Pe

(2)

利用式(2)计算电机铁耗，结果如表2所示。

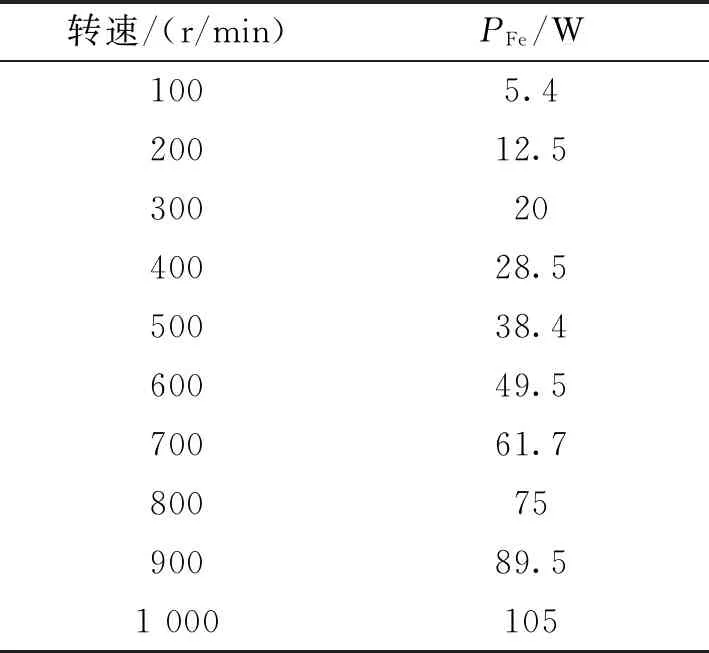
表2 不同转速下磁通切换永磁电机铁耗

本文采用有限元仿真软件得到电机永磁体的涡流损耗ppmc和铝制机壳的涡流损耗phc。不同转速下，电机永磁体的涡流损耗ppmc和铝制机壳的涡流损耗phc可以利用JMAG进行三维有限元仿真得到,如表3所示。

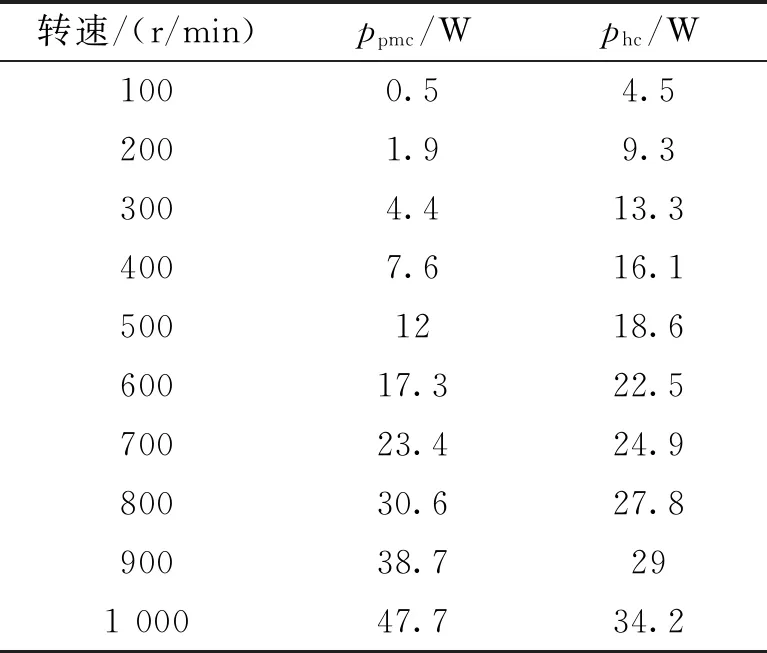
表3 不同转速下磁通切换永磁电机永磁体和铝壳空载涡流损耗

利用经验公式[11]可以计算得到电机的摩擦损耗：

(3)

式中，p为极对数；v为转子的周向速度，rad/s。

由于本文所研究的电机已经加工成型，难以通过实验测得电机铁耗，直接验证式(2)的正确性。故本文求取电机总损耗，通过实验测得总损耗，来验证式(2)的准确性。同一工况下，将其铁耗、永磁体的涡流损耗、铝壳的涡流损耗以及摩擦损耗求和得到电机的总损耗。

在混合动力平台上，利用DSP控制器驱动磁通切换永磁电机进行空载实验，电机拖动负载电机旋转，通过功率分析仪测量电机的输入功率。由于电机空载运行，故电机的输入功率近似等于电机的总损耗 。

式(2)考虑了直流偏置的影响，计算得到的总损耗接近实验值，验证了计算方法的准确性。

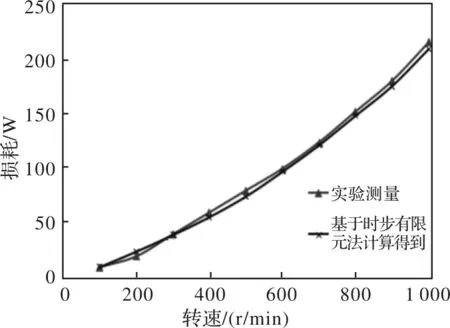
图2 电机的总损耗

2 永磁磁通切换电机中温升分布

在本文所研究的磁通切换永磁电机中，永磁体和绕组都嵌在定子上，铝制冷却机壳嵌套在定子外部，这样的安装方式有利于电机散热冷却。

图3 电机温升实验

基于上文计算的电机损耗，利用Ansys Fluent仿真电机温度场分布。当电机处于额定转速时，给电机电枢绕组中通入有效值为30.7A的相电流，利用Fluent仿真得到电机自然冷却条件下的暂态温度场分布，并在混合动力平台上进行温升实验，如图3所示，测得相同工况下电机温度的变化曲线，结果如图4所示。在相同工况下，给电机的冷却结构中通入流量为1800L/h的冷却水，利用Fluent仿真得到的电机各部件的温度变化曲线，在并在混合动力平台上进行温升实验测得电机温升曲线，如图5所示。图4和图5中虚线表示实验测得的电机各部件温度变化曲线，实线表示有限元法仿真得到的电机各部件温度变化曲线。

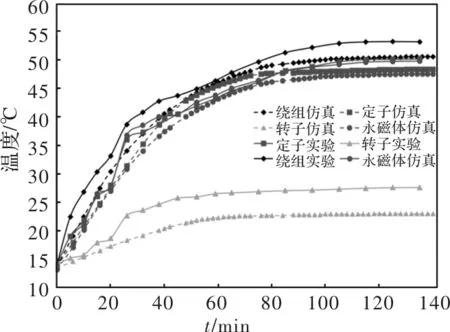
图4 实验和仿真得到的自然冷却条件下电机各部件的温度曲线

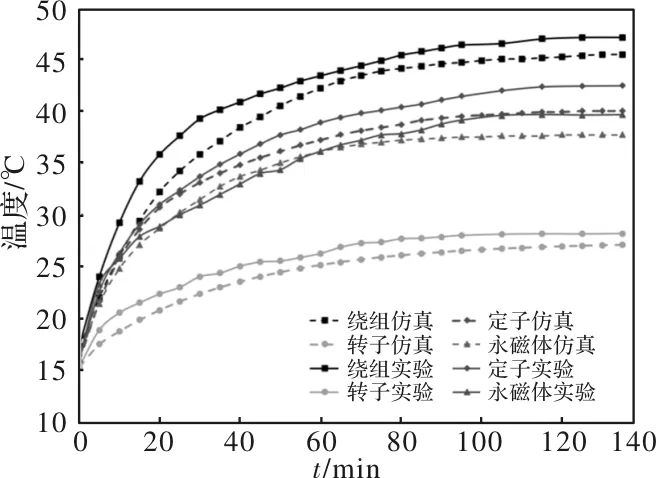
图5 实验和仿真得到的水冷条件下电机各部件的温度曲线

由图可知，电机的温度分布沿轴向变化大 。在自然冷却条件下，对比实验和有限元仿真得到的温度变化曲线，电机的最高温度均是在电枢绕组中，分别为50.1℃和52℃。在强迫水冷条件下，实验和有限元仿真得到的温度变化曲线中，电机的最高温度均依然是在电枢绕组中，分别为45.5 ℃和47.1 ℃。有限元仿真的误差均在合理范围内，说明了其准确性。

自然冷却条件下，定子铁心、绕组和永磁体三者的温度十分接近，但是在强迫水冷条件下定子铁心和永磁体的温度明显低于绕组温度，证明了冷却结构的有效性。

3 温度场数值分析模型的验证

3.1 水冷结构的散热系数

由于本文研究的磁通切换永磁电机电流密度大，电机温升较大，故需要用水冷结构冷却电机。根据水冷结构中不同的水流路径，可将水冷结构分为周向水冷结构、轴向水冷结构和并联水冷结构三种。周向水冷结构中，冷却水从入口进入冷却结构，沿着螺旋管道从出口流出；轴向水冷结构中冷却水沿着轴向流动，适用于轴长较长的大中型电机，并联型水冷结构中，水从入口进入后，沿着多个流道并行流至出口。本文研究的磁通切换永磁电机轴长只有55mm，不适用轴向水冷结构，因此下文主要探讨周向水冷结构和并联水冷结构。

在相同的入口横截面积和入口流量下，用Fluent仿真周向水冷结构和并联水冷结构的流体场分布，由有仿真结果可知，周向水冷结构的平均流速高于并联水冷结构的平均流速。因此本文研究的磁通切换永磁电机采用周向水冷结构。

本文研究的磁通切换永磁电机现有的水冷结构是流道数为1的周向水冷结构。

现有冷却结构中水的流动可近似为矩形流道中水的流动，从而求得其流体力学的无量纲常数。流体的普朗特常数计算公式如下:

(4)

式中，cf流体的比热容，J/(kg·K)；ηf为流体的动力粘度，N·s/m2；λf为流体的导热系数，W/(m·K)。

流体雷诺数的表达式如下：

(5)

式中，υ为流体的流速，m/s；vf为流体的动力粘度系数，m2/s；de为水力半径，m。

(6)

式中，A为流道的横截面积，m2；s为流道的湿周，m；b为流道的宽度，m；h为流道的高度，m。

由于现有水冷结构只有一个进出口和流道，故流道中流速的近似计算公式如下：

(7)

式中，Q为单位时间内流入水冷结构水的质量，kg/s。

在给定的水流流速下，计算得到雷诺数为4 203，因此冷却管道中的流体处于湍流状态，湍流的努塞尔常数可按如下公式[12]计算：

(8)

式中，ηw为冷却结构的动力粘度，N·s/m2。

由流体的相似准则可得[12]：

(9)

将式(5)、式(6)、式(7)和式(8)带入式(9)可得冷却结构的对流散热系数与其几何参数间的关系式：

(10)

由上式可知，当入口流量不变时，冷却结构流道的横截面积越小，其对流散热系数越大。然而过小的流道横截面难以加工，并会导致过大的入口流速，加速冷却结构的腐蚀，缩短冷却结构的使用寿命。

3.2 磁通切换永磁电机一维导热模型

一般而言，分析电机温度分布时，通常采用集总参数热模型和有限元法，但是这两种方法建模繁琐并且耗时长。因此，本节研究电机温度分布与水冷结构几何参数间的数值关系。由于本文所研究的磁通切换永磁电机结构对称，因而其温度分布也具有对称性。假设电机各个部件中的损耗均匀分布且将定子、永磁体和电枢绕组等效为一个各向同性的导热模块，其等效导热系数λavg计算公式如式(11)所示[13]，则电机导热模型可简化为圆柱坐标系下的一维稳态导热模型，如图6所示。

(11)

式中，As为定子的横截面积，m2；Asc为电枢绕组定子的横截面积，m2；Am为永磁体的横截面积，m2；λs为定子的导热系数，W/(m·K)；λsc为绕组的导热系数，W/(m·K)；λm为永磁体的导热系数，W/(m·K)。

电机的电枢绕组包括铜芯和环氧树脂绝缘层等多种材料，因此式(11)中绕组的导热系数λsc可按如下公式计算[14]：

(12)

式中，vcur为电机的槽满率；λcu为铜的导热系数, W/(m·K)；λp为绝缘层的导热系数，W/(m·K)。

根据上述假设，电机空载时，等效定子的单位体积生热量qVS和等效转子的单位体积生热量qVR的计算公式如下：

(13)

式中，ps为定子铁耗，W；pm为永磁体内的涡流损耗，W；Vs为定子的体积，m3；Vsc为电枢绕组体积，m3；Vm为永磁体的体积，m3；Ve为等效定子单元的体积，m3；pR为转子铁耗，W；VR为等效转子单元体积，m3。

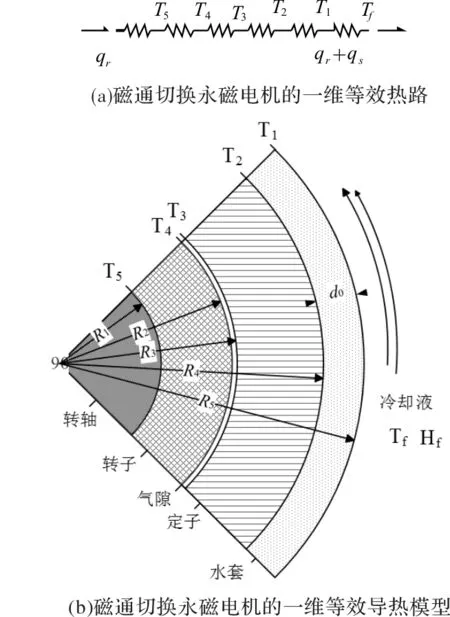
图6 磁通切换永磁电机的一维等效导热模型

由于本节只建立了电机的一维热路，故需要将定转子的单位体积生热量分别转化为定子单位长度生热量qs和转子单位长度生热量qr，其计算公式如下：

qs=qVSS1
qr=qVRS2

(14)

式中，S1为等效定子的横截面积，m2；S2为等效转子的横截面积，m2。

利用红外测温仪测量电机冷却结构进出口处的水温，两者相差不大，取两者的平均值作为水冷结构中水的近似温度Tf：

(15)

式中，Ti为水冷结构进口处的水温，K；To为水冷结构出口处的水温，K。

根据图6(a)所示的电机一维等效热路可得电机机壳的温度T1：

(16)

式中，Tf为流体的温度，K；hf为流体的对流散热系数，W/(m2·K)；R5为机壳外半径，m；R1为转子内半径，m；R3为定子内半径，m。

定子齿轭部的温度T2为

(17)

式中，R4为定子外半径，m；hf为机壳的导热系数，W/(m·K)。

圆柱坐标系下，有均匀内热源的导热微分方程和边界条件如下[15]：

(18)

式中，λr为转子的导热系数，W/(m·K)。

因此，将式(15)、式(16)、式(17)代入式(18)中，可得电机空载运行时，定子轭部的温度T3的计算公式：

(19)

如式(19)所示，当流体的平均流速增加时，冷却结构的对流散热系数增大，冷却结构的散热能力变强，定子的温度下降。 当电机运行于额定转速且空载时，改变电机冷却结构入口流量进行温升实验，验证上文推得的公式。实验结果如图7所示，当入口流速大于1.15m/s时，定子温度随着入口流速的增加而下降缓慢；从式(19)可知当入口流速大于1m/s时，定子温度随着入口流速的增加而下降缓慢，说明了上述数值分析的准确性。

4 水冷结构的优化分析

本文所研究的磁通换永磁电机在实际应用中，其输出功率通常为6kW，在混合动力平台上，给电机的水冷结构通入冷却水，进行电机温升实验，探究在该功率下电机的热性能，发现电机的最高温度高达116℃，且电机内的温升高达98℃，因而现有电机的冷却结构性能有待优化。

为了优化现有水冷结构的性能，本章利用Fluent软件仿真流道数和入口横截面积不同的水冷结构的流体场，仿真结果如图8所示。

从图8可知，当流道的高度或宽度横截面积增加时，其平均流速下降，这与前文的数值分析结果一致。并且当冷却结构流道数增加时，其平均流速增加。当冷却结构中的流速大于2.0m/s时，会加速流道的腐蚀，不利于冷却结构的安全稳定运行。因此图8(b)中，冷却结构的流速分布比较合理。

图8 不同几何参数的冷却结构流体场分布

利用有限元仿真得到冷却结构优化前后电机的温度场分布，如图9所示，当冷却结构优化后，定子齿部的温度下降。因此，相比现有水冷结构，优化后的水冷结构截面积减小，平均流速增加而且电机定子齿部的温度下降，其性能最优 。

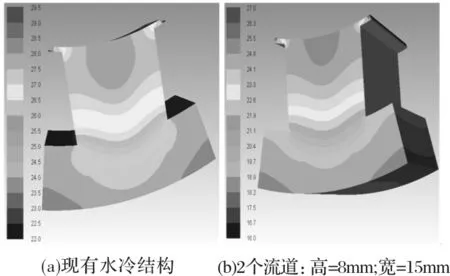
图9 不同冷却结构下定子和永磁体温度分布

综上所述，优化后的水冷结构几何参数如表4所示。

表4 优化后的水冷结构设计参数

5 结 论

由磁通切换永磁电机的温升实验可知，电机温度的最高点出现在绕组上。基于电机的一维等效热路，推导出电机径向温度分布与冷却结构几何参数间的数值关系，发现当冷却结构入口的横截面积减小或者流速增加时，电机定子齿部的温度降低。基于计算流体力学仿真，对电机现有冷却结构进行优化，提升了冷却性能。