基于优化承载能力的RV减速器摆线齿轮齿廓的等距-移距修形

陆龙生 张飞翔 唐 恒 万珍平 汤 勇

华南理工大学机械与汽车工程学院，广州，510640

0 引言

RV减速器在工业机器人[1-4]运行中发挥关键作用，对工业机器人的传动精度、承载能力和制造成本等具有重大影响[5-6]。它是一种新型的、二级封闭式、少齿差行星传动结构，由第一级渐开线行星轮系和第二级摆线针轮行星轮系复合而成，其中处于低速级的摆线针轮行星轮系对其传动效率、承载能力起着决定性的作用[7-8]。在摆线针轮行星轮系传动过程中，理论上针轮一半齿数可以与摆线轮的齿廓完全啮合，这样多齿同时啮合的特点可使RV减速器在运行过程中更加平稳、传动噪声更低、承载能力更大[9]。在实际应用中，通过对标准的摆线轮齿廓进行特定的修形，使运行过程中针齿销与对应啮合的摆线轮齿廓之间留有一定的齿侧间隙，这不仅可保证形成润滑作用的油膜，也有利于补偿RV减速器的制造和装配误差[10-11]。

然而，修形后的摆线轮存在齿侧间隙，这会使得针齿销和摆线轮啮合齿数减少，进而导致RV减速器整机承载能力降低，甚至会出现针齿磨损加速及针齿折断等使整机失效的严重问题[5,12]。由此可知，对摆线轮进行修形时，必须严格控制修形量，以减少针齿磨损和防止摆线针轮啮合质量降低。目前，常见的修形方式有3种：等距修形、移距修形和转角修形。在生产实践中，相比于单一修形方式，等距-移距组合修形方式效果更佳。对于修形量的确定，工程技术人员采取的方法不尽相同。何卫东等[13]通过逼近转角修形齿廓，得到了等距、移距修形时初始间隙的分布规律，这种通过负移距与负等距组合得到的修正齿形仅与转角修形齿廓齿形相似，但缺乏摆线针轮传动的啮合性能分析。REN等[14]通过设计齿侧间隙提出了啮合刚度最优的摆线轮修形方法。LIN等[15]分析了等距-移距组合修形对动态传动误差的影响，并以最小传动误差为目标确定了修形量。

承载能力是工业机器人中RV减速器最重要的性能之一。为进一步提高RV减速器的承载能力，合理选择摆线轮修形量，本文提出了基于优化承载能力的摆线轮等距-移距修形(以下简称“优化承载修形”)方法。对RV-40E减速器摆线轮标准齿廓进行了优化修形，并利用工程计算软件MATLAB进行求解，获得了承载能力最优的摆线轮齿廓曲线。对摆线轮的加工工艺进行了改进设计，加工制造出了优化承载修形摆线轮和作为对比验证的传统拟合转角修形摆线轮，并组装为对应的优化承载修形RV减速器样机和拟合转角RV减速器样机，通过分别进行承载能力测试，来验证优化承载修形方法在提高RV减速器传动效率和承载能力方面的优势。

1 数学建模

1.1 摆线轮的标准齿廓方程

RV减速器的结构和摆线针轮传动副啮合原理见图1，其摆线轮的标准齿廓方程可表示为[14]

(1)

K1=azp/rpiH=zp/zc

式中，rp为针齿中心圆半径；rrp为针齿半径；K1为短幅系数；a为偏心距；zp为针齿齿数；iH为摆线针轮副传动比；zc为摆线轮齿数；φ为针齿相对于转臂OcOp的转角。

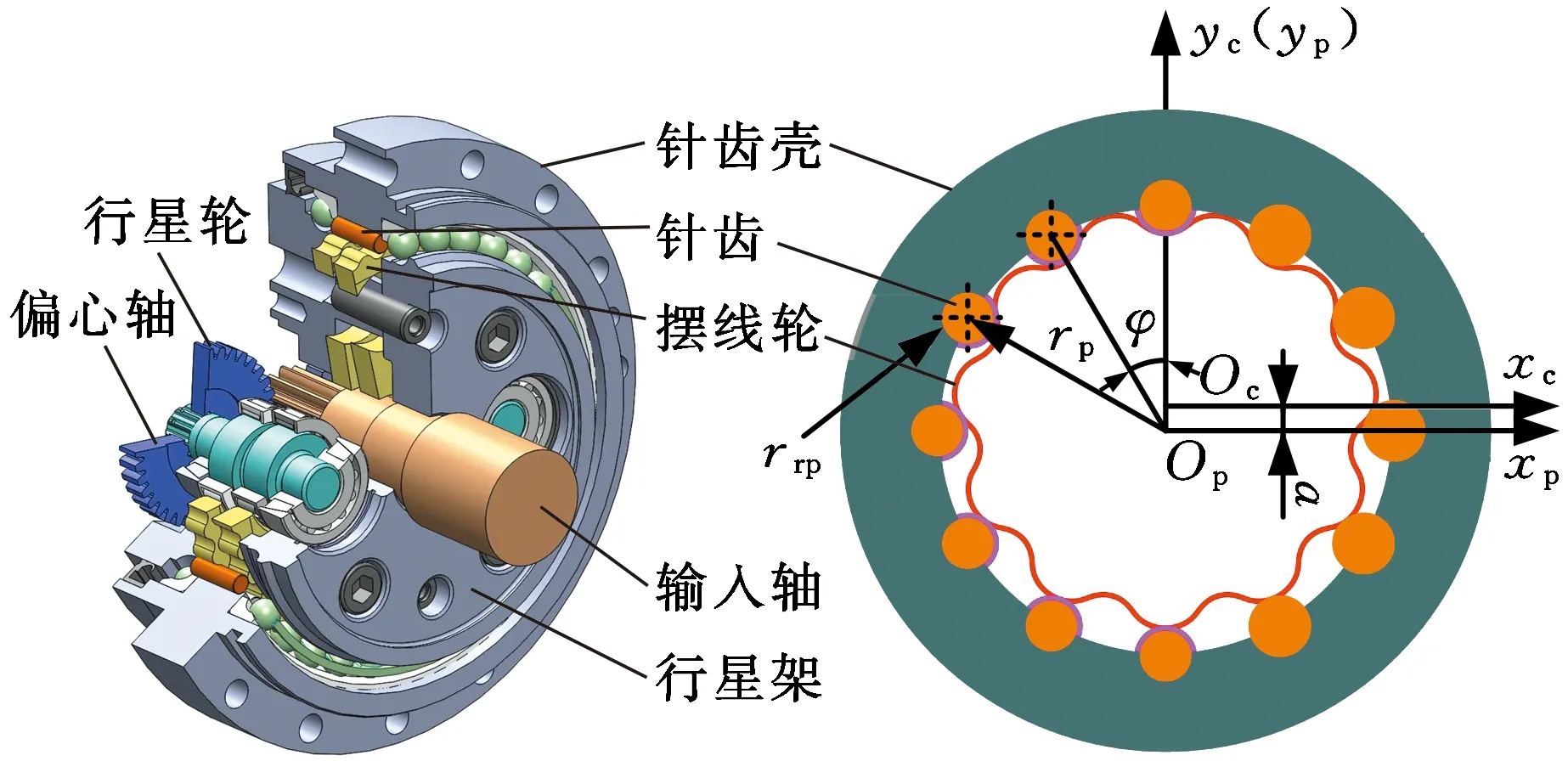
图1 RV减速器传动原理Fig.1 Transmission principle of the RV reducer

1.2 摆线轮齿廓优化承载修形的数学模型

为改善摆线轮与针齿的传动啮合质量、提高RV减速器的承载能力，综合等距修形和移距修形理论以及摆线轮传动受力分析，提出了一种搜寻等距、移距最佳修形量的方法(即优化承载修形方法)。

1.2.1优化变量

摆线轮齿廓修形方式采用在等距、移距修形基础上的组合修形，其优化变量可表示为

(2)

式中，Δrrp为等距修形量；Δrp为移距修形量。

1.2.2目标函数

RV减速器在运行过程中，其摆线齿轮与针齿销的啮合方式为多齿啮合，当第1个针齿与摆线轮接触时，针齿接触力最大，将此时的针齿法向接触力设为Fmax。在其他参数相同的条件下，摆线针轮传动的啮合齿数越多，Fmax越小，RV减速器及工业机器人的整机承载能力越大[5]。故将摆线针轮传动过程出现的最优承载能力设为寻优目标，将与摆线轮啮合传动时针齿最大接触力Fmax设为目标函数，则最佳修形量可表示为

f(Δrrp,Δrp)=min(Fmax)

(3)

1.2.3约束条件

为补偿RV减速器的制造误差，便于RV减速器的装配以及保证其良好的润滑，摆线轮和针齿之间必须留有一定的啮合间隙(包括径向间隙和齿侧间隙)。对于等距-移距组合修形，径向间隙Δr在数值上等于等距修形量Δrrp和移距修形量Δrp之和(即Δr=Δrrp+Δrp)。齿侧间隙Δs同样与等距修形量和移距修形量有关，是关于转角φi的函数Δs(φi)[15]，其表达式如下：

(4)

式中，φi为第i个针齿相对于转臂OcOp的转角。

在摆线轮的传动过程中，参与传动的针齿个数是一定的，因啮合面是连续的，故齿侧间隙Δs表示的是一个关于转角φi的连续函数。为便于计算和分析，将转角φi的初始值设定为100°，则根据式(4)，齿侧间隙的初始值可表示为

(5)

通过选择合适的等距修形量Δrrp和移距修形量Δrp，来确定合适的径向间隙Δr与齿侧间隙Δs，并最终实现摆线轮齿廓的优化承载修形。则在该条件下修形优化的约束条件满足：

(6)

2 求解及数值分析

传统的摆线针轮受力分析方法参见文献[6]。图2为摆线针轮传动力学分析图[16]，其中Oc、Op分别为摆线轮和针轮的几何中心。

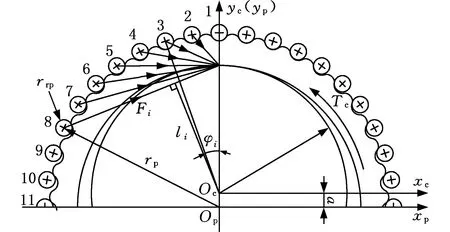
图2 摆线针轮传动力学分析图Fig.2 Force analysis diagram of cycloidal drive

对摆线针轮传动进行受力分析时，在传统的摆线针轮受力分析的基础上作了如下两点改进。

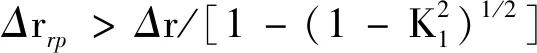
(2)形变量的求解。在RV减速器中，由于针齿固定在针齿孔中，它在啮合过程中几乎不发生弯曲变形，因此在分析针齿受力后的形变时，只需考虑其接触形变。

基于上述两点改进后对图2进行受力分析，设RV减速器受到的负载扭矩为Tc，则该条件下目标函数Fmax的求解步骤可由如下五大主要步骤完成[18]。

(1)输入减速器的参数和修形量，确定受力最大的针齿位置和啮合点，计算该啮合点的公法线到摆线轮的中心Oc的距离lmax。

(2)计算针齿最大接触力的初始值Fmax0。通过迭代求解的方法确定修形后摆线针轮传动中同时啮合的齿数和Fmax的精确值。针齿最大接触力初始值的计算表达式如下：

(7)

(3)计算受力最大针齿啮合点的法向位移δmax。在实际运行过程中，摆线轮与针齿之间的接触属于典型的赫兹接触，由赫兹公式[13]可得

(8)

式中，μ1、μ2分别为摆线轮材料和针齿材料的泊松比；E1、E2分别为摆线轮材料和针齿材料的弹性模量；b为摆线轮的有效宽度；ρ为摆线齿廓的曲率半径。

(4)通过比较啮合点形变量δi与齿侧间隙Δs(φi)的大小，来确定同时啮合的针齿对数。其中，啮合点形变量的表达式如下：

(9)

式中，li为第i个针齿啮合点的公法线到摆线轮中心Oc的距离。

根据式(9)，当啮合点形变量δi大于该位置的齿侧间隙Δs(φi)时，该针齿与摆线轮齿将啮合；反之，则针齿与摆线轮齿之间存在间隙。

(5)计算针齿最大接触力Fmax。摆线轮通过与第i个针齿imesh啮合，进而传递运行过程中的扭矩，当修形摆线轮与针轮进行有隙啮合时，第i个啮合点的接触力Fi与δi-Δs(φi)成近似正比关系，且δi与li成正比[16]。针齿最大接触力的计算表达式如下：

(10)

根据式(7)和式(10)比较Fmax和Fmax0的大小：若Fmax≠Fmax0，则判定Fmax没有收敛，需重新进行迭代求解，并将Fmax的值赋予Fmax0，返回步骤(3)；若Fmax=Fmax0，则判定Fmax收敛，输出收敛解Fmax。

确定Fmax的求解步骤后，摆线针轮传动承载能力最优的最佳修形量可依据优化设计理论进行求解。在径向间隙Δr=Δrrp+Δrp确定的条件下，寻优求解转变成一维最优化问题，自变量设置如下：等距修形量设为Δrrp，移距修形量则为Δrp=Δr-Δrrp。采用格点法进行求解，根据齿侧间隙Δs>0来寻找等距修形量的优化区间，并利用m个等分点，将搜索区间划分成m+1个子区间。计算目标函数在各个等分点的函数值，并通过比较得到它们的最小值min(Fmax)。综上所述，该数学模型的求解步骤见图3。其中，ε为计算得到的针齿最大接触力Fmax与其初始值Fmax0的收敛判断误差，计算时设ε=0.01 N；T为减速器额定负载扭矩。

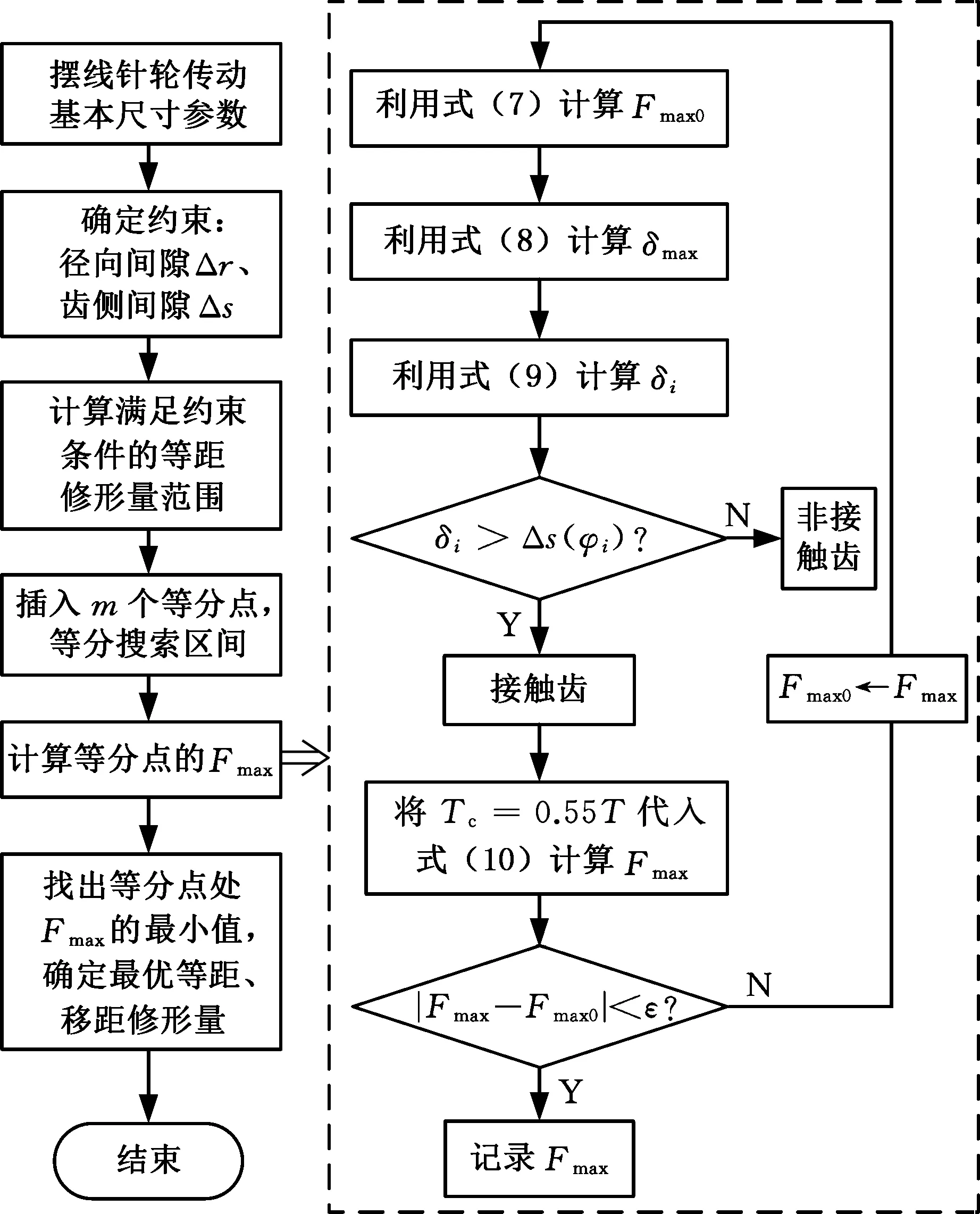
图3 优化模型求解步骤Fig.3 Optimization model solving steps

利用MATLAB软件进行寻优计算，可分别求解得到等距修形量Δrrp和移距修形量Δrp。则优化修形后的摆线轮齿廓方程可表示为

(11)

3 实例分析

3.1 优化承载修形齿廓方程的建立

目前RV-40E减速器广泛应用于工业机器人领域，因此本节以该款减速器为研究对象进行摆线轮齿廓的优化设计，其主要几何参数见表1。通过将径向间隙和齿侧间隙与该原装减速器的相应间隙设置一致，从而保证优化承载修形方法的实际对比效果。利用MarSurf XCR 20轮廓扫描仪扫描该原装摆线轮的部分齿廓，以准确地获得径向间隙和齿侧间隙，将扫描坐标点输入到Gleason 350GMM齿轮检测中心，测出该原装摆线轮齿廓的齿形尺寸，通过将其与摆线轮标准齿廓进行对比，可得到原装摆线轮齿廓的径向间隙Δr=0.225 mm，齿侧间隙Δs(100°)=0.029 mm。

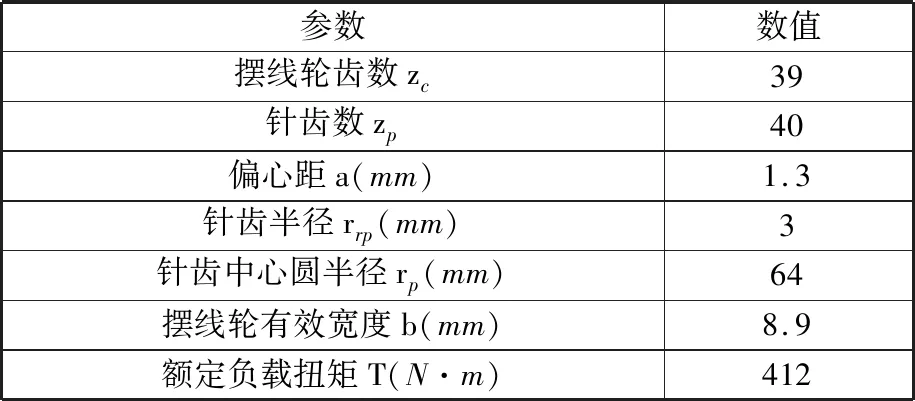
表1 摆线针轮传动的主要几何参数Tab.1 Main geometric parameters of cycloidal drive

依据Δs(φi)>0，计算得到等距修形量的搜索区间为[0,0.596 9 mm]。在搜索区间内插入5 000个等分点，并将搜索区间分为5 001个大小相等的子区间。采用MATLAB软件编写程序计算等分点处的目标函数值。以等距修形量Δrrp=0.225 mm，移距修形量Δrp=Δr-Δrrp=0时为例，则目标函数Fmax的计算过程具体如下。

(1)已知等距修形量Δrrp=0.225 mm，依据图2和表1中的摆线轮几何参数，可以确定最大受力针齿为第5号针齿，并得到lmax=50.7 mm。

(2)计算针齿最大接触力初始值Fmax0。RV-40E减速器的额定负载扭矩T由2个摆线轮进行传递，考虑到制作和安装产生的误差会引起摆线轮之间的载荷分配不均匀，取实际受到的负载扭矩Tc=0.55T。由式(7)可得Fmax0≈447 N。

(3)计算受力最大针齿啮合点的法向位移δmax。摆线轮和针齿的材料分别为20CrMo和GCr15，对于20CrMo材料，其泊松比和弹性模量分别为0.278和 210 GPa；对于GCr15材料，其泊松比和弹性模量分别为0.3和206 GPa。由式(8)可得δmax=4.449 9 μm。

(4)通过比较各针齿啮合点形变量δi与齿侧间隙Δs(φi)的大小，来确定同时啮合齿对数。得到同时啮合齿为第4～6号齿，则同时啮合齿对数为3。

(5)计算针齿最大接触力Fmax。由式(10)可得Fmax=4 748.1 N。

由于Fmax=4 748.1 N≠Fmax0，表明Fmax不收敛，因此将Fmax的值赋予Fmax0，并返回步骤(3)继续运算。经过21次迭代计算，求出目标函数值为2 339.5 N。

按照上述计算步骤，计算并比较所有等分点处的目标函数值，得到最佳修形量如下：等距修形量Δrrp=0.550 mm，移距修形量Δrp=-0.325 mm。则优化后的摆线轮齿廓方程可表示为

(12)

3.2 承载能力数值分析

在径向间隙相同的情况下，利用改进的摆线针轮受力分析方法来分别计算不同修形方法下的摆线针轮副承载能力。表2所示为4种修形方法的承载能力对比，可以看出，RV-40E中的摆线轮经优化承载修形后，摆线针轮传动中的针齿最大接触力为1 420.2 N，同时啮合齿对数为8。相比其他3种修形方式，该优化承载修形方式的针齿最大接触力最小，啮合齿数最多，其针齿最大接触力分别是等距修形方式、移距修形方式、拟合转角修形方式的针齿最大接触力的60.7%、52.2%和90.0%。

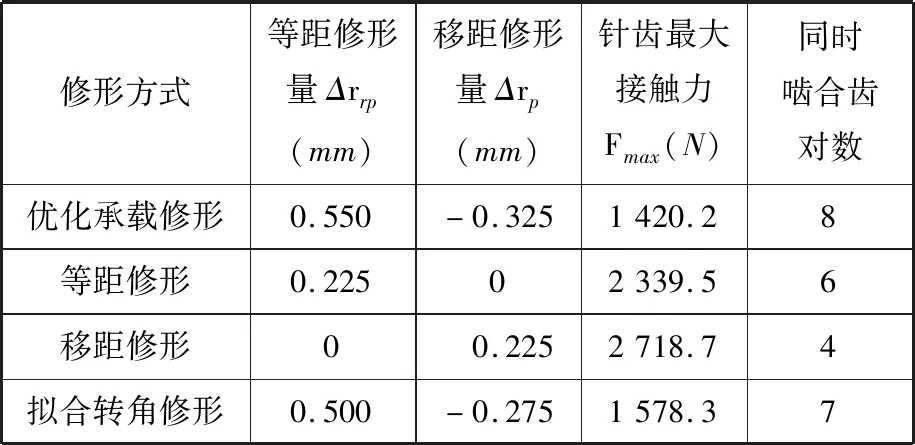
表2 4种修形方法下的摆线针轮传动承载能力对比Tab.2 Comparison of the capacity of cycloidal drive on four modification methods

由表2可知，上述4种修形方法下的摆线针轮传动副承载能力不同，这是因为不同修形方法采用的等距修形量、移距修形量不同。通过对不同等距修形量、移距修形量下的针齿最大接触力和啮合齿数进行数值计算，可进一步分析得到不同的修形量对承载能力的影响，计算所得结果见表3。

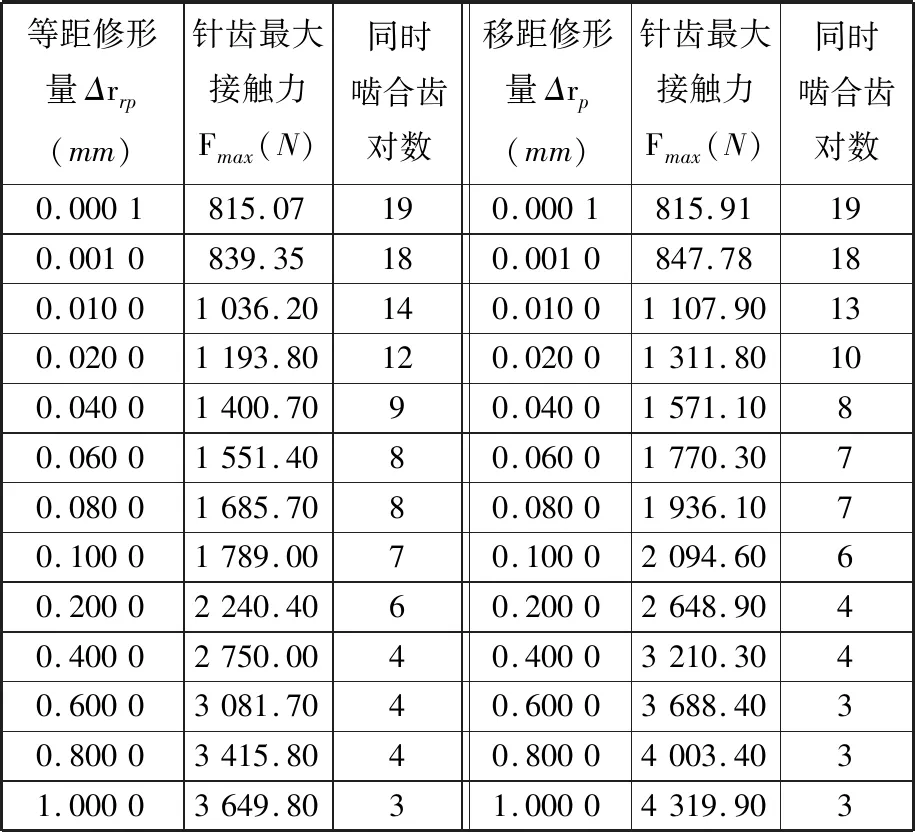
表3 修形量对摆线针轮传动承载能力的影响Tab.3 Influence of the modification amount on the capacity of cycloidal drive

由表3可知，修形量对针齿最大接触力和同时啮合齿对数产生的影响显著，针齿最大接触力随着修形量的增大而增大，同时啮合齿对数随着修形量的增大而减小。在相同修形量的情况下，与等距修形方式相比，移距修形方式会产生更大的针齿最大接触力。对于同一个标准齿廓的摆线轮，若采用单一的等距修形或移距修形方式，当修形量增大到1 mm时，同时啮合齿对数仅为3，不到针齿数的1/10；当修形量为0.001 mm时，虽然同时啮合齿对数达到了18，但此时的径向间隙为0.001 mm(过小)，无法满足摆线轮装配与润滑的要求。由此可知，只有修形量选择合理的等距-移距组合修形，才可在满足较大径向间隙的要求下，确保一定数量的同时啮合齿对数和合理的针齿接触力。

综上可知，采用基于优化承载能力的RV减速器摆线轮齿廓的等距-移距修形方法可得到合适的修形量，进而可改善运行过程中摆线轮的啮合性能，并提高其承载能力。

4 摆线轮试样制造与承载能力试验

通过对摆线轮的加工工艺进行优化设计，加工制造出优化承载修形摆线轮和用来作对比验证的拟合转角修形摆线轮，并将两种摆线轮分别组装成相应的RV减速器样机，通过对优化承载RV减速器样机、拟合转角RV减速器样机进行性能测试和对比，以验证所提优化承载修形方法的实用性。

4.1 摆线轮试样制造

根据基于优化承载修形方法的摆线轮齿廓方程(式(12))，采用慢走丝线切割合金结构钢20CrMo毛坯得到具有优化承载摆线轮齿廓的摆线轮工件，将线切割得到的摆线轮经过一定的热处理加工，并利用美国Moore 450CP精密磨床磨削加工成形，得到具有优化承载能力的摆线轮。摆线轮(韶能集团宏大齿轮有限公司制造)加工工艺见表4，图4为加工完成后得到的摆线轮实物图。

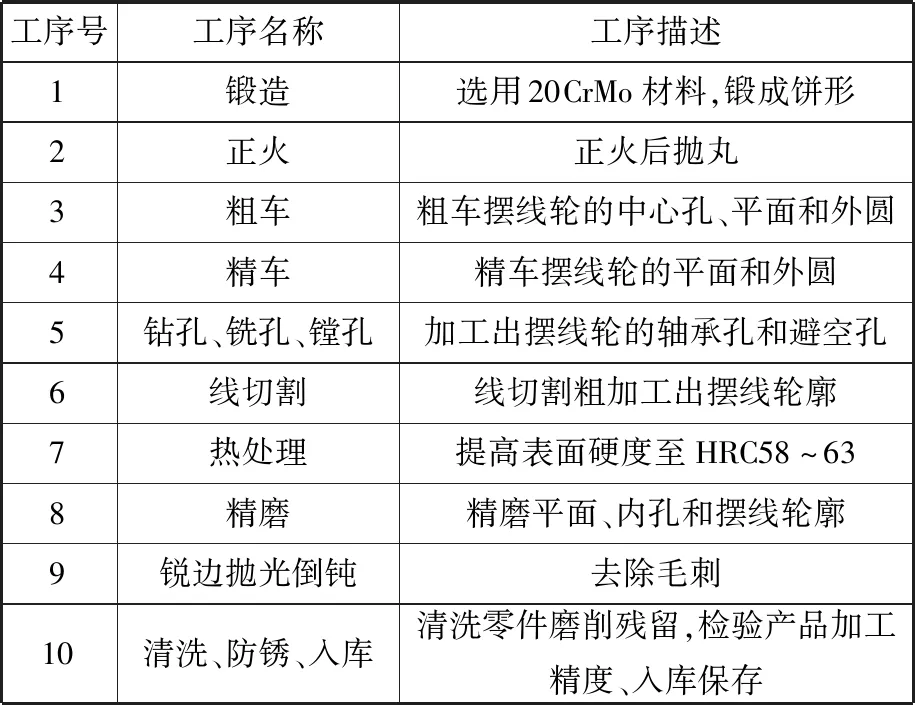
表4 摆线轮加工工艺Tab.4 Processing technology of the cycloid gear

图4 摆线轮实物图Fig.4 The cycloidal gear

对优化承载修形摆线轮的实际使用性能进行检验，将其替换为RV-40E的原装摆线轮，装配后进行样机综合传动性能测试，主要包括测试其刚性、齿隙、承载能力以及在不同载荷下的传动效率、温升。图5所示为装配后的待测RV减速器。

图5 待测RV减速器Fig.5 The RV reducer for testing

4.2 试验设备与测试方案

根据我国机械行业标准JB/T 5288.3-1991《摆线针轮减速机承载能力及传动效率测定方法》，在图6所示的RV减速器承载能力测试台(韶能集团宏大齿轮有限公司制造)上对RV减速器承载能力及传动效率进行测试。承载能力由轻载试验、额定负载试验和重载试验下的效率、噪声、温升等性能指标体现。轻载试验可体现出RV减速器装配质量；额定负载试验和重载试验可分别体现出RV减速器在额定负载及重载状态下的工作性能。

图6 承载能力测试台Fig.6 The carrying capacity test table

加载测试开始之前，测试台需要空载运行2 h以上，并保证RV减速器输出转速稳定在15 r/min。在距RV减速器20 mm处，利用SMART噪声测试仪AR824检测噪声，利用SMART红外线测温仪AR300检测输出盘温度，并测试多组数据取平均值。

4.3 试验结果

本文分别对优化承载RV减速器、拟合转角RV减速器、日本帝人RV减速器进行了承载能力测试，设置被测RV减速器的试验条件如下：输出转速15 r/min，测试前保持室温25 ℃，轻载试验、额定负载试验和重载试验下的负载扭矩分别为100 N·m、412 N·m和1 000 N·m。图7～图9所示分别为传动效率测试结果、噪声测试结果和输出盘温升测试结果。

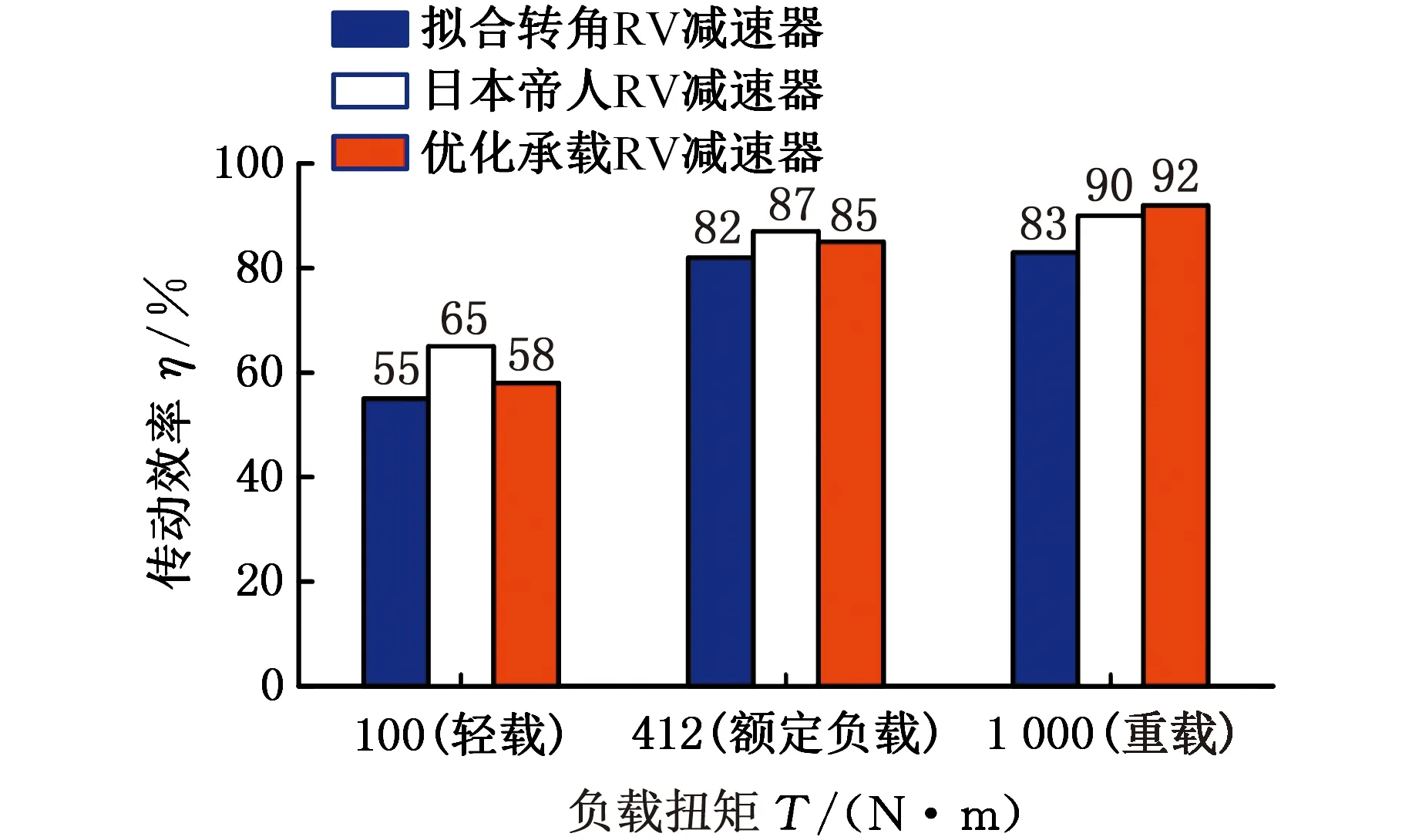
图7 传动效率测试结果Fig.7 Test results of transmission efficiency

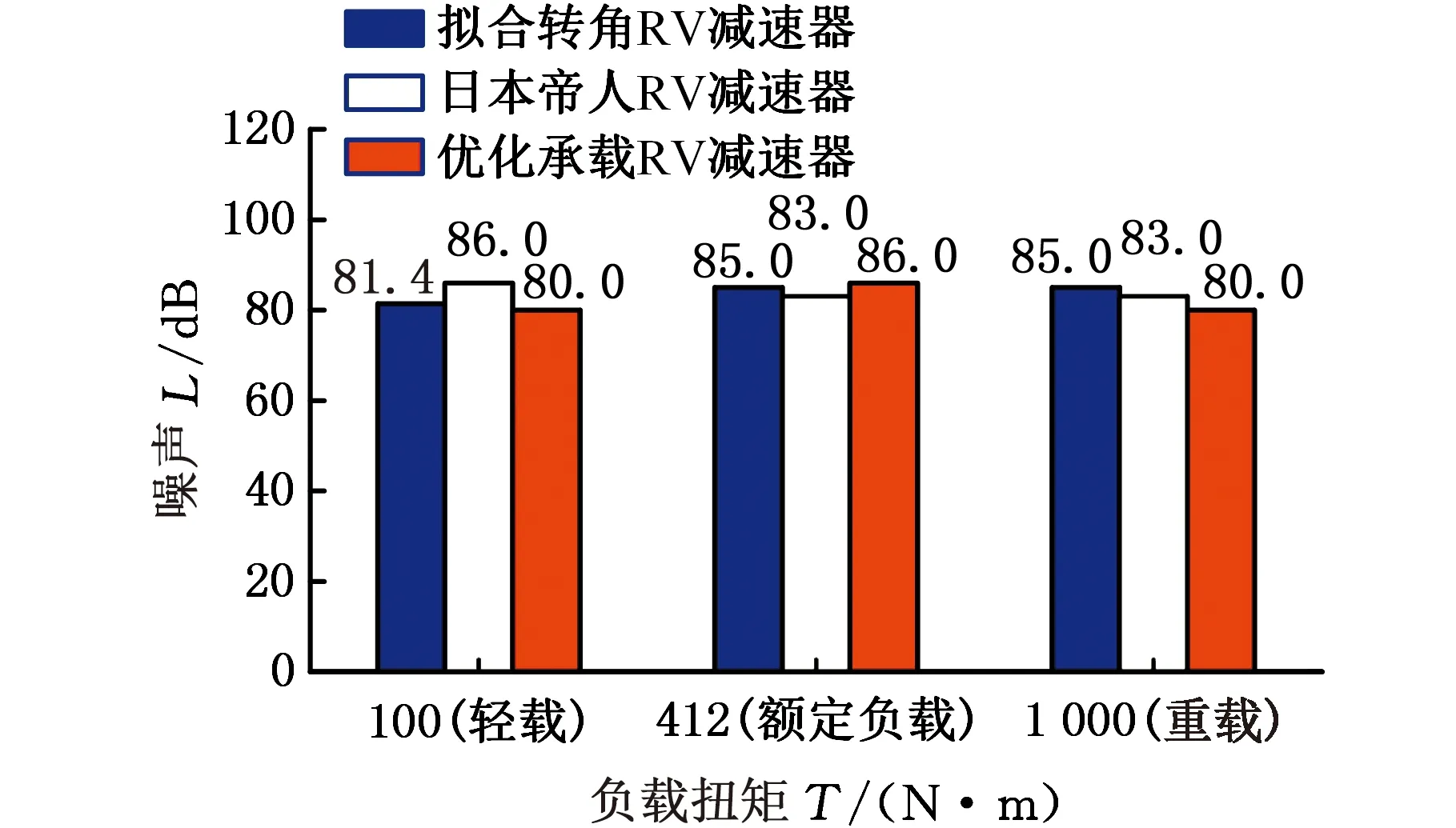
图8 噪声测试结果Fig.8 Test results of noise

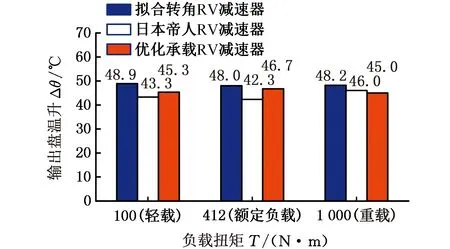
图9 行星架(输出盘)温升测试结果Fig.9 Test results of temperature rise of a planetary frame(output plate)

从图7～图9中可以看出，在不同负载条件下，3种类型的RV减速器均表现出了良好的性能。传动效率随着负载扭矩的增大呈现增大的趋势。在轻载、额定负载条件下，优化承载RV减速器的传动效率分别为58%和85%，比拟合转角RV减速器在对应负载扭矩下的传动效率均提高了3%。传动过程中的功率损失随着传动效率的提高而减小，热能损耗减少。在额定负载运行条件下，优化承载RV减速器的输出盘温度稳定在46.7 ℃，比拟合转角RV减速器的输出盘温度降低1.3 ℃。在重载条件下，优化承载RV减速器相比于日本帝人RV减速器，其传动效率更高，达到了92%。随着传动效率的提高，优化承载RV减速器在负载相同的情况下转换成热量的能量损耗减少，输出盘温度保持在45 ℃左右，其噪声比日本帝人RV减速器的噪声降低了3 dB，表现出了更好的啮合性能，这也体现了基于优化承载能力的RV减速机摆线轮齿廓的等距-移距修形方法具有更优的承载能力和良好的实用性。

5 结论

(1)提出了具有优化承载能力的RV减速器摆线轮齿廓的等距-移距修形方法，建立了以承载能力最优为目标函数的摆线轮齿廓最佳修形量数学模型。将数学模型进行一维简化及迭代计算，从而求解得到了最佳修形量。

(2)以工业机器人的RV-40E减速器为研究优化对象，采用优化承载修形方式后，当针齿最大接触力为1 420.2 N、与摆线轮同时啮合齿对数为8时，针齿最大接触力最小，啮合齿数最多，该优化条件下的针齿最大接触力分别是等距修形、移距修形、拟合转角修形方式针齿最大接触力的60.7%、52.2%、90.0%。

(3)对优化承载RV减速器、拟合转角RV减速器、日本帝人RV减速器分别进行承载能力测试，试验结果表明：在轻载、额定负载条件下优化承载RV减速器的传动效率分别为58%和85%，比拟合转角RV减速器在相同条件下的传动效率均提高了3%。在额定负载运行条件下，优化承载RV减速器的输出盘温度稳定在46.7 ℃，比拟合转角RV减速器的输出盘温度降低了1.3 ℃。在重载情况下，与日本帝人RV减速器相比，优化承载RV减速器的传动效率更高，可达到92%，噪声降低了3 dB，其输出盘温度保持在45 ℃左右，从而验证了所提优化承载能力修形方法具有良好的实用性。