列车车体SUS301L-HT不锈钢动态力学性能及其对结构吸能特性的影响
陈书剑 程 迪 肖守讷 朱 涛 阳光武 杨 冰 冯 悦
1.西南交通大学牵引动力国家重点实验室,成都,6100312.郑州铁路职业技术学院机车车辆学院,郑州,451460
0 引言
列车车体结构在碰撞过程中会发生大变形,车体材料在塑性区的动态力学性能对车体结构的变形和吸能有很大影响[1]。研究结果表明,材料应变率效应对结构的碰撞响应特性有显著的影响[2-3]。当列车发生碰撞事故时,所产生的塑性大变形集中在车辆前端1/10内,车辆主体几乎不变形,列车前端的吸能结构吸收了绝大部分动能[4]。由此可知,列车吸能结构的动态冲击响应能够充分反映列车的碰撞情况,其吸能特性很大程度上决定了列车的被动安全性。但目前针对应变率效应对列车吸能结构碰撞响应的研究较少,且不够深入[5-9]。
对于车体常用金属材料,通常采用动态本构模型来描述其动态力学行为。文献[10-12]均利用Johnson-Cook(J-C)模型对铝合金动态力学行为进行研究。文献[13-15]的研究发现,钢是应变率敏感材料,20钢、双相钢、低合金高强度冷轧钢 HC340LA均表现出了明显的应变率强化效应。文献[16]针对0Cr17Mn5Ni4Mo3Al不锈钢,利用修正后的J-C模型可使拟合曲线与实验曲线具有较好的一致性。文献[17]在不同拉伸速率条件下对SUS304不锈钢拉伸力学行为进行研究。文献[1,15]指出,J-C模型或Cowper-Symonds(C-S)模型在进行拟合时具有一定缺陷,即便对模型进行了修正也无法描述某些材料的特殊性质,这是因为J-C模型或C-S模型仅选取了某个塑性应变下的一组流动应力进行拟合标定,丢失了大量的试验有效数据,所以拟合的应变率本构方程具有一定的应用局限性。为了更准确地描述材料的动态力学性能,文献[1,15]均采用了列表插值法,但均未进行更深入的研究。
不锈钢中各化学元素种类及其所占百分比的改变会使材料的动态力学性能产生巨变,且目前有关车用SUS301L系列不锈钢动态力学行为的研究相对较少,因此很有必要对车用SUS301L-HT不锈钢的动态力学性能进行研究。据统计,列车的碰撞事故基本上都是在中低速运行时发生的,所以研究车用材料在中低应变率下的力学性能更具有实际意义[9]。
本文以SUS301L-HT不锈钢为研究对象,分别对其进行准静态拉伸试验和动态拉伸试验,通过试验数据得到不同中低应变率下的SUS301L-HT不锈钢应力-应变曲线,并研究了该材料的动态力学行为,分析对比了J-C模型、C-S模型和列表插值法三种方法对SUS301L-HT不锈钢应变率本构方程的拟合效果。针对SUS301L-HT不锈钢材料特有的动态力学性能,研究了列表插值法的本质,并分析了SUS301L-HT不锈钢材料应变率效应对结构吸能特性的影响。
1 材料与试验方法
本试验材料为不锈钢车体的主要材料SUS301L-HT,该材料具有强度高、抗腐蚀性能优良的特点[18]。准静态试验在MTS Bionix858微力拉扭材料试验机上进行。试验应变率范围为0.1~500 s-1(即中低应变率情况),为确保应变测量结果的准确性,动态拉伸试验采用数字图像相关(digital image correlation,DIC)非接触式应变场测量方法,并在Zwick/Roell的HTM5020试验机上进行。试验的准静态与动态拉伸试件分别见图1和图2。

图1 SUS301L-HT不锈钢准静态拉伸试样Fig.1 Quasi-static tensile test specimen of SUS301L-HT stainless steel
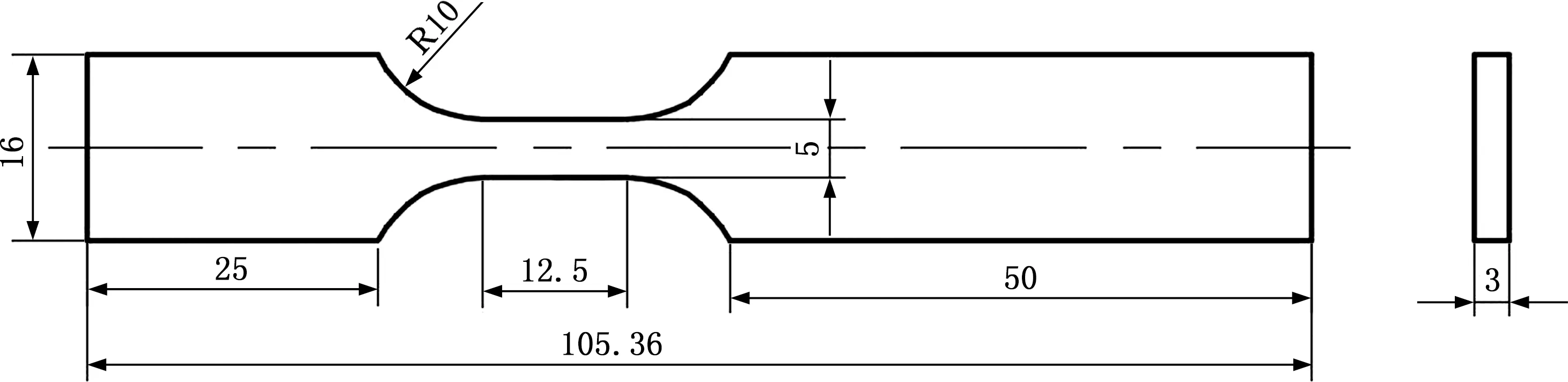
图2 SUS301L-HT不锈钢动态拉伸试样Fig.2 Dynamic tensile specimen of SUS301L-HT stainless steel
2 试验结果分析
(1)
式中,εe为工程应变;σe为工程应力;εt为真实应变;σt为真实应力。
图3给出了不同应变率下,准静态拉伸和动态拉伸试验的真实应力-应变曲线。由图3可知,SUS301L-HT不锈钢的拉伸应力-应变动态响应表现出了典型的非线性弹塑性变形特征,应变硬化能力较强,无明显屈服点;随着应变率数量级的增大,材料的屈服强度明显提高,0.1~500 s-1应变率下的应力-应变曲线明显高于准静态下的曲线,且表现出了明显的应变率强化效应,但材料开始出现颈缩时所对应的塑性应变随着应变率的增大而减小,这表明SUS301L-HT不锈钢材料不具备应变率增塑的效应,应变率的增大导致曲线可达到的最大应变值逐渐减小(即失效应变减小)。
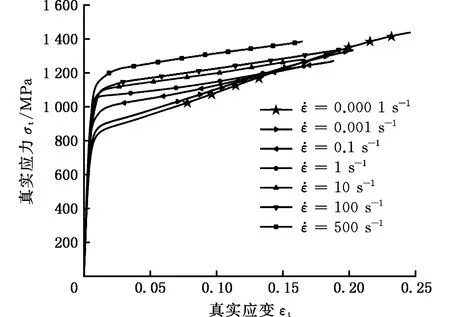
图3 SUS301L-HT不锈钢准静态和动态拉伸试验结果Fig.3 Quasi-static and dynamic tensile test results of SUS301L-HT stainless steel
应变率增大的同时,材料曲线在塑性段趋于平缓,动态拉伸应力-应变曲线与准静态曲线相交,呈明显闭口形态,材料的塑性硬化能力明显降低。动态拉伸试验过程中,试件在短时间内发生塑性大变形进而产生热量,除去试件与外界发生热交换而散失的少部分热量,随着塑性变形的增大,材料温度会持续升高,从而导致流动应力同时减小,表现出了明显的温度软化效应。这与尚兵等[16]对0Cr17Mn5Ni4Mo3Al不锈钢动态本构的研究结果基本一致。参见文献[19],试件温升可利用下式进行计算:
(2)
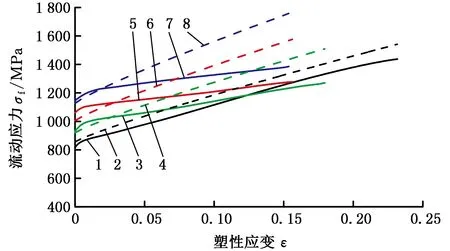
式中,ΔT为试件的温升;ε为试件塑性应变;β为塑性功转化为试件温升的百分比系数,当材料塑性应变大于0.2时,一般取β=1[20];σf为流动应力;ρ′为材料密度,取ρ′=7.93 g/cm3;cm为室温下的质量热容,取cm=500 J/(kg·K)。
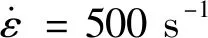
在上述两种效应的共同作用下,虽然应变率强化效应显著增大了同一塑性应变下材料的流动应力,但同时也增强了温度软化效应,使得流动应力随着塑性应变的增大,其增大的速率减小,最终流动应力在闭口点前被强化(即流动应力值增大),在闭口点后反而小于准静态应力值。
3 动态力学性能的描述
基于试验的动态本构关系理论在工程中应用较为普遍的有基于过应力理论的C-S模型和基于黏塑性模型理论的J-C模型[21]。上述两种动态本构模型均采用准静态项与应变率影响项以乘积相耦合的形式,其具体形式分别如下:
C-S模型:
(3)
J-C模型:
(4)
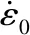
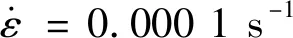
试验拟合 试验拟合 试验拟合 试验拟合图4 Johnson-Cook模型拟合的应力-应变曲线与试验结果的比较Fig.4 Comparison of the stress-strain curves fitted with the Johnson-Cook models under different strain rates with the testing results
试验拟合 试验拟合 试验拟合 试验拟合图5 Cowper-Symonds模型拟合的应力-应变曲线与试验结果的比较Fig.5 Comparison of the stress-strain curves fitted with the Cowper-Symonds models under different strain rates with the testing results
由拟合结果可知,无论是C-S模型或J-C模型,均无法准确地描述SUS301L-HT不锈钢随着应变率的增大,其塑性硬化能力逐渐降低的特征;这两种动态本构模型实质上均为材料在准静态下拟合后,由一系列不同应变率项线性放大后得到的结果,且放大后得到的结果均有发散性,因此不能得到呈闭口状的动态应力-应变曲线。此外,J-C模型和C-S模型仅选取了某个塑性应变下的一组流动应力进行拟合标定,大量试验的有效数据均未参与分析,因此拟合得到的应变率本构方程精确性较差。
在工程应用上,为充分利用试验数据并保证结果的准确性,通常采用列表插值法来描述SUS301L-HT不锈钢这种特殊材料的动态力学性能。列表插值法在每一应变率下定义一条载荷曲线,该载荷曲线即为该应变率下材料的塑性应变与其流动应力间的函数。未知流动应力由相邻离散流动应力之间的插值获得,如图6所示。列表插值法分为列表线性插值法和列表对数插值法。通常为节省计算时间,采用列表线性插值法进行分析,但必要时,需采用列表对数插值法,以提高列表插值法的精度。上述两种方法的流动应力计算公式分别如下:
列表线性插值法:
(5)
列表对数插值法:
(6)
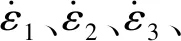
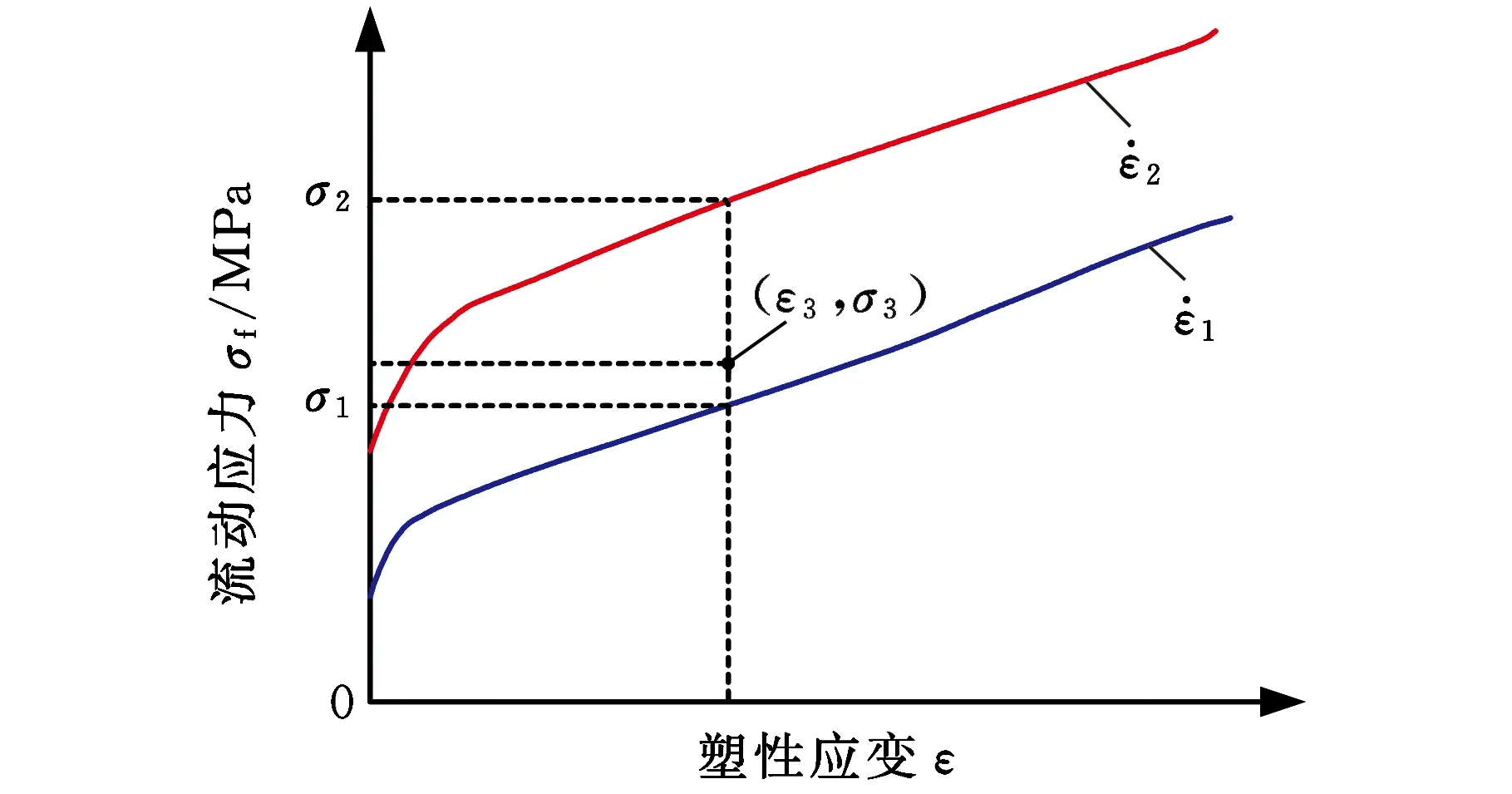
图6 列表插值法原理Fig.6 Principle of tabular interpolation method
为验证列表插值法的准确性与适用性,任选一应变率对其载荷曲线进行插值,其他不同应变率同理进行分析。现假设已知1 s-1和100 s-1应变率下的试验载荷曲线,采用列表插值法对应变率为10 s-1的载荷曲线分别进行线性插值和对数插值,并与10 s-1应变率下的试验结果进行对比,见图7。
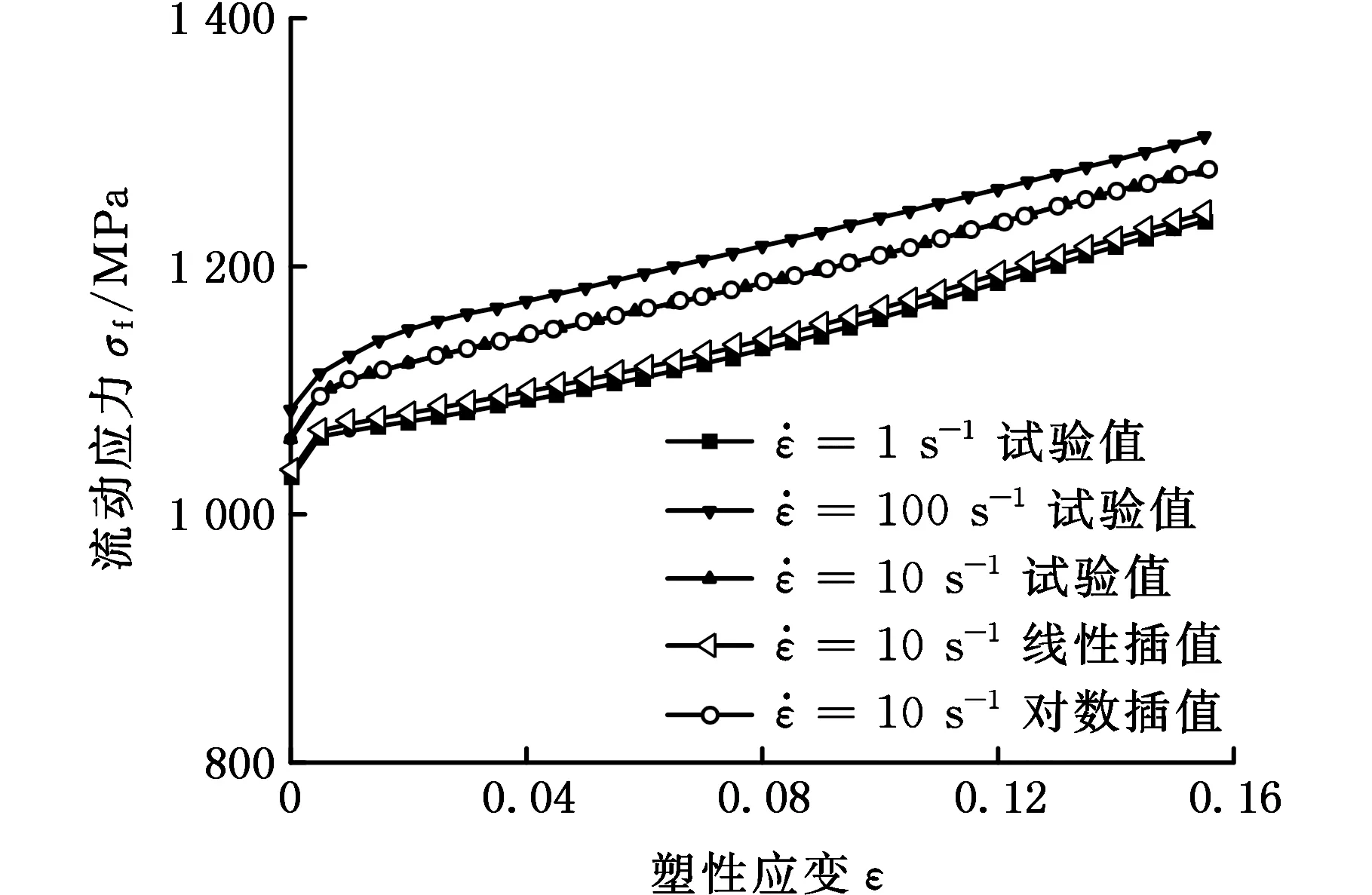
图7 列表插值法得到的应力-应变曲线与试验结果的比较Fig.7 Comparison of stress-strain curves obtained from table interpolation method and testing results
结合图4、图5和图7可知,列表插值法能更好地描述SUS301L-HT不锈钢的动态力学性能,插值得到的结果与试验结果吻合度高,能适用于有限元仿真。但采用列表线性插值法得到的载荷曲线与试验载荷曲线相比偏低,虽然采用列表对数插值法得到的结果与试验结果具有良好的一致性,但在进行有限元计算时,调用对数插值法需要额外的计算成本,且增加了计算时间。
为验证列表插值法的准确性,可采用LS-DYNA软件进行有限元模拟对标。按照实际尺寸对试件采用实体单元的有限元建模。试件的边界条件见图8,试件固定段被完全约束,试件加载段被赋予恒定的拉伸速度,载荷边界条件与试验时保持一致。
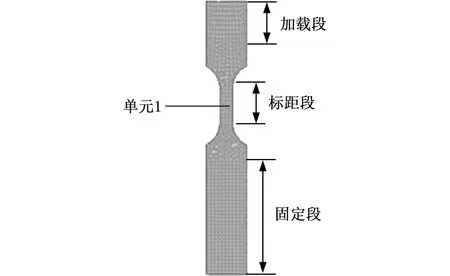
图8 试件有限元试验Fig.8 Finite element method of SUS301L-HT stainless steel
为预测SUS301L-HT不锈钢在10 s-1应变率下的应力-应变关系,有限元计算时采用*DEFINE_TABLE方法定义除10 s-1应变率外的所有试验曲线,并对比单元1输出的应力-应变曲线、列表插值曲线和试验曲线。如图9所示,在误差范围内,列表线性插值结果与有限元结果的趋势基本一致,这验证了列表线性插值法的可靠性;但两者所预测10 s-1应变率下的流动应力值均小于试验结果的流动应力值,此为列表线性插值法存在的不足。虽然列表线性插值法不受材料动态本构关系变化趋势的影响,但若材料各数量级应变率下的同一塑性应变的流动应力不呈线性缩放,则采用列表线性插值法也会产生一定误差。
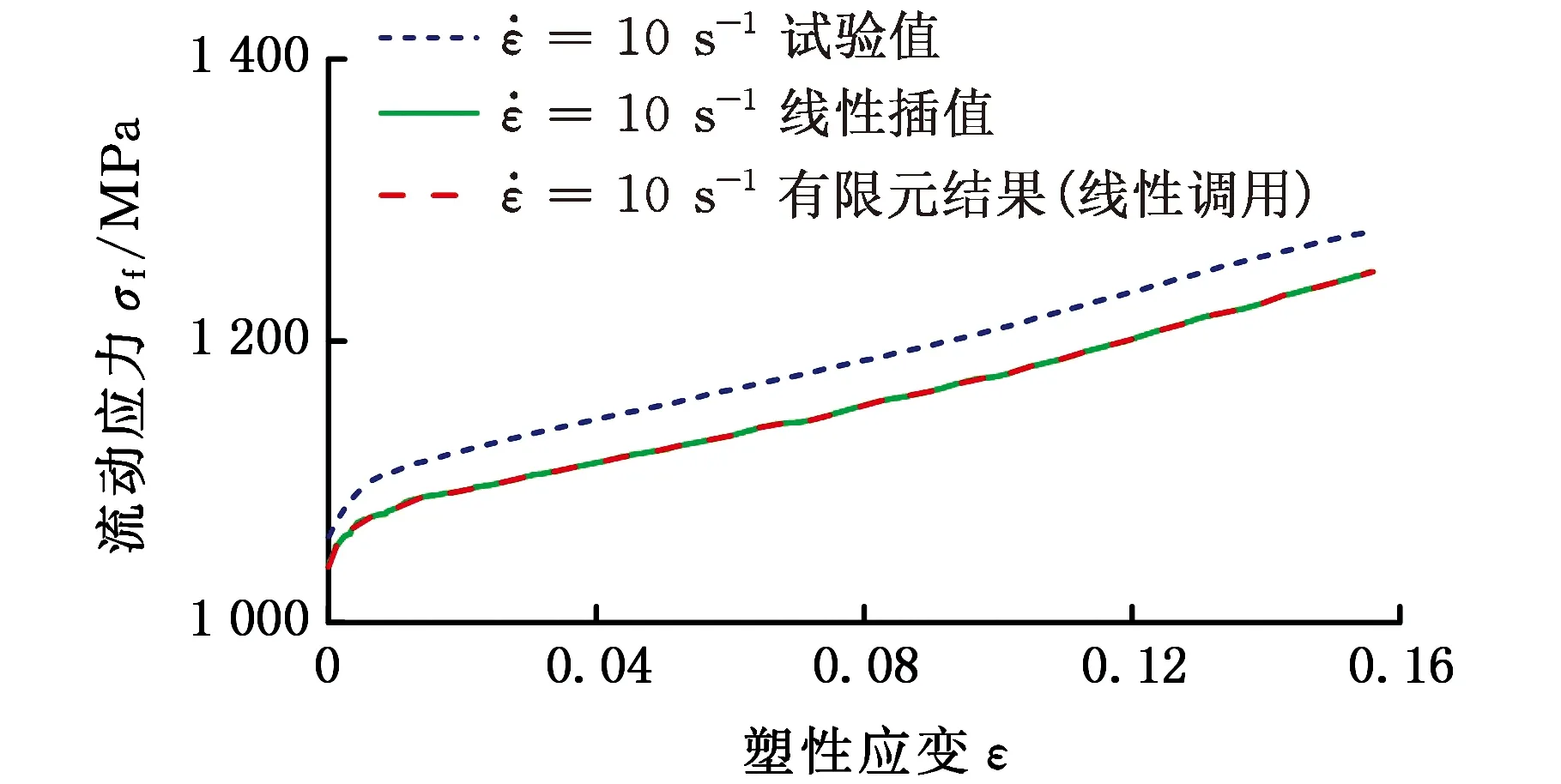
图9 线性插值、有限元仿真与试验结果的比较Fig.9 Comparison of linear interpolation, finite element simulation and testing results
为作对比分析,在*DEFINE_TABLE中输入各数量级应变率的自然对数,调用对数内插,图10所示为对数插值方法与试验值的对比结果。由图10可以看出,采用列表对数插值法和有限元模拟中对数插值法,预测SUS301L-HT不锈钢在10 s-1应变率下的流动应力值,研究发现两种方法得到的结果均与试验结果具有一致性。
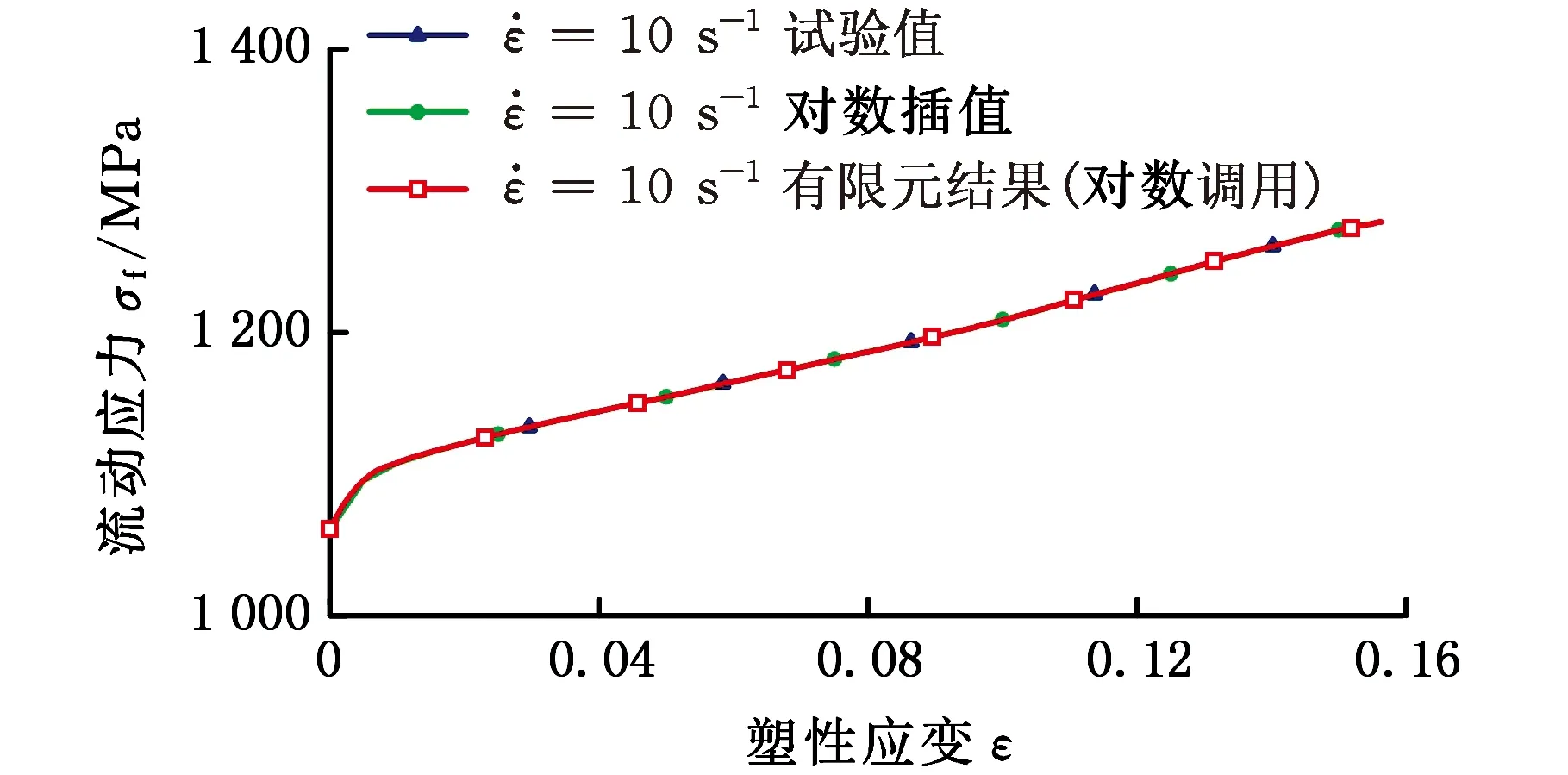
图10 对数插值、有限元仿真与试验结果的比较Fig.10 Comparison of logarithmic interpolation, finite element simulation and testing results
综合图9和图10可知,列表插值法相比J-C和C-S动态本构模型能更好地描述SUS301L-HT不锈钢的动态力学特性。
4 吸能结构特性分析
根据上述研究,SUS301L-HT不锈钢材料的应变率效应对结构的冲击动态响应有显著影响,本节在考虑应变率效应的前提下对结构吸能特性进行了研究。
薄壁管经常被用于列车司机室前端的吸能防爬结构的设计中[22]。以典型薄壁吸能结构为研究对象,对其吸能特性进行研究。有限元模型采用移动刚性板轴向恒速冲击底端与刚性板固接的薄壁圆管,底部刚性板被完全约束。薄壁圆管自身添加自接触,与各刚性板间添加面面接触。圆管直径200 mm,高500 mm,整个有限元模型均采用网格尺寸为1 mm的SHELL单元,如图11所示。
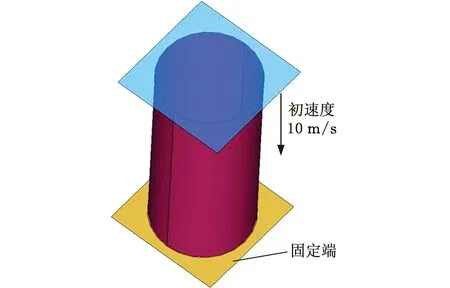
图11 薄壁圆管三维结构Fig.11 3D structure of thin-walled tube
采用两种材料参数:第一种为考虑准静态下SUS301L-HT不锈钢的塑性段载荷曲线,将其记为“参数1”;第二种为采用列表插值法,考虑SUS301L-HT不锈钢在各数量级应变率下的塑性段载荷曲线。两种材料参数分别在25 ms和35 ms时刻的碰撞变形模式见图12。由图12可知,SUS301L-HT不锈钢显著的应变率强化效应使得薄壁管能逐渐形成多个完整的塑性铰,故其变形模式更为稳定。
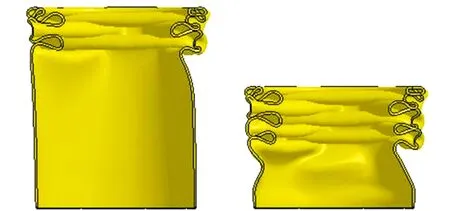
(a)参数1(初始状态) (b)参数1(25 ms碰撞)
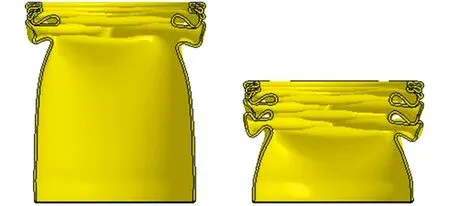
(c)列表插值法(初始状态) (d)列表插值法(35 ms碰撞)图12 薄壁圆管变形模式Fig.12 Deformation modes of thin-walled tube
两种材料参数界面力的对比见图13,可以看出,界面力F随着时间的增加不断振荡降低,但考虑材料应变率效应时,初始峰值力明显增大。
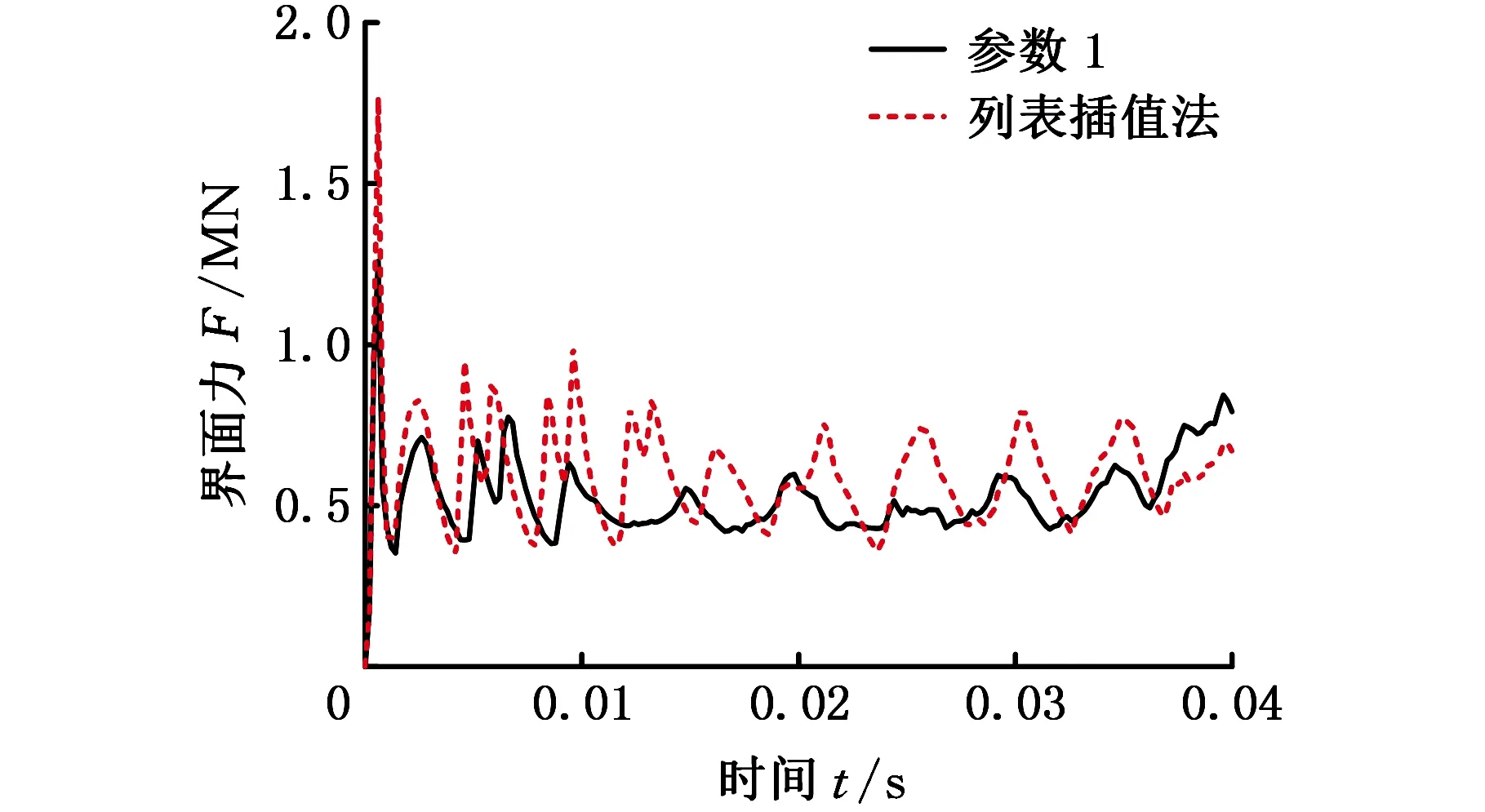
图13 两种材料参数碰撞界面力对比Fig.13 Comparisons of interfacial force of two material parameters
两种材料参数在40 ms内总吸能量E相差了15%,如图14所示。这表明SUS301L-HT不锈钢的应变率效应对薄壁管的吸能量以及变形模式的稳定性有利,但这会使得初始界面峰值力增大,从而导致结构碰撞时的加速度增大,不利于被动安全性。从上述仿真对比的结果来看,薄壁管的动态冲击响应均体现出SUS301L-HT不锈钢的应变率强化效应,这与试验结果一致。在实际设计SUS301L-HT不锈钢吸能结构时,其应变率强化效应对额定吸能容量的设计有利,但必须注意控制其初始峰值力。
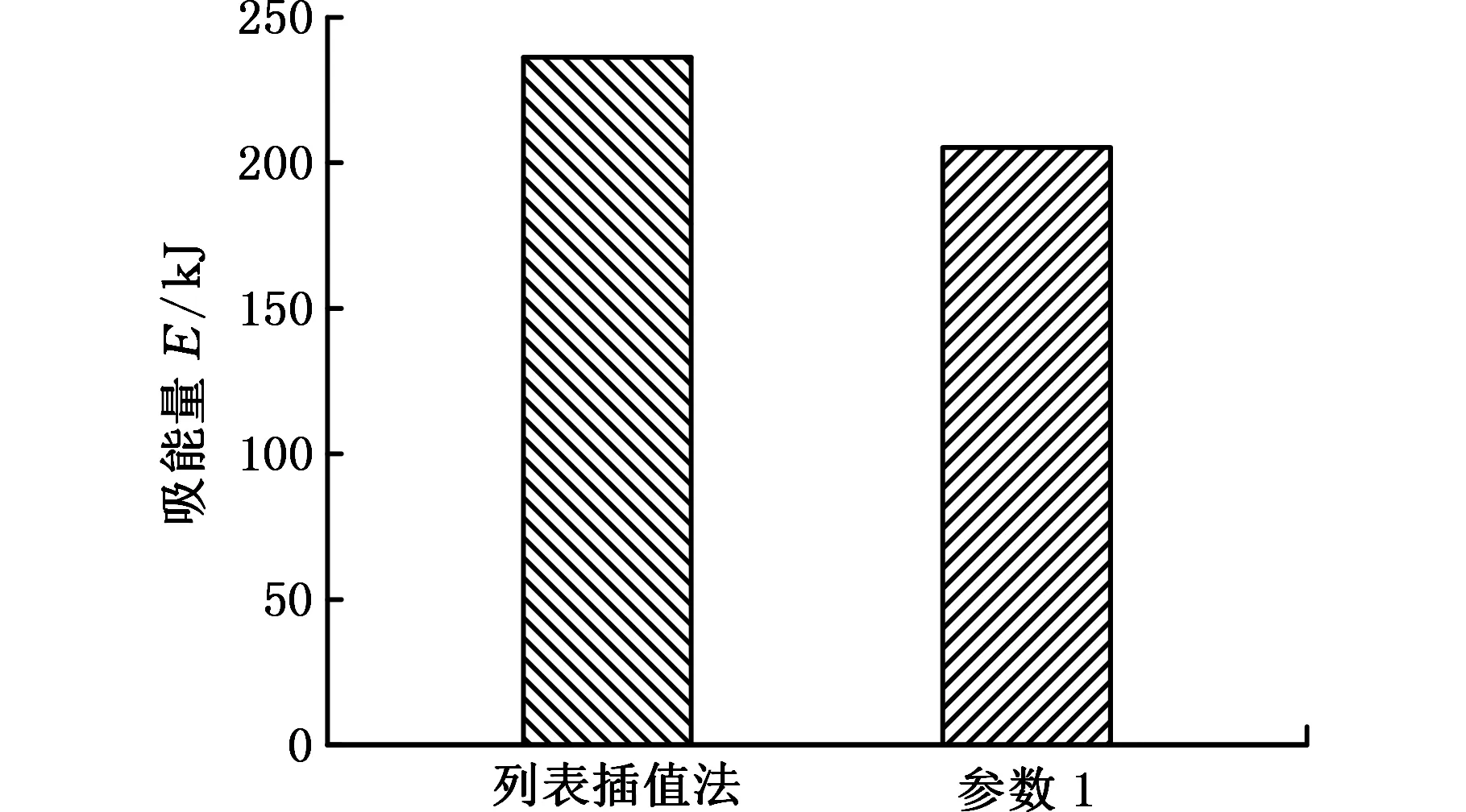
图14 两种材料参数总吸能量对比Fig.14 Comparisons of energy absorption of two material parameters
5 结论
(1)在中低应变率(0.1~500 s-1)情况下,SUS301L-HT不锈钢材料在动态拉伸试验中的应力-应变曲线都比准静态的应力-应变曲线高,表现出明显的应变率强化效应。
(2)中低应变率下的动态拉伸试验中,SUS301L-HT不锈钢材料的动态应力-应变曲线和准静态的应力-应变曲线相交呈明显闭口形态。随着应变率的增大,材料的塑性硬化能力在逐渐降低。该不锈钢材料在中低应变率下存在明显的温度软化特性。
(3)列表插值法能更好地描述SUS301L-HT不锈钢的动态力学性能,且采用列表对数插值法能显著提高该材料插值结果的精度,但会导致数值仿真的计算时间增加。
(4)在中低速碰撞时,考虑应变率效应的SUS301L-HT不锈钢吸能结构的实际吸能量要高于不考虑应变率效应的相同结构的吸能量,且吸能结构的变形模式也更加稳定,但碰撞界面初始峰值力也相对较大。

