非线性几何框架模型在电动汽车车身正向设计中的应用

郭 威 陈吉清 黄佳楠 兰凤崇

1.华南理工大学机械与汽车工程学院，广州，5106402.华南理工大学广东省汽车工程重点实验室，广州，510640

0 引言

近年来中国汽车产业发展迅速，自主品牌正在追赶国外先进水平，基于用户需求和研发人员设计需要的汽车车身正向设计(以下简称“正向设计”)已成为未来发展的必然趋势。伴随汽车电池、电机、电控技术等研究方面的进展与突破[1-4]，电动汽车正成为当今汽车行业的研究热点,电动汽车车身的正向设计也日益得到了汽车开发厂家的重视，并逐渐取代了发展初期的逆向设计。

电动汽车与传统汽车的正向设计流程均分为概念设计、详细设计、样车试制与试验四个阶段[5]。其中，概念设计阶段的任务是在给定造型设计下，从多种结构方案中确定合理的车身结构布置，考虑主要构件断面的特性参数并进行简化模型的快速建模分析，概念设计可提前预测后期设计车身整体性能上的偏差[6]。概念设计阶段结束时就能确定约70%的整车设计成本[7]，从而侧面反映出概念设计阶段在正向设计流程中的重要性。

目前，国内外概念简化模型的构建主要分为两类[8-14]：一是未考虑接头形式的基于梁、壳、质量、弹簧单元组合的简化模型，如ANDERSON[14]已成功为Volvo公司的S40、V50和C70系列轿车搭建了基于梁单元和质量单元的概念简化模型；二是考虑接头形式的基于梁、壳、质量、弹簧单元组合的简化模型。在实际过程中，第一种方式得到了更为广泛的应用。但以往由梁单元、壳单元组合的概念简化模型通常采用线性几何模型及简单矩形梁截面单元的形式，该方式会降低概念简化模型的精度，不能较好地反映详细设计阶段实际复杂的梁截面信息，缺乏后期优化指导意义。

本文在传统汽车正向设计方法的基础上，考虑电动汽车与传统汽车的差别，提出了新的电动汽车车身正向设计开发流程；利用HYPERMESH软件快速建模和自动划分网格的功能，在确定的造型约束及车身结构布置方案下，提出了一种采用非线性几何框架及复杂梁截面单元来逼近车身造型及布置的概念简化模型构建新方法；参考文献[8-14]，提出了概念简化模型的合理性评估依据，利用该评估依据可判断出概念设计阶段是否发挥了提前预测整车性能的作用；基于新的电动汽车车身正向设计开发流程，将所提方法应用于一款小型电动汽车的正向开发与实践。

1 概念设计阶段模型构建与CAE性能分析预测

新的电动汽车车身正向设计开发流程见图1，只有概念简化模型符合整体设计性能要求时才能进入下一步详细设计阶段，因此第一步的工作是构建概念简化模型。在概念设计阶段采用未考虑接头形式的基于梁、壳、质量、弹簧单元组合的简化模型，搭建由梁单元、壳单元组合而成的概念简化模型，并对概念设计阶段的计算机辅助工程(computer aided engineering，CAE)性能进行分析与预测。

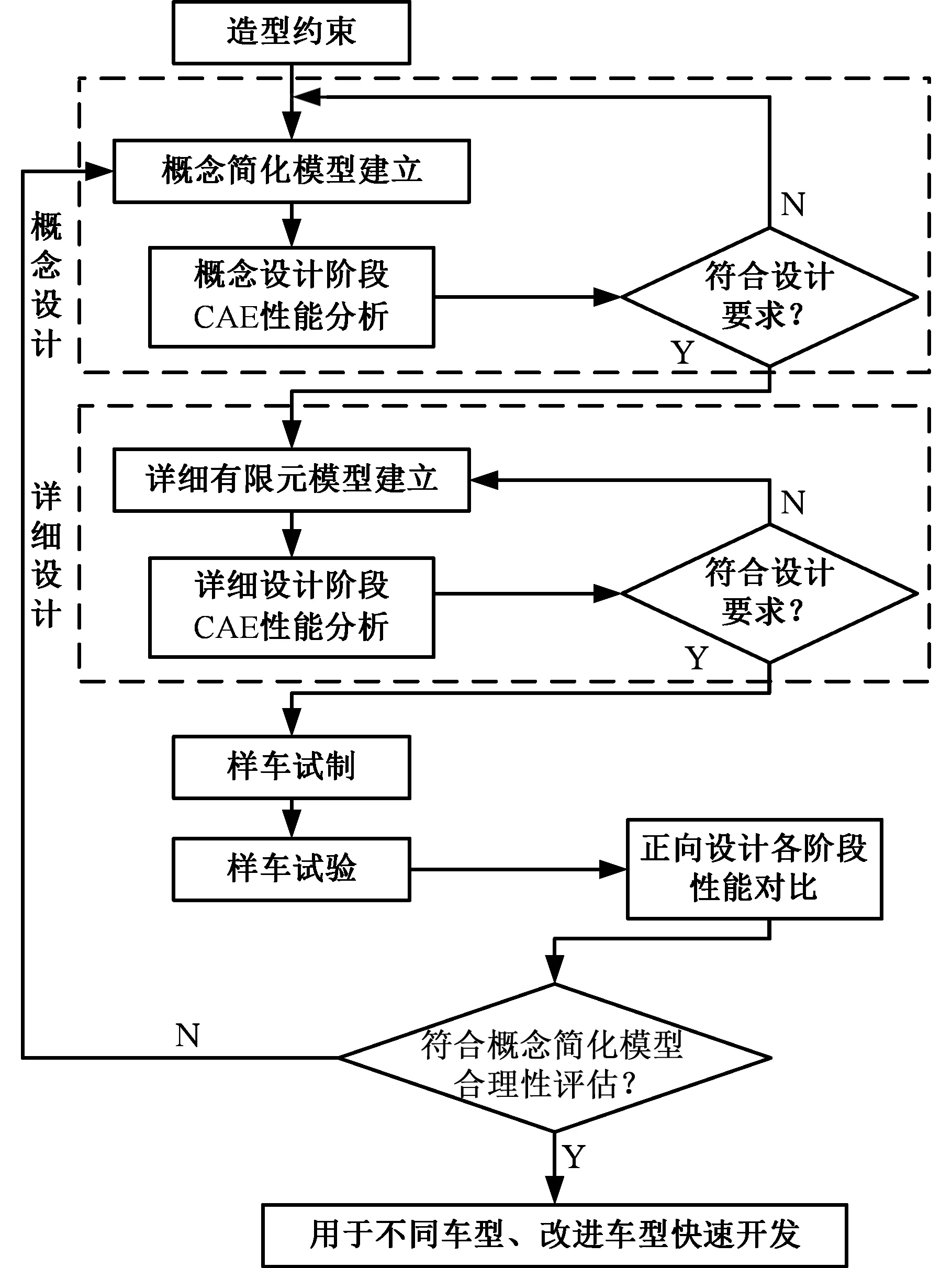
图1 电动汽车车身正向设计流程Fig.1 The forward design process of the electric vehicle body

1.1 非线性几何框架的建立

首先在HYPERMESH中导入造型面，将已确定的车身结构布置方案抽象简化为梁结构和板结构。建立反映梁结构的主要特征点时，在曲率变化大的位置可创建多个点，采用曲线方式进行连接并拟合。对于复杂的梁结构，如A、B柱，采用内外多段式来划分，原因是考虑A、B柱梁结构截面变化较大，采用多段拟合能更加贴合后期详细设计。将所有梁结构在HYPERMESH中用线框结构来简化，而板结构可采用HYPERMESH及CATIA软件混合建模的方式，相对简单的板件(如地板)可直接在HYPERMESH中建立，而车顶板、前轮罩在CATIA中建模。根据上述方法搭建的电动汽车白车身的非线性几何框架模型如图2所示。

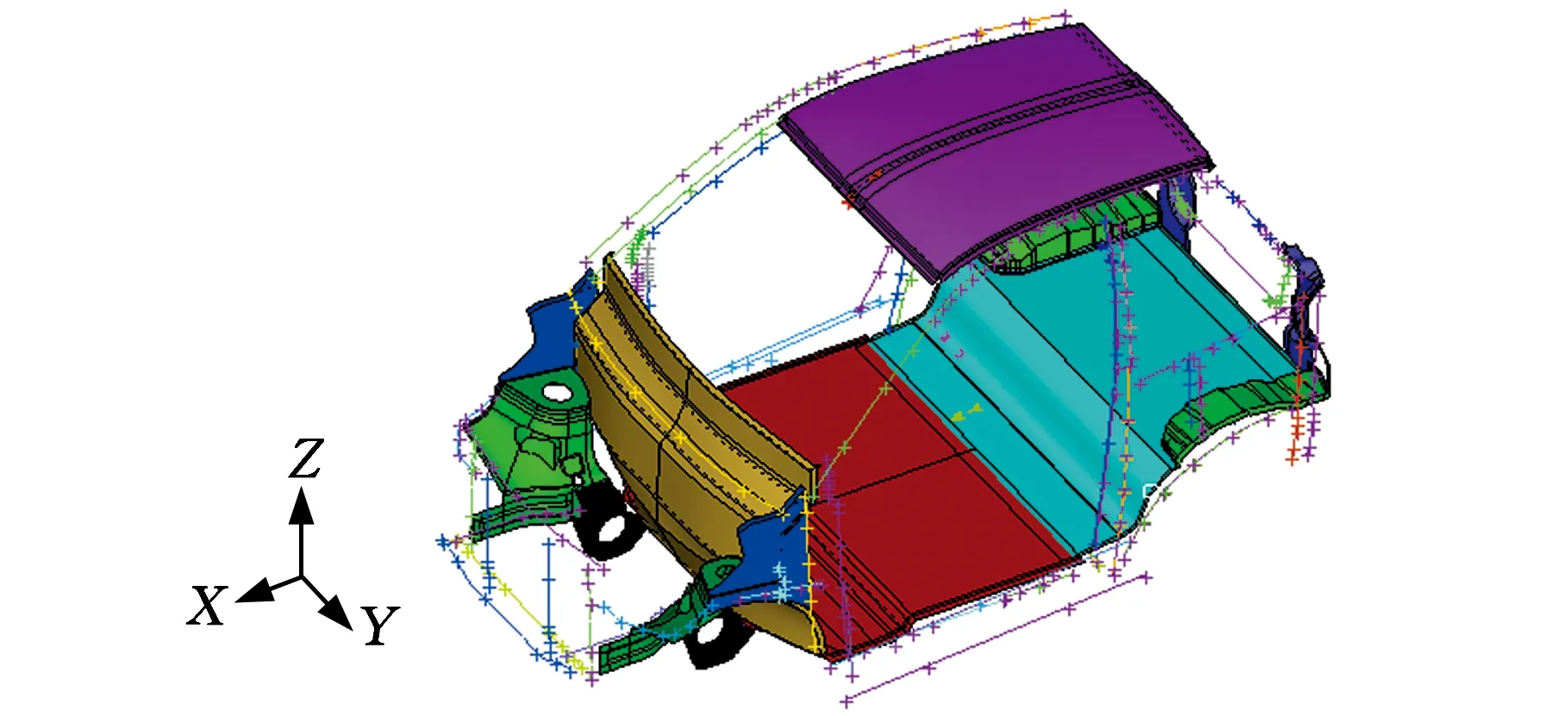
图2 白车身非线性几何框架模型Fig.2 Nonlinear geometric frame model of body-in-white

1.2 梁截面数据库的建立

梁单元具有承受轴向力、剪切力、弯扭矩的特性，通常用于概念简化模型中替代后期详细设计中的壳单元。梁单元的截面参数是其最重要的特征属性，反映了结构对各向载荷下的力学性能。

在分析以往概念简化模型梁截面形式及现实车辆中常见车身结构断面的基础上，在HYPERBEAM中建立了40多种不同类型的梁截面数据库，为后期详细设计阶段的梁截面选型提供了不同可能的组合方案。因篇幅有限，表1仅展示了梁截面数据库中建立的几个关键部位的截面轮廓及其性能参数，其中IY、IZ、IYZ分别为截面对Y轴、Z轴、YZ平面的转动惯量。

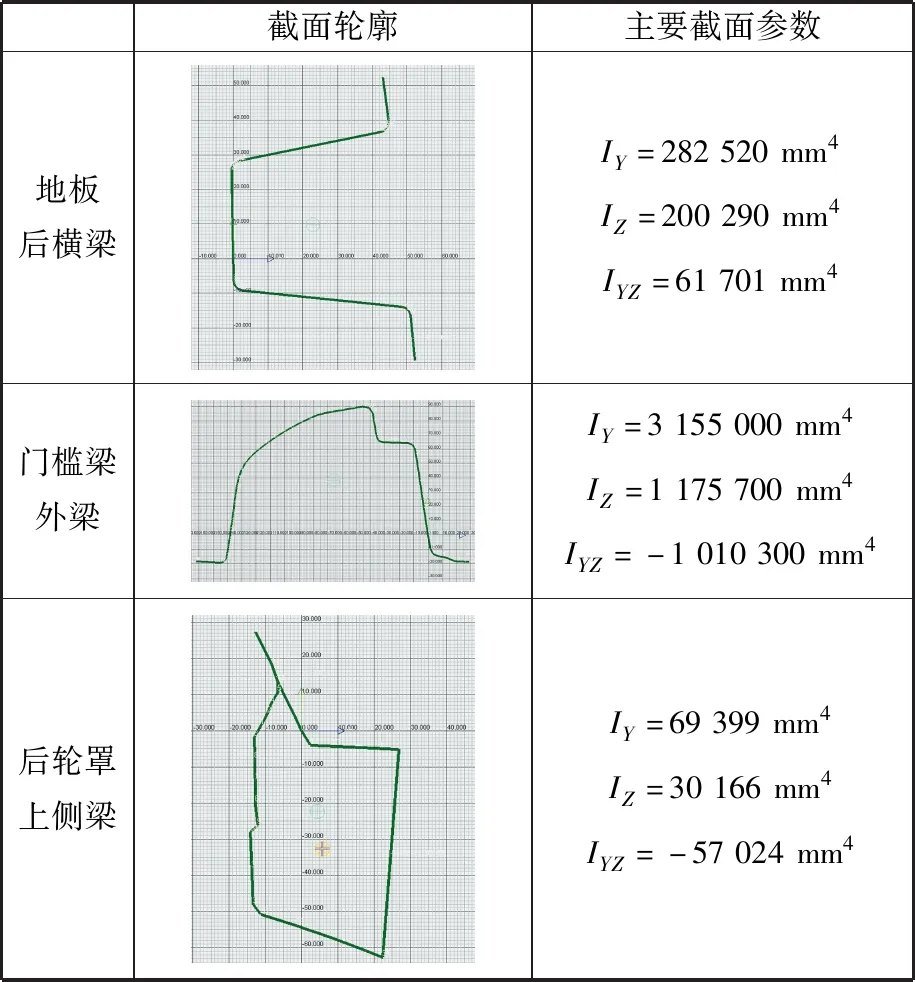
表1 主要梁结构截面轮廓及参数Tab.1 Profile and parameters of the main beam structure

1.3 基于复杂梁截面的概念简化模型的建立

从以往概念简化模型的研究分析中可以发现，概念设计阶段简化模型的构建方法是影响概念简化模型精度的一个重要因素。分析文献[8-14]发现，在构建概念简化模型时针对梁单元的建立均无相对完整的方法论述。基于梁单元应反映实际车身梁结构空间方向这一核心理念，本文提出了一种基于复杂梁截面的梁单元建立原则与流程方法，如图3所示。

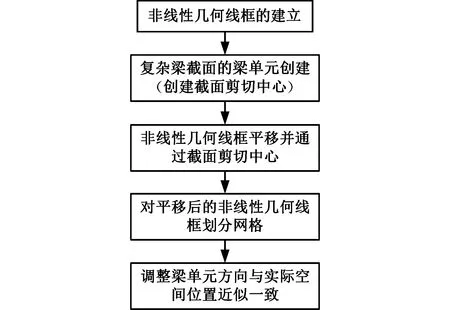
图3 梁单元的建立流程Fig.3 Establishing process of beam element

基于复杂梁截面的梁单元建立原则就是找到梁截面的剪切中心，平移对应几何线框使其通过截面剪切中心，对调整后的非线性几何框架赋予梁单元截面属性，并调整梁截面局部坐标系中的Y轴方向，使其与实际车身结构在空间坐标系下的位置方向近似一致。

图4a中的曲线为右侧A柱梁截面轮廓，曲线外的圆点为截面剪切中心。图4b中的1号线为原非线性几何线框，2号线为1号线平移后通过剪切中心的非线性线框。具体操作如下：对2号线进行梁单元网格划分，调整截面局部坐标系下的Y轴在空间坐标系下的指向，使梁单元方向与实际车身结构在空间位置上近似一致，如图5所示。完成所有梁单元划分之后，对剩下的板状结构划分2D壳单元网格。在建立单元连接问题上，因侧重点不同，故仅采取了以下原则：不同梁单元之间，以及梁单元与壳单元之间的连接均采用刚性连接方式来模拟；刚性连接的连接间距可比后期详细设计阶段中的焊点连接间距稍大，以减小因刚性连接而导致的结构刚度偏大。

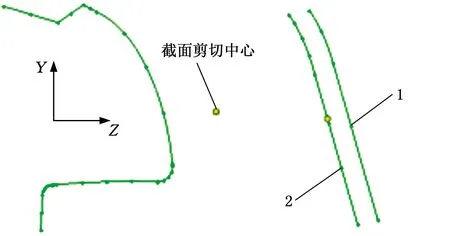
(a)创建剪切中心 (b)平移几何线框图4 非线性几何线框平移Fig.4 The translation of nonlinear geometric line frame

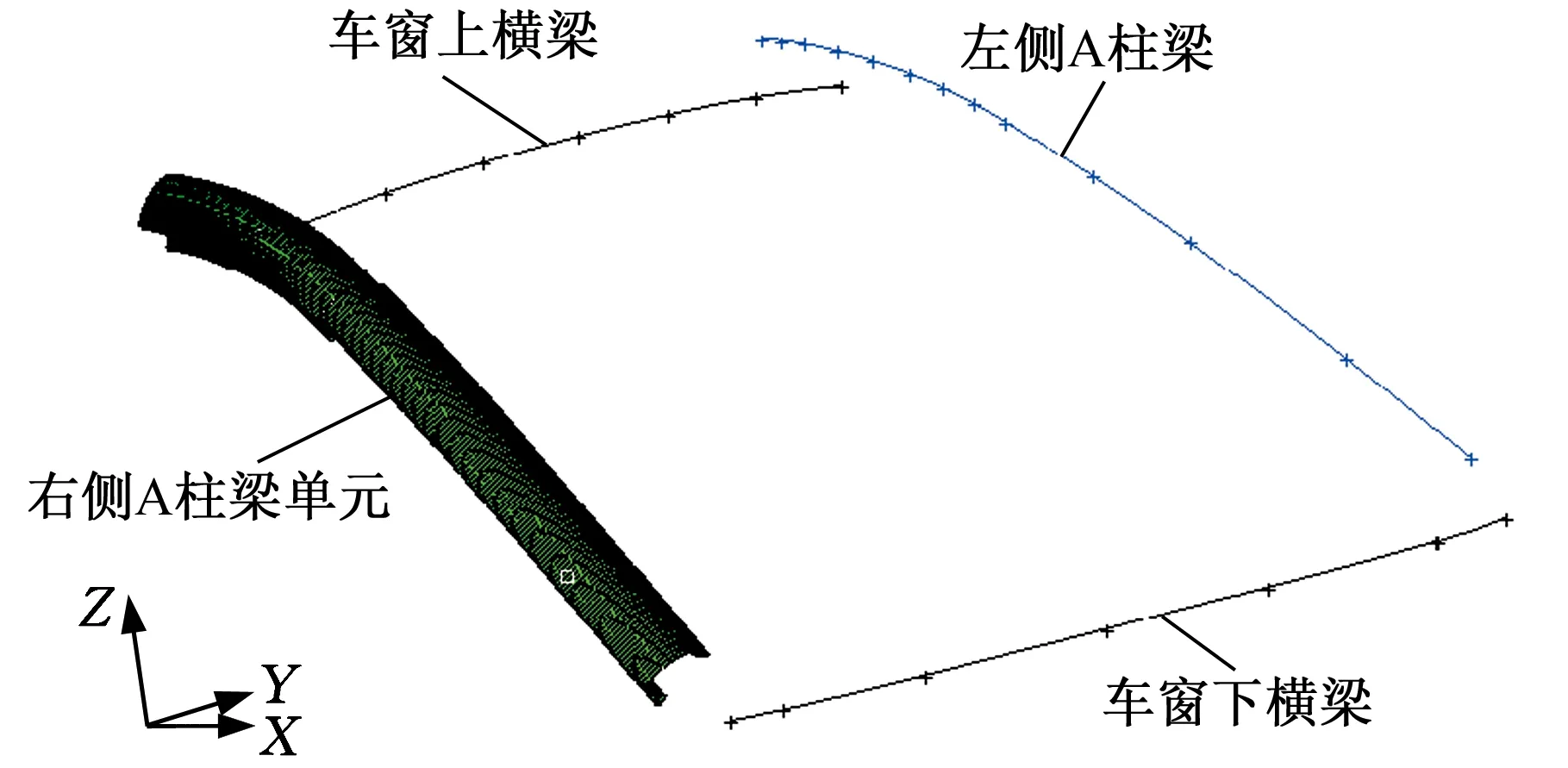
图5 划分梁单元Fig.5 Beam element mesh

基于复杂梁截面的概念简化模型如图6所示。从3D显示方式(图6b)来看，概念设计阶段构建的简化模型在车身结构上整体符合设计要求，可进入下一步分析。

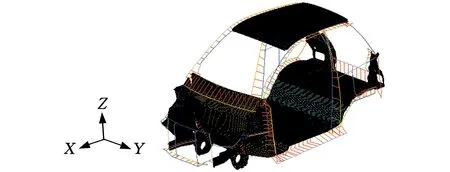
(a)2D显示方式

(b)3D显示方式图6 概念简化模型的建立Fig.6 The establishment of conceptual simplified model

1.4 概念设计阶段CAE性能分析与预测

1.4.1弯曲刚度仿真分析

分别约束前悬架左右安装点Y、Z方向和Z方向的自由度，分别约束后悬架左右安装点X、Y、Z方向和X、Z方向的自由度。加载位置选取在左右两侧门槛梁与座椅平行的位置，左右加载力的大小均为1 kN，共2 kN。选取加载点位置作为测量点。弯曲刚度的计算表达式如下：

(1)

式中，F为加载力；d为测量点位移；u1、u2分别为左测点和右测点的输出位移。

利用HYPERMESH软件中的RADIOSS求解器对弯曲工况进行求解，得到概念简化模型在弯曲工况下的位移云图，见图7。由分析结果可知，左右两侧加载点的输出位移分别为0.116 7 mm和0.119 9 mm，由式(1)计算得到概念简化模型的弯曲刚度为16 906.17 N/mm。

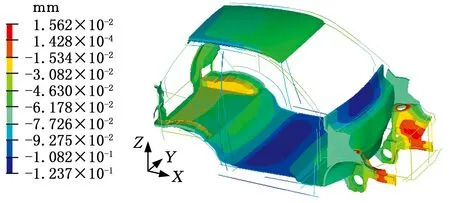
图7 概念简化模型弯曲工况位移云图Fig.7 The displacement contour of conceptual simplified model under bending condition

1.4.2扭转刚度仿真分析

约束后悬架左右安装点各自6个方向(即X、Y、Z移动及旋转方向)的自由度。在前悬架左右安装点分别施加Z轴正向力2 kN和Z轴负向力2 kN。位移测点分别选取左右前悬架与车身的固定连接处。扭转刚度的计算表达式如下：

(2)

式中，M为扭矩， N·m；θ为倾斜角度，(°)；L为左右前悬架固定点间距，通过测量得到L=1 021.47 mm。

概念简化模型在扭转工况下的位移云图见图8。由分析结果可知，左右两侧加载点的输出位移分别为1.010 mm和1.056 mm，由式(2)计算得到概念简化模型扭转刚度为17 629.79 N·m/(°)。

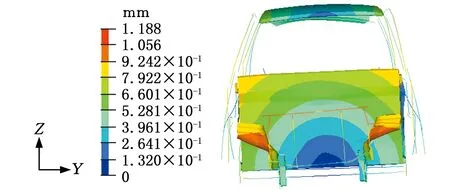
图8 概念简化模型扭转工况位移云图Fig.8 The displacement contour of conceptual simplified model under torsion condition

1.4.3模态仿真分析

模态分析是结构动力分析的基础，常被用来分析结构的振动特性。模态分析的方法又分为理论模态分析和实验模态分析，而在概念开发阶段仅能对理论模态进行分析。理论模态分析通常采用有限元法对振动结构进行离散，建立起由质量矩阵、刚度矩阵、阻尼矩阵组成的系统特征方程，再根据已知边界条件对上述特征方程进行求解，从而得出系统不同频率下的振动特性[15]。

同样利用HYPERMESH软件中的RADIOSS求解器对概念简化模型进行理论模态求解。前四阶振型的位移云图见图9，概念简化模型前四阶的固有频率见表2。

根据上述CAE性能分析结果以及开发此款小型电动汽车时团队设定的目标(即弯曲刚度大于10 000 N/mm、扭转刚度大于10 000 N·m/(°)、一阶固有频率高于25 Hz)可以判断，由概念设计阶段简化模型预测得到的整车性能均能完全满足该小型电动汽车的设定目标，因此可对电动汽车进行下一步详细设计。

2 详细设计阶段模型建立与CAE性能分析

2.1 详细设计阶段有限元模型的建立

详细设计阶段的具体主要任务是对车身零部件进行连接方案、密封性、形貌优化、参数优化等设计，其中包括接头设计、加强筋和减重孔设计，以及优化钣金件的厚度等。基于上述满足要求的概念简化模型，对该款电动汽车进行详细设计，最终得到图10所示的详细设计阶段有限元模型(以下简称“详细有限元模型”)。以前防火墙为例，其概念设计阶段和详细设计阶段的设计分别见图11和图12。

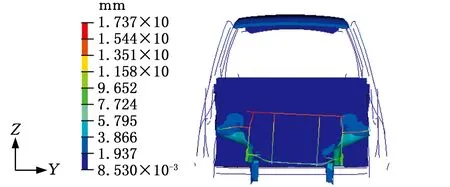
(a)一阶振型

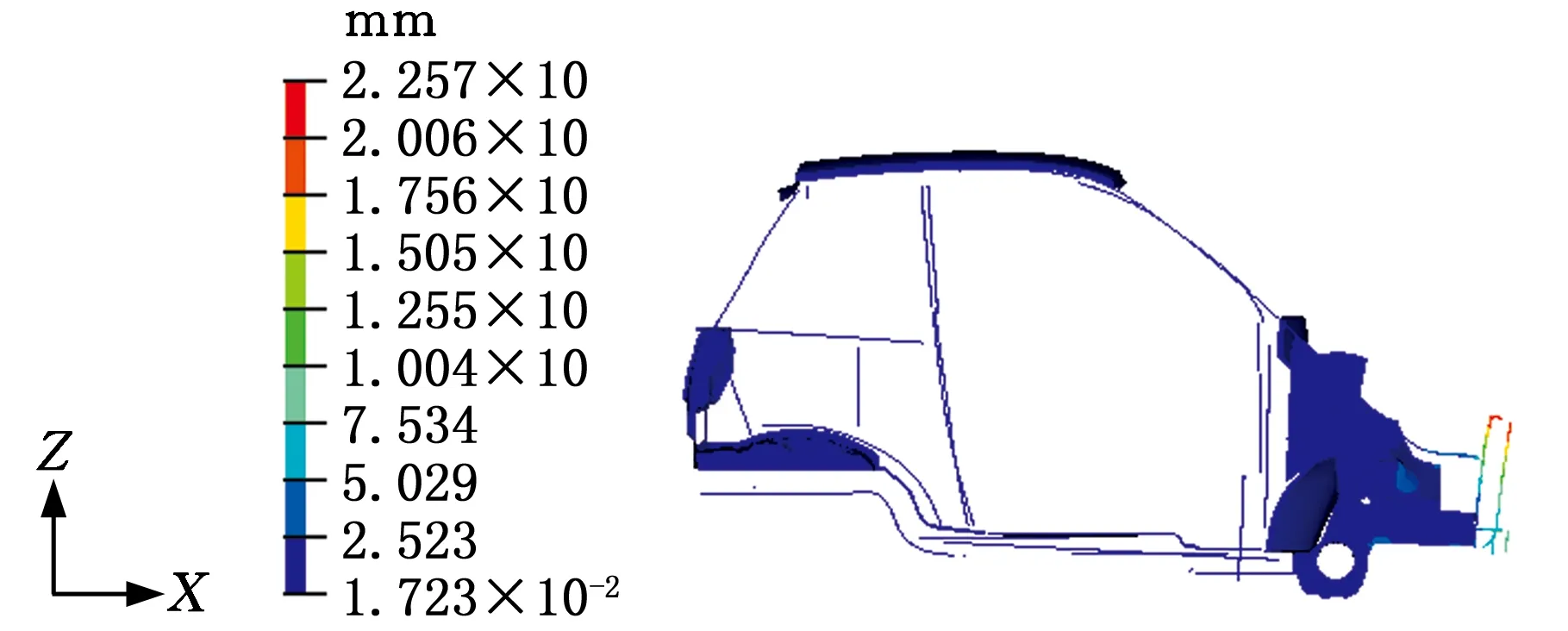
(b)二阶振型

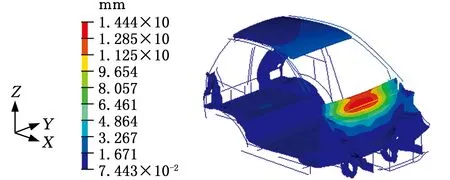
(c)三阶振型

(d)四阶振型图9 概念简化模型前四阶振型Fig.9 The first four mode shapes of the conceptual simplified model

表2 概念简化模型前四阶频率Tab.2 The first four frequencies of the conceptual simplified model

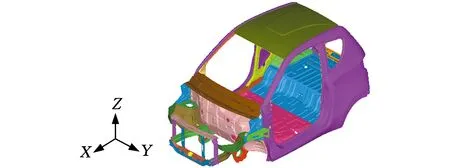
图10 详细设计阶段有限元模型Fig.10 The finite element model of the detailed design phase

图11 概念设计阶段的前防火墙设计Fig.11 The front firewall design at the conceptual design stage

图12 详细设计阶段的前防火墙设计Fig.12 The front firewall design at the detailed design stage

2.2 详细设计阶段CAE性能分析

2.2.1弯曲刚度仿真分析

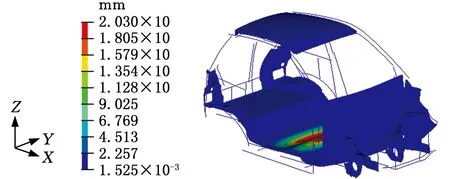
采用与概念简化模型相同的加载方式与约束，得到详细有限元模型在弯曲工况下的位移云图，见图13。由分析结果可知，左右两侧加载点的输出位移分别为0.137 6 mm和0.139 4 mm，由式(1)计算得出详细有限元模型的弯曲刚度为14 440.43 N/mm。

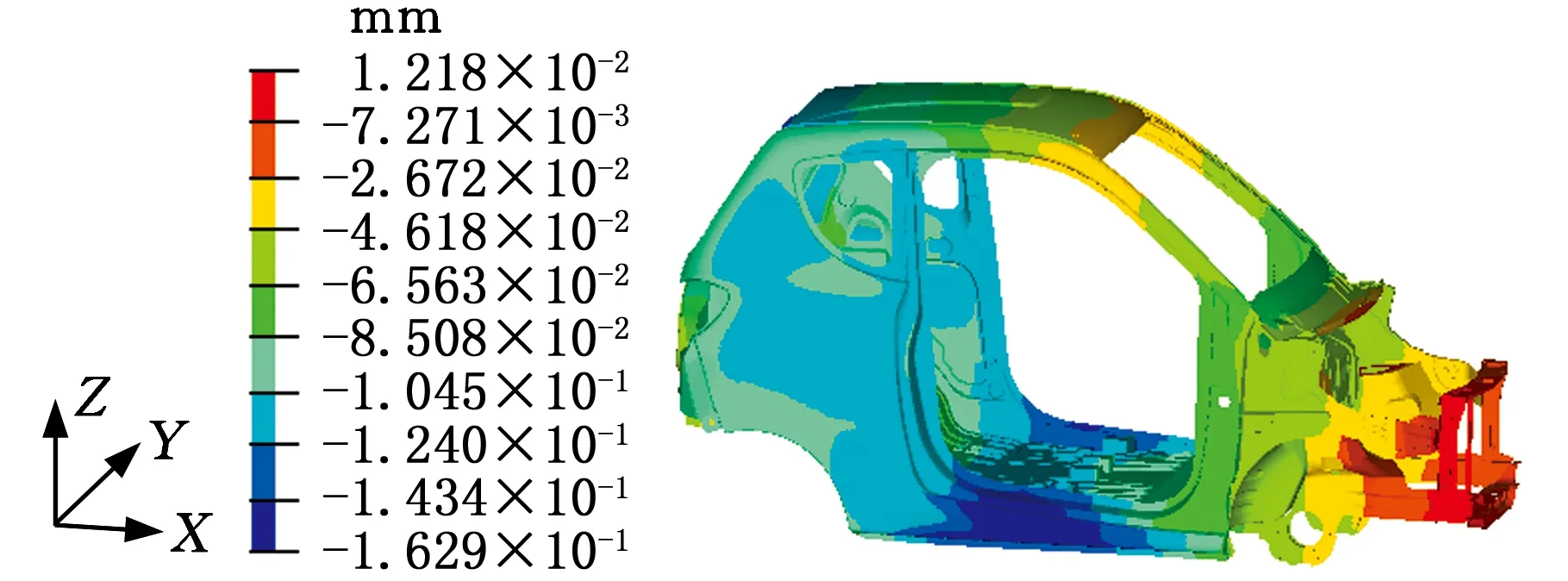
图13 详细有限元模型弯曲工况位移云图Fig.13 The displacement contour of the detailed finite element model under bending condition

2.2.2扭转刚度仿真分析

采用与概念简化模型相同的加载方式与约束，得到详细有限元模型在扭转工况下的位移云图，见图14。由分析结果可知，左右两侧加载点的输出位移分别为1.146 mm和1.303 mm，由式(2)计算得出详细有限元模型的扭转刚度为14 872.89 N·m/(°)。

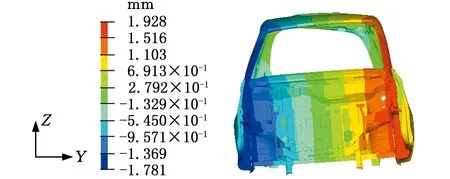
图14 详细有限元模型扭转工况位移云图Fig.14 The displacement contour of the detailed finite element model under torsion condition

2.2.3模态仿真分析

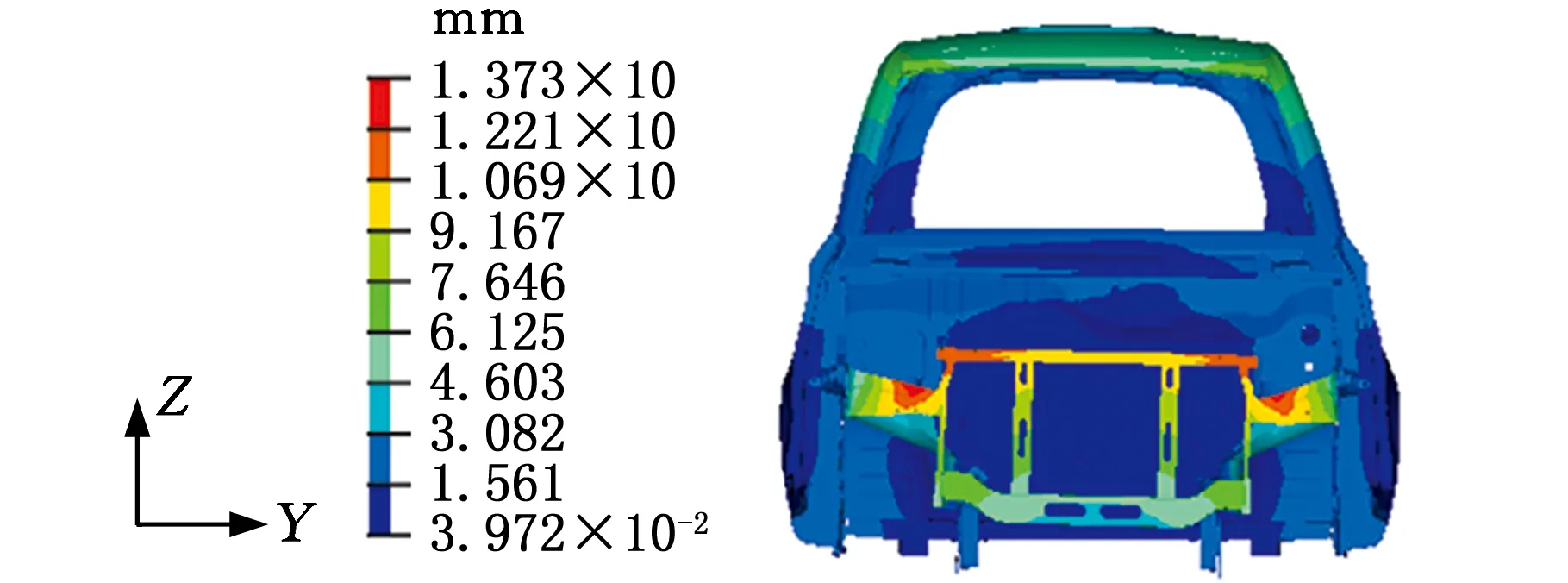
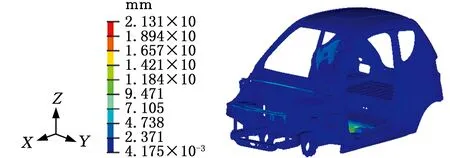
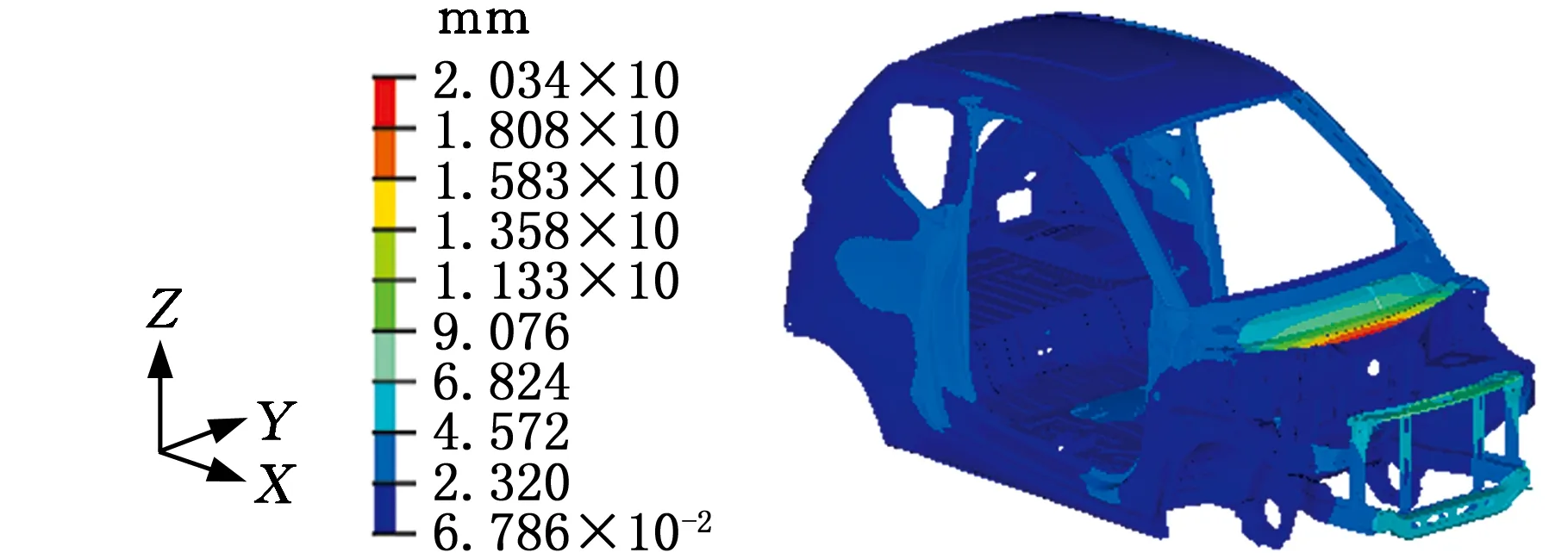
采用与概念简化模型相同的求解方式对详细有限模型进行模态求解，前四阶振型的位移云图见图15，详细有限元模型前四阶的固有频率见表3。

(a)一阶振型

(b)二阶振型

(c)三阶振型

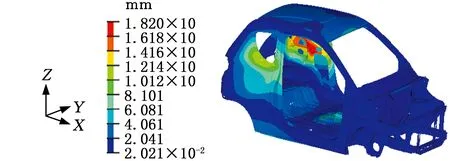
(d)四阶振型图15 详细有限元模型前四阶振型Fig.15 The first four mode shapes of the detailed finite element model

由详细设计阶段的分析结果以及前期开发设定的目标(弯曲刚度大于10 000 N/mm、扭转刚度大于10 000 N·m/(°)、一阶固有频率高于25 Hz)可知，详细设计阶段的有限元模型也满足设计要求，可进一步进行样车试制与试验。

表3 详细有限元模型前四阶频率Tab.3 The first four modes of the detailed finite element model

3 样车模态实验及正向设计各阶段性能对比

3.1 样车模态实验

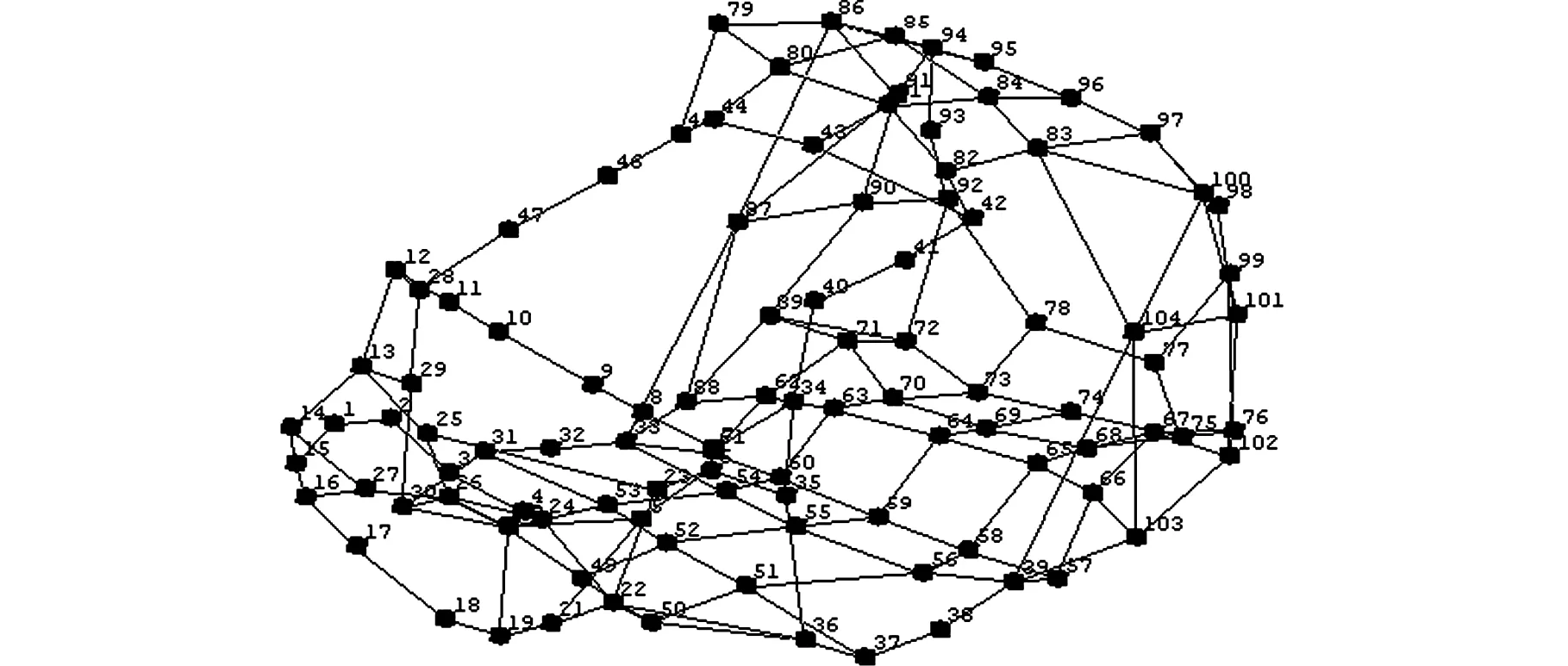
实验方案采用锤击法单点激励输入测单点响应的方式，对生产的样车车身进行自由模态实验，整车共布置104个测点，部分测点分布见图16(如编号4为其中之一测点)。

图16 白车身实验测点分布Fig.16 Test point distribution of BIW

实验模态前四阶振型见图17。实验模态前四阶频率值见表4。

3.2 正向设计各阶段性能对比

为判断概念简化模型的有效性，本文提出了概念简化模型的合理性评估依据：概念简化模型与后期详细有限元模型、样车实验模态的性能指标误差在25%以内，即可认为概念简化模型设计合理。

3.2.1静态性能指标对比

不同阶段的静态性能对比见表5。从表5中可以看出，概念设计阶段简化模型的弯曲刚度比详细设计阶段有限元模型的弯曲刚度大17.1%，概念简化模型的扭转刚度比详细有限有模型的扭转刚度大18.5%，静态性能指标上的误差均在25%以内，可认为概念设计阶段简化模型能较为准确地预测后期详细设计的静态性能。

3.2.2动态性能指标对比

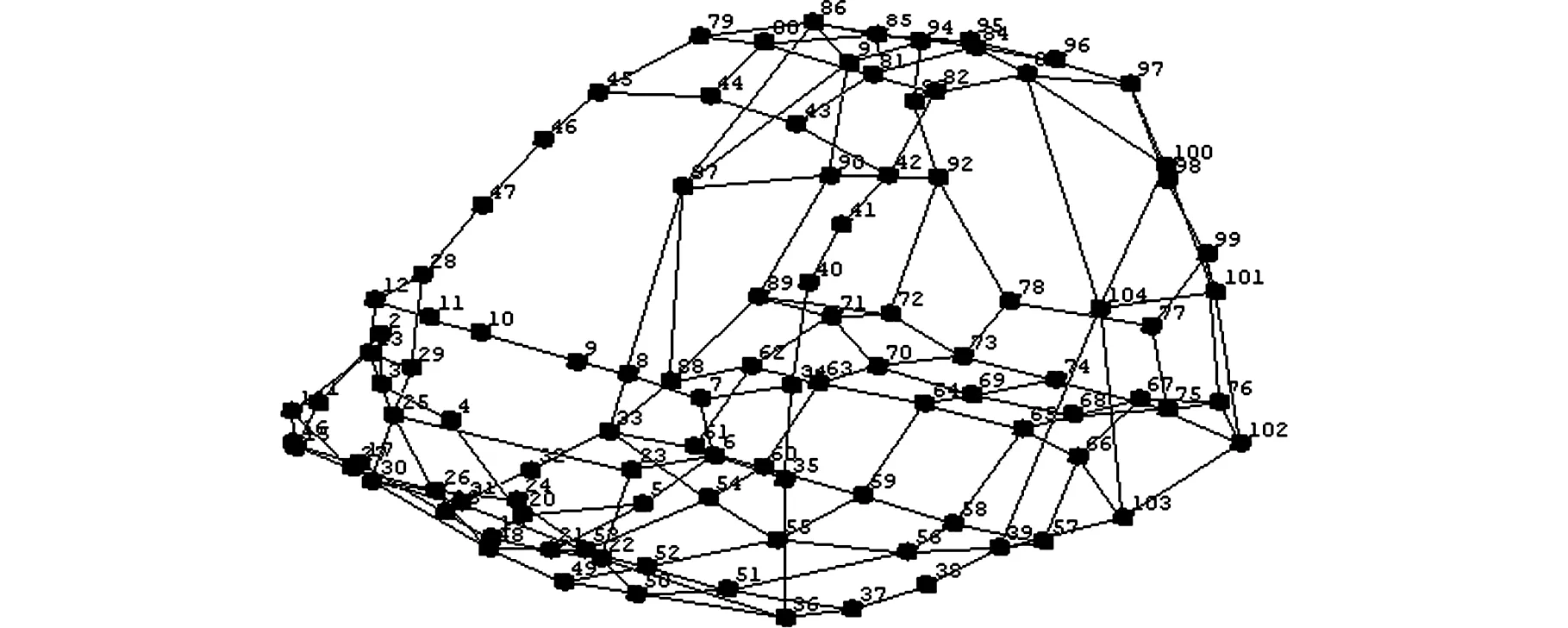
在不同设计阶段的振型方式上，实验模态的一阶振型表现为前散热器支架及车身顶部的扭转；二阶振型为前散热器支架的Z轴翘曲；三阶振型表现为前挡风玻璃下板及前散热器支架的振动；四阶振型表现为后轮罩上板的向外扩张、向内收缩，中部地板的凸起及前散热器支架的微幅振动。从概念简化模型和详细有限元模型的结果来看，两种模型的前三阶振型与实验模态的前三阶振型方式均较为吻合，只是在二阶振型中的详细有限元模型出现了地板的局部模态，前散热器支架与前挡风玻璃仅出现了小幅摆动位移，但其振型与实验模态振型保持一致。在第四阶振型中，由于概念简化模型在后轮罩上板处采用了截面宽厚的梁单元，以致该处的结构刚度大于该处采用薄壳单元的详细有限元模型的刚度，因此只出现了中部地板的凸起和前散热器支架的小幅振动。经放大观察可以发现，后轮罩上板处仍存在向外扩张和向内收缩的趋势，符合实验模态第四阶振型的表现。

(a)一阶振型

(b)二阶振型

(c)三阶振型

(d)四阶振型图17 实验模态前四阶振型Fig.17 The first four mode shapes of the experimental modal

表4 实验模态前四阶频率Tab.4 The first four modes of the experimental modal

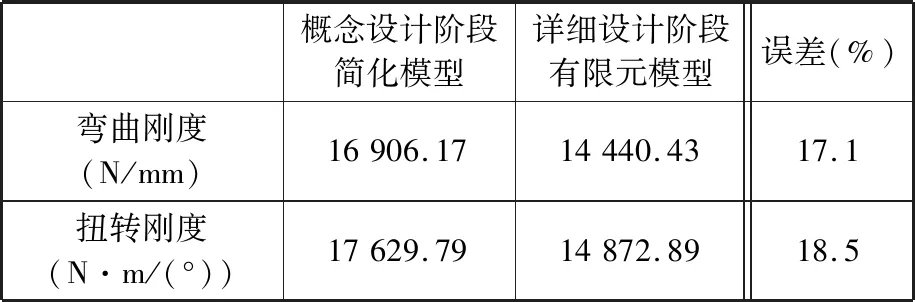
表5 正向设计不同阶段静态性能对比Tab.5 The static performance comparison between different forward design stages

各阶模态频率误差的对比见表6，可以看出，详细有限元模型相对于实验模态的误差均在5%以内，验证了详细有限元模型的有效性；同时概念简化模型相对详细有限元模型和实验模态的平均误差分别为10.9%和15.4%，均小于25%，且处于所提出的评判概念简化模型合理性依据的误差范围内。

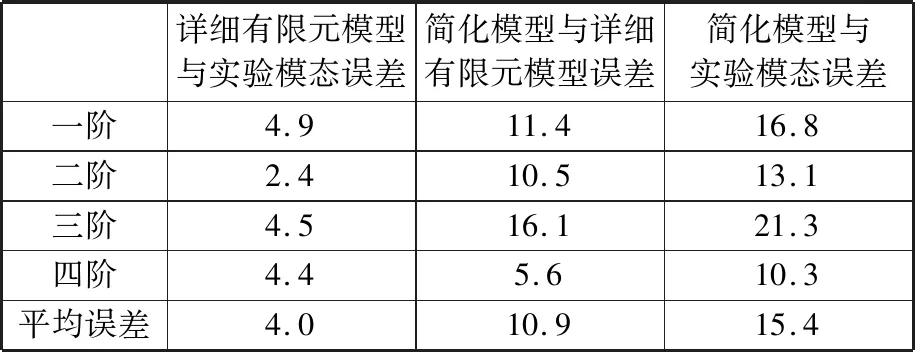
表6 正向设计不同阶段模态频率误差Tab.6 The modal frequency error between different forward design stages %

由上述振型方式和模态频率误差分析可知，概念简化模型能较为准确地预测后期详细设计阶段和样车的模态性能。

4 结论

(1)在汽车车身正向设计的概念设计阶段提出了一种新的、采用非线性几何框架及复杂梁截面单元来逼近车身造型及布置的概念简化模型构建方法以及电动汽车车身正向设计开发流程。

(2)结合一款小型电动车项目开展了电动汽车车身正向设计方法研究与实践。依次完成了电动汽车的概念设计与分析、详细设计与分析、样车试验与分析的工作，并针对概念设计阶段的任务是预测后期设计整车性能的问题，提出了对概念简化模型合理性的评估依据。

(3)所提出的概念简化模型构建方法能较好地反映梁结构在空间的方向和力学性能，可进一步提高概念简化模型的预测精度；对比正向设计各阶段车身性能指标结果，概念简化模型的静/动态性能指标误差均小于25%，处于所提出的评估概念简化模型合理性依据的范围内。

此次电动汽车正向开发与实践体现了应用电动汽车正向设计流程对电动汽车进行正向开发的正确性，为电动汽车不同车型、改进车型的正向设计提供了参考。