2018年全国高中数学联赛一试B卷第11题的探析

(乐从中学，广东 佛山 528315)

1 题目呈现

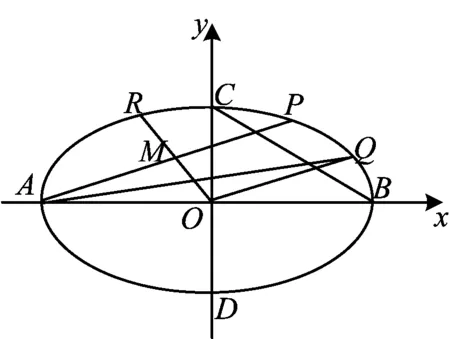
图1

(2018年全国高中数学联赛一试B卷第11题)

本赛题主要考查直线与直线平行、线段的中点、直线的斜率及椭圆等基础知识和运算求解的基本技能，突出考查学生对数量关系进行转化与运算的能力以及推理论证能力.作为解答题中的压轴题，本赛题对考生的思维水平和数学素养有较高的要求.

2 证法探析

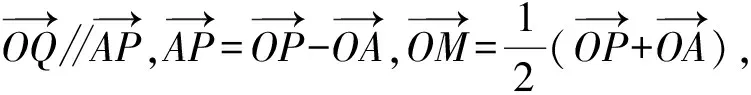
此时点Q,R的坐标可分别表示为(λ(x0+a),λy0),(μ(x0-a),μy0).由于点Q,R都在椭圆上，因此

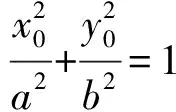
解得

从而|OQ|2+|OR|2=

故线段OQ，OR，BC能构成一个直角三角形.

评注本证法是官方参考答案，利用向量的线性运算,将点Q,R的坐标转化为用椭圆上的点A,P的坐标表示，难点也恰恰在此，同时本证法的代数变形及运算较为繁琐.

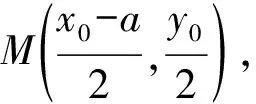
即

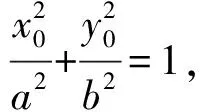
设R(x1,y1)，Q(x2,y2),则

从而

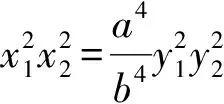
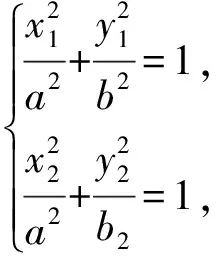
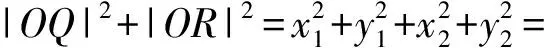
a2+b2=|BC|2,

因此线段OQ，OR，BC能构成一个直角三角形.

设R(acosθ1,bsinθ1)，Q(acosθ2,bsinθ2),从而

于是

tanθ1tanθ2=1，

即

进而|OQ|2+|OR|2=

a2cos2θ1+b2sin2θ1+a2cos2θ2+b2sin2θ2=

(a2-b2)cos2θ1+b2cos2θ1+b2sin2θ1+(a2-

b2)cos2θ2+b2cos2θ2+b2sin2θ2=

2b2+(a2-b2)(cos2θ1+cos2θ2)=

2b2+(a2-b2)=a2+b2=|BC|2,

故线段OQ,OR，BC能构成一个直角三角形.

图2

证法4(平面几何视角)如图2，作⊙O：x2+y2=a2，过点R作RB⊥x轴于点B，交⊙O于点S，过点Q作QA⊥x轴于点A,交⊙O于点T,联结OS,OT.

设R(x1,y1)，Q(x2,y2)，S(x1,y3),T(x2,y4),则

求得

同理可得

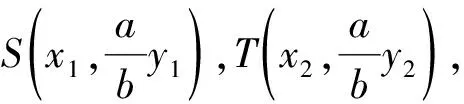
即

OS⊥OT,

于是

∠AOT+∠BOS=90°.

又∠ATO+∠AOT=90°，可得

∠ATO=∠BOS, ∠OAT=∠OBS=90°，OT=SO，

从而

△AOT≌△BSO,

于是

AO=BS,AT=BO,

因此|OQ|2+|OR|2=

|OA|2+|AQ|2+|OB|2+|BR|2=

a2+b2=|BC|2,

故线段OQ，OR，BC能构成一个直角三角形.

评注1)本证法从平面几何的角度思考，借助三角形全等、勾股定理等几何性质，简化了推理和运算过程，具有直观、简捷的特点，方法新颖独到[1].

解析几何是用代数方法研究几何问题，其思路直接明了，平时我们往往注重解析几何的代数运算，轻视其几何推理.实质上解析几何问题的本质是几何问题，它们本身就包含一些重要的几何性质，若能挖掘出题目里蕴含的平面几何元素，充分利用平面几何知识，则可以避开繁琐的代数运算，使解决问题的过程得到简化，方法简洁优美，更好地揭示这些问题的几何性质.因此，解析几何问题应该将解析法与平面几何方法相结合，用充分的思考引领计算，从而得到解决问题的最优方法，这不仅是解决解析几何问题、减少运算量的法宝，还可以更好地提高解题能力[2].

2)本证法的思路来源于教材的例题与习题：

1.如图3，在⊙O:x2+y2=4上任取一点P，过点P作x轴的垂线段PD，点D为垂足.当点P在⊙O上运动时，线段PD的中点M的轨迹是什么？为什么？

(人教A版《数学(选修2-1)》第41页例2)

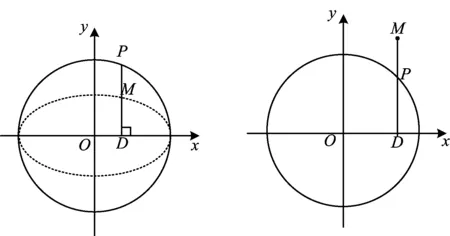
图3 图4

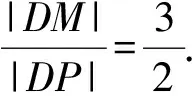
(人教A版《数学(选修2-1)》第50页B组第1题)

从教材的这两个题目，可以得到椭圆与相应的圆之间的联系.

3 背景探析

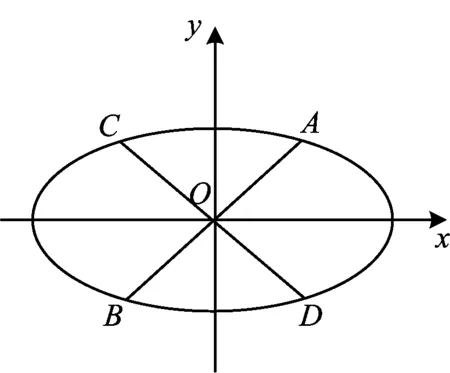
图5

椭圆的共轭直径有很多优美性质，例如：

设AB,CD为椭圆的一对共轭直径，若点A,C的坐标为(x1,y1)，(x2,y2)，则

3)x1y1+x2y2=0；

4) |OA|2+|OC|2=a2+b2；

……

显然，原赛题就是以上述性质2)和性质4)为背景命制的.

4 结束语

从不同的思维角度分析同一道题目，可以得到不同的解题方法.一题多解的方式增加了题目涉及的知识广度，以一带多，减少了考查同样多的知识所需的题量.从数学知识的角度来看，通过解题发现知识之间的相互联系，体会转化过程，从多角度思考和发现问题，构建知识网络体系.这样，在学习基础知识、掌握基本技能的同时，还培养了学生思维的广阔性、深刻性、灵活性以及创新性，让学生对学习的内容有一个整体的认识，并将知识融会贯通，举一反三，开阔眼界，活跃思维，从而提炼出数学思想与方法，这正是数学教学的核心.

数学家波利亚说过：“掌握数学就意味着善于解题.”罗增儒教授说：“数学学习中发生数学的地方都无一例外地充满着数学解题活动.”引导学生学会解题，是数学新课程教学的重要组成部分.同时，数学问题的解决仅仅只是一半，更重要的是解题后的回顾.遇到一道经典试题，需要从多角度、深层次探寻其解法，通法也好，巧法也罢，不仅要比较其优劣，还要清楚其中的方法内涵，知晓其中的来龙去脉，方能实现试题研究价值的最大化.