整合阅读材料的“解三角形的实际应用”教学

(扬州大学，江苏 扬州 225000)

1 教学中应用阅读材料的现状解析

与传统的高中数学教材相比，不同版本的新编高中数学教材中均设有“探索与发现”“阅读与思考”“信息技术应用”等阅读类模块[1]，但一线数学教师普遍对阅读材料的关注度不高.多数教师选择让学生课后自学阅读材料，认为阅读材料是适合学生的课外读物.许多教师认为阅读材料是教材内容的点缀，极少有教师会将其当作正文内容一样对待.笔者认为出现这一现状的根本原因有两个：其一是教师对阅读材料的教育价值认识有限，部分教师无法领会阅读材料的编写意图，忽视了其中所渗透的数学思想，不认同其对学生发展的积极作用；其二是受应试教育观念的影响，多数教师认为阅读材料与高考的关联度较低，不应占用有限的课堂教学时间.

2 阅读材料的教育价值

阅读材料是教材正文内容的拓展和深化，集趣味性、科学性、教育性、知识性于一体.其目的不仅是为了满足不同层次学生的需求，增加教材的弹性，更是为了引导学生体会数学的科学价值和人文精神.阅读材料具有启发性强、针对性强的特点，与学生现阶段所学的知识密切联系，其教育价值是课外读物不可比拟的[2].将数学文化与高考题相结合已成为近年来的必然趋势，而阅读材料正是在教材中渗透数学文化的一种途径和方法.因此，在教学中应重视对阅读材料的分析和探究，从新视角、新情境出发，激发学生的学习兴趣，并在此过程中将数学核心素养的培育深深扎根于教材，避免数学教学的表面化与形式化.

3 教学片段

教学活动1激活旧知.

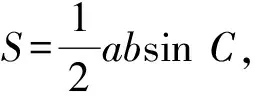
例1某市在进行城市环境建设中，要把一个三角形区域改造成市内公园，经过测量得到这个三角形区域的两边长为68 m，88 m，其夹角为65°，这个区域的面积是多少(精确到0.1 m2)？

设计意图教师先以边、角与面积的关系引导学生思考角与面积是否存在关系，仅知3个角无法确定三角形大小，面积无法仅由角单独确定，从而进一步思考边与面积是否存在关系，层层递进，启发诱导，有助于学生突破思维局限，为后续教学作铺垫.教师通过解决例1这一实际问题，提高学生对解三角形知识的应用意识，培养学生的数学建模、数学抽象和逻辑推理等能力.

教学活动2巩固提升.

事实上，在我国古代，丈量土地时并不能精确测量出两边的夹角，在实际生活中测量三角形的边长更简便.

例2我国宋代著名数学家秦九韶就曾在其著作《数书九章》中以解决土地的实际丈量提出过这样一个问题：“问有沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里，里法三百步，欲知为田几何.”他将三角形的3条边分别称为小斜、中斜和大斜，若一里按五百米计算，则其3条边长分别为6.5 km,7 km,7.5 km，根据题意，如何建立数学模型？如果不作辅助线，你能求解上述问题吗？

根据输入特征图的大小，判断特征图尺寸与输出特征图尺寸的关系，如果输入特征图大于输出特征图大小，则利用可变尺度池化层使得特征图下采样到固定大小的输出，当输入特征图小于固定输出特征图大小时，利用双线性插值，使得网络输出为固定尺寸的特征图。

在学生解决实际问题的基础上，教师进一步提出问题：如果我们将上述问题中三角形的3条边长用更具有一般性的字母a，b，c来代替，是否就能得到三角形边与面积的关系呢？对此，秦九韶曾提出“三斜求积术”，即下述边与面积的关系式：

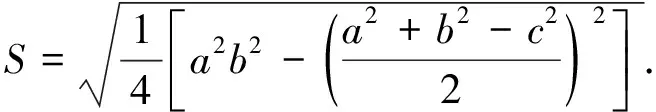
(1)

但历史上他并未给出具体的证明过程，你能运用尽可能多的方法证明该公式吗？

设计意图以《数书九章》中秦九韶所提出的问题创设情境，利用教材中的阅读材料激发学生的学习兴趣，并通过向学生介绍我国数学家秦九韶的生平简介及数学贡献，在拓宽学生视野的同时使其感受数学文化所蕴含的人文精神.教师通过将具体问题抽象化，使学生感受从特殊到一般、从具体到抽象的思想方法.在实际课堂中，多数学生会通过作高的方式运用勾股定理解题，教师可通过提示，引导学生尽可能多地运用所学知识解决问题.在推导秦九韶公式的过程中，通过对三角形面积公式、勾股定理、余弦定理、正弦定理等公式定理的运用，达到对解三角形知识的理解巩固、熟练应用的目的.

教学活动3探索发现.

古希腊数学家海伦也曾提出过三角形边与面积的关系式，该公式最早出现在他的著作《测地术》之中，与秦九韶的“三斜求积术”有异曲同工之妙.若三角形的3条边分别为a，b，c，则其面积为：

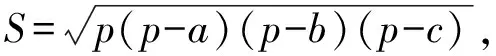
(2)

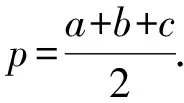
设计意图教师以多媒体呈现不同数学家对海伦公式的不同证明方法，使学生体会多角度看数学问题的思想.通过对比中西方不同数学家对同一问题所得的不同结果，教师可引导学生在体会两式本质等价、形式不同的基础上，感受数学“变中存不变”的美感.

教学活动4应用拓展.

通过刚才的探究，我们发现了三角形边与面积的关系，这样的关系能否推广到四边形中？请同学们以小组合作的方式尝试类比海伦公式求解正方形、矩形、菱形、平行四边形的面积，并猜想四边形边与面积的关系式.由比较、归纳、类比以及猜想，教师引导学生得出下述关系式：

(3)

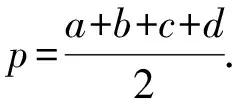
教师引导学生思考并回答下列问题：1)对比式(2)和式(3)，你有怎样的发现？2)对任意的四边形，式(3)都成立吗？3)你能归纳出对于怎样的四边形其边与面积具有上述关系？4)我们可以将有这样特征的四边形称为“海伦四边形”，我们还在哪里遇到过“海伦四边形”？

(2010年江苏省数学高考试题第14题)

1)根据题意，如何建立数学模型？

2)你认为应该运用哪些知识求解，请尽可能多地给出不同解法，并说说你认为哪种方法更为简便.

设计意图在实际教学中，将结论推广延伸，有利于培养学生的发散思维和创新能力.在对海伦公式的推广研究活动中，教师通过引导学生以合作交流的方式，运用猜想、比较、归纳等数学思想方法，提升其数学分析和直观想像等能力，并使其感受发现问题、分析问题和解决问题的过程.从特殊四边形猜想一般结果，再推广到对任意四边形的思考，这是由易到难的过程，符合学生从特殊到一般的认知规律.最后引导学生归纳总结，并提出“海伦四边形”这一新的定义，同时结合实际问题，在求解过程中使学生体会解三角形的本质.

4 教学思考

本节课是在应用解三角形知识的基础上，结合阅读材料引导学生探究和推广海伦—秦九韶公式.在教学过程中，引导学生体会解三角形知识的实际运用，在对正文内容加以巩固与深化、拓宽学生视野的基础上，渗透从特殊到一般、运算变形、类比猜想、一题多解等数学思想方法，潜移默化地发挥数学文化的显性和隐形价值，进一步提升学生直观想象、数学分析、逻辑推理等方面的数学核心素养.

《普通高中数学课程标准(2017年版)》明确指出：在教学中，要注重数学的产生和发展的历史，使学生了解我国及世界各国的数学成就，同时体会数学在日常生活、科学技术及社会生产中的广泛应用[3].在实施过程中，教师应当增强自身的文化素质，转变教学观念，结合教学内容有意识地将阅读材料融入到教学实践中，并善于挖掘其中蕴含的文化价值.教师应不断加强自身数学修养，才能更好地运用阅读材料的价值，从而提高课堂质量，促使师生共同进步.