立足精准教学 落实核心素养

(金陵高级中学,浙江 长兴 313100)(湖州教育研究中心,浙江 湖州 313000)

2019年3月25日，笔者有幸参加了“浙江省湖州市高中数学优质课”比赛.本文是此次优质课教学设计和课堂教学过程中的点滴感悟，现与大家分享，望同行和专家批评指正.

1 教学分析

1.1 教材分析

本节课是普通高中课程标准实验教科书《数学(必修5)》中第一章“解三角形”第一节内容.学生在初中阶段已经学习了解直角三角形的有关内容以及锐角三角函数等知识，在高中阶段又学习了三角函数、平面向量等相关知识.因此联想所学知识可以启发学生对三角形边角关系作量化探究，发现并证明正弦定理，或者通过初中平面解析几何知识利用外接圆推导正弦定理，也可以利用平面向量数量积等相关知识推导正弦定理.这部分内容是用代数方法解决几何问题的典型代表之一，应用非常广泛.

1.2 学情分析

学生在初中阶段已学过有关三角形的一些知识：

1)勾股定理：a2+b2=c2；

3)A+B+C=π；

4)大边对大角，小边对小角；

5)两边之和大于第三边，两边之差小于第三边.

学生在高中阶段已学过任意角三角函数与平面向量等知识.

1.3 课前疑虑

困惑1本节的重点是证明正弦定理，证明方法非常多，那么选定什么方法进行证明，如何在多种证明方法中取舍呢？

解决方法根据《浙江省普通高中学科指导意见》，结合教材及学情，为了更好地让学生掌握正弦定理的推导过程，笔者最终选定从特殊到一般的证明方法，即：先从直角三角形中发现正弦定理的等比式，经计算机数据分析、猜想验证，最后通过探究讨论证明得到正弦定理，充分体现学生的主体性.

对于其他方法，本节课不能一一探究，但又不能只字不提.本节课采用了“设置课后反思并通过学案进行引导”的方式加以解决.

困惑2本节课的难点是已知两边及其中一边对角解三角形时如何判断三角形解的个数问题，采用哪种方式能让学生清晰、透彻地理解并迅速掌握？

解决方法本节课采用了从实际中来到实际中去的方式，让学生充分认识三角形解的个数产生的原因和判断三角形解的个数的具体措施.

1.4 教学目标

1)掌握正弦定理的推导和证明方法；

2)会运用正弦定理及三角形有关知识，解斜三角形的两类基本问题；

3)引导学生通过观察、推导、比较，由特殊到一般归纳出正弦定理，并进行定理基本应用的实践操作；

4)培养学生在方程思想指导下解三角形问题的能力，通过三角函数、正弦定理等知识间的联系来体现事物之间的普遍联系与辩证统一.

1.5 学科素养

数学抽象：从实际问题中抽象出数学问题，在任意三角形中抽象出正弦定理的一般形式；

逻辑推理：正弦定理的推导与证明；

数学运算：运用正弦定理解三角形；

直观想象：通过数形结合得到判断解的个数问题的一般结论；

数学建模：能够将实际问题转化为解三角形问题；

数据分析：通过数据分析验证正弦定理,判断三角形解的个数.

1.6 教学重点

正弦定理的探索和证明及其基本应用.

1.7 教学难点

已知两边和其中一边的对角解三角形时，解的个数的讨论.

2 教学实录

2.1 情境导入

问题1我们只要求出什么即可？

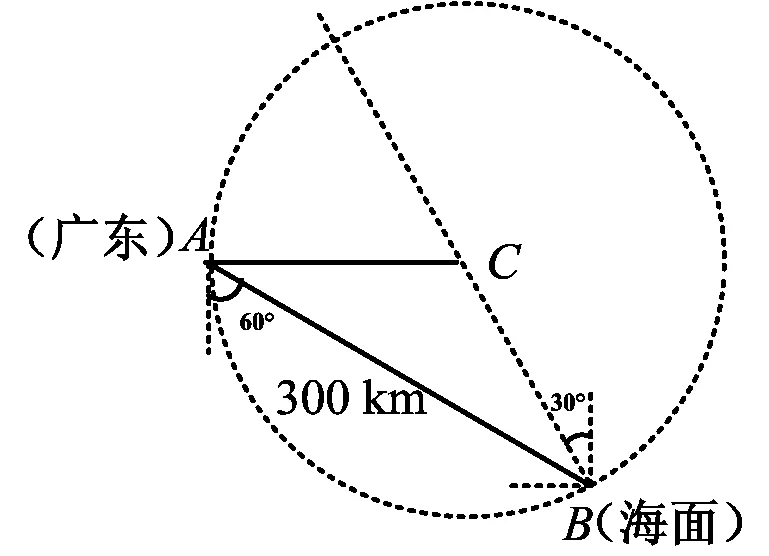
图1

生(众)：只要求出图1所示BC的长度，除以速度就可以求出时间.

接着从实际问题中抽象出数学问题：解三角形，并给出定义.一般地，把三角形的3个角A，B，C和它们的对边a，b，c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫解三角形.

设计意图本环节通过实际问题导入，不但调节了课堂氛围，激发了学生的学习兴趣，而且教会学生从实际问题中抽象出数学问题的能力，并尝试建立数学模型即解三角形.

素养目标培养学生的数学抽象和数学建模能力.

2.2 探究证明

问题2如何解决上述问题？

生1：可以猜出来.

师：猜想是数学的源泉，你能说明一下你猜的方法吗？

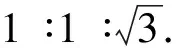
师：非常好，你能回答一下初中学习过的解三角形有哪些方法吗？

生2：有勾股定理、内角和定理.

师：其他同学有补充吗？

生(众)：还有三角函数.

师：在Rt△ABC中，∠C=90°,正弦函数sinA=______;sinB=______.

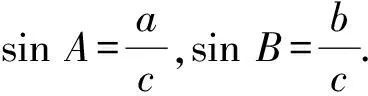
师：谁能将这两个式子整理成一个？

师：这个式子能不能表示得更加完美？

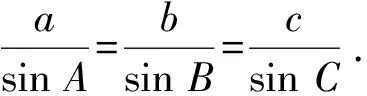
师：这个等比式在锐角或者钝角三角形中是否成立呢？

为了验证猜想是否可行，通过计算机数据分析,拖动点A改变三角形形状(几何画板演示略)，可以发现比值始终相等.

师：我们该如何证明呢？

为了引导学生更顺利地想到证明方法，此处特地引入中国数学文化“梅文鼎老先生指出：西法用三角，犹古法之用勾股也.但三角有钝角，而勾股无之，论者遂谓勾股之数有所穷，殊不知锐角形须分为两勾股，钝角形须补成勾股知……，然则勾股虽不能备三角之形，而能兼三角之理，三角不能出勾股之外，而能尽勾股之用，一而二，二而一者也.”一方面激发学生的民族自豪感，另一方面从中吸取一些古人的宝贵意见.

学生分组讨论探究锐角和钝角三角形中的正弦定理.

1)锐角三角形.

如图2，过点C作CD⊥AB于点D,则

CD=asinB=bsinA,

因此

同理可得

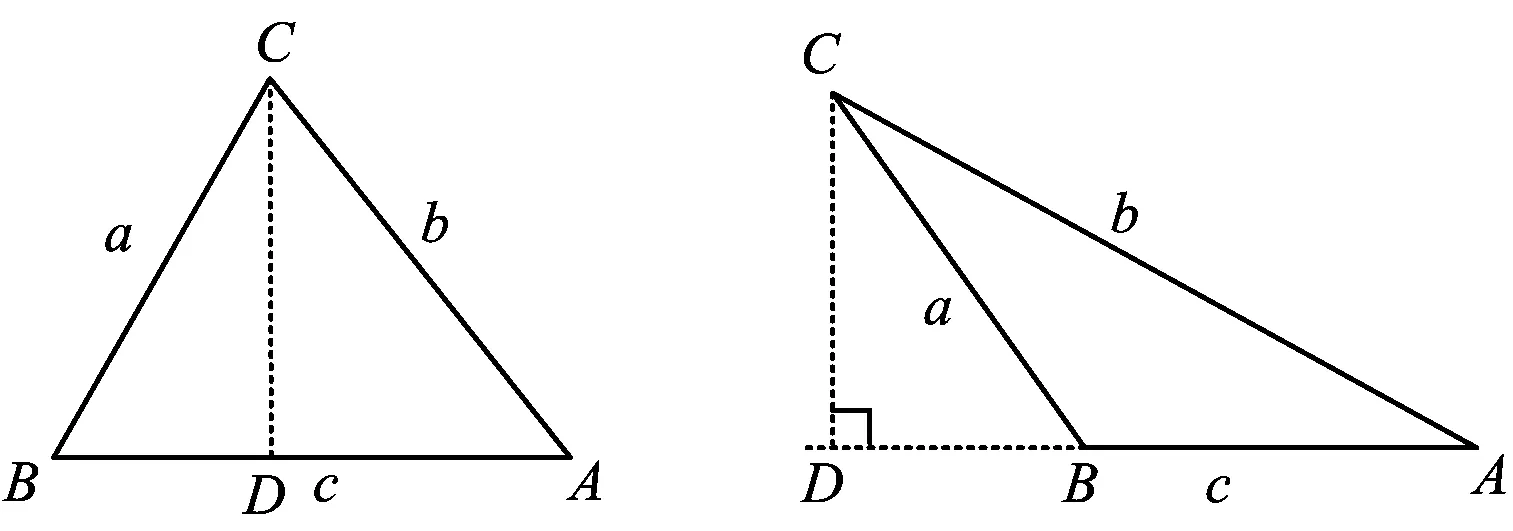
图2 图3

2)钝角三角形.

如图3，与锐角三角形相比，相同之处：原理、转化的思想；不同之处：sinB的表示，即

设计意图引导学生结合初中直角三角形中的边角关系，通过观察、比较、分析及从特殊到一般的推理方法发现并证明正弦定理.采用分组探究的方式，利用几何画板，借助数据分析大胆猜想，然后严谨论证.

素养目标培养学生的数据分析和逻辑推理能力.

2.3 定理应用

例1在△ABC中，已知A=45°,B=75°,a=30,解三角形.

应用1已知三角形的任意两个角与一边求解三角形问题.

例2在△ABC中，已知B=30°,c=300,b=150,求a.

应用2已知三角形的两边与其中一边的对角求解三角形问题.

回归课前提出的问题，解决台风到达时间的问题.在解决两边与其中一边的对角问题时又出现新的问题：解的个数问题.

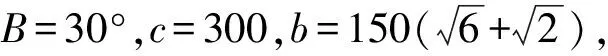
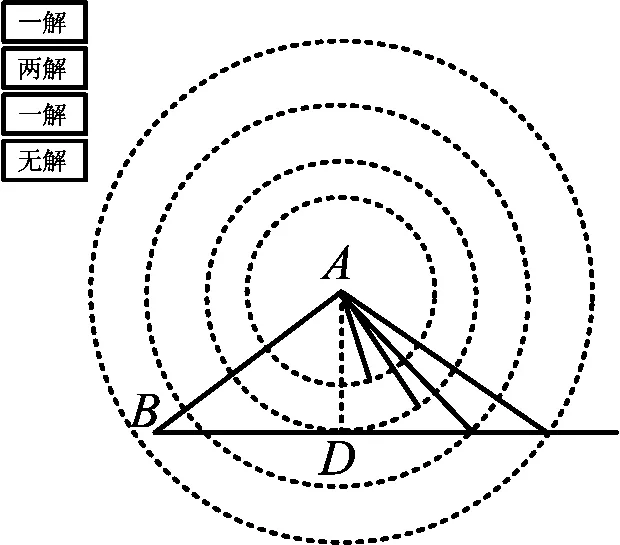
图4

通过改变台风半径思考解的个数的实际意义，并利用几何画板动态展示(如图4)归纳出当给定一个锐角和一边时，判断三角形解的个数的更一般性结论.

变式3若将变式2中的b改为100，请判断三角形解的个数.

设计意图通过例题与变式让学生在应用定理解决问题的过程中更深入地理解定理及其作用.并通过实际例子发现多解的意义及判断多解的一般方法.

素养目标培养学生的数学运算和直观想象能力.

2.4 反思探究

1)在三角形中，已知两边和其中一边的对角，当已知角是钝角或者直角时，如何判断三角形解的个数?

2)还有没有其他证明正弦定理的方法？

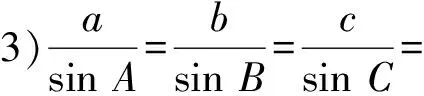
设计意图教师让学生类比“正弦定理得到的过程”，课后探究三角形解的个数问题及其他证明正弦定理的方法，很好地解决了课前疑惑，延伸了课堂，提升了课堂的深度和广度，并前后呼应，使得课堂内容更加丰满.

素养目标巩固学生的逻辑推理素养.

3 课后感悟

3.1 课堂气氛营造的技巧

好的课堂氛围有利于学生集中注意力，也有利于激发学习动力，更有利于消除疲劳,加速学生接受和消化课堂上的内容.

由于借班上课与学生接触时间短，为了迅速与学生打成一片，并取得学生的信任，提升学生信心，本节课中笔者采用了下面的方式：

师：高一年级最优秀的班级是哪一个啊？

生(众)：我们班.

师：那肯定的，既然这样我请几位同学回答一下课前热身的答案.

生(众)：……

师：果然如此，我们班真的名不虚传啊！

好的课堂氛围需要教师的亲和力和个人魅力，笔者在中国文化渗透的环节，本来只是介绍梅文鼎证明了正弦定理的过程，反复思考后觉得如果只是叙述这件事，学生必然不感兴趣，因此将这段内容杜撰成一个故事.

比起干巴巴的叙述，杜撰的故事会显得更加生动，容易调动学生的注意力.数学文化的渗透不但使得学生的民族自豪感油然而生，而且对于下个证明环节有很好的提示作用.

3.2 课堂环节衔接的方法

为了让课堂环节更加紧凑、精彩，在设置时无外乎需要有两条线，一条明线与一条暗线，然后做到前后呼应.

本节课的明线：实际问题—数学问题—回顾初中—观察直角—猜想验证—推理证明—定理应用—出现问题—解决提升—课后探究—课后反思.

暗线：数学抽象—数学建模—数据分析—逻辑推理—数学运算—直观想象.

从这样两条线出发，课堂环节就变得非常严谨，又前后呼应.整个流程环环相扣，如行云流水.

3.3 课堂精准体现的方式

精准的课堂需要体现学生的学习效果，有时轰轰烈烈的课堂确实很有氛围，但是如果不能收到成效，那么核心素养的培养也就宣告失败了.如何在课堂中评价学习的效果呢？本节课采用了提问、板演、互批、互助、单独辅导的方式，让学生暴露问题，互相指出问题，互相探讨问题，师生交流问题.这种方式不但可以掌握学生学习的情况，更让学生在学习过程中悟出道理，互相讲解道理，加深印象，从而更好地掌握知识和运用知识，习得学习知识的方法，正所谓“授人以渔”[1].

3.4 课堂有效提问的办法

教学过程是不断提出问题和解决问题的活动.问题是数学的心脏，问题设计要体现数学的本质，贴近学生的最近思维发展区，这样才能驱动学生思考和参与课堂[2].

例如，为了引导学生在直角三角形中发现正弦定理，笔者的提问是：

1)初中阶段我们解三角形时用到哪些方法？

2)这些方法中体现边角关系的有哪些？

这样的提问既不会让学生随口而答，也不是“镜花水月够不着”，学生通过思考可以逐步发现正弦定理.

3.5 课堂生成问题的处理

课堂生成是课堂生命的体现，是学生思维火花碰撞的很好表现，也是课堂预设外教师处理问题能力的展示.

本节课现场生成了如下几个环节：

1)在实际问题引出数学问题后，笔者提出“如何解这样的三角形”，预设学生的回答是“不知道”，然后进一步追问初中阶段解三角形的方法.

课堂生成：有学生直接猜出了答案.

本节课的处理：大力表扬学生大胆猜想的方式，为接下来从直角三角形中得到定理以及在任意三角形中得到定理的猜想作好铺垫，最后在解决了这个实际问题后再次对前面这位得出猜想的学生进行表扬，收到了很好的呼应效果.

2)在解决了两边及其一边所对角的问题之后，笔者请了一位学生类比解决任意两角一边问题并归纳出正弦定理的第二个应用.而被提问的学生由于腼腆不敢回答，笔者在整堂课结束时再次提问这位学生，并进行鼓励，最后他很好地回答了所提出的问题.面对这样的课堂生成，笔者的处理方式是努力做到不遗漏每一个学生.