2019年浙江省数学高考第16题深度赏析
(吴兴高级中学,浙江 湖州 313000)
1 原题再现

(2019年浙江省数学高考试题第16题)
本题是填空题压轴题,是2008年浙江省数学高考理科试题第15题、2017年浙江省数学高考试题第17题的升级版,对考生的数学能力有较高要求.本题以函数为背景,以绝对值、不等式、存在性问题等为载体,重点考查学生分类讨论、转化化归、数形结合等思想,以及对数学本质的理解.
2 解法赏析
本题有着丰富的内涵,可以从一题多解、多题归一、函数思想、导数思想、解集、数形结合、纵向距离等多维度去审视,从而得到不同的解法,可谓横看成岭侧成峰.例1是求最大值,故以下解法只需考虑a>0的情形.
2.1 函数思想
解法1f(t+2)-f(t)=
a(t+2)3-(t+2)-at3+t=
a(t+2)3-at3-2,
设g(t)=a(t+2)3-at3-2,则
g′(t)=3a(t+2)2-3at2=12a(t+1).
因为要求a的最大值,不妨设a>0,则当t≥-1时,g′(t)≥0,g(t)单调递增;当t≤-1时,g′(t)≤0,g(t)单调递减,所以
g(t)min=g(-1)=2a-2.
由题意知只需

点评导数是研究函数的有力工具,利用导数求最值可以避免因为化简而导致的错误,比较适合学生的思维习惯.
解法2f(t+2)-f(t)=a(t+2)3-at3-2=
6at2+12at+8a-2,
设g(t)=6at2+12at+8a-2,其中a>0,则
下同解法1(略).
点评通过化简将问题转化为二次函数问题,利用二次函数的性质进行求解,从而将问题化归为熟悉的背景,使问题顺利求解.
2.2 参数分离思想
解法3由解法2得
f(t+2)-f(t)=6at2+12at+8a-2,
则
即
亦即
从而
设m=6t2+12t+8=6(t+1)2+2,则m∈[2,+∞),于是
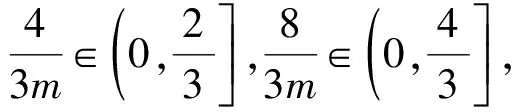
点评解法3从绝对值不等式的解法入手,结合参数分离思想,解法自然,是解决存在性问题的常用方法之一.
2.3 数形结合思想
解法4同解法3,设m=6t2+12t+8=6(t+1)2+2,则m∈[2,+∞).由题意得
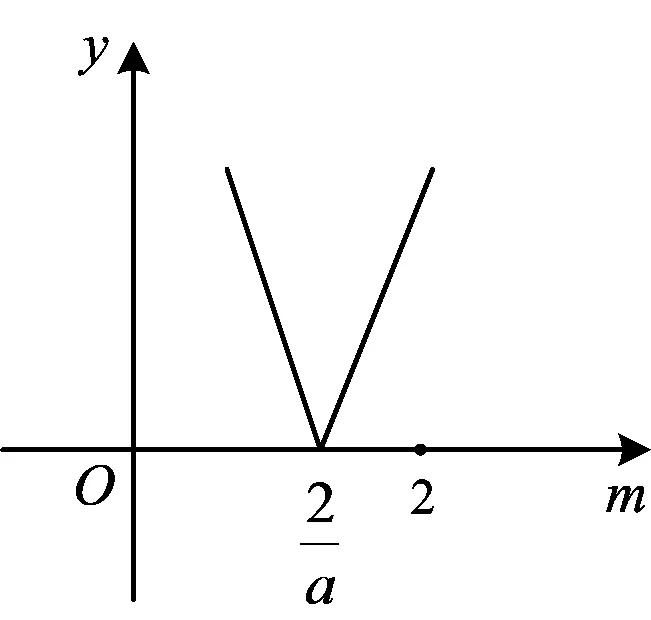
图1
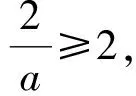
g(m)min=g(2)=2a-2,
从而
于是
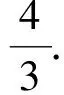
点评通过换元,实现了降维,从原题的三次函数降到了一次,结合绝对值一次函数的图像,使得问题得以快速解决,极大地减少了思维量,解法简洁流畅.
2.4 分类讨论思想
解法5同解法4,设a>0,则

g(m)=am-2,
从而
g(m)min=g(2)=2a-2,
于是
即
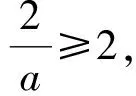
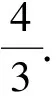
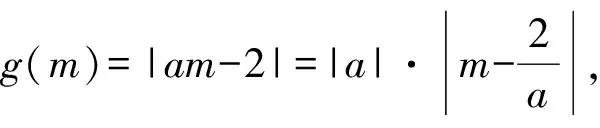

从而
g(m)min=2a-2.
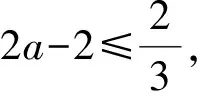
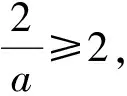
从而g(m)min=0,满足题意.
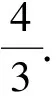
点评解法5从绝对值的定义出发,通过分类讨论,求出a的最大值,有利于学生对数学本质的理解.
此题是研究含绝对值的函数的最值问题.若考虑去绝对值,则原函数可以转化为一个分段函数来讨论,即解法5.若从绝对值的本质去思考,做一个代换,则可以转化为数轴上的问题来解决,化归为绝对值的本质,即解法6,解题变得极为简洁、直观,而这一思想与2008年浙江省数学高考理科试题第15题一脉相承.
2.5 纵向距离

解法7由解法3知
即
设r(t)=3at2+6tat,s(t)=-4a+1,其中a>0,则
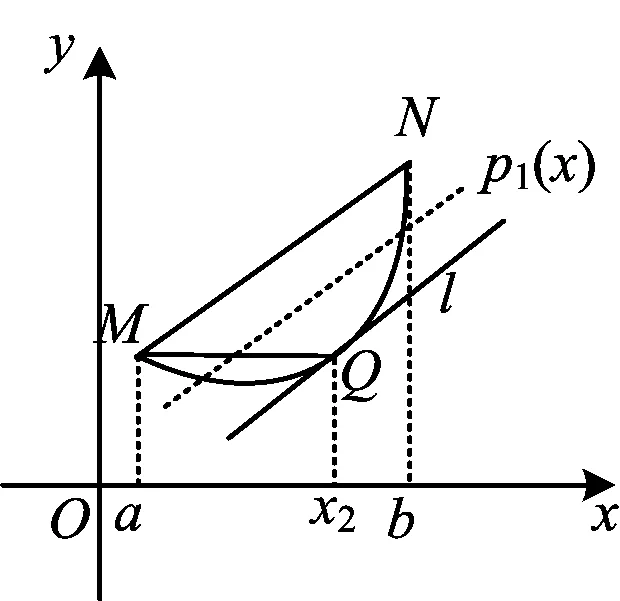
又r(t)min=r(-1)=-3a,若0 即 点评若直接利用纵向距离处理|f(t+2)-f(t)|,则不易于把握,因此解法7化简后再构造两个函数,这时纵向距离便简单直观了,合理构造函数是利用纵向距离的关键. 解法8由解法5,得 设r(t)=3at2,s(t)=-6at-4a+1,其中a>0,则 设T(x0,y0)∈r(t),则r(t)在T处与s(t)平行的切线的斜率为 k=r′(t)|t=x0=6ax0, 即 6ax0=-6a, 从而x0=-1,于是T(-1,3a).又s(-1)=2a+1,因此纵向距离的最小值为 3a-2a-1=a-1. 点评解法8是解法7的升级版,阐述了更一般情形下纵向距离的解法.解法7与解法8体现了函数及数形结合的思想,都是从纵向距离的视角来解决问题,因所构造函数的差异,纵向距离求法有所不同,但其本质不变.从距离的视角来解读绝对值,为我们解决绝对值问题打开了一扇新的窗,提供了一种新的思路与方法,与2017年浙江省数学高考试题第17题如出一辙. 一题多解是解题教学中常用的策略之一.但只为了解题而一题多解,则无法真正提高学生的核心素养,对于经典试题我们要有敬畏之心,要适度拓展与引申,充分发挥其教育功能.在数学教学中,如果能以某一主题为中心,注意把“一题多解”“多题归一”等方法组成一个互相联系、互相作用的综合体,更有助于加深知识的掌握与巩固,提高解题技巧及分析问题、解决问题的能力,增强思维的灵活性、变通性和创新性,从而实现整体功能大于部分功能之和. 图2 设函数f(x)在[a,b]上有二阶导数,且f″(x)在[a,b]上恒正或恒负,则存在f(x)在[a,b]上的线性最佳一致逼近多项式p1(x). p1(x)的几何意义:如图2,直线l∥MN与f′(x)切于点Q,直线y=p1(x)与弦MN平行,且过线段MQ的中点,其方程为 图3 结论1如图3,若f(x)的图像是平口单峰函数,此时图像的特征为: 1)kMN=0,Q为f(x)的极值点; 2)f(a)=f(b); 3)直线l即p1(x)处于正中间; 结论2若f(x)的图像不是平口单峰函数,则构造为平口单峰函数. 利用切比雪夫最佳函数逼近理论,解决形如|f(x)-g(x)|的问题,从而实现“多题归一”,即从纵向距离的视角进行解读,不仅给学生一种解法,更给学生一种思想、一种工具.为强化纵向距离的应用,以下各题只讨论纵向距离解法. 考点1函数最大值的最小值问题. 例2已知函数f(x)=x2+ax+b(其中a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值. 1)证明:当|a|≥2时,M(a,b)≥2; 2)略. (2015年浙江省数学高考理科试题第18题) 不妨设a<0,则 g(-1)=1-a,g(1)=1+a, 从而 当且仅当g(-1),g(1)与h(x)距离相等时等号成立. 点评最大值的最小值问题,是近几年浙江卷的一个热点问题,在解法上更多的是从绝对值三角不等式入手.本证法则是以纵向距离为入口,凸显数与形的完美结合,给人以美的享受.本题考查的区间是一个单调区间,因此也只需考查区间端点的函数值. 考点2函数中的参数问题. 例3已知t为常数,函数y=|x2-2x-t|在区间[0,3]上的最大值为2,则t=______. (2008年浙江省数学高考理科试题第15题) 解设f(x)=x2-2x,g(x)=t,函数在区间[0,3]上的最大值为2,即f(x)与g(x)的纵向距离的最大值为2. 因为f(0)=0,f(3)=3,f(1)=-1,所以 即t=1. 点评二次函数问题是高考的热点,也是难点.纵向距离解法丰富了二次函数问题的解法,给人耳目一新之感. 对于同一题,通过一题多解,从不同的角度去分析思考,会得到不同的启示.根据题中涉及到的不同的知识点适度引申,可使学生的思维触角伸向不同的知识领域,从而加深对知识的理解,发展学生的发散思维能力. 1)从函数的本质出发,结合导数及二次函数模型,便自然有了解法1和解法2. 2)从解绝对值不等式出发,结合存在性问题解法,便有了解法3. 3)根据绝对值运算的性质,对含参的绝对值问题,分类去绝对值符号是含参绝对值运算的基础,自然将我们引向分类讨论的思想方法,从而便有了解法4~6. 4)由绝对值的几何意义,将问题转化为数轴上两点的距离,从而有了解法6,这种转化与降维思想,是数学解题的常用策略之一. 5)解法7和解法8充分体现了数学概念的本质在解题中的应用,是转化与化归思想的具体应用,是从数与形两个维度对函数进行解读,充分体现了函数思想与数形结合思想在解题中的重要地位,是对绝对值的理性思考,是对数学本质的进一步升华. 解题教学在高中数学教学中有着重要地位,不仅要提倡一题多解,将数学的知识、数学与方法串联起来,形成知识体系,更要关注“多题归一”,关注试题背后所隐含的东西.通过拓展引申,将学生带向新的领域,让学生去领略新的盛景,发散学生的思维. 本文通过对例1的8种解法,建构绝对值函数的知识体系,通过链接历年高考试题将原题拓展引申,不仅可以强化学生对此类题模型的认识与理解,还可以激活学生的思维,特别是纵向距离方法的应用,为学生打开了一扇窗,也为解题教学研究提供了一种范式. 研题是有效的教研形式.活动中将命题、解题、析考、论教(学)融于一体,使得集体的智慧得以充分发挥,营造了良好的教研氛围,凸显了教研的校本特征,有利于促进教师内化课程基本理念、领会教学指导思想、把握学科课程本质、感悟考试评价方向、决策教学策略方法、提高教研与教学的针对性,从而促进课堂教学的有效性,促进教师的专业发展. 一题一处景,横看成岭侧成峰,经典试题一定有其丰富的内涵与深刻的背景,我们向经典致敬,不应只是对美景钦羡而驻足不前,而是要“寻根”“究底”,只有这样才能跳出“只缘身在此山中”的尴尬.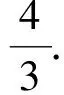
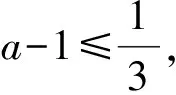
3 拓展引申
3.1 切比雪夫最佳函数逼近理论简介
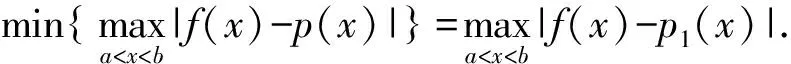

3.2 高考试题中的纵向距离
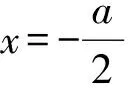
4 反思感悟
4.1 反思解法
4.2 反思教学
4.3 反思教研

