一题一乾坤 素养即世界——以2019年浙江省数学高考试题第17题为例

(杭州师范大学附属中学，浙江 杭州 310030)(鲁迅中学，浙江 绍兴 312000)

2019年是浙江省新一轮高考改革数学文理合卷考试的第3年.2019年浙江省数学高考试卷的形式与结构保持稳定；稳在基础与重点，稳中有变、变中有新；注重基础知识、主干知识的考查，又侧重于知识的内在联系，在知识的交汇处匠心独具，为不同层次的考生提供了相应的思考空间，获得不同的发展；试题渐次推进，入口容易深入难，注重学生的思维品质、学科素养的考查，有较高的区分度.填空压轴题第17题是一道向量题，向量题已经成为浙江特色，“源于课本又高于课本”，韵味独特、立意清新；突出考查了平面向量的线性运算、平面向量的基本定理，突出基底意识、模的运算、坐标运算，需要考生具备逻辑推理、直观想象、数学运算、数学建模、数据分析等数学核心素养，可谓简约而不简单！

1 试题分析

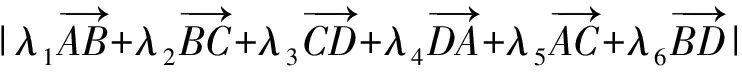
(2019年浙江省数学高考试题第17题)

解法1(基本定理+模的运算+数据分析) 由正方形ABCD的边长为1，得

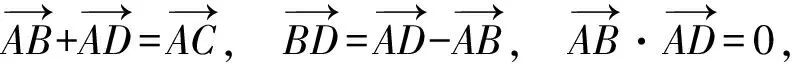
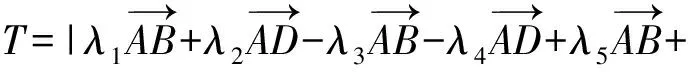
由于λi(其中i=1，2，3，4，5，6)取遍±1，可得

λ1-λ3+λ5-λ6=0，λ2-λ4+λ5+λ6=0，

取λ1=λ3=λ4=λ5=λ6=1，λ2=-1，得所求最小值为0.

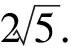
解法2(基本定理+局部消元+数据分析)

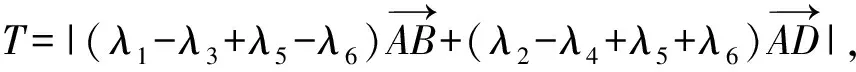
|λ1-λ3+λ5-λ6|=|λ2-λ4+λ5+λ6|=0.

此时T=0，其中等号成立的条件为λ1=λ3=λ4=λ5=λ6=1,λ2=-1.

要使得T最大，只需|λ1-λ3+2|，|λ2-λ4|最大，即

|λ1-λ3+2|=4， |λ2-λ4|=2,

从而

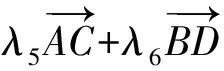
解法3(基底意识+模的运算+先局部再整体数据分析)

由于|λ5-λ6|,|λ5+λ6|中必有一个为0，一个为2，且λ1-λ3∈{-2,0,2}，λ2-λ4∈{-2,0,2},因此

当λ1+λ5=λ3+λ6=λ2+λ5=λ4-λ6=0时，取λ1=λ3=λ2=1,λ5=λ6=λ4=-1，得Tmin=0.

解法4(基底意识+模的运算+部分变量定值法再整体数据分析，运用减少变量的思想)

不妨设λ5=λ6=1，则

评注解法1～4将向量问题化归为基底的选择与优化问题，其次转化成根号下多变量平方和的最值问题，减少变量、局部变量赋值、变量取值讨论等都是问题解决的好方法，注重数学直觉和猜想能力，培养数感.

解法5(基底意识+模的运算+数据分析)

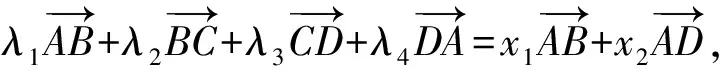
于是

解法6(坐标法+模的运算+数据分析)

以A为坐标原点、AB为x轴、AD为y轴建立直角坐标系，则A(0,0),B(1,0),C(1,1),D(0,1),从而

接下来处理的步骤同解法1～4.

评注坐标法是解析几何思想的重要体现，是解决向量问题的好方法.

解法7(几何法—位移—绕来绕去的向量，从物理角度建立数学模型)

位移最小：绕成两个三角形，位移为0，故Tmin=0(如图1)；

图1 图2 图3

解法8(几何法—位移—绕来绕去的向量，从物理角度建立数学模型)

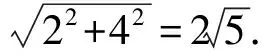
2 探源与改编

基础和经典不怕重复，注重技巧和包装的题目永远只能是昙花一现，经不起时间的考验.2019年浙江省向量题所蕴含的思想方法和代数特征有迹可循，可以从以前的竞赛题和高考题中找到它的影子：

2.1 从位移角度探源

例2某动点在直角坐标系第一象限的整点上运动(含第一象限x,y轴上的整点)，其运动规律为(m,n)→(m+1,n+1)或者(m,n)→(m+1,n-1).若该动点从原点出发，6步运动到点(6,2)，则有______步不同的运动轨迹(答案：9).

(2013年浙江省数学竞赛试题第17题)

例3设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动质点落在点(3，0)(允许重复过此点)处，则质点不同的运动方法共有______种(答案：5).

(2004年浙江省数学高考理科试题第15题)

例1可以拓展为：

例1还可以改编为：

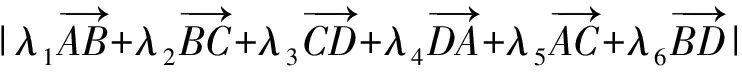
2.2 从数据分析和绝对值形式探源

绝对值以及多变量的最值(范围)问题在2016年浙江省数学高考卷中就有出现，很好地考查了学生数据分析的能力.赋值分析是一种很好的数感体现，考查数学思维和数据分析素养.

例6已知实数a，b，c,

( )

A．若|a2+b+c|+|a+b2+c|≤1，则a2+b2+c2<100

B．若|a2+b+c|+|a2+b-c|≤1，则a2+b2+c2<100

C．若|a+b+c2|+|a+b-c2|≤1，则a2+b2+c2<100

D．若|a2+b+c|+|a+b2-c|≤1，则a2+b2+c2<100

(2016年浙江省数学高考理科试题第8题)

分析在选项A中，令a=b=10,c=-110;在选项B中，令a=10,b=-100,c=0;在选项C中，令a=100,b=-100,c=0,即可排除这3个选项.故选D.

3 悟题思教,回归本质

2019年浙江的向量题可以说又是一道好的高考题.好的高考题之所以成为经典，是因为它可以让学生学会更好地解题，让教师能更好地教数学.一道好的高考题，考的就是数学的核心素养.

3.1 观题悟题

学会观题，用数学的眼光观察世界.要学会观数学题，根据题目的表述分析它到底想考什么知识点，从而构建合适的解题路径，选择合适的方法.浙江省的向量试题一直有它独特的味道，简约而不简单，围绕向量的两大主线：代数与几何.代数的本质是数与多项式，几何的本质是位移；以几何图形为研究对象，通过研究图形方法、思想统整几何代数内容形成主线，以多项式运算应用、向量代数体系建立及其应用形成辅线，建立数学基本模型.

3.2 感悟方法

研究图形的基本方法主要有4种：1)综合几何方法，其中几何基本图形包括直线、平面图形(三角形、四边形、圆、圆锥曲线)、空间图形；几何基本位置关系包括平行、垂直，图形度量关系包括距离(长度)、角度.2)解析几何方法，即坐标法.3)向量几何方法.4)微积分方法.

代数处理的方法主要是通过与数和多项式运算进行类比，感悟向量代数运算的特有规则，加强两个数感的培养，即代数式的结构分析与变形转化能力、数据分析能力.代数求解的策略有三点共线、四边形对角线向量、矩形大法、三项平方、极化恒等式、向量三角不等式(系数的拼凑)等.

( )

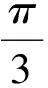
(2018年浙江省数学高考试题第9题)

分析对b2-4e·b+3=0进行代数结构分析可知这是二次方程的结构，想到因式分解，将代数式进行合理变形，变成b2-4e·b+3e2=0就可以因式分解了.

3.3 为素养而教

数学是思维的体操，教的不是题海，是思维，让学生参与问题求解的整个过程，总结提炼思想与方法，感悟数学问题中所蕴含的逻辑推理、数学运算、直观想象、数据分析、数学建模等核心素养.2019年全国及其他省份的向量题其代数形式和几何理解相对简单一些，素养的层次要求更集中一些，以坐标法、数量积、模的运算为主，突出向量所蕴含的逻辑推理、数学运算、直观想象等.难度在中等以及中等偏下，如：

( )

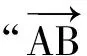
A.充分而不必要条件

B.必要而不充分条件

C.充分必要条件

D.既不充分也不必要条件

(2019年北京市数学高考理科试题第7题)

分析该题主要考查逻辑推理、数学运算能力，答案为C.

( )

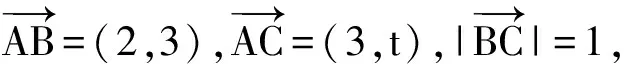
A．-3 B．-2 C．2 D．3

(2019年全国数学高考卷Ⅱ理科试题第3题)

分析该题主要考查数学运算、逻辑推理能力，答案为C.

例10已知向量a=(-4，3)，b=(6，m)，且a⊥b，则m=______.

(2019年北京市数学高考文科试题第9题)

分析该题主要考查数学抽象、数学运算能力，答案为8.

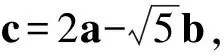
(2019年全国数学高考卷Ⅲ理科试题第13题)

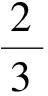
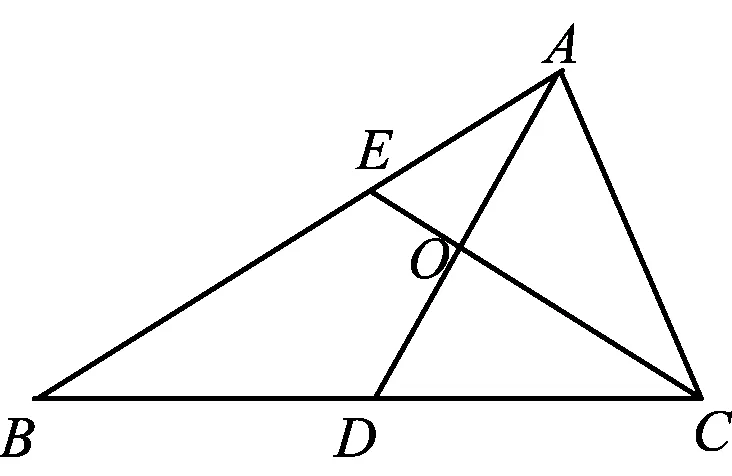
图4

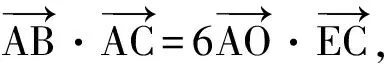
(2019年江苏省数学高考试题第12题)

例13已知非零向量a，b满足，|a|=2|b|,且(a-b)⊥b，则a与b的夹角为

( )

(2019年全国数学高考卷Ⅰ理科试题第7题)

分析该题主要考查逻辑推理、数学运算能力，答案为B.

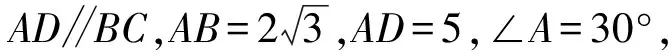
(2019年天津市数学高考理科试题第14题)

分析该题主要考查逻辑推理、数学运算、直观想象能力，答案为-1.

总之，在平面向量的教学中，既要关注其“数”的严谨，又要充分发挥其“形”的直观，以“两个定理”(共线定理和平面向量基本定理)为基点，以“四大运算”为主线，在推理的同时关注运算，在运算的过程中体会推理，使得数学运算、逻辑推理、数据分析以及几何直观等核心素养融为一体，相得益彰.在向量解题活动中，教师选好题，把握好难度，引导学生感悟数学思想方法，积累数学思维的经验，在潜移默化中形成和发展数学运算素养.