一个轨迹问题的多种探究——以椭圆焦点三角形内心轨迹为例

(天台中学,浙江 天台 317200)

研究动点的轨迹方程是解析几何的基本问题之一.解决与椭圆焦点三角形性质有关的问题，常要结合椭圆的定义、平面几何中的结论和解三角形的知识.这类问题在高考试题与竞赛题中经常出现，因此，对椭圆焦点三角形内心轨迹方程的研究是非常必要的[1].近期，笔者在所在学校高二备课组上了一节公开课“一个轨迹问题的多种探究”，现将这节课的教学实录、教后感悟整理如下.

1 问题提出

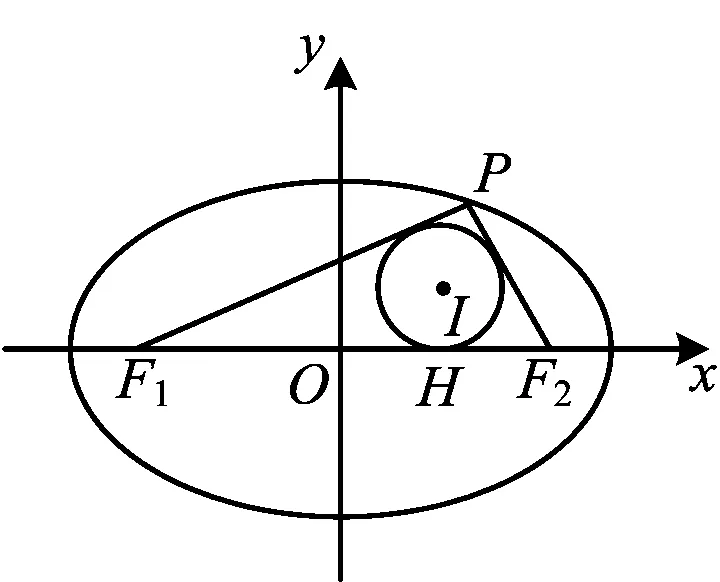
图1

2 教学实录

教师用PPT出示问题，师生共同分析已知条件，引导学生思考：△PF1F2内心的条件该如何使用？椭圆的性质可以用在哪里？点I的轨迹是什么？

探究1相关点法.

师：生1，请分享一下你的思路.

生1：先求点I的轨迹方程，由方程说明轨迹是什么，借助点P的轨迹方程求点I的轨迹方程.

师：很好！思路清晰，请你到讲台上讲一讲你的思考过程.

生1：设△PF1F2的内切圆与F1F2相切于点H，记椭圆的半长轴、半短轴、半焦距分别为a，b，c，椭圆的离心率为e,点P，H，I的坐标分别为P(x0,y0)，I(xI,yI)，H(xH,0).由题意知y0与yI同号，及

得

但点I的横坐标与点P的横坐标之间的关系还没有思考出来.

师：想法不错！有没有同学需要补充？

生2：由相切可知

|F1H|-|F2H|=|PF1|-|PF2|，

又由椭圆的焦半径公式

|PF1|=a+ex0, |PF2|=a-ex0,

可得

xI=xH=ex0.

师：非常好！这位同学很好地应用了椭圆中焦半径公式与内切圆的条件，得到横坐标之间的关系.由此可知，点I的轨迹方程是什么？它表示什么曲线？

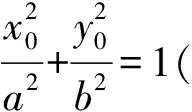
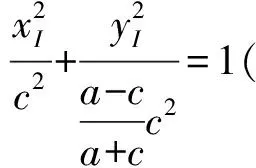
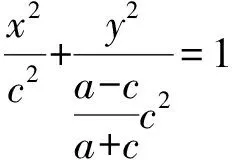
(1)

师：很好!我们用相关点法探究出了内心的轨迹方程.还可以借助几何画板，验证点I的轨迹，内心I的轨迹确实是一个椭圆.

评注从3位学生分享的思考过程来看，解这道题的关键是找到点I的坐标与点P的坐标之间的关系，纵坐标关系用等面积思想容易得到，难点在于如何得到横坐标之间的关系.学生在思考时，突破这一点有一定困难.由相切条件得知

|F1H|-|F2H|=|PF1|-|PF2|，

结合椭圆的焦半径公式

|PF1|=a+ex0， |PF2|=a-ex0,

巧妙地得到点I的横坐标与点P的横坐标的关系.

刚才我们已经探究出内心的轨迹及其方程，请大家继续思考，有没有解决该问题不同的想法？三角形的内心这个条件，是否可以换个角度来应用？

探究2向量角度法.

师：哪位同学说说你的想法？

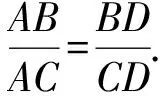
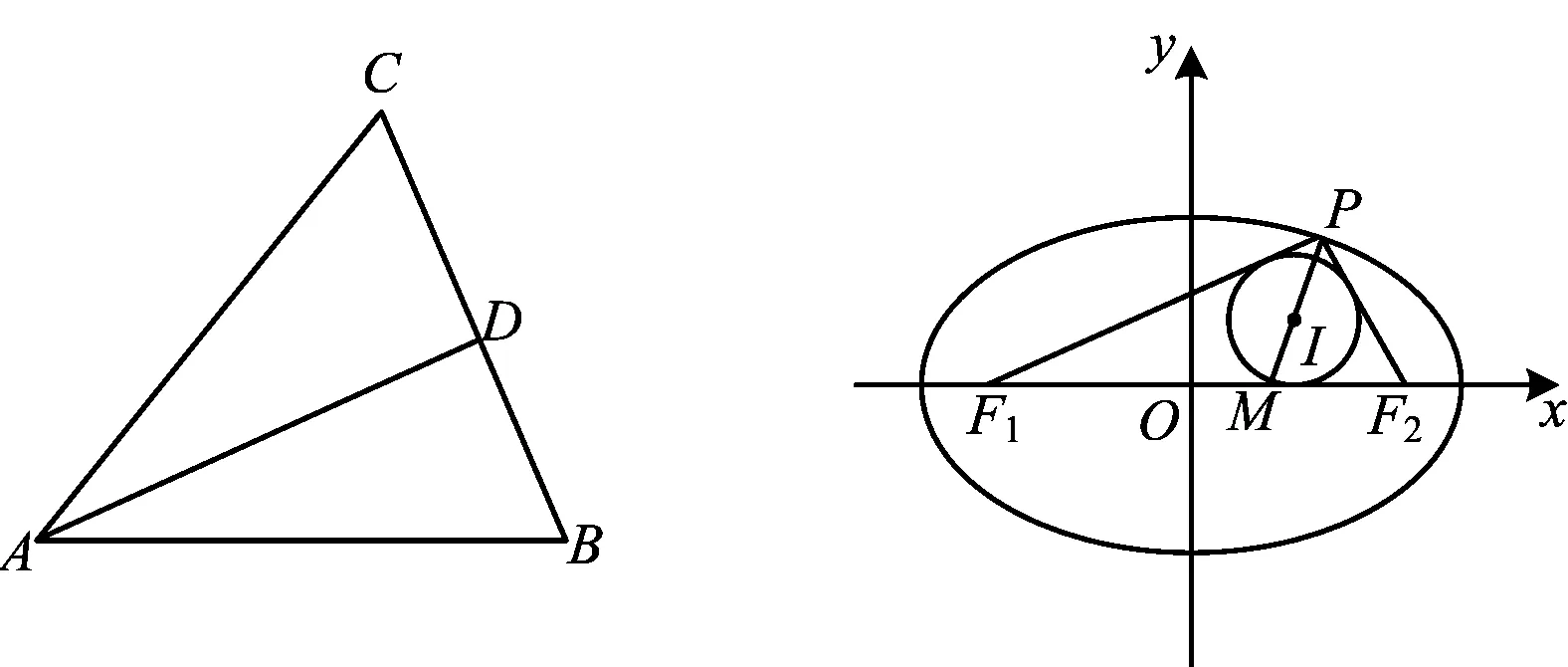
图2 图3

师：很有想法！我们能否利用三角形角平分线的性质得到点I的轨迹方程？大家先分组讨论，稍后请一位学生到讲台分享你的做法，并板演主要过程.

生5：设P(x0,y0)，I(xI,yI),延长线段PI交线段F1F2于点M，如图3所示，设M(xM,0)，在△PF1M与△PF2M中，由角平分线性质得

又由分式合比性质得

师：好主意！能想到线段的定比分点坐标公式，不错的想法！那如何能得到xM与x0的关系式呢？

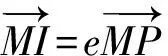
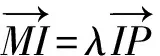
师：同学们，受到探究2的启发，平面向量的运用有时会把繁琐的解析几何问题转化为简单明了的代数问题，使代数和几何完美结合.

探究3妙用海伦公式.

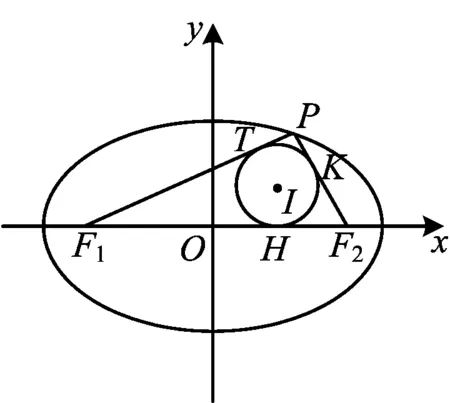
图4

师：哪位同学有新的想法，展示一下你的做法.

生7：如图4，设△PF1F2的内切圆与F1F2，PF1，PF2分别相切于H,T,K，内切圆半径为r，记|F1H|=m,|F2H|=n.同探究1中的设法，记△PF1F2的半周长为p,则

再由

|PF1|+|PF2|=|TF1|+|KF2|+|PT|+|PK|=

|F1H|+|F2H|+2|PT|,

可得

|PT|=|PK|=a-c，

于是想到可用海伦公式来计算S△PF1F2.

师：想法挺独到!请继续分享你的思考过程.

生7：可算得

p-|PF1|=p-|PT|-|F1H|=

(a+c)-(a-c)-m=2c-m=n,

p-|PF2|=p-|PK|-|F2H|=

(a+c)-(a-c)-n=2c-n=m,

由海伦公式得

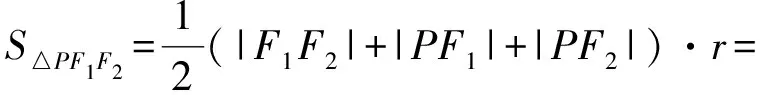
(a+c)·r，

从而

师：大家有没有发现什么？

化简即得方程(1).

师：太精彩了！

3 教后感悟

3.1 本节课的教学背景

这是高二年级上学期学完“圆锥曲线与方程”的章节复习课，授课对象是笔者所在学校钱学森班高二(1)班学生，学生基础好，思维敏捷.学生刚学完圆锥曲线的知识，能熟练掌握椭圆的性质，包括椭圆的第二定义及焦半径公式等，也熟悉求轨迹问题的主要步骤与常用方法，具备了一定的分析问题与解决问题的能力.基于此，笔者设计了这样一节“多种解法探究”课，提高学生综合运用知识解决问题的能力，培养学生对所学内容进行融会贯通的能力，培养学生类比、推广等探究能力[2].

3.2 教后反思

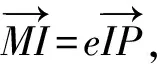
3.3 推广应用

通过对椭圆焦点三角形内心的轨迹及其方程的研究，可以将这种探究推广到新的“求动点的轨迹方程”的问题上，比如：

本文中探究1～探究3这3种方法均可应用到例2.还可以拓展到双曲线中：

1)当点P在双曲线的右支时，点I的轨迹方程为x=a(其中|y|

2)当点P在双曲线的左支时，点I的轨迹方程为x=-a(其中|y|