复合材料帽形加筋壁板剪切屈曲性能

汪厚冰，林国伟，韩雪冰，李新祥

中国飞机强度研究所 全尺寸飞机结构静力/疲劳航空科技重点实验室，西安 710065

飞机机身不同部位的受载情况如下：上部壁板的主要载荷为拉伸，下部壁板主要载荷为压缩，侧边壁板的主要载荷为剪切。根据载荷特点，设计机身壁板时所关注点不同，上部壁板主要考虑结构的疲劳问题，下壁板和侧壁板主要考虑结构的稳定性问题[1]。因此结构的稳定性是飞机设计关注的重点，为此欧盟制定了两个科研计划：欧盟第5框架计划[2](POSICOSS)和欧盟第6框架计划[3-4](COCOMAT),旨在开展将复合材料应用于飞机机身的结构稳定性研究，并为设计提供可靠的分析、计算方法和工具，在保证性能和寿命的基础上，大幅降低研发和使用费用。

在机身复合材料加筋壁板稳定性研究方面，关于压缩稳定性[5-10]的研究最多，包括试验、分析方法和数值模拟等。国内外学者和研究人员对剪切载荷作用下机身加筋壁板稳定性也进行了大量的研究[11-21]。臧伟锋等[11]使用“D”型夹具(试验件与夹具形成一个封闭的盒子)，在一端施加扭转载荷，从而实现了曲面加筋壁板的剪切。孙为民等[12]利用2件完全相同的加筋壁板形成一个封闭盒段，并在两端分别连接加载盒段和支持盒段，通过对加载盒段施加扭转载荷实现对加筋壁板的剪切。Wagner等[13-14]在20世纪30年代建立“对角拉”的方法，该方法主要用于平板及平面加筋壁板的剪切屈曲试验，由于四周夹具刚度较大，后屈曲阶段会影响试验件的变形，对试验件会引入额外的载荷。Rothwell[15]在此基础上建立了“三点梁”的剪切方法(在梁上的三点处施加载荷)，允许试验件端头变形，用此方法可进行剪切的后屈曲试验。Cricri等[16]在“对角拉”方法的基础上给每个角增加了铰连接，减小了试验件进入后屈曲四周夹具给试验件的额外拉力和弯矩，提高了试验的精度并扩展了“对角拉”方法的适用范围。冯宇等[17]用“对角拉”方法进行了复合材料T型加筋壁板试验，并用理论公式和数值模拟方法进行屈曲分析。Jung和Han[18]用一种改进的8节点壳单元分析了复合材料层压板的剪切屈曲。Ge等[19]对复合材料加筋壁板剪切进行了试验和有限元分析研究。Cordisco[20]和Abramovich[21]等利用试验机进行了复合材料帽形加筋壁板的剪切屈曲和后屈曲试验研究。

本文采用分布式剪切加载方法[22]，即在加筋壁板两侧边进行多点加载，每边加载点的载荷相同，避免了“对角拉”剪切试验方法中钉传载的不均匀[23-28]。根据复合材料的线弹性理论，推导了复合材料加筋壁板蒙皮的应变分布，并用试验结果进行了验证。采用理论公式、半经验公式对复合材料帽形加筋壁板的屈曲进行了分析计算，并将计算结果与试验结果进行对比，给出了实用的复合材料帽形加筋壁板稳定性分析方法。在数值分析中采用特征值法和几何非线性静态分析方法对复合材料加筋壁板的屈曲进行了分析。

1 试验件及试验方法

1.1 试验件

加筋壁板的试验件主要由蒙皮、长桁、框、加强片及约束端头等构成，如图1和图2所示，其中蒙皮、长桁和加强片为复合材料，材料体系为M21E/环氧树脂，单层厚度为0.186 mm，单层材料刚度参数见表1；蒙皮、长桁、加强片的铺层顺序见表2，其铺层的0°沿长桁方向，见图2。

试验件中包含长桁5根，框2个。长桁的剖面为帽形，帽高为32 mm，长桁间距为210 mm。框由L形组件和Z形组件连接而成，框的材料为铝合金(2024-T42)，其弹性模量为72 345 MPa，泊松比为0.33。试验件在制造时长桁与蒙皮采用共固化工艺成型，框与蒙皮、框的L形组件与Z形组件均采用机械连接方式连接而成，框与长桁交叉处，长桁连续，在L形型材上打孔。

为了保证试验件的四周在试验过程中不首先被破坏，试验件四边均进行加强，两侧边(与长桁平行，见图2)为主动加载区，连接了宽为106 mm的加强片，加强片的铺层见表2，加强片(共4块，一侧连接2块)比试验件蒙皮略厚，加强片与蒙皮采用共固化工艺成型。试验件的上下两端(见图2)为约束段，采用灌封加强，外围尺寸为1 288 mm×70 mm×100 mm(长桁方向)；灌封段四周为金属，材料为A3，其弹性模量为200 GPa，泊松比为0.3；灌注材料为掺铝粉的树脂，其弹性模量为10 GPa，泊松比为0.3。试验件考核段为1个框距(620 mm)，为了使考核段的受力状态与飞机结构中真实状态更接近，减小上下约束段对其的影响，将试验件在框的外侧各延伸250 mm，因此试验件的外围尺寸为1 288 mm×1 120 mm。

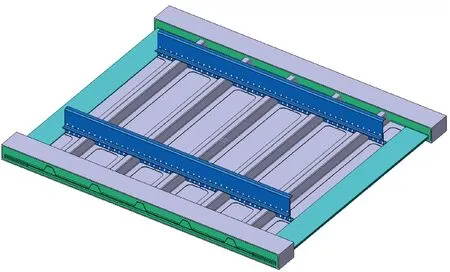
图1 试验壁板示意图Fig.1 Sketch of test panels

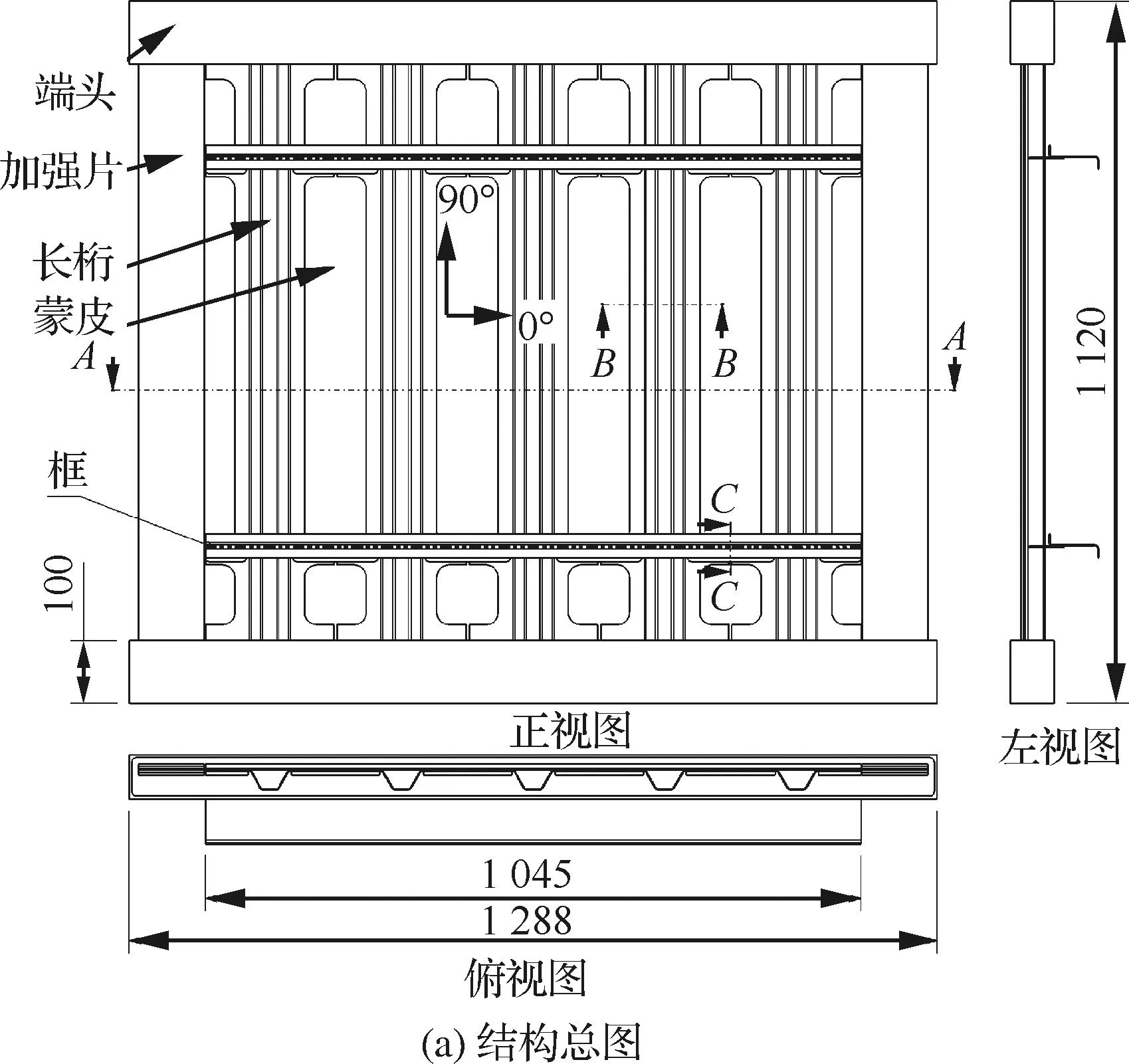
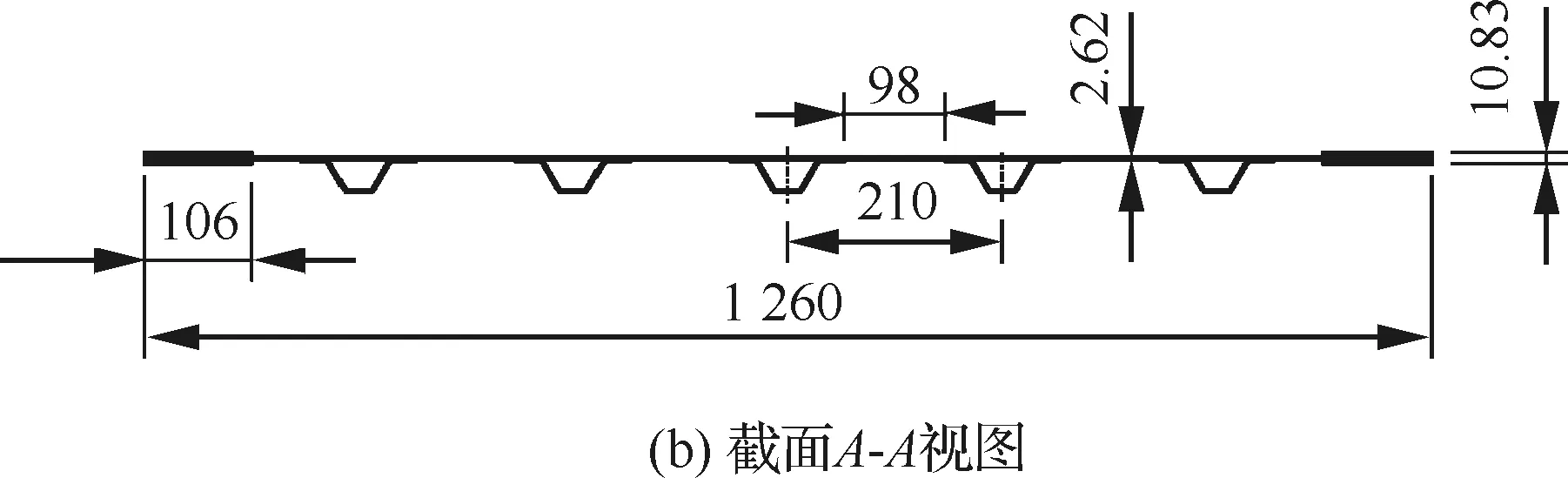
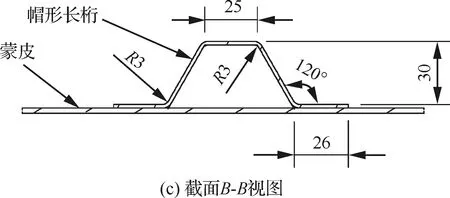
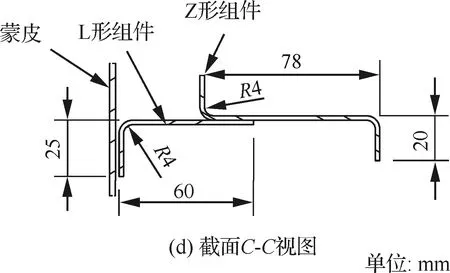
图2 试验壁板结构图Fig.2 Structure of test panels

表1 M21E/环氧树脂帽形加筋壁板单层材料参数Table 1 Parameters of lamina material properties of M21E/epoxy hat-stiffened panel

注:E11为纤维方向弹性模量;E22为垂直纤维方向的弹性模量;ν12为泊松比;G12为剪切模量。

表2 M21E/环氧树脂帽形加筋壁板的铺层顺序Table 2 Stacking sequence of M21E/epoxy hat-stiffened panel

1.2 试验方法

试验原理参见文献[22]。为了获取试验件蒙皮的应变分布，在蒙皮的3个截面(图3中的R1、R2、R3)粘贴应变计(能测量3个方向的应变)，所有应变计均背靠背粘贴，图3中括号外的编号为长桁侧(蒙皮内侧)应变计代号，括号内的编号为光面侧(蒙皮外侧)应变计代号，应变计编号最后一位代表应变计的不同方向，1代表0°方向(沿长桁反向)，2代表45°方向，3代表90°方向(沿框方向)。每个试验件共粘贴花形应变计24个。图3中C1～C4为应变计粘贴位置的列号，R1～R3为行号。

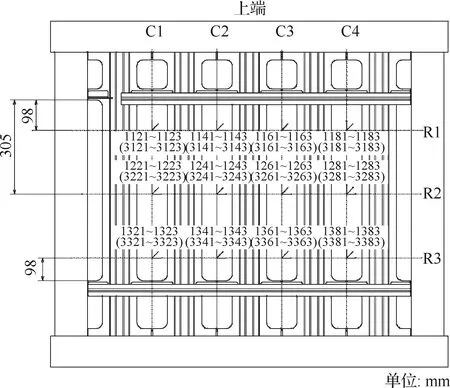
图3 试验壁板应变计布置图Fig.3 Strain gauge map of test panels

1.3 试验载荷和试验过程

加筋壁板的屈曲试验为静力试验，采用分步逐级缓慢加载，100%试验载荷为：顶边、底边载荷为423 kN，侧边载荷为370 kN。

在进行正式的屈曲试验前，先进行预试，确保试验件的安装状态正确和整个试验系统(包括加载夹具、控制设备、测量设备等)处于正常的工作状态。预试的最大载荷为30%试验载荷，加载级差为5%试验载荷，各加载级到了后保载3 s，逐级测量。正式试验先以5%试验载荷的加载级差逐级加载到60%试验载荷，再以1%试验载荷的加载级差逐级加载，根据获得的试验数据确定试验件是否屈曲，一旦发现试验件屈曲便停止继续加载，并按照加载级逐级卸载，加载和卸载过程中均逐级测量。

2 计算方法

2.1 蒙皮应变分布

加筋壁板在剪切载荷作用下，通常在蒙皮首先屈曲，因此蒙皮应变分布对研究加筋板的屈曲至关重要。复合材料帽形加筋壁板可看成由典型单元组成的重复结构，帽形加筋壁板典型单元见图4。典型单元的剪切刚度表达式为[29]

(GF)=A661s+2A662b2cosα+

A663b3+2A664b4

(1)

式中：b2、b3、b4分别为帽腰、帽顶、凸缘宽度；s为典型单元蒙皮宽度；α为帽腰和蒙皮间的夹角；A661、A662、A663、A664分别为蒙皮、帽腰、帽顶及凸缘的面内刚度系数，其计算表达式为

(2)

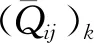
文献[29-31]研究表明，加筋壁板中不与蒙皮相连的部分承受的剪力部分很小，因此在计算复合材料加筋壁板的剪切刚度、等效剪切刚度和等效剪切模量时，可取筋条中与蒙皮相连部分和蒙皮进行计算。式(1)可简化为[29]

(GF)=A661s+2A664b4

(3)

由于复合材料层压板一直到破坏都呈现出良好的线弹性行为，因此根据线弹性理论[29](式(4))可推导出蒙皮的应变(式(5))。

(4)

(5)

式(4)～式(5)中：Q为帽形加筋壁板典型单元的剪力；(GF)s、γs分别为蒙皮剪切刚度(去凸缘连接区域)与应变；(GF)f、γf分别为凸缘剪切刚度(含与连接蒙皮连接区域)与应变；β为常数，其值可由式(6)计算得到：

(6)

图4 帽形加筋壁板典型单元Fig.4 Typical element of hat-stiffened panel

2.2 剪切屈曲计算

复合材料加筋壁板结构是由蒙皮、长桁及框组成，但长桁和框对加筋壁板剪切稳定性影响小，因此在进行剪切稳定性计算时仅考虑蒙皮的稳定性。计算前首先将蒙皮按照一定的方法分割成一系列的板条单元，然后对板元进行稳定性计算。计算模型做如下假设：长桁对蒙皮的支持为简支或固支，复合材料层压板近似为正交各向异性板(忽略拉-剪-扭的耦合效应)。

在面内均匀分布的剪切载荷作用下，正交各向异性矩形平板的屈曲控制方程为[29]

(7)

式中：x、y为复合材料层压板面内坐标系的两个坐标轴；D11、D12、D22、D66为复合材料层压板的弯曲刚度系数；Nx、Ny、Nxy为作用在复合材料层压板周边单位长度上的载荷；w为复合材料层压板的法向位移。

复合材料层压板的刚度系数为[29]

(8)

四边简支和四边固支条件下，矩形复合材料层压板的剪切屈曲载荷为[29]

(9)

式中：Nxycr为单位长度上剪切屈曲载荷；b为层压板的宽度；Ks为剪切屈曲系数，在简支与固支条件下其大小不同，剪切屈曲系数可查文献[29]得到。

除了理论方法计算剪切屈曲，还有半经验公式可计算加筋层压板蒙皮局部屈曲，其表达式为[29]

τxycr=6.9kS0(t/b)2

(10)

式中：τxycr为平均剪切屈曲应力，GPa；kS0为剪切屈曲系数；t为层压板蒙皮厚度。屈曲系数kS0与复合材料层压板的铺层百分比、边界条件(简支、固支)相关，其值可查文献[29]获取。

计算复合材料帽形加筋壁板屈曲载荷时需要将蒙皮离散成不同宽度的板条单元，如图5所示，蒙皮单元的宽度b通常的截取方法有3种：① 取长桁内间距；② 区凸缘中心距(对应于金属加筋壁板中相邻长桁凸缘的钉间距)；③ 长桁外间距。

图5 蒙皮宽度截取示意图Fig.5 Sketch of skin element width

3 数值分析

3.1 特征值分析法

特征值分析法用于线性屈曲分析，通过计算结构刚度矩阵奇异的特征值获取结构屈曲载荷和屈曲模态。ABAQUS有限元计算中有专门的特征值法计算模块(Buckling)用于屈曲分析。特征值分析法分两步计算，第1步为计算线性方程组，其表达式为[32]

K0u=P

(11)

式中：K0为预载荷下结构的弹性刚度矩阵；u、P分别为位移向量、载荷向量。

第2步为求解线性方程组[32]，获取特征值和特征向量，即

(K0+λKG)u=0

(12)

式中：KG为几何刚度矩阵；λ为屈曲载荷系数；u为特征值向量。用得到的λ乘以外载荷即为屈曲载荷。

3.2 几何非线性有限元分析方法

复合材料加筋壁板为薄壁结构，在剪切载荷作用下，结构可能发生大变形，尤其在屈曲时。为了更准确地分析结构变化，应当考虑结构的几何非线性。采用总体Lagrange描述方法建立结构的平衡方程为[32]

(13)

式中：σij和εij分别为应力和Green-Lagrange应变张量；ui为位移张量；ti和aij分别为面力和体力；dS和dV分别为面积和体积微元；0S和0V分别为初始构形的面积和体积。

所谓几何非线性即应变表达式中不仅有一次项，还有二次项，具体为[32]

(14)

应力应变关系即本构方程，其表达式为[32]

σij=Cijklεkl

(15)

式中：Cijkl为弹性模量张量。

非线性平衡方程可用Newton-Raphson增量分析方法求解，已知t时刻位形求取t+Δt时刻的位形，t+Δt时刻的位移、应力和应变可看成t时刻的位移、应力和应变与增量位移、应力和应变之和。

3.3 有限元模型

为了使数模模拟与试验更真实，有限元模型中包含整个试验件和部分夹具，如图6所示。试验件中的蒙皮、长桁和框外均采用壳单元模拟，上下支持端头的金属盒子也用壳单元，盒子内部的树脂采用实体单元。夹具主要包括与上支持端头连接的拉板和侧边加载板，模型中均采用壳单元。

试验件中各部分(蒙皮、长桁、框和两个支持端头)均采用Tie连接，保证各部分间的位移连续。试验件与夹具间均为机械连接，模型中采用Fastener模拟连接中的钉，Fastener单元的拉伸刚度和剪切刚度为[32]

(16)

图6 有限元模型Fig.6 Finite element model

式中:Kz为拉伸刚度；E为螺栓的弹性模量；A为螺栓截面积；l为螺栓长度；Kx和Ky为螺栓两个方向的剪切刚度；G为剪切模量；l0为螺栓的等效长度，单剪情况等效长度取被连接件总厚度的1/4，双剪情况取被连接件总厚度的1/8。

试验件下端头采用固支约束，框的两端约束法向位移。用1个参考点耦合与上端头连接拉板的左端面，并将载荷作用在参考点上，侧边加载点载荷的施加与拉板相同。

4 结果与对比

4.1 蒙皮应变分布

取载荷为300 kN(试验件上端载荷)时的剪切应变，用于比较试验结果、理论计算及有限元分析结果。载荷300 kN小于屈曲载荷，保证试验件的应变处于弹性阶段。试验剪切应变的计算表达式为

γ=ε0°+ε90°-2ε45°

(17)

式中：γ为剪切应变；ε0°、ε45°、ε90°分别为0°、45°、90°方向上的应变。3个试验件在300 kN载荷(上端拉力)作用下的应变分布见图7(图中应变为蒙皮内外侧剪应变的平均值)，有限元分析得到的应变分布见图8。可看出，由于加载夹具、支持夹具及框的支持等影响，试验件的蒙皮剪切应变相对均匀，不同部位稍有差异。

试验件在上端为300 kN载荷的剪切作用下，试验件剪切应变与理论计算剪切应变、有限元分析剪切应变(图8中蒙皮12处应变的平均值)的对比见表3，可看出，3个试验件的平均剪切应变很接近，表明试验控制的稳定性较好。试验的剪切应变与理论计算结果很接近，表明蒙皮应变的理论计算方法是正确的。有限元分析结果与试验的剪切应变(3个试验件的平均值3 721 με)也较接近，两者的误差小于5%，验证了有限元建模方法的准确性和有效性；有限元分析得到的剪切应变较试验平均应变略高，主要原因是模型中侧边加载夹具与试验件采用Fastener连接，未考虑摩擦、螺栓轴向力等因素，使得加载夹具对试验件的支持较实际结构弱一些。

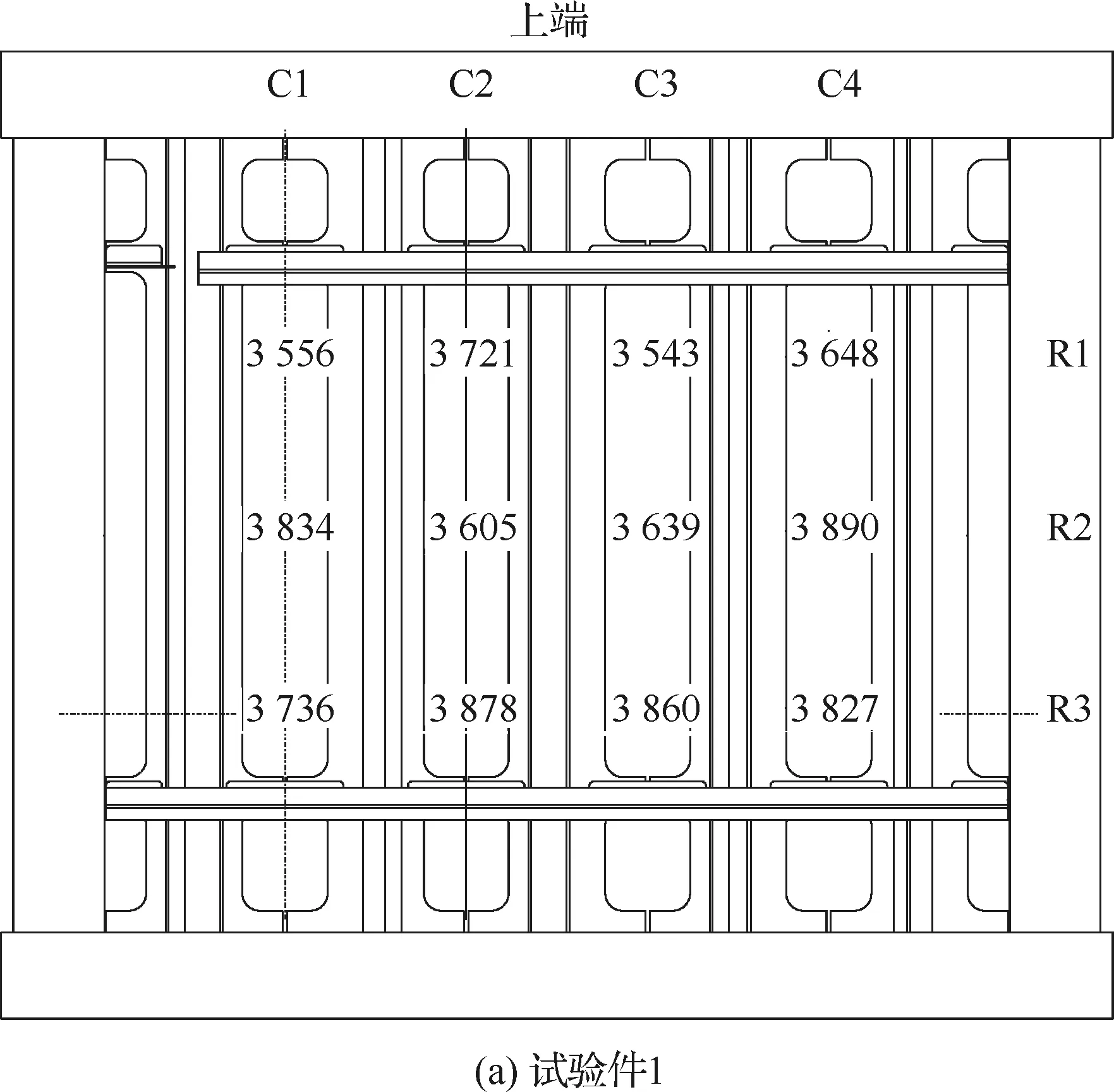
图7 300 kN载荷时3个试验件的剪切应变分布Fig.7 Shear strain distribution of three panels under load 300 kN

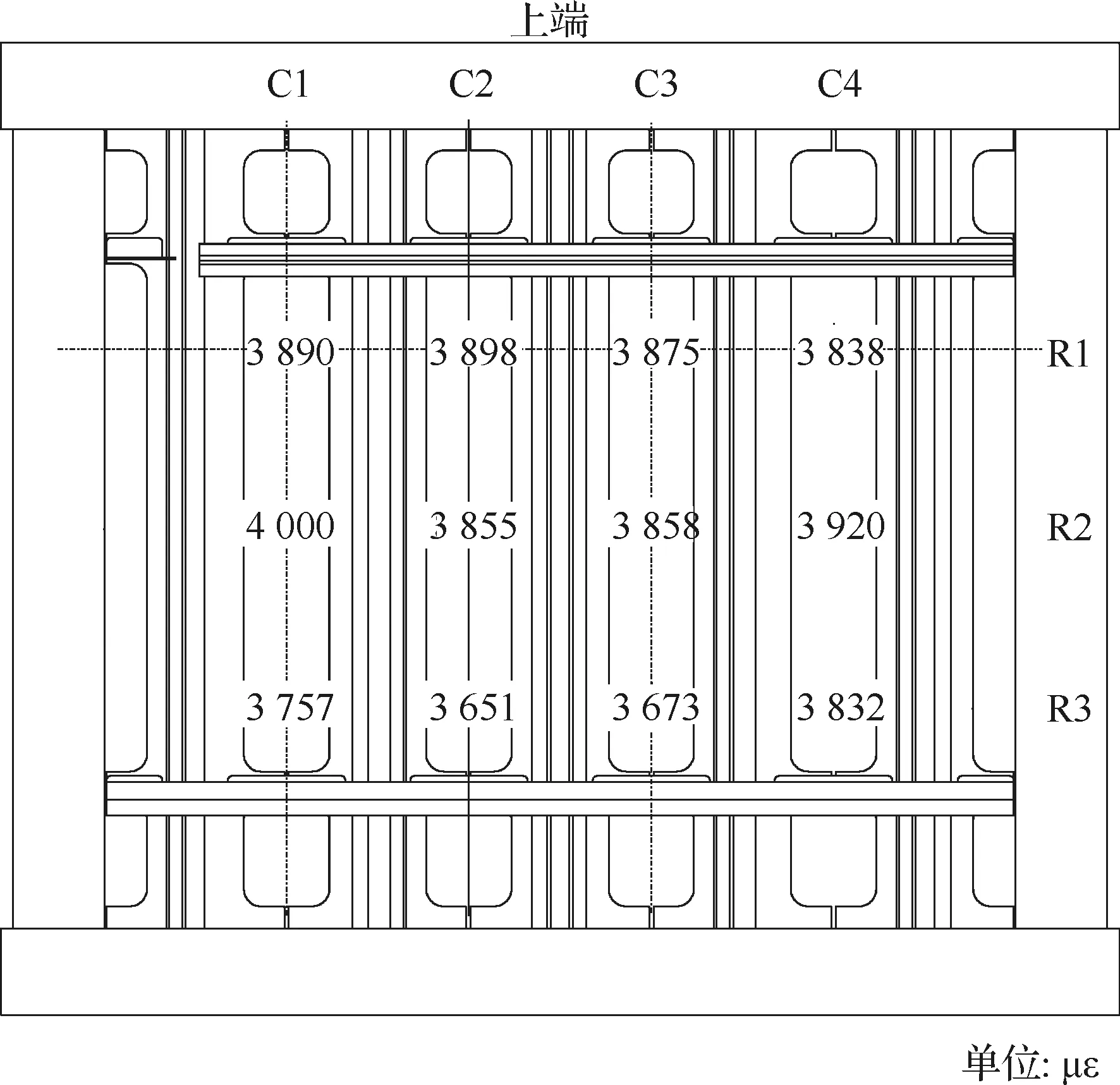
图8 300 kN载荷时有限元分析的剪切应变分布Fig.8 Shear strain distribution of finite element model under load 300 kN

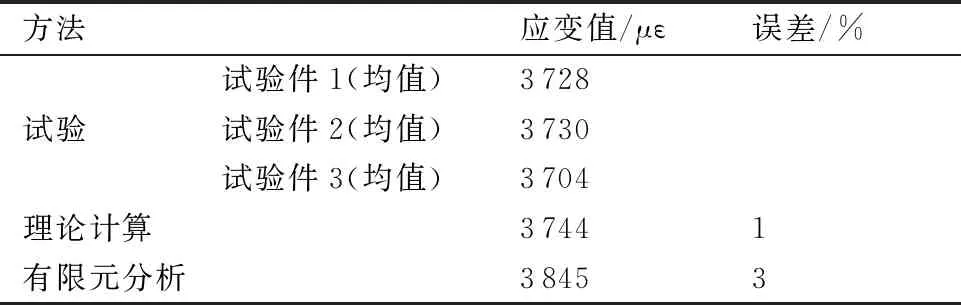
表3 300 kN载荷时剪切应变的试验与理论计算、有限元分析结果对比Table 3 Comparison of shear strain of test with theoretical calculation and finite element analysis results under load 300 kN

4.2 结构屈曲

试验调试完成，在保证试验件的状态正确、试验设备均处于正常状态下进行屈曲试验，试验现场依据采集的应变数据掌握试验件的状态，确保每一个试验件试验过程中屈曲。试验件(共3件)试验过程的载荷-剪切应变曲线如图9所示。由图可看出，相同截面试验件蒙皮内外侧剪切应变很接近，不同试验件的剪切应变分布差异较小，表明试验安装状态正确，试验控制稳定。

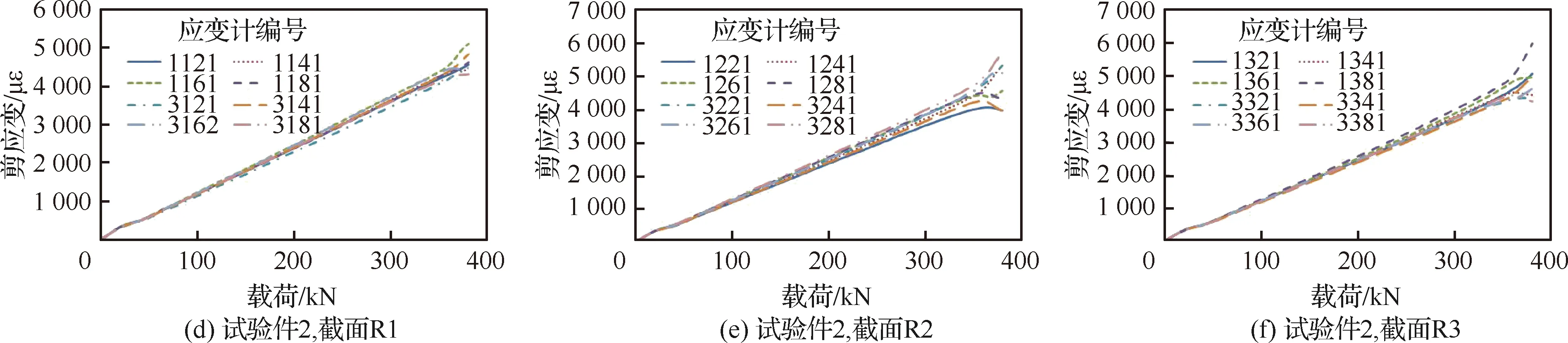
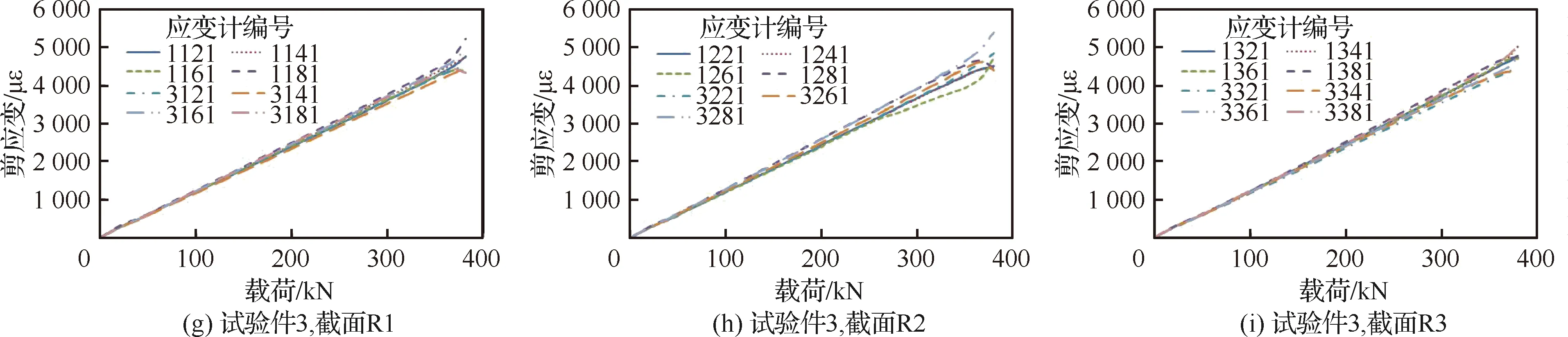
图9 3个试验件的载荷-应变曲线Fig.9 Load-strain curves of three panels

根据载荷-剪切应变曲线的首个拐点确定试验件的屈曲载荷，3件复合材料帽形加筋壁板试验件的屈曲载荷见表4，可看出，3件试验件的屈曲载荷很接近。

理论计算方法(式(9))和半经验公式方法(式(10))计算的剪切屈曲载荷见表5。蒙皮板条单元宽度的截取包括3种方法：长桁内间距、长桁外间距和凸缘中心距。长桁对蒙皮的支持是弹性支持，介于简支和固支之间，但理论计算方法和半经验公式计算法中只有理想边界条件：简支和固支，因此计算中对两类边界条件均分别进行了计算。表5中的误差为计算值相对试验值而算得的。

由表5可看出，用理论计算获得复合材料帽形加筋壁板的屈曲载荷，需选用蒙皮板条单元宽度为凸缘中心距，蒙皮边界条件为简支，由此而得到的屈曲载荷与试验载荷较接近，计算误差约5%。用半经验计算获得复合材料帽形加筋壁板的屈曲载荷，需选用蒙皮板条单元宽度为长桁外间距，蒙皮边界条件为固支，由此而计算的屈曲载荷与试验载荷较接近，计算误差小于5%。无论是理论计算还是半经验计算得到的蒙皮屈曲载荷，控制的参数主要是两个：蒙皮的宽度和边界条件，不同的计算方法选择的参数不一样，为了得到较准确的计算结果，需要选择两个合适的参数。

表4 3个试验件的剪切屈曲载荷Table 4 Shear buckling loads of three panels

用有限元特征值法计算的加筋壁板一阶屈曲模态见图10。可看出加筋壁板在各个长桁间均屈曲，其中第1长桁和第2长桁间有1个半波，第2、3长桁和第3、4长桁间有两个半波。得到的失稳载荷系数为435，对应的失稳载荷为435 kN。与试验结果对比可看出，采用特征值法求解加筋壁板的稳定性问题，能得到屈曲模态和屈曲载荷，但屈曲载荷高于试验结果，其误差达20%，偏危险。

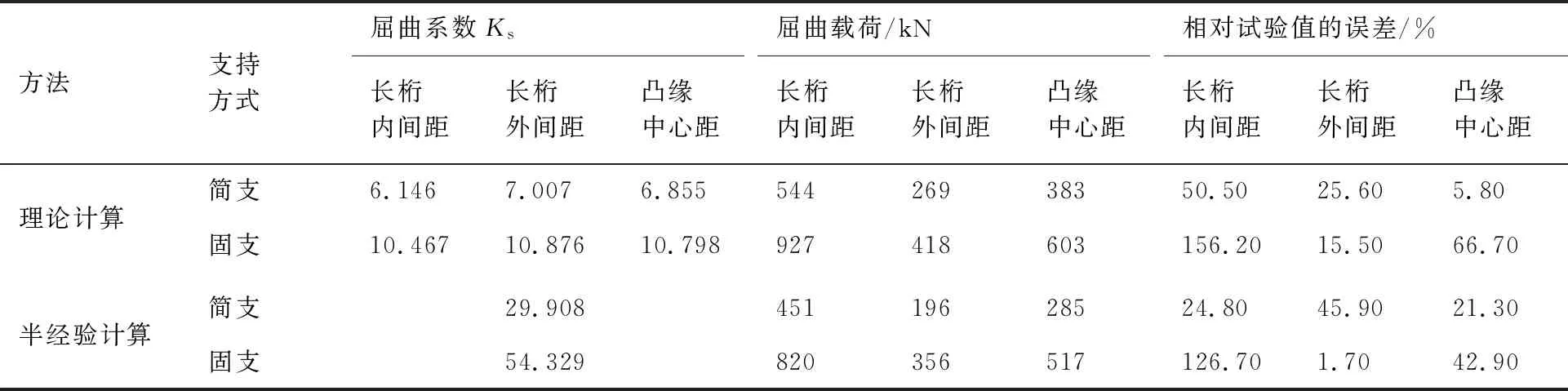
表5 理论计算和半经验计算得到的屈曲载荷Table 5 Buckling loads from theoretical and semi-experiential calculations

图10 加筋壁板一阶屈曲模态Fig.10 First buckling mode of stiffened panel

特征值法计算的屈曲载荷偏高的部分原因是未考虑结构的非线性和结构的缺陷。复合材料加筋壁板在制造过程中都会产生一定的缺陷，常见的缺陷有：几何初始缺陷(如蒙皮的不平整)、材料的不均匀(如纤维的弯折)、壁厚的不均匀(如树脂不均匀)，其中几何缺陷是主要的缺陷形式[33]，分析时通常将第1阶模态以几何缺陷的方法引入到模型中[34-35]。缺陷系数的定义为ζ=a/h(a为缺陷的幅值，h为蒙皮厚度)，分别取缺陷系数为0、3%、5%、8%、10%、20%进行计算，计算结果与试验结果的对比见图11(取图3第3、第4长桁中间位置的1361点作载荷-应变曲线的对比)。可看出，缺陷系数越高，载荷-应变曲线出现非线性(拐点载荷为屈曲载荷)就越早。当缺陷系数为8%时，计算得到的屈曲载荷(366 kN)与试验屈曲载荷(362 kN)接近；当缺陷系数小于8%时，计算的载荷-应变曲线与试验的载荷-应变曲线前段一致性较好，但计算得到的屈曲载荷均大于试验屈曲载荷；当缺陷系数为10%、20%时，计算的载荷-应变曲线较早进入非线性,与试验结果不一致。

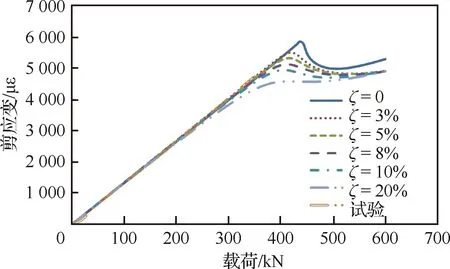
图11 不同缺陷系数下1361点的载荷-应变曲线Fig.11 Load-strain curves of point 1361 with different imperfection coefficients

5 结 论

1)根据线弹性理论得到的复合材料帽形加筋壁板的蒙皮应变分布与试验结果符合较好，较准确地反映了蒙皮的变形特征。

2)选择合适的边界条件和蒙皮的截取宽度，利用理论公式和半经验公式可较准确地计算出复合材料帽形加筋壁板的剪切屈曲载荷。

3)采用特征值计算出的复合材料帽形加筋壁板剪切屈曲载荷较试验屈曲载荷高；考虑结构的几何非线性及几何缺陷能有效地模拟复合材料帽形加筋壁板剪切屈曲过程。