激波风洞边界层转捩测量技术及应用
李强,江涛,陈苏宇,常雨,赵磊,张扣立
中国空气动力研究与发展中心 超高速空气动力研究所,绵阳 621000
高超声速边界层转捩现象是一个极其复杂的、具有强烈的非定常、非线性、对干扰极其敏感的三维过程,是一直没有得到解决的流体力学重大研究课题。由于边界层转捩问题的复杂性,至今尚未形成完整的转捩理论。高超声速边界层转捩用理论或计算方法难以准确预测。在工程应用上,模拟转捩流动大都依赖于由试验总结出的经验准则,基于线性稳定性理论(LST)的半经验eN方法[9-10]被认为是预测边界层转捩的一个有效方法。但该方法严重依赖于试验或经验,仅对二维或近似二维问题效果较好,对三维流动其应用结果并不令人满意。对于高超声速边界层转捩,如果没有试验数据和经验的帮助,则不能很好地进行基于理论的转捩及流动失稳预测。美国在20世纪70年代,开始研制能在大气层中做长距离飞行的高超声速飞行器,并同步开始重视高超声速边界层转捩预测研究。他们采用理论、计算、试验(包括风洞和飞行试验)高度结合的方法,积累了大量的结果[11-12]。
国内近几年开始进行一些高超声速边界层转捩研究工作,其中激波风洞作为高超声速气动热环境试验研究的主要地面模拟设备,模拟范围大、模拟能力强、模型尺度大、测量手段多,是研究高超声速边界层转捩的重要设备。激波风洞来流扰动较强、背景噪声较大,相比于静音环境,噪声环境会使得模型转捩雷诺数增大,转捩位置提前。2018年杨武兵等[13]采用测量风洞流场皮托压力脉动的方法,获得中国空气动力研究与发展中心∅2 m激波风洞(FD-14A)马赫数6(M6)流场风洞噪声水平大约为3%,M10流场风洞噪声水平大约为4.5%;在M5和M6运行条件下,国内几座用于转捩研究的风洞背景噪声均在1%~3%左右(包括中国航天空气动力技术研究院FD-07常规高超风洞、FD-20炮风洞/激波风洞,中国空气动力研究与发展中心FD-30∅1 m常规高超风洞)。文献[14-16]显示美国NASA兰利中心20InchM6风洞噪声水平大约为1%~1.5%,美国阿诺德工程中心(AEDC)9号风洞M10流场噪声水平大约为4.94%。因此包括∅2 m激波风洞(FD-14A)在内的国内高超声速风洞噪声水平与美国相关高超声速风洞噪声水平相当,都在百分之几量级。
激波风洞用于研究高超声速边界层转捩,需要发展适用的转捩测量技术。高超声速边界层转捩测试技术很多[13],都是依据边界层转捩过程中的热流、压力、密度、速度等物理特征的变化来判断转捩,目前适用于激波风洞高马赫数流场特点(气流速度高、气体密度低、毫秒量级试验时间)的高超声速边界层转捩测量技术主要有依据热流变化的点热流转捩测量技术和温敏热图转捩测量技术,依据压力变化的高频脉动压力测量技术和密度变化的高清晰度纹影测量技术等。本文发展了激波风洞原有的点热流和温敏热图测量技术,明确了转捩判断标准;以PCB132型高频脉动压力传感器为基础,发展了1 MHz量级的高频脉动压力测量系统及其数据处理分析方法;通过升级纹影仪和高速相机来提升纹影系统空间分辨率和时间分辨率的方式,发展了高清晰度纹影测量系统及其图像处理分析方法。
1 点热流转捩测量技术
点热流测量技术主要采用铂薄膜热流传感器来测量热流,其原理是以镀在绝缘基底上的铂膜作为测温电阻膜测量温度变化,利用热电模拟网络获得被测物体表面热流密度,其稳定性好、测量范围大、反应快、灵敏度高、精度高、重复性好、静态标定及使用简单可靠,是高超声速气动热环境风洞试验中的重要测量手段[17-18]。边界层从层流转捩成湍流后,会导致壁面热流升高,从而可以根据多只热流传感器测量的热流分布来判断转捩位置,一般认为热流开始升高的位置即为开始转捩位置。

图1 单个测点热流随时间变化典型曲线Fig.1 Typical curve of heat flux over time at a single measuring point
边界层流态与单个测点热流曲线特性存在一定关联。图1给出了某个热流传感器测量得到的热流随时间变化典型曲线,其中最左侧的热流突跃对应风洞气流到达传感器所在位置,气流开始对传感器传热。随后经历大约0.8 ms,模型周围形成稳定的绕流流场包括头激波和层流边界层的建立;层流边界层稳定流动大约2.6 ms,其中发生扰动线性增长等过程,但此时热流数值几乎稳定不变;随后该传感器位置处的层流边界层失稳转捩成湍流边界层,热流曲线上表现出来的就是图1中的热流突跃。最后传感器位置处变成湍流边界层,明显可见湍流边界层热流脉动比层流边界层强,这是湍流边界层中多尺度涡所引起的热流脉动;该传感器位置最终为湍流区,对于最终位于转捩区的传感器,其热流曲线不会出现热流突跃,会出现湍流斑导致的强烈脉动热流,对于最终位于层流区的传感器,其热流曲线既不会出现热流突跃也不会出现脉动热流,但层流、转捩、湍流3种状态之间没有绝对的界限,是一个渐进变化的过程。需要说明的是,风洞试验中模型及其传感器是静止的,边界层气流沿轴向从头部向底部流动,图1中单个测点热流随时间变化曲线,记录的是某时刻经过传感器的流体微团对传感器传导的热流;不同条件下热流传感器测得的热流曲线不完全一致,会根据马赫数、雷诺数、模型外形、边界层流态等因素而变化。
因此可以依据热流原始曲线判断传感器所处位置边界层流态。如图2所示,单点热流曲线与边界层流态对比,图2(a)热流曲线比较平滑,传感器位置处边界层在风洞有效试验时间范围内没有发生转捩,此处边界层最终为层流流态;图2(b)、图2(c)所示流体气动加热作用增强,热流曲线受湍流斑的影响出现不同程度的脉动现象,此处边界层发生转捩但未完成转捩,最终为转捩区;图2(d)边界层先经过层流边界层阶段,随后发生转捩,热流曲线突跃上升到一定值并保持相对稳定,此处边界层最终完成转捩为湍流。边界层流态变化引起流体气动加热程度发生变化,依托单点热流曲线时变特性及沿流向热流空间分布特性体现这一变化影响,这正是薄膜热流传感器判断转捩的依据。
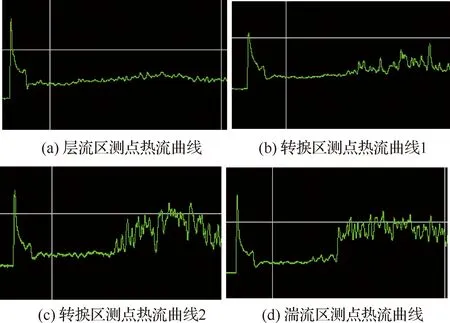
图2 单点热流曲线与边界层流态对比Fig.2 Comparison of heat flux curves and boundary layer flow state at single point
热电偶也是用于激波风洞等气动热环境试验的重要点热流测量传感器,其用于高超声速边界层转捩测量的方法与铂薄膜热流传感器基本相同。不同点主要是热电偶一般用于较高热流测量,其信噪比较低,因此在较低热流条件下无法通过单只传感器的热流曲线判断边界层转捩情况。但点热流转捩测量技术主要是依据热流沿流向空间分布特性来判断转捩,单点热流曲线时变特性用来辅助判断。
14日,两条显示为中国外交部部长王毅发布的推文截图开始广泛流传。截图显示,阐明中国外交部对瑞典警察粗暴对待中国公民态度时,第一条推文错将一处“瑞典”(Sweden)写成了“瑞士”(Swiss)。随后第二条推文就这一错误致歉。这一“失误”很快引来互联网上的另一波疯狂转发,并又给了一些网友“解构”瑞典事件的某种“合理想象”。
2 温敏热图转捩测量技术
温敏热图(TSP)测量技术[17-20]是一种大面积热流测量技术,它是利用温敏材料的光致发光特性随温度变化而变化的特点来进行模型表面温度分布测量的光学测量技术。其原理是在模型表面喷涂温敏磷光材料,以大功率紫外光源作为激发光源对模型进行照射,通过相机采集模型表面特定波段的发光强度,根据标定得到的光强与温度关系,获得试验时模型表面的温度分布,进而获得大面积热流分布。在激波风洞进行边界层转捩试验研究,边界层流态由层流转捩到湍流,流体的动量和能量输运能力增强,层流与湍流边界层传热效率的差异,体现在气动热上即是使得物面热流明显升高。对试验中得到的图像进行量化分析,得到模型表面大面积温度和热流分布,根据层流与湍流边界层传热效率的差异,对模型表面边界层转捩情况进行分析,得到转捩位置。
图3是在激波风洞开展的某平板边界层转捩试验研究中的温敏热图测量结果,定性展示平板模型表面边界层转捩情况,图中蓝色显示为低热流区域,边界层为层流流态;黄色为高热流区域,边界层为湍流流态。在平板上安装了6支热流传感器,对温敏热图试验结果进行对比验证。根据铂薄膜热流传感器单点热流曲线,可以看到前两个测点为层流状态,后4个测点为湍流状态,这与温敏热图的测量结果相一致。图4是某锥模型温敏热图测量结果,定性展示了锥模型表面边界层转捩情况,黄蓝色为低热流区,边界层是层流流态,红色为高热流区,边界层是湍流流态。

图3 平板模型温敏热图测量结果Fig.3 Test results of TSP on a flat model

图4 锥模型温敏热图测量结果Fig.4 Test result of TSP on a cone model
3 高频脉动压力测量技术
对于细长二维或轴对称外形的高超声速绕流流动,控制不稳定流动的典型模态是第2模态或Mack模态[21]。在边界层内,第2模态波传播速度与边界层外缘气流速度接近,波长近似为边界层厚度的两倍,第2模态波控制频率范围大致为100 kHz~1 MHz[22-23]。精确测量高频不稳定波特性具有挑战性,在很多冷流高超声速风洞试验中,表面齐平安装传感器的成功应用显示这一技术具有一定的应用前景。Fujii[24]第1次将快速响应压力传感器应用到1 MHz以下第2模态波测量,在激波风洞试验中获得成功。
传感器是实现高频压力测量的关键。为能够在脉冲风洞实现边界层转捩测量,需要压力传感器具有快速响应、高灵敏度、高固有频率等特性。快速响应特性满足激波风洞毫秒量级试验需求;高灵敏度特性能够有效捕捉微小压力脉动信号;高固有频率特性能够捕捉高频压力脉动信息。目前,能够满足需求的传感器只有PCB类型高频压电传感器,传统型号为132A31型,新型号为132B38型。国外风洞试验中大量应用PCB 132型压力传感器[22,14-15,22,25-28]测量得到了第2模态不稳定波。
PCB132A31型压力传感器固有频率超过1 MHz,目前激波风洞配套的数据采集处理系统采集频率可达3 MHz,采集精度优于0.1%。如图5所示,采用搭建的高频脉动压力测量系统获得锥模型表面高频脉动压力原始信号及功率谱密度结果,图中:t为时间、U为电压,这是PCB高频脉动压力传感器获得的原始信号,f为频率、PSD(Power Spectrum Density)为功率谱密度。


图5 PCB脉动压力测量结果及PSD结果Fig.5 Results of measurement and PSD of PCB pressure fluctuation
数采系统测量得到的是压力信号随时间变化曲线,对PCB压力传感器时域压力信号进行频谱变换,可得到压力信号频域曲线,进而分析压力信号的频谱特性。压力信号的能量随频率分布是频率域描述的一个重要部分,它提供了压力信号的频率结构。通常,通过计算PSD来分析,计算PSD通过Welch方法基于MATLAB集成函数实现。这一方法将时域压力信号分成多段,先计算每段的周期图,之后进行PSD平均处理,计算时需要设置数据重叠Overlap、计算周期图的加权窗Hamming window、快速傅里叶变换(FFT)长度等。如图5所示,对高频脉动压力时域信号进行功率谱分析,获得频域信号,该传感器获得的频域信号显示边界层不稳定波的主频为433.6 kHz。
4 高清晰度纹影显示技术
激波风洞等高超声速风洞均配备阴/纹影等流场显示系统,并应用此类技术开展常规高超声速绕流流场显示工作,得到飞行器绕流流场波系分布。对于边界层流动特性研究来说,需要针对高超声速细长、薄边界层流动区域进行显示,目前的纹影系统在空间和时间分辨率上,还达不到研究要求。为此,需要针对边界层流场特点、流动特性及转捩研究需要,对流场显示光学系统进行技术改造和性能提升。
高超声速边界层流场细长、薄,为实现边界层流场精细清晰显示,需要提高流场显示的空间分辨率。∅2 m激波风洞配备的纹影仪为满足全模型显示而设计,视场为∅400 mm,细节分辨不够清晰;光路为“Z”字型离轴反射式,像差较大、成像质量较低。在国外的研究工作中[22-23,29-31],所用视场通常为100~180 mm,专门对感兴趣区域进行显示。根据边界层流动显示要求,需要对边界层细长流动进行针对性显示,国外研究选择视场也是基于这一考虑,因此配置了一套∅200 mm的透射式纹影仪,主要由光源、狭缝、主镜、刀口、镜头、相机和支撑调整机构组成,光路如图6所示,L1为透镜1,L2为透镜2。配备的相机分辨率为1 024 pixel×1 024 pixel,空间分辨率可达到5 pixel/mm,主镜为双胶合透镜,可消除各种像差、提高清晰度。激波风洞流场密度相对较低,且流速较快,为捕捉高速流场特征,需提高时间分辨率,使用高速相机作为图像采集设备,配合高亮度光源,相机曝光时间为160 ns,拍摄频率为100 kHz,可避免图像拖影,捕获结构变化过程及分析频率。采用刀口自动定位系统进行纹影灵敏度的准确调整,挑选合适的灵敏度用于显示边界层结构。

图6 纹影仪光路图Fig.6 Optical sketch of schlieren system
采用上述升级的纹影系统在∅2 m激波风洞中拍摄获取的纹影图像如图7所示,给出了锥模型表面边界层4种典型的纹影图像。第1幅图像边界层为层流状态,由像素可求出边界层厚度,该边界层厚度是密度梯度厚度;第2幅图像边界层出现了明显的第2模态波即“绳状波”,这是由某种扰动在边界层中发展而成的不稳定波,由像素可求出其波长,将在下文中给出算例;第3幅图是第2模态波失稳猝发而成的湍流斑,湍流斑的出现意味着边界层开始转捩,在高速相机以10 μs间隔连贯拍摄的图像中,可以观察到第2模态波失稳变成湍流斑的过程;第4幅图像边界层为湍流状态,当湍流斑出现频率加快并前后连贯起来,则从高速相机连续图像中判定边界层完成转捩,图像中可以明显分辨湍流边界层比层流边界层厚,并且可见明显的扰动从湍流边界层传播开来。


图7 4种模态纹影图像Fig.7 Schlieren images of four modes
5 尖锥试验结果
5.1 尖锥试验条件
尖锥试验模型如图8所示,模型头部钝度为0.05 mm,理论尖点距模型底部800 mm,模型半锥角为7°。沿模型0°母线安装8个PCB高频脉动压力传感器,第1个传感器轴线与模型母线交点沿模型轴向距模型理论尖点125 mm,以后各传感器间距80 mm,8只PCB传感器与热流传感器位置关系如图9虚线标示。90°母线上,从x=125 mm(x是沿模型轴线至理论尖点的距离)位置处开始,间隔20 mm安装32个热流传感器。试验流场马赫数为10,单位雷诺数1.2×107m-1,静压为352 Pa,静温为44 K,气流速度为1 352 m/s。200 mm纹影仪视窗中尖锥模型母线范围约为x=293.8~467.5 mm(图9实线标示范围),该段母线中点x=380.7 mm。而4#PCB脉动压力传感器安装位置(x=365 mm)与该中点截面最接近,相同截面位置热流传感器为13#测点,因此下文中将选取4#PCB脉动压力传感器和13#热流传感器测量结果,与纹影结果及理论分析结果进行对比。

图8 7°尖锥模型Fig.8 7° half-angle cone model

图9 尖锥模型表面热流分布Fig.9 Heat flux distribution on cone model surface
5.2 热流测量结果
如图9所示,热流传感器测量获得尖锥模型表面沿母线的热流q分布情况,从图中可以明确在该流场条件下,尖锥模型表面边界层完成转捩。从热流分布图上看,第1个测点开始沿流向热流降低,此时边界层为层流流态;在x≈285 mm位置,边界层开始转捩,热流开始升高,一般认为热流开始升高的位置即为边界层转捩开始位置;随后在x≈485 mm位置,边界层转捩完成为完全湍流流态,热流开始逐渐降低,一般认为转捩区之后热流开始降低的位置即为边界层转捩完成位置。图10为尖锥模型表面边界层层流、转捩、湍流3种流态对应热流传感器的热流原始曲线对比。其中图9对应流向热流空间分布特性,图10对应单点热流时变特性。

图10 尖锥模型边界层不同流态对应测点热流原始曲线对比Fig.10 Comparison of original heat flux curves of measuring points corresponding to different boundary layer flow state of cone model
5.3 高频脉动压力测量结果
PCB高频脉动压力结果如图11所示,此为功率谱密度分析结果,从图中可以看出,PCB2~PCB5传感器测量得到明显的第2模态不稳定波频率,对应频率见表1,第2模态不稳定波频率顺流向降低,这是由边界层厚度增加而导致。从图9中可以看出,PCB2~PCB5位置边界层为层流与转捩状态,PCB6~PCB8位置边界层已经完全转捩成湍流状态,各种频率波的能量已经分散,不存在频率能量集中的峰值。将试验结果与理论计算进行比较,采用eN方法获得了不同频率扰动的N值分布(如图11所示),由N值分布确定了PCB传感器所在位置处的主导扰动频率如表1所示,线性稳定性理论分析获得的第2模态波频率与试验测量结果基本相吻合,除2#PCB传感器偏差较大,其余传感器位置理论结果与试验测量结果偏差在6%以内。

图11 脉动压力功率谱密度(实线)与线性稳定性理论分析N值(虚线)对比Fig.11 PSD of pressure fluctuations(solid line)and comparisons with N factor(dotted line)from LST computation

表1 第2模态波PCB传感器测量频率与线性稳定性理论频率对比Table 1 The second mode wave frequency measured by PCB sensors and comparison with LST computation
5.4 高清晰度纹影测量结果
图7已经给出高清晰度纹影技术测量获得的高超声速边界层转捩过程中的典型图像。图12给出了随机时刻4张边界层内第2模态波(绳状波)原始纹影图像,每张图像都有第2模态波存在,其中图12(a)距离气流到达13#热流测点的时间约为3.34 ms。对纹影图像进行后处理[32],在边界层内提取一条平行于壁面直线的灰度分布(Bbicubic插值法),以无流场(真空)的纹影图像作为参考值做平均化处理以消除边缘虚化的影响,然后对其做PSD分析,自变量为空间频率fsp,可以分析边界层内扰动的空间分布特性。图13对比了4张纹影图像相应的PSD曲线,结果显示,前两张图像对应的PSD均在fsp=0.214 mm-1附近存在峰值,即对应第2模态波的波长λ=4.67 mm;后两张图像对应的PSD均在fsp=0.248 mm-1附近存在峰值,即对应第2模态波的波长λ=4.03 mm。
随机选取一些纹影图像进行处理,发现第2模态波波长数值是随机变化的,按照试验数据测量经验,猜测第2模态波波长会围绕某一特定数值来回振荡分布。因此选取有效试验时间范围内192张连续纹影图像进行批量处理,获得波数fsp随时间的变化曲线如图14所示。图15给出了相应波数的频次直方图分布,其基本上呈现单峰分布,峰值波数fsp=0.237 mm-1,即波长为λ=4.22 mm。图14和图15说明本次试验测量获得的第2模态波波长数值,围绕λ=4.22 mm这一特定波长数值呈现振荡的单峰分布状态,这主要是由于风洞来流参数振荡和测量误差所导致,但该现象符合试验测量数据特征。将线性稳定性理论分析方法给出的第2模态波波长与纹影图像数据处理得到的波长进行比较,如5.1节所述,采用线性稳定性理论方法求得x=365 mm处第2模态波波长为4.40 mm,而纹影图像得到第2模态波峰值波长为4.22 mm,理论分析结果与试验结果基本相吻合,仅偏差4.3%。

图12 第2模态波纹影图像Fig.12 Schlieren images of the second mode waves

图13 边界层流向截线灰度PSD曲线Fig.13 Gray value PSD curves on a streamwise line across boundary layer

图14 有效试验时间内第2模态波特征波数随时间变化Fig.14 Variation of characteristic wavenumber of the second mode wave during effective test time with time

图15 有效试验时间内第2模态波特征波数直方图Fig.15 Histogram of characteristic wavenumber of the second mode wave during effective test time
5.5 不同测量技术试验结果对比
对于热流测量结果与高清晰度纹影测量结果的对比,与第2节类似,纹影图像完整记录风洞气流到达模型、模型稳定流场建立、边界层层流流动、边界层失稳猝发湍流斑、边界层转捩为湍流等过程。图12是层流状态下边界层中第2模态波纹影图像,当边界层继续发展(前提条件是雷诺数足够高),边界层开始失稳猝发湍流斑,图12中后两张纹影图像视图下游出口处已经出现湍流斑。图16是x=365 mm位置13#热流传感器的热流原始信号,左边热流突跃即风洞气流到达传感器时刻,第1条黄色标线对应图12中第1张纹影图像时刻(3.34 ms),此时边界层是层流流态,热流相对较低;第2条绿色标线对应图17纹影图像时刻(5.80 ms),此时边界层为转捩区,热流出现强烈脉动情况,这是纹影图中出现的湍流斑所导致的现象。图17中纹影视窗上下游各有一个湍流斑,而中间区域存在第2模态波,说明湍流斑的猝发存在一定的偶然性和随机性。湍流斑不是固定不动的,它会随着气流向下游移动,因此当湍流斑扫过热流传感器时,传感器测量得到的热流曲线上出现尖峰脉冲。需要说明的是,本次试验热流传感器安装在下缘母线上,纹影图像记录的是上缘母线,两者周向角为180°,虽然尖锥模型迎角为0°,但由于湍流斑猝发的偶然性和随机性,热流信号与纹影图像在时间序列上并不完全对应。

图16 13#热流传感器(x=365 mm)热流原始信号Fig.16 Heat flux original signal of 13# heat flux sensor (x=365 mm)

图17 t=5.80 ms纹影图像Fig.17 Schlieren image at t=5.80 ms
5.3节中已经说明了PCB传感器测量结果与边界层流态的关系,这里对处于转捩区的PCB传感器测量结果进一步说明。把高频脉动压力测量结果与热流测量结果和高清晰度纹影测量结果进行对比,从图16、图17中看出,在湍流斑出现的间歇期存在局部短时层流状态,其中存在第2模态波,这导致转捩区的PCB传感器能够测量得到第2模态波频谱特性。
接下来对比高清晰度纹影测量结果与高频脉动压力测量结果。选取3.64 ms时刻的纹影图像,按照上述方法对第2模态波图像处理得波长即峰值波长为4.22 mm。对t=3.64 ms和3.65 ms连续两张纹影图像采用互相关分析方法进行处理,处理方法如下:
(1)
式中:p、q分别为两张很短的时间间隔内纹影图像对应点的灰度值;k、l为对应点的位移分量。然后归一化,
(2)

6 结 论
根据高超声速边界层转捩过程中热流、压力、密度等参数变化特点,对激波风洞已有的试验测量技术进行适应性改造和升级,发展了点热流、温敏热图、高频脉动压力、高清晰度纹影等适用于激波风洞的高超声速边界层转捩测量技术。并针对头部钝度0.05 mm的半锥角7°尖锥模型,在中国空气动力研究与发展中心(FD-14A)马赫数10、单位雷诺数1.2×107/m的流场条件下开展了边界层转捩试验,采用点热流、高频脉动压力、高清晰度纹影3种转捩测量技术同时进行测量,获得了较好的试验结果。
通过点热流转捩测量技术获得了转捩开始、完成位置等尖锥边界层转捩情况;通过高频脉动压力测量技术获得了尖锥边界层转捩频谱特性,并获得了第2模态波主导频率;通过高清晰度纹影技术获得了尖锥边界层转捩过程中出现的第2模态波、湍流斑等结构的清晰纹影图像,并记录了相关边界层结构生成、转化过程,为分析高超声速边界层转捩特性提供了直观和动态图像。
不同测量技术试验结果对比表明,热流传感器记录的热流脉动情况与纹影图像中湍流斑的出现有相关性;热流测量获得的边界层转捩情况与脉动压力反映的边界层流态特性相吻合;采用空间尺度快速傅里叶变换方法对纹影图像边界层中灰度值进行分析获得第2模态波波长,采用互相关方法对纹影图像中第2模态波移动速度进行分析,通过波长、波速、频率关系式获得第2模态波频率,与相对应位置PCB传感器测量获得的第2模态波主导频率相吻合。另外通过线性稳定性理论分析获得的第2模态波频率与PCB传感器测量的频率基本相吻合,线性稳定性理论分析获得的第2模态波波长与纹影图像中记录波长相吻合。

