基于线性稳定性分析的翼尖涡摇摆机制
邱思逸,程泽鹏,向阳,刘洪
上海交通大学 航空航天学院,上海 200240
翼尖涡是飞机尾迹中一种典型的大尺度涡结构,大型客机的翼尖涡可以在100倍机翼弦长的尾迹区域内维持,从而对后续飞机的安全飞行产生威胁,限制了机场起降频率[1]。此外,由翼尖涡诱导下洗产生的诱导阻力是飞机阻力的主要来源之一[2]。Gerz等在2002年总结提出了控制飞机尾迹涡影响的两大策略:① 减弱翼尖涡强度;② 使翼尖涡快速衰减[1]。目前通过加装翼梢小翼等流动控制方法可以有效地减少翼尖涡强度,然而针对第2种策略却缺乏有效的流动控制原理及方法。事实上,已有研究表明,涡的破碎和耗散与其不稳定性特征密切相关[3],而翼尖涡在演化过程中包含明显的不稳定性特征,其在一定条件下表现为低频的摇摆运动(Vortex Wandering)[4-5],这种现象目前被认为主要由翼尖涡内在的不稳定性导致[6],且在整个尾迹区内其不稳定性存在主导频率[7-9]。通过施加与此频率相匹配的流动控制,或者利用涡系间的相互作用,增大翼尖涡不稳定性的放大率[1,10],使流动提前进入由短波或长波不稳定性[11]主导的快速耗散状态,可以实现翼尖涡的快速衰减;此外,已有研究者利用流动不稳定性的响应频率实现了有效的非定常推进[12],表明不稳定性是一种值得深入研究并加以利用的流动内在特性。因此,研究翼尖涡摇摆运动,可以明确不稳定性特征对翼尖涡流动的影响机制;在此基础上,有助于进一步利用流动不稳定性的频率或模态特征激发翼尖涡发生失稳,通过非定常的流动控制策略对翼尖涡实施控制。
摇摆运动是翼尖涡在其不稳定性特征作用下所呈现的具体现象之一,表现为翼尖涡在流向截面内拟序的低频振荡,最初由Baker等在水槽试验中发现[4]。由于摇摆运动使翼尖涡物理参数的测量与求解产生误差,消除摇摆运动对实际流场测量的影响以及探寻其内在的物理机制一直是研究者的重点关注所在。Devenport等首次对翼尖涡摇摆现象予以修正,通过联合概率密度函数近似表征瞬时涡核位置分布,并使用反卷积修正法消除翼尖涡摇摆对测量的影响,在此基础上得到了清晰的远场翼尖涡湍流相干结构[5];同时在较小斯特劳哈尔数的条件下,观察到了翼尖涡摇摆的各向异性现象。对于粒子图像测速(PIV)试验测量得到的翼尖涡流场,可以使用涡核重新定位的方法进行修正[6,13]。Deem等比较了上述两种方法对翼尖涡摇摆的修正效果,结果表明瞬时涡核位置分布满足高斯分布,且摇摆运动表现出各向异性的特点[14]。试验研究发现,翼尖涡摇摆幅值随流向增长[13],且随迎角[15-16]与涡强度[13]的增大而减小。薛栋使用单点谱分析和动力学模态分解技术得到在雷诺数103量级下,翼尖涡摇摆的主频率约为1 Hz[8],也表明了摇摆运动存在主导频率。在此基础上,Edstrand等比较了理论Q涡模型的线性稳定性分析结果和翼尖涡试验数据的本征正交分解模态,证明了翼尖涡摇摆来源于其内在不稳定性特征[6]。由此可见,对于翼尖涡摇摆现象已经有相对成熟的修正方法,但是在稳定性作为翼尖涡摇摆主要原因的基础上,翼尖涡摇摆现象自身的演化规律和机理仍没有明确的阐释,稳定性对翼尖涡流动具体的影响机制也需要进一步分析。
通过线性稳定性分析(Linear Stability Analysis,LSA)可以计算得到翼尖涡流动的不稳定性放大率、扰动频率和扰动模态,从而对翼尖涡的不稳定性特征进行定量的分析研究[17-20]。最初,一些研究者使用线性稳定性分析对不同翼尖涡理论模型的稳定性进行了参数化的研究。Mayer和Fabre等使用线性稳定性分析对翼尖涡的理论Batchelor涡模型[21]的研究结果表明,翼尖涡的不稳定性受其旋拧度(Swirl Parameter)、扰动周向波数n、雷诺数Re和黏性影响,增大旋拧度对翼尖涡具有稳定作用,而增大雷诺数会减弱旋拧度的稳定效果[22-23]。同时,研究发现扰动周向波数n=-1的螺旋模态是最不稳定的[22-24],不稳定性随周向波数n增加而递减;并且有黏流动相比无黏流动更稳定[24]。然而以上研究都是基于翼尖涡理论模型,较难反映实际流动的稳定性。因此,有研究者对试验数据拟合的流动解析解或直接数值模拟(DNS)结果进行线性稳定性分析,从而得到更接近真实的流动稳定性特征。Oberleithner等对试验测得的旋转射流的线性稳定性分析结果表明,这种流动存在一种自激励的全局模态,且该模态存在主导频率,并通过LSA和POD分析分别重构了这种流动的三维扰动速度场[7];Edstrand等使用Bi-Global LSA分析了DNS(Re=1 000)得到的近场尾迹区的翼尖涡流动,探讨了后缘尾迹对翼尖涡稳定性的影响[25]。然而,目前对于翼尖涡不稳定性放大率、扰动频率等不稳定性参数随流向的变化过程缺乏明确的定量化研究,在一定程度上限制了对于不稳定性对翼尖涡摇摆运动作用机制更深入的理解。
综上所述,对于翼尖涡摇摆现象的研究主要集中于对其进行修正以获取更准确的翼尖涡流场;虽然稳定性作为翼尖涡摇摆的内在原因已得到初步证实,但是翼尖涡摇摆现象自身的演化规律和机理尚需更深入的研究,其演化特性与不稳定性的关系也仍需进一步明确,从而进一步阐释不稳定性特征对翼尖涡流动的作用机制。因此,本文通过SPIV(Stereo Particle Image Velocimetry)试验技术测量不同雷诺数、迎角下的翼尖涡流场,得到了翼尖涡摇摆运动的特征及演化过程;进一步地,通过线性稳定性分析研究了雷诺数和迎角对翼尖涡不稳定性的影响,并求解其不稳定性随流向的演化过程和扰动模态。在此基础上,分析了翼尖涡的不稳定性特征与摇摆运动的关系,阐释了翼尖涡摇摆运动的产生机制,从而为这类流动的非定常流控策略提供参考。
1 试验方法与后处理计算
1.1 SPIV试验方法
试验在低速回流式风洞中进行,最大风速为70 m/s,试验段尺寸为1.2 m×0.9 m。收缩段前安装蜂窝网以降低试验段的湍流度,试验中的湍流度为0.2%。使用NACA0015等直翼产生翼尖涡,机翼弦长c= 0.203 m,展弦比AR=5。试验过程中,机翼安装在一个与风洞内壁面底部固定的转盘上以实现迎角的调节。测试迎角为α=4°,8°,10°;来流速度U∞=15,20,25 m/s,对应基于弦长c的雷诺数分别为Re=2.1×105,2.8×105,3.5×105;尾迹区内翼尖涡流场的测量范围x/c=0.6~6.0,等距离分布共计10个截面,其中x为流向坐标。
翼尖涡流场通过SPIV获得,通过大小为1~5 μm 的乙二醇小油滴对流动进行示踪。激光光源选用Nd:YAG双脉冲激光发射器,对流场进行显示。试验所用激光的双脉冲能量为2×380 mJ,双脉冲频率为1 Hz,激光波长为532 nm,两次脉冲间隔为10 μs,片光源的厚度为2 mm并垂直于来流方向。使用2台型号为Imager-Pco的高分辨率CCD相机对激光片光源照射的流场截面进行拍摄,相机夹角为90°,如图1所示。试验中图像采集的分辨率为2 048 pixel×2 048 pixel,采样频率同步为1 Hz,通过532 nm波长带通滤光镜来提高图像信噪比。为了得到翼尖尾迹区内不同截面的翼尖涡结构,可通过导光臂调节激光器所发射片光源在流向的位置。对每个截面采集200 s流场数据,并通过TSI INSIGHT 4G软件对图像进行配对和解算,其解调范围为24 pixel×24 pixel,有效重叠率为50%,得到翼尖涡流场在x、y、z这3个 方向的速度,并计算得到涡量场。
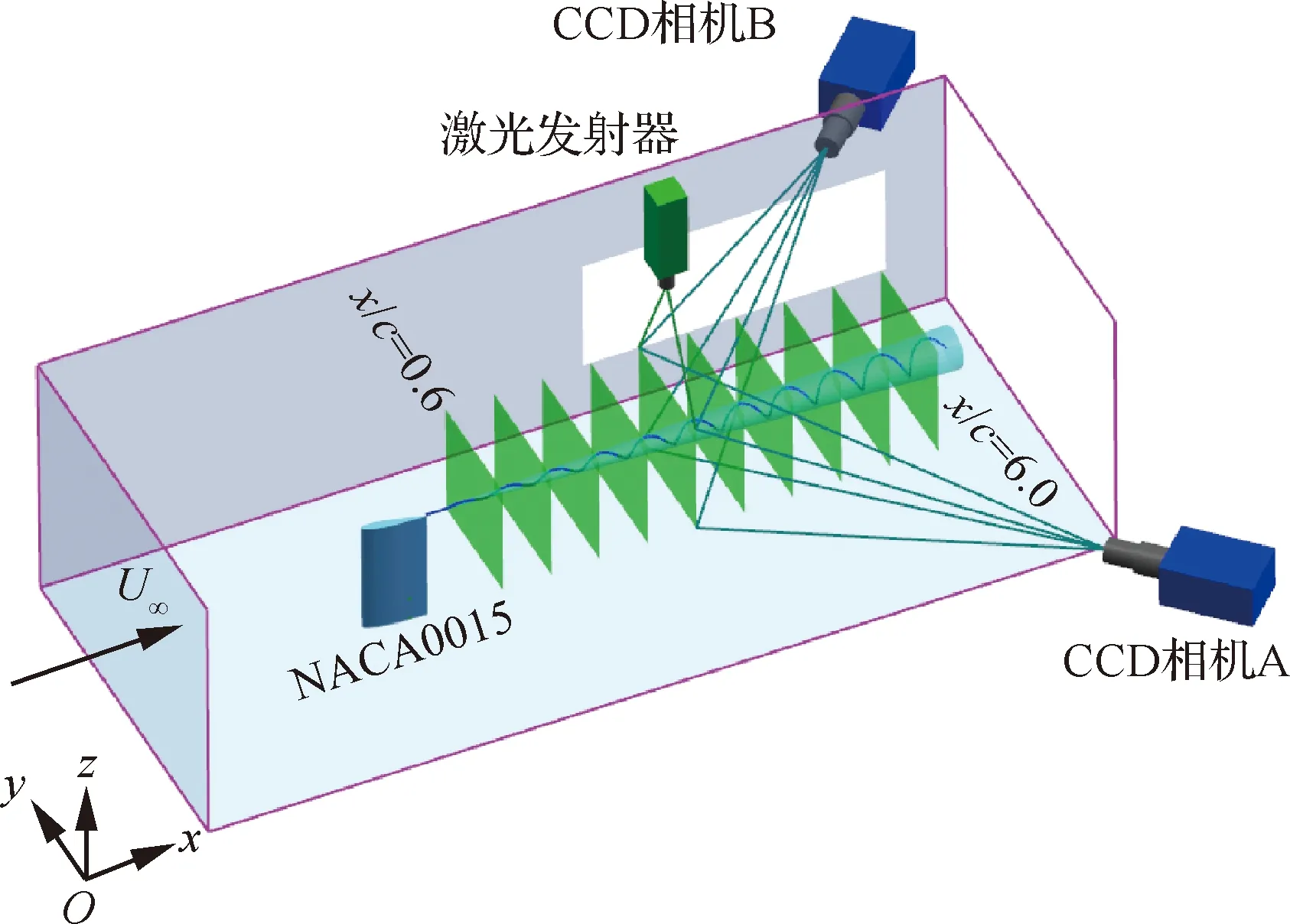
图1 SPIV试验设置示意图Fig.1 Schematic of SPIV experimental setup
1.2 试验后处理计算
通过瞬时涡核位置表征翼尖涡在摇摆过程中各个时刻的位置。由于翼尖涡摇摆运动的影响,以切向和径向速度最小位置确定的涡核位置不准确,因此本研究中以涡量一阶原点矩的方法确定翼尖涡的瞬时涡核位置:
(1)
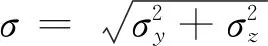
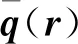
(2)

2 翼尖涡摇摆特征
计算各截面的SPIV流场瞬时涡核位置,获得翼尖涡在不同截面的瞬时涡核分布,如图2所示。由图2可知,α=8°,U∞=25 m/s条件下近场(x/c= 1.2)瞬时涡核的分布近似各向同性,随着翼尖涡向下游传输,摇摆幅值逐渐放大,且涡核分布逐渐呈现出各向异性特征,相关系数e也反映了各向异性特征随流向逐渐增强的趋势。比较试验测得的瞬时涡核在y、z方向的分布与根据平均涡核位置和σy、σz确定的高斯分布,可见两者精确符合。高斯分布描述的瞬时涡核分布定量地反映了以上翼尖涡摇摆规律,即摇摆幅值随流向逐渐增大,并且σy>σz。
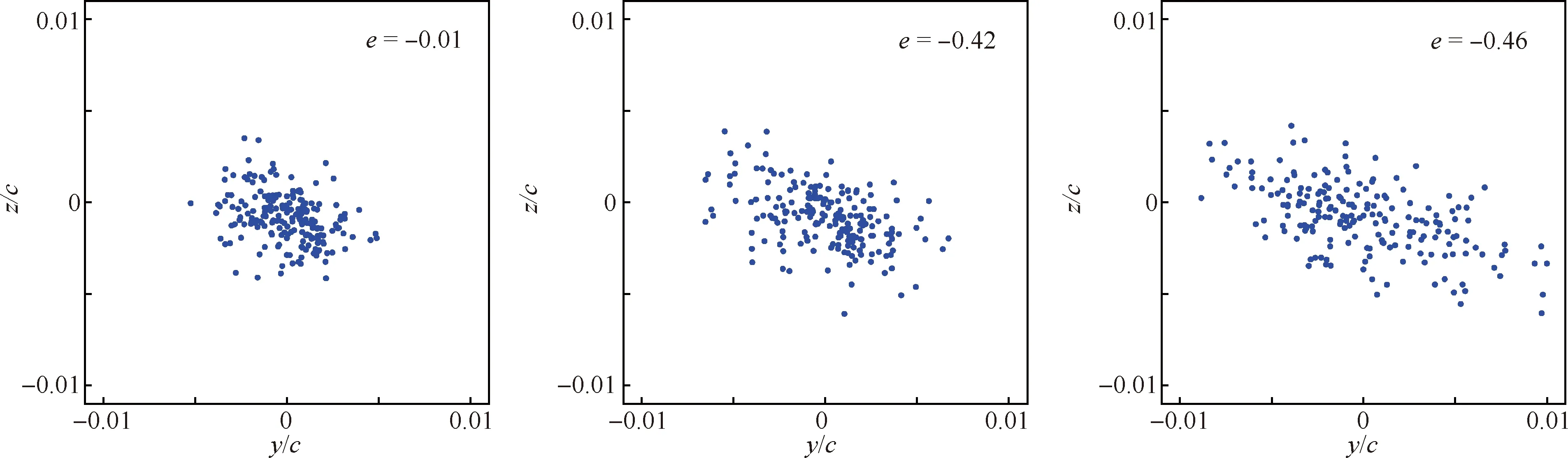

图2 α=8°,U∞ = 25 m/s工况下的瞬时涡核分布和其概率密度函数(PDF)分布Fig.2 Distribution of instant vortex core at α=8°,U∞ = 25 m/s and corresponding probability density function distribution
2.1 翼尖涡摇摆幅值变化
计算各工况下翼尖涡摇摆幅值沿流向x的变化,使用当量涡核半径rc对其无量纲化,如图3所示,可以发现摇摆幅值在各种条件下均随流向有逐渐放大的趋势。此外,4°迎角下翼尖涡摇摆幅值显著大于8°和10°迎角;并且8°和10°迎角下摇摆幅值随流向增长相对于4°迎角明显更为迅速。造成这种现象的原因是不同流动状态的翼尖涡稳定性存在差异,外界扰动在4°迎角条件下不易发展,因此摇摆幅值增长较为缓慢,进一步的定量化解释可参见第4节中的线性稳定性分析结果。比较雷诺数对翼尖涡摇摆幅值的影响,可以发现试验中在Re=2.1×105,2.8×105,3.5×105条件下各迎角的翼尖涡摇摆幅值基本处在同一范围。

图3 翼尖涡摇摆幅值σ随流向x的演化Fig.3 Streamwise evolution of wingtip vortex wandering amplitude σ along x
需要指出的是,翼尖涡摇摆幅值虽然沿流向总体表现出放大趋势,但其过程中可能存在波动,如在Re=2.8×105和Re=3.5×105条件下,x/c=2.4截面的翼尖涡摇摆半径存在局部减小的情况。因此,取单一截面研究翼尖涡摇摆幅值随迎角、雷诺数变化得到的结果可能不准确[26],应当从翼尖涡在尾迹区内演化的整体角度对翼尖涡摇摆运动进行研究。
2.2 翼尖涡瞬时涡核分布
在2.1节中已对翼尖涡摇摆的特征及其摇摆幅值随流向演化进行了阐述,为了更直观地描述翼尖涡摇摆运动随流向的变化规律,并显示翼尖涡随流向运动轨迹,计算x/c= 1.2,3.6,6.0的瞬时涡核分布在各迎角和来流速度条件下的联合概率密度(JPDF)分布。图4清晰地显示了涡核由近场的集中分布,沿流向逐渐发展为十分离散的分布,并且在机翼法向摇摆幅值更大,即具有明显的各向异性特征,摇摆运动的方向与Iungo等的试验结果[16]一致。
图5显示了各个雷诺数和迎角下涡核位置联合概率密度分布沿流向的演化过程。从图5(a)可以观察到,在4°迎角下翼尖涡摇摆的幅度基本随流向保持一致,表现为较缓慢的增长;而在8°迎角和10°迎角条件下,翼尖涡摇摆运动幅值显著增大。此外,翼尖涡在沿流向演化过程中逐渐表现出明显的各向异性,并且在大迎角条件下更为显著。由图5(b)和图5(c)中的x/c=6.0截面可观察到,在8°和10°迎角下机翼法向的摇摆运动明显相比于展向的运动更为剧烈,而在4°迎角下这种各向异性并不十分明显。
综上所述,试验结果表明,翼尖涡在各试验工况下均存在摇摆运动,其摇摆幅值随迎角增大而减小;但是在8°与10°迎角条件下,摇摆幅值随流向x的增长率相比于4°则明显更大,即在大迎角条件下,摇摆幅值的流向增长率更大;同时,翼尖涡摇摆的各向异性特征随流向x方向逐渐增强。
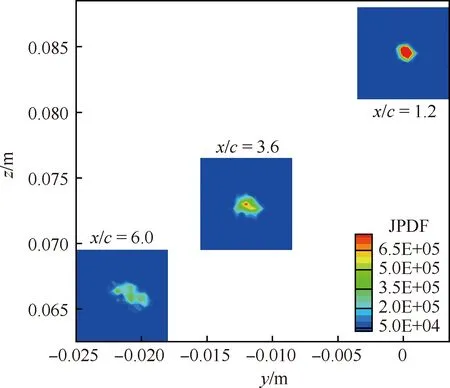
图4 涡核位置联合概率密度分布(α= 10°,U∞ = 25 m/s)Fig.4 JPDF distribution of vortex core at α = 10°,U∞ = 25 m/s
3 线性稳定性分析方法
3.1 扰动方程
为了对翼尖涡摇摆产生机制进行更深入的研究,使用线性稳定性分析求解翼尖涡的不稳定性演化过程和不稳定模态。通过求解线性化的小扰动Navier-Stokes方程,可以定量地得到反映流动不稳定性特征的相应参数。本研究中使用柱坐标系(r,θ,x)下的扰动方程形式,其中各瞬时流动变量可写为
q=[ur,uθ,ux,p]T
(3)
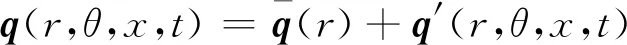
(4)
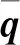
q′(r,θ,x,t)=[ur′,uθ′,ux′,p′]T=
(5)
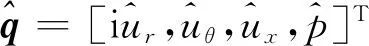
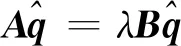
(6)
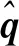



图5 不同雷诺数和迎角条件下涡核联合概率密度分布随流向演化(云图范围为[0.5×105,7.5×105])Fig.5 Streamwise evolution of joint probability density distribution of vortex cores at different Re and α (Contour range:[0.5×105,7.5×105])
3.2 程序验证
在求解试验测量的翼尖涡流场的稳定性特征之前,分别通过3个时间不稳定性算例和2个空间不稳定性算例对本文所使用的求解流动稳定性的方法和程序的准确性予以验证,算例包含圆管中的Poiseuille流和Batchelor涡等典型流动。
3.2.1 时间不稳定性
对圆管中Poiseuille流分别计算了Re=200和Re=2 200条件下的时间不稳定性,周向波数n=1,流向波数β= 1;在此基础上对角速度Ω为0.1的管壁旋转运动予以验证,计算条件为:Re=100,β=0.5,1.0,n=0,Ω、β、n均为无量纲量。计算结果与文献比较如表1和表2所示。从表1和表2中的对比结果可以发现,文中方法对Poiseuille流的时间不稳定模态的特征值能够实现准确求解。
进一步计算Re=141.4,β= 1.34条件下旋拧度在0.1~1.4范围内的尾迹涡稳定性,其中包含两个较不稳定的模态,与文献[20]比较如图6所示。从图中可以看出对于一阶不稳定模态和二阶不稳定模态,本文中使用的方法与文献结果符合较好。

表1 圆管Poiseuille流时间不稳定性结果(n = 1,β = 1)与文献[20]比较Table 1 Comparison of temporal instability results of Poiseuille flow (n=1,β=1)in a pipe with Ref.[20]

表2 旋转圆管Poiseuille流时间不稳定性结果与文献[20]比较(Re=100,n=0)Table 2 Comparison of temporal instability result of Poiseuille flow in a rotating pipe with Ref.[20](Re=100,n=0)
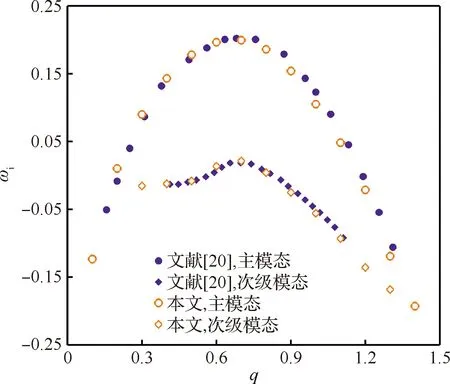
图6 尾迹涡时间不稳定性与文献[20]比较Fig.6 Comparison of temporal instability of trailing vortex with Ref.[20]
3.2.2 空间不稳定性
对圆管中的Poiseuille流进行空间不稳定性计算,计算条件为:雷诺数Re=10 000,频率ω= 0.5,周向波数n分别为0和1,与文献结果比较如表3所示。进一步计算Batchelor涡的空间不稳定性以对程序进行验证,条件分别为Re=667、n=-1、ω=-0.15,旋拧度为0.7和Re=108、n=-1、ω=-2.75,旋拧度为3,与文献结果比较如表4所示。
表3和表4的结果表明,研究使用的方法可以精确计算求解大范围雷诺数条件下的Poiseuille流和Batchelor涡的空间不稳定性,为之后的研究奠定了基础。

表3 圆管Poiseuille流空间不稳定性结果与文献[20]比较Table 3 Comparison of spatial instability results of Poiseuille flow in a pipe with Ref.[20]

表4 Batchelor涡空间不稳定性结果与文献[20]比较Table 4 Comparison of spatial instability result of Batchelor vortex with Ref.[20]
4 翼尖涡不稳定性对摇摆运动作用机制
4.1 翼尖涡线性稳定性分析
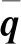
由于流场的扰动是不同频率、波数的扰动分量的叠加[12],因此需要寻找在何种频率、波数下,由特征值谱得到的扰动主模态随空间或时间的放大率最大,由此确定翼尖涡的空间与时间不稳定性。图8显示了x/c=4.8,α=10°,U∞=25 m/s条件下,不同扰动波数β的扰动主模态的时间放大率ωi关于β的变化曲线。ωi-β曲线的每一个点均反映了时间不稳定性特征值谱的扰动主模态在对应的扰动波数β下的时间放大率,例如图8的插图即为β=0.3的时间不稳定性特征值谱,扰动主模态的特征值由方框标出。由ωi-β曲线的极值点可得,波数β=0.295的扰动主模态的时间放大率最大,因此该极值点所对应的就是该截面与工况下翼尖涡的时间不稳定性模态,放大率为ωi= 5.71×10-5。对于空间不稳定性分析,计算具有不同频率ω的扰动主模态的空间放大率-βi关于ω的变化曲线,-βi的极大值和其对应的ω即为翼尖涡在该工况、该截面的空间不稳定性放大率和扰动频率。
对其他截面的流场作相同的处理,可以得到不同流动条件与流向截面的翼尖涡的空间与时间不稳定性、不稳定性放大率以及对应的扰动频率的演化过程。
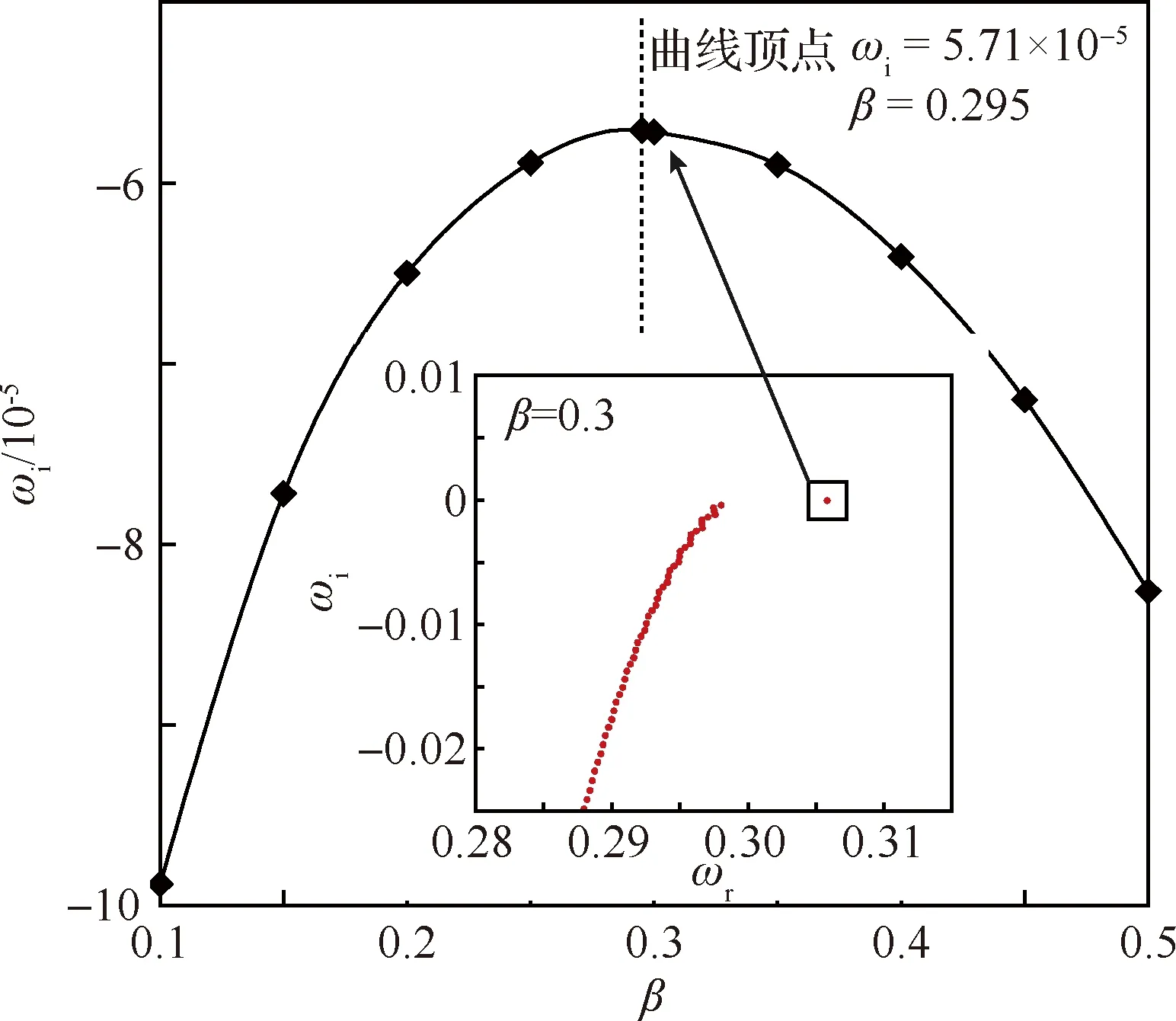
图8 x/c=4.8、α=10°、U∞=25 m/s条件下,时间不稳定性扰动主模态的放大率ωi与其扰动波数β的变化曲线(插图为β=0.3的时间不稳定性特征值谱,小方框中为其扰动主模态的特征值)Fig.8 Variation of growth rate ωi of temporal primary mode with its streamwise wavenumber β at x/c=4.8,α=10°,U∞=25 m/s (the inset being the eigenvalue spectrum of temporal instability at β= 0.3,with eigenvalue in the box corresponding to its primary mode)
4.2 翼尖涡不稳定性特征演化
对各个工况下翼尖涡时间和空间不稳定性放大率进行计算,得到不稳定性放大率关于流向x的变化规律,如图9所示。结果表明,在试验测量的各工况下,翼尖涡在所测量的尾迹区范围内(x/c=0.6~6.0)的时间/空间不稳定性放大率ωi和-βi均小于0,意味着翼尖涡在所测量的条件下均处于临界稳定状态。因此在试验观察中,翼尖涡没有发生失稳和破碎现象。但是,翼尖涡不稳定性放大率沿流向均呈现出放大趋势,随着翼尖涡在远场(10倍展长以外的区域)的衰减,不稳定性将占据主导作用[1],从而导致翼尖涡在远场发生失稳甚至破碎现象。受试验段长度的限制,后续研究中需对更远处的尾迹截面进行测量,以对此予以验证。
进一步分析雷诺数与迎角对翼尖涡空间不稳定性的影响,如图10所示,其中灰色区域示意了各工况下不稳定性放大率在流向x上的变化范围。可发现随着雷诺数的增加,不稳定性放大率逐渐增大,并且在迎角为8°和10°条件下的翼尖涡不稳定性明显大于4°条件下的情况。图9中虽然4°迎角下翼尖涡不稳定增大率随流向增长较快,但几乎始终小于8°与10°迎角下的增长率。
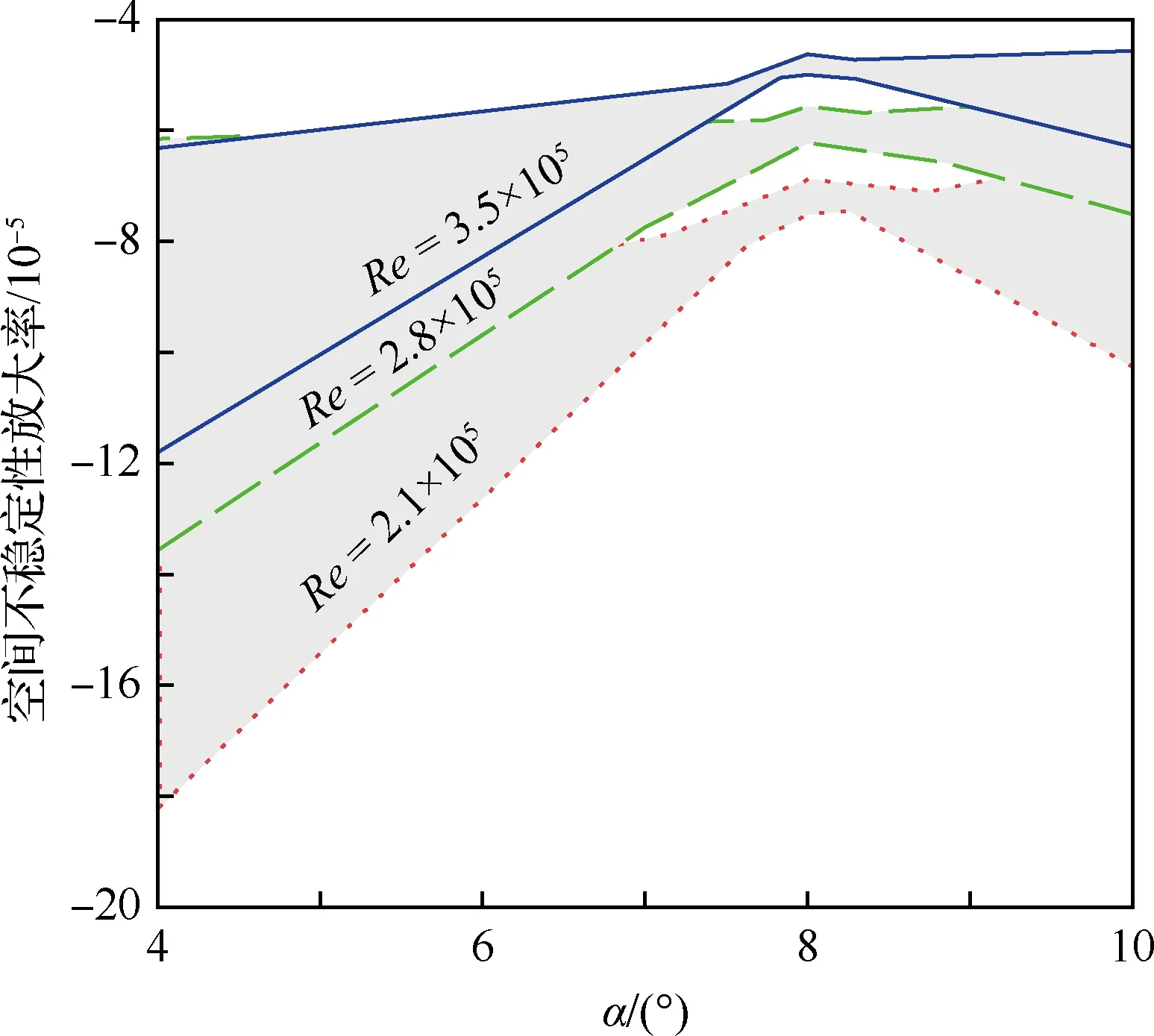
图9 不同雷诺数条件下空间不稳定性放大率与迎角关系Fig.9 Spatial instability amplification ratio via angles of attack at different Reynolds numbers
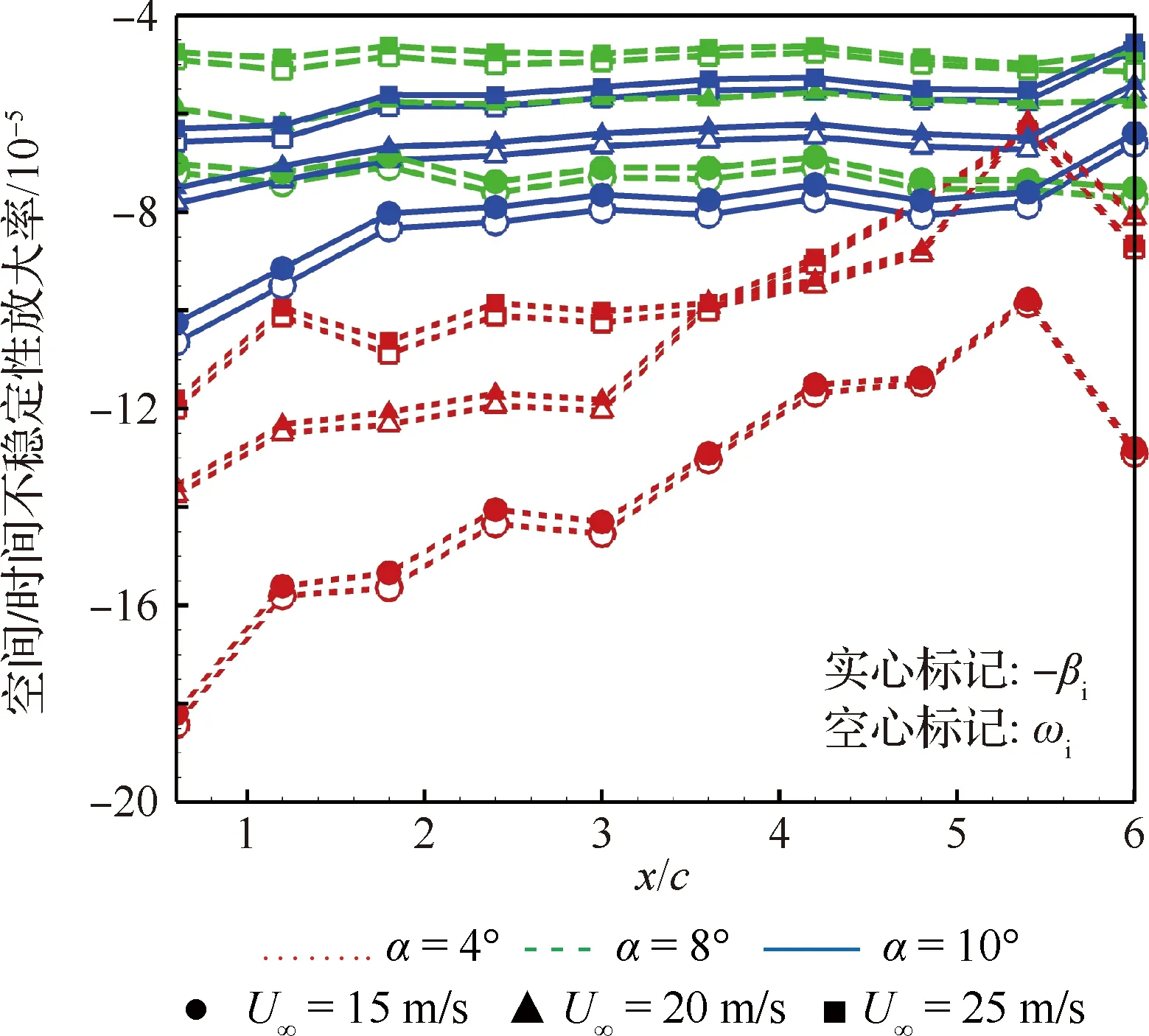
图10 空间/时间不稳定性放大率随流向变化Fig.10 Streamwise evolution of spatial/temporalinstability amplification ratio
以上线性稳定性分析的结果解释了2.1节中图3所显示的大迎角条件下摇摆幅值随流向增长更迅速的现象。由于真实流动中的微小扰动客观存在(其来源可能是风洞壁面或大气环境等),当翼尖涡受到扰动后,在小迎角条件下(4°),因其自身空间不稳定性较弱,扰动不易随流向放大,因此表现为涡摇摆幅值随流向的缓慢增长;而在大迎角条件下(8°,10°),翼尖涡自身空间不稳定性较强,扰动在空间上相对于小迎角条件更容易被放大,因此翼尖涡摇摆的幅度随流向增大趋势更为明显。而由于各流向截面x的ωi<0,由流动上游传输的扰动将随时间t不断衰减,因此试验中各截面的翼尖涡未发生破碎,而是仅表现出包含有主导频率的摇摆运动。
4.3 翼尖涡摇摆波数与频率
通过线性稳定性分析还可以得到翼尖涡不稳定模态在空间与时间上的无量纲波数βr和频率ωr,如图11所示。在沿流向发展过程中,扰动的无量纲扰动波数βr与频率ωr均有所减小,并且相同雷诺数条件下8°与10°迎角的扰动频率基本小于4°迎角;当雷诺数增加时,扰动频率有所增加,薛栋[8]通过水槽试验也得到了相似的规律。
此外,在测量范围内的各尾迹截面下,翼尖涡扰动无量纲波数βr与频率ωr均十分接近。由此可知,在试验测量的流动条件下,翼尖涡扰动的无量纲相位速度接近于1,即扰动的相位速度和自由来流速度U∞基本一致,Edstrand等使用Bi-Global LSA对翼尖涡的稳定性分析也得到了相似的结果[25]。这与平面Poiseuille流中扰动的无量纲相位速度小于2/3的结果截然不同[29],其原因是试验测量的翼尖涡并不包含任何类似Poiseuille流中的边界层结构而限制扰动的传递。与Poiseuille流不同,翼尖涡流向速度基本接近自由来流速度,基于临界层理论[30],其扰动相位速度也因此明显大于Poiseuille流。此外根据Gaster变换-ωi/βi=∂ωr/∂βr=vg[31],还可以得到扰动的群速度vg,即扰动波包的传输速度。由图9中翼尖涡在各尾迹截面的时间与空间不稳定性放大率较为接近的结果,可以得出扰动群速度vg≈1,这也与图11所示ωr和βr的结果一致。扰动群速度近似为1的结果意味着扰动的波包将向下游传输,因而试验中翼尖涡的不稳定性特征是对流的而非绝对的[30,32]:随着扰动向下游的发展,翼尖涡会在远场的某一截面位置发生失稳;但扰动不会同时向上游传输而使翼尖涡随时间发生全局的破碎,这与试验中x/c=0.6~6.0的范围内翼尖涡在200 s的观测时间内均未发生破碎的现象相符合。
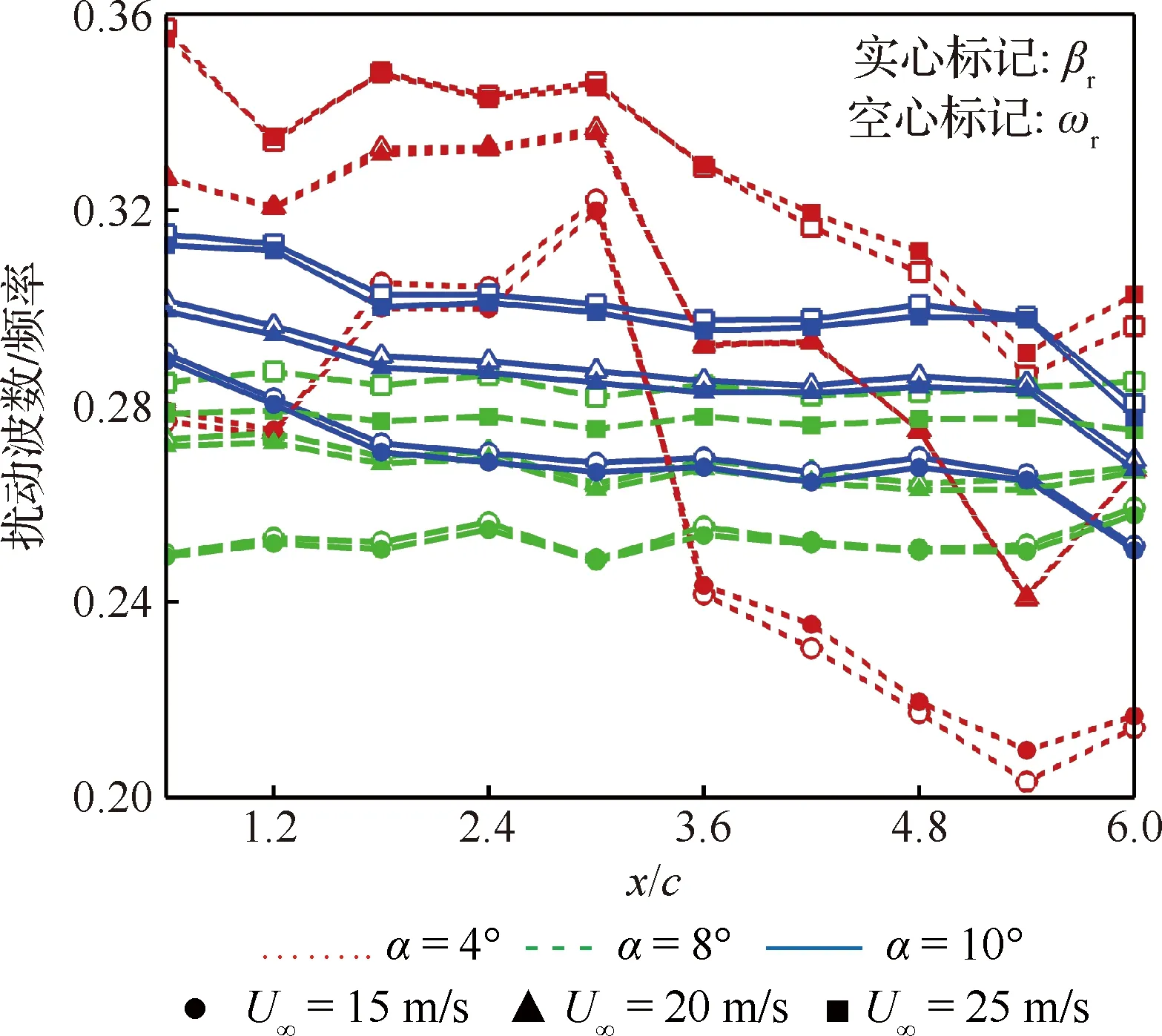
图11 不同工况下扰动波数与频率随流向变化Fig.11 Streamwise variation of perturbation wavenumber and frequency at different conditions
进一步由无量纲频率ωr可得,各试验工况下翼尖涡扰动的斯特劳哈尔数Sr均在0.045附近,根据无量纲参数c=0.203和来流速度U∞,可得到翼尖涡在U∞=15,20,25 m/s下的扰动频率f分别为3.3、4.4、5.5 Hz,这与Devenport[5]和Bailey[9]等试验测得的翼尖涡摇摆主导频率可比。受限于试验激光脉冲频率为1 Hz,对于采集得到的翼尖涡涡核位置时间序列无法通过傅里叶变换得到其主频率,因此后续需要提高试验激光脉冲频率以对计算得到的频率进行验证。
4.4 翼尖涡摇摆机制
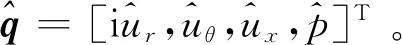
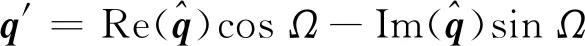
(7)
式中:Ω=βx+nθ-ωt,转换到笛卡儿坐标系后可以得到速度扰动在x、y、z方向的分量u′、v′、w′的分布。
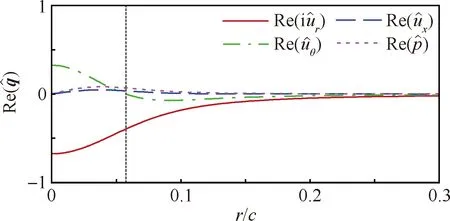

图12 α=10°,U∞=20 m/s,x/c=6.0时翼尖涡空间的不稳定性扰动解(虚竖线为最大切向速度位置)Fig.12 Disturbance of spatial instability of wingtip vortex at α=10°,U∞=20 m/s,x/c=6.0(dashed vertical line indicating location of maximum tangential velocity)
进一步计算翼尖涡最不稳定模态的横向合速度u′tr=[v′,w′]T,并考虑扰动随时间t的相位变化。图14显示了在相位t= 0,T/4,T/2,3T/4下的u′tr分布与试验测量的翼尖涡瞬时涡核分布的比较情况,其中T为扰动的时间周期,根据4.3节中计算的扰动频率,在α=10°,U∞=20 m/s,x/c=6.0条件下,T=0.24 s。从图14(b)和图14(c)可以观察到,横向扰动速度u′tr在其各个相位都具有明显的方向性,并且集中于涡核位置,图中箭头示意了u′tr在涡核附近速度矢量的连线;由u′tr在各相位的分布可以发现,横向扰动速度u′tr随时间t呈现周期性的旋转。不稳定性特征引起的横向速度扰动u′tr的方向性以及周期性旋转共同导致了翼尖涡的摇摆运动,表现为图14(a)中试验测量的涡核在两个方向上均存在摇摆运动分量,并且摇摆运动含有主导频率,是翼尖涡产生摇摆运动的内在原因。图14(a)中箭头示意了摇摆运动的主轴,其长度表征了摇摆幅值,虽然由LSA得到的扰动模态随时间t仅仅表现为周期性旋转,但由两个主轴方向的摇摆幅值可得,该条件下的翼尖涡摇摆运动仍具有各向异性特征,其原因可能有以下几种。首先,作为扰动的外在来源之一,自由来流中的湍流在各方向非均匀[9],使特定相位的不稳定模态速度扰动受到放大或抑制,引起摇摆运动在不同方向的幅值产生偏差;其次,涡核区域的湍流小涡结构受到翼尖涡自身的拉伸作用会产生各向异性的雷诺正应力[33-34],进一步诱导翼尖涡摇摆发生各向异性。然而,作为翼尖涡摇摆的内在原因,横向扰动速度在各相位所具有的方向性特征仍是摇摆运动发生各向异性的前提,其具体成因则还有待更进一步的分析与研究。
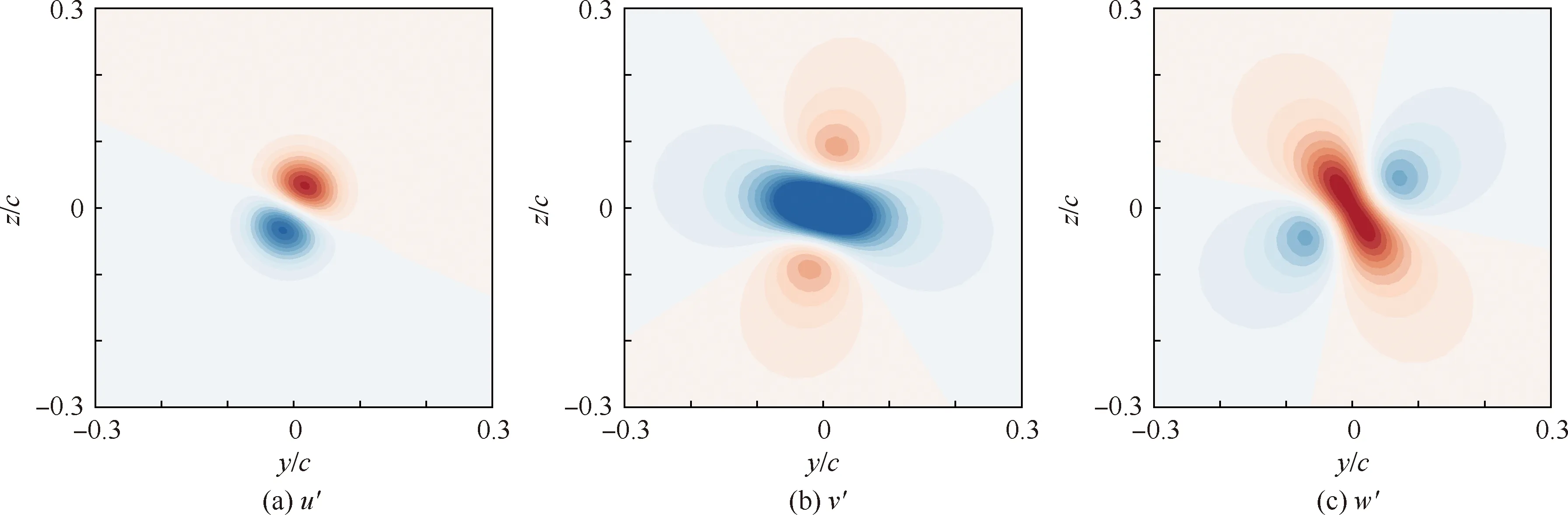
图13 α=10°,U∞=20 m/s,x/c=6.0时翼尖涡最不稳定模态的u′、v′、w′云图(v′、w′的云图范围为[-0.3,0.3],u′的云图范围为[-0.1,0.1])Fig.13 Contours of u′,v′,w′ of the most unstable mode of wingtip vortex at α=10°,U∞=20 m/s,x/c=6.0 (range of v′,w′ :[-0.3,0.3],and range of u′:[-0.1,0.1])
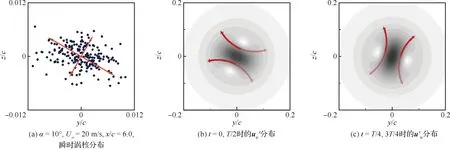
图14 试验测量的瞬时涡核分布与LSA计算的扰动模态比较Fig.14 Comparison between experimental instantaneous vortex core distribution and disturbance mode by LSA
由此,根据翼尖涡最不稳定扰动模态及其相位变化与试验测量得到的翼尖涡摇摆运动方向的匹配关系,可以进一步证明翼尖涡的稳定性特征是其摇摆运动的内在原因,其扰动模态决定了所呈现出的摇摆运动特征:涡核区域的横向扰动速度u′tr具有明显的方向性,诱导翼尖涡发生摇摆运动;u′tr的方向随相位的周期性变化则使翼尖涡摇摆有别于一维的随机振荡,而是表现为在各方向均含有分量且具有主频的摇摆运动。
5 结 论
通过SPIV试验观察翼尖涡的摇摆现象,得到了其摇摆幅值随流向放大并且具有各向异性的特征,进而使用线性稳定性分析对摇摆运动修正后的翼尖涡进行研究,定量得到其稳定性、摇摆频率和时间/空间的不稳定性放大率随流向变化,以及这些特征与雷诺数和迎角的关系,揭示了翼尖涡不稳定性的演化规律,并阐释翼尖涡摇摆机理以及稳定性对翼尖涡流动的影响机制。
1)各工况下翼尖涡摇摆幅值均沿流向放大,且摇摆运动在大迎角条件下在远场具有明显的各向异性,由近场的各向同性特征随流向逐渐发展为机翼法向的摇摆幅值明显大于展向摇摆幅值的各向异性特征。
2)翼尖涡受到扰动后,其不稳定性模态决定所表现出的摇摆运动特征,而其不稳定性决定扰动随时间/空间的放大速率。翼尖涡在4°迎角下的不稳定性放大率明显小于8°和10°迎角,即翼尖涡在大迎角条件下更不稳定,这是导致大迎角时摇摆幅值随流向迅速增长的原因。
3)各试验工况下翼尖涡扰动的斯特劳哈尔数在0.045附近,扰动频率约为3~5 Hz。由时间与空间不稳定性分析结果得出扰动的群速度约为1,扰动将向下游发展,因此试验中的翼尖涡表现出对流不稳定性特征。
4)由线性稳定性分析得到的翼尖涡不稳定模态,发现翼尖涡的速度扰动局限在涡核区域内,其在涡核处的横向速度扰动具有明确的方向性,并且随相位变化作周期性旋转,这是导致翼尖涡发生摇摆运动的原因所在。
致 谢
感谢王笑、秦苏洋、王煜凯和李林颖在试验和论文撰写过程中提供的帮助与宝贵意见。

