基于PTE的多雷达航迹融合算法

张天宇，郑坚，田卓尔，荣英佼，郭云飞，申屠晗

1.杭州电子科技大学 自动化学院，杭州 310018 2.中国电子科技集团公司 第二十八研究所，南京 210014 3.四川大学 电子信息学院，成都 610064 4.近地面探测技术重点实验室，无锡 214035

雷达通过自身发射的电磁波，对位于监视区域内的目标进行探测，并利用回波反射的特征对目标进行定位与跟踪[1]，受到了国内外学者的广泛关注。其中被动多基站雷达(Passive Multistatic Radar,PMR)体积小，抗干扰能力强，自身静默，具有较强的隐身/反隐身能力。除此之外，PMR利用双、多基站的空间多样性、频率多样性大幅提高了系统对低空和隐身目标的跟踪性能，成为了一个重要的研究分支[2-7]。

由于多基站雷达具有扩展空间覆盖范围，提高可信度，增强可靠性，改善跟踪精度的优势[8-9]，所以研究多雷达航迹融合技术显得尤为重要。文献[10]研究了集中式和分布式融合算法。在分布式融合框架下，文献[11]提出了Bar-Shalom-Campo规则融合算法。文献[12]提出了基于转换坐标卡尔曼滤波器的多传感器目标跟踪融合算法。由于各传感器估计误差之间的互协方差矩阵难以计算，文献[13]利用Fisher信息矩阵融合算法处理互协方差矩阵未知情况下的航迹融合问题。而文献[14]针对互协方差矩阵未知的情况，提出了基于集合论的松弛切比雪夫中心协方差交互融合算法与基于信息理论的快速协方差交互融合算法。根据融合结构的不同，文献[15-16]比较了不带记忆的协方差交互融合算法与带记忆的协方差交互融合算法的优劣。目前大多数多传感器航迹融合方法未考虑虚假航迹的融合问题。针对虚假航迹问题，文献[17]提出基于目标存在性的序贯航迹融合算法，但仅用于处理一个本地的传感器和一个遥远的传感器的融合。在文献[17]的基础上，文献[18]利用航迹信息的反馈提出了带记忆的多传感器航迹融合方法。但上述两篇文献均没有考虑局部估计误差互协方差矩阵。

为了解决存在虚假航迹时局部估计误差互协方差矩阵未知的被动多基站雷达航迹融合问题，本文提出不带记忆的综合广义凸组合(Integrated Generalized Convex Combination without Memory,IGCCWOM)航迹融合算法，进而考虑前一帧的融合状态，提出了带记忆的综合广义凸组合(Integrated Generalized Convex Combination with Memory,IGCCWM)航迹融合算法。该算法通过综合概率数据关联进行目标状态与协方差矩阵的预测更新，得到目标存在概率(Probability of Target Existence,PTE)以及单接收站的估计航迹集。最后结合目标存在概率，推导出不带记忆的综合广义凸组合算法和带记忆的综合广义凸组合算法，将两个接收站分别估计得到的局部航迹进行航迹关联概率和权值更新，并通过融合PTE得到最终的全局航迹。

1 问题描述

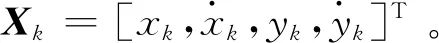
Xk=FkXk-1+vk

(1)

式中：Fk为目标的状态转移矩阵；vk为服从均值为0，协方差矩阵为Qk的高斯过程白噪声。

在杂波环境下假设PMR系统第s个接收站第k帧的量测集合为[6]

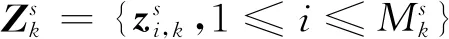
(2)

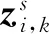
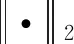
(3)

(4)

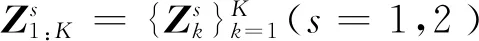
2 航迹融合算法

本节基于文献[17-18]提出的不带记忆的航迹融合(Track-to-track Fusion without Memory,TFWOM)和带记忆的航迹融合(Track-to-track Fusion with Memory,TFWM)算法构建IGCCWOM和IGCCWM航迹融合算法。

其中TFWOM和TFWM算法框架如图1所示。TFWOM算法包括3个基本步骤：① 基于两个接收站K帧的量测集合分别通过综合概率数据关联(Integrated Probabilistic Data Association,IPDA)算法得到两个接收站的目标估计航迹集和对应的PTE。② 将两个接收站的局部航迹估计和PTE进行航迹关联概率计算和卡尔曼滤波增益更新，然后融合两个接收站的航迹估计得到全局目标航迹估计以及融合PTE。③ 最后基于融合PTE的阈值判断，去除虚假航迹，得到真实目标航迹。TFWM算法基本流程与TFWOM一致，不同之处在于对于TFWM算法，步骤②中将前一帧融合状态进行反馈。

但TFWOM和TFWM算法都忽略了局部估计误差互协方差矩阵，导致融合精度有一定的损失，所以本文在考虑局部估计误差互协方差矩阵的情况下，同时利用PTE信息，提出了IGCCWOM和IGCCWM航迹融合算法。其框架如图2 所示。IGCCWOM航迹融合算法基本流程与TFWOM一致，不同之处在于对于IGCCWOM航迹融合算法，步骤②中除了将两个接收站的局部航迹估计和PTE进行航迹关联概率计算，还进行了权值更新，从而将局部估计误差互协方差矩阵以权值的形式表现出来。而IGCCWM航迹融合算法步骤②中在IGCCWOM航迹融合算法的基础上将前一帧融合状态进行反馈。以下分IPDA模块和航迹融合模块具体论述上述算法的构建过程。

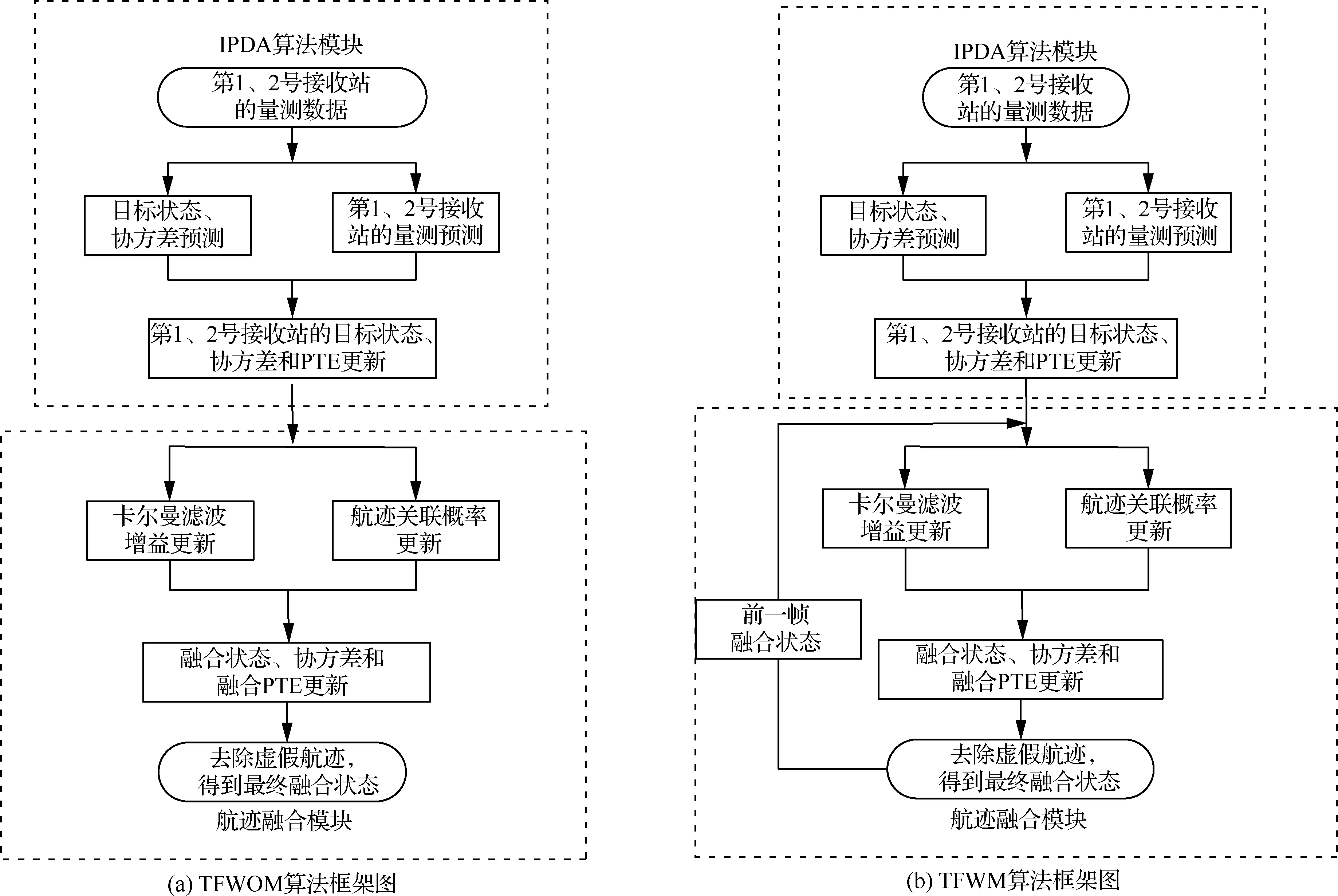
图1 TFWOM和TFWM算法框架图Fig.1 Block diagram of TFWOM and TFWM algorithms

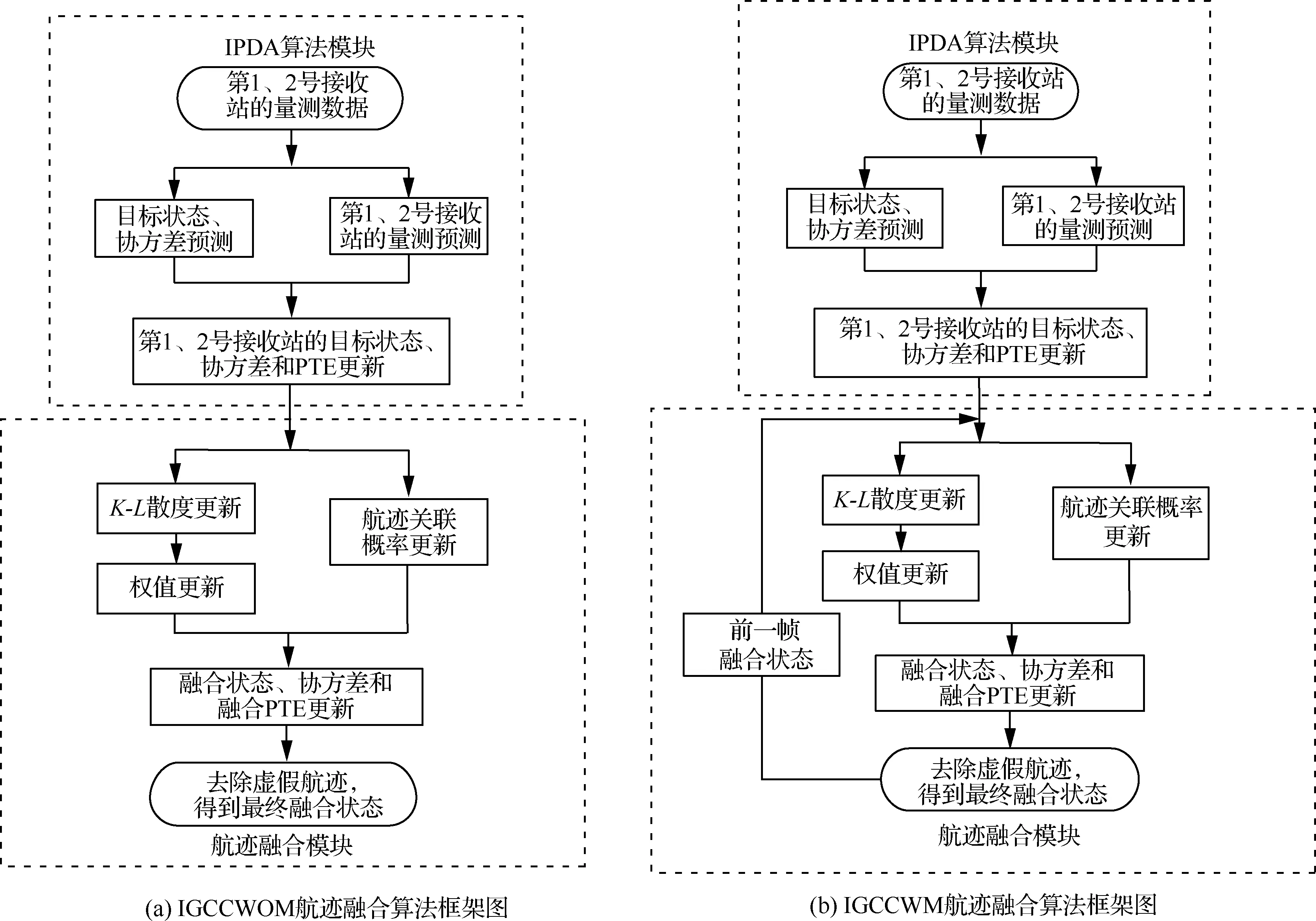
图2 IGCCWOM和IGCCWM航迹融合算法框架图Fig.2 Block diagram of IGCCWOM and IGCCWM track-to-track fusion algorithms

2.1 综合概率数据关联模块

本节通过IPDA算法对量测数据进行处理，得到单接收站的航迹。简便计，在不引起混淆的情况下，接收站上标s在本节中省略。

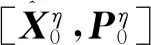
步骤2状态预测。

(5)

状态协方差矩阵预测

(6)

量测预测为

(7)

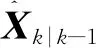
步骤4目标存在概率更新。

假设k-1帧的目标存在性Uk-1已知：

(8)

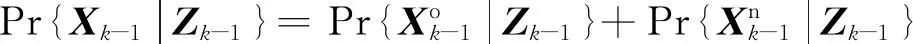
(9)

由全概率公式可得目标存在性预测

Uk|k-1=ΩTUk-1

(10)

式中：Ω为目标存在性转移概率矩阵。

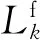
(11)

式中：PD表示检测概率；PG表示门概率。根据贝叶斯理论，目标存在概率PTE更新如下[20]

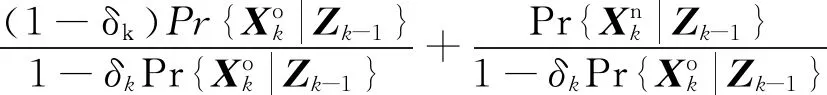
(12)

式中：

(13)

步骤5目标状态与误差协方差矩阵更新。

第k帧跟踪门内第i个量测zi,k源自目标的后验概率为[20]

(14)

目标没有产生量测的后验概率为

(15)

则目标状态更新方程为

(16)

协方差矩阵更新方程为

(17)

2.2 航迹融合模块

本节针对局部估计误差之间的互协方差矩阵未知的问题，通过基于PTE的航迹融合方法对2.1节得到的两个接收站的航迹估计和PTE进行航迹关联概率计算和权值更新，然后融合两个接收站的航迹估计得到全局目标航迹估计以及融合PTE，并基于融合PTE的阈值判断，去除虚假航迹，得到真实目标航迹。

2.2.1 不带记忆的综合广义凸组合融合算法

(18)

(19)

(20)

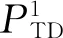
(21)

(22)

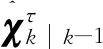
(23)

从而融合PTE可以通过式(24)更新为

(24)

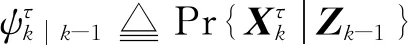
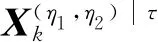
(25)

(26)

(27)

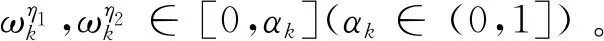
在信息理论中，Shannon信息熵描述不确定度。相对熵或K-L距离(Kullback-Leibler Divergence)是两种分布之间的密切关系的一种度量[14]。因为这里是两个接收站的估计进行融合，所以整体自适应参数αk能通过式(28)得到[14]：

αk=αη1η2,k

(28)

定义为

(29)

式中：

(30)

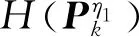
(31)

其中：D(P1,P2)为两个误差协方差矩阵P1、P2之间的K-L散度

(32)

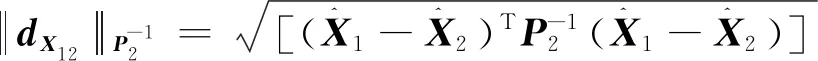
(33)

IGCCWOM航迹融合算法的权值计算为[14]

(34)

(35)

(36)

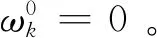
综上即可得到融合航迹状态估计及误差协方差矩阵式(18)和式(19)。

2.2.2 带记忆的综合广义凸组合融合算法

IGCCWM航迹融合算法在IGCCWOM航迹融合算法的基础上，将前一帧融合状态进行反馈。与IGCCWOM航迹融合算法相比，存在以下区别。

IGCCWM航迹融合算法的融合状态估计与误差协方差矩阵更新方程用式(37)～式(39)替代式(25)～式(27)：

(37)

(38)

(39)

整体自适应参数αk的计算由式(40)代替式(28)：

αk=(αη1η2,k+αη1τ,k+αη2τ,k)/3

(40)

式中：αη1η2,k、αη1τ,k、αη2τ,k的定义类似式(29)。

权值计算用式(41)～式(43)替代IGCCWOM航迹融合算法中的式(34)～式(36)：

(41)

(42)

(43)

式中：

(44)

(45)

(46)

(47)

其中K-L散度D(P1,P2)的定义见式(32)。

考虑航迹关联概率，最终得到融合航迹状态估计为

(48)

融合误差协方差矩阵为

(49)

3 仿 真

仿真利用两个接收站一个外辐射源的PMR系统对一个近似匀速直线运动的目标进行跟踪。其中两个接收站已经进行了空间配准，都在系统坐标系下生成量测。具体场景参数标记如下：

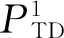
表1 目标、接收站和外辐射源初始状态Table 1 Initial state of target,receiver,and transmitter

图3给出了接收站1接收到的航迹，即经过IPDA算法得到的航迹，包括目标真实航迹和虚假航迹。其中航迹1为真实航迹，航迹2和航迹3为虚假航迹。图4给出了接收站2接收到的航迹。其中航迹1为真实航迹，航迹2和航迹3为虚假航迹。

由图3和图4可知，单接收站得到的航迹存在虚假航迹。

在杂波环境下，经过本文所提的IGCCWOM和IGCCWM航迹融合算法进行航迹融合后，通过对融合航迹目标存在概率的判断，去除虚假航迹，得到真实航迹，如图5所示。

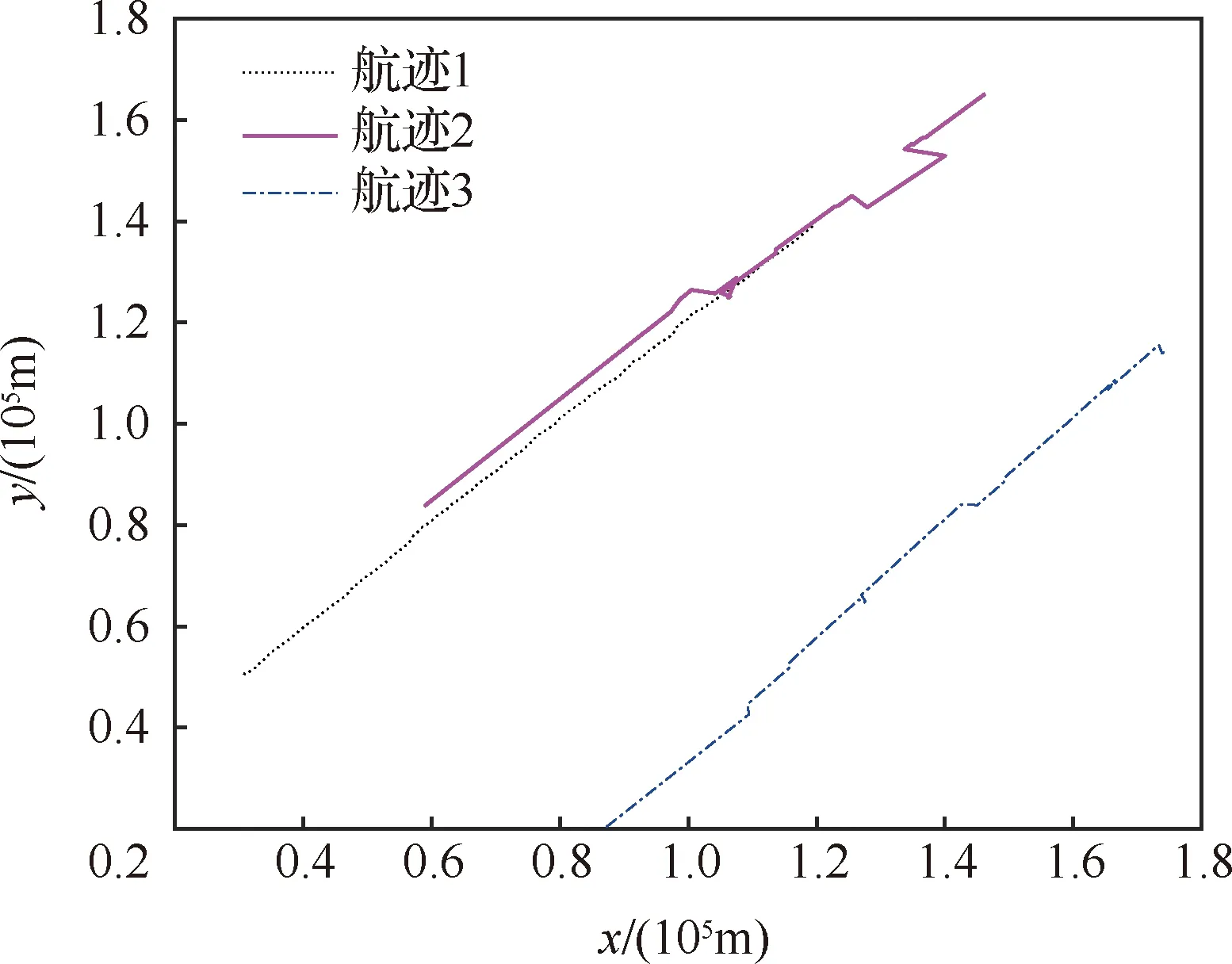
图3 接收站1的航迹Fig.3 Track of receiver one

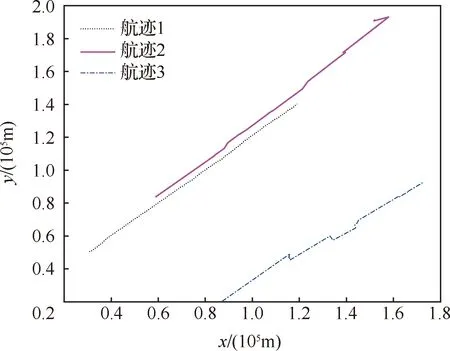
图4 接收站2的航迹Fig.4 Track of receiver two

图5 IGCCWOM与IGCCWM航迹Fig.5 Track of IGCCWOM and IGCCWM

由图5可知，通过对融合航迹目标存在概率的判断，能够有效去除虚假航迹，且IGCCWOM、IGCCWM航迹融合算法可以跟踪上目标航迹。

图6描述了在PMR系统中，不同融合算法进行航迹融合时对目标跟踪的影响。其中对比算法有基于信息理论准则的无记忆的快速容错广义凸组合(Fast Fault-tolerant Generalized Convex Combination based on Information-Theoretic Criterion without Memory,IT-FFGCCWOM)航迹融合算法与基于信息理论准则的带记忆的快速容错广义凸组合(Fast Fault-Tolerant Generalized Convex Combination based on Information-Theoretic Criterion with Memory,IT-FFGCCWM)航迹融合算法[14]，不带记忆的航迹融合(Track-to-track Fusion without Memory,TFWOM)和带记忆的航迹融合(Track-to-track Fusion with Memory,TFWM)算法[21]。各个算法目标位置的RMSE如图6所示。

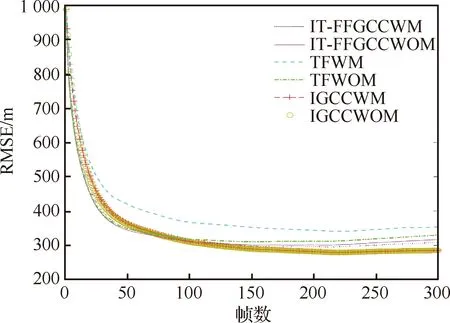
图6 目标位置的RMSEFig.6 RMSE curves of target position

从图6可以看出，IGCCWOM、IGCCWM航迹融合算法的目标位置估计均方根误差(Root Mean Sguared Error,RMSE)较TFWOM、TFWM算法和IT-FFGCCWM、IT-FFGCCWOM航迹融合算法低。由于IT-FFGCCWM、IT-FFGCCWOM航迹融合算法未考虑目标存在性，而TFWOM、TFWM算法未考虑局部估计误差互协方差矩阵，所以对目标状态融合效果比IGCCWOM、IGCCWM航迹融合算法差。

表2统计了100次蒙特卡罗下不同检测概率各种算法稳定时的目标状态估计RMSE，正确航迹率和100次蒙特卡罗运行时间。由表2可知，在PMR的杂波环境下，无论在高检测概率还是在较低检测概率情况下，与单接收站相比，融合算法有更高的正确航迹率，且位置估计RMSE更低。这是由于各个融合算法利用了两个接收站的信息，扩大了探测范围，可以从两个不同的角度观测到目标信息，从而改善了目标航迹质量。而IGCCWOM和IGCCWM航迹融合算法的正确航迹率比TFWOM和TFWM算法更高，位置估计RMSE比TFWOM、TFWM算法更低。这是由于IGCCWM算法和IGCCWM算法考虑了局部估计误差互协方差矩阵，而TFWOM和TFWM算法忽略了局部估计误差互协方差矩阵的计算，同时这也导致了IGCCWOM和IGCCWM算法的运行时间比TFWOM和TFWM算法更长。由于IT-FFGCCWM和IT-FFGCCWOM航迹融合算法没有目标存在概率的计算，所以运行时间也比所提算法短。

本文所提算法除了适用于上述仿真环境，同时也适用于目标做加速运动或曲线运动模型；而且也适用于多个接收站和一个外辐射源的PMR模型。

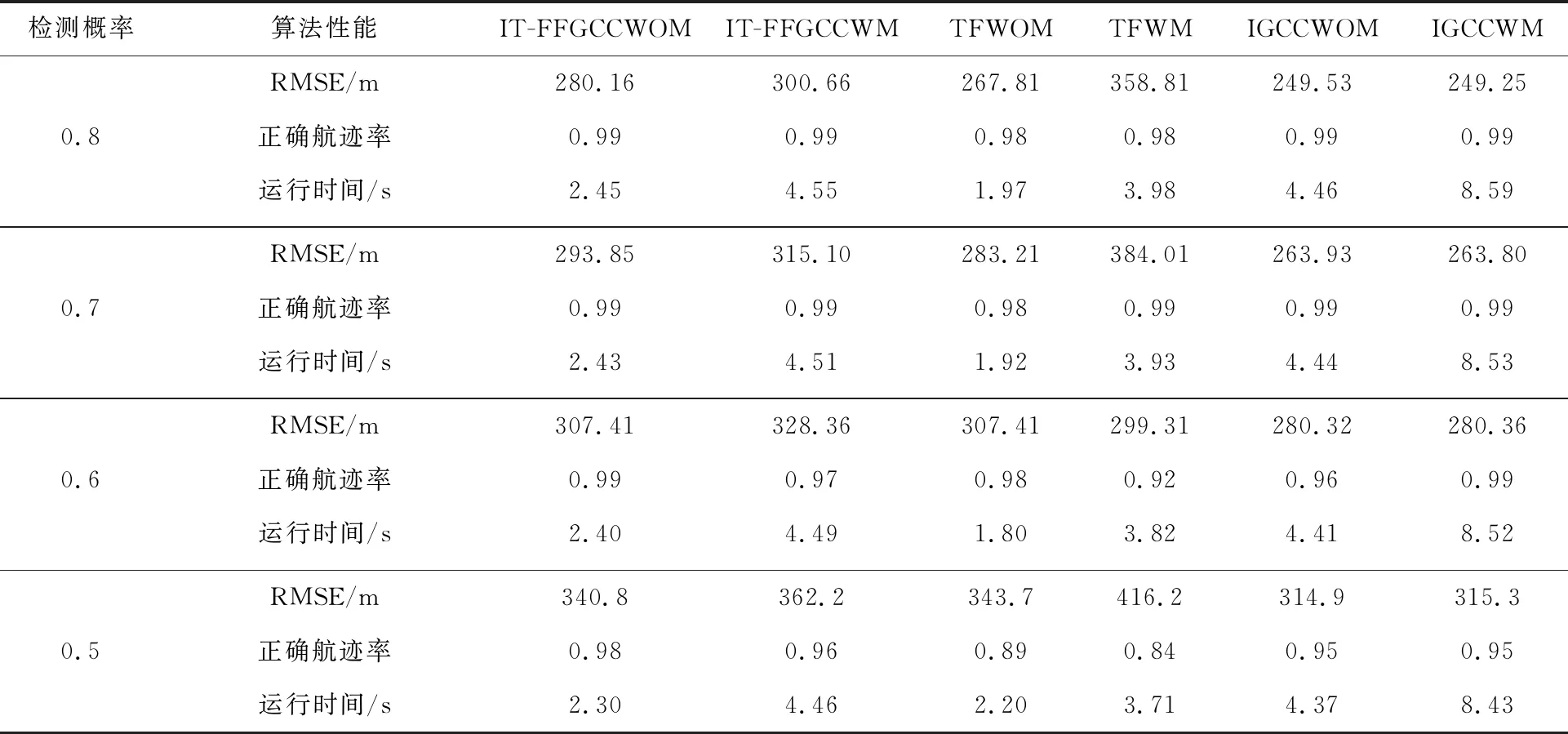
表2 不同检测概率下各个算法的航迹性能比较Table 2 Comparison of track performance of each algorithm under different detection probabilities

4 结 论

1)本文针对杂波背景下的被动多基站雷达航迹融合问题，提出基于目标存在概率的航迹融合算法。

2)所提算法将目标存在概率信息引入被动多基站雷达航迹融合中，推导了IGCCWOM和IGCCWM航迹融合算法，解决了局部估计误差互协方差矩阵未知条件下的航迹融合问题。

3)仿真结果表明了所提算法与对比算法相比，有更高的正确航迹率，对目标位置估计更准确。