翼上螺旋桨构型耦合气动特性及翼型优化设计
范中允,周洲,*,祝小平,郭佳豪
1.西北工业大学 航空学院,西安 710072 2.西北工业大学 无人机特种技术重点实验室,西安 710065
目前,对新概念高效垂直/短距起降飞行器的研究中普遍考虑了动力与机翼/机身的耦合设计,以实现高效气动增升,例如将螺旋桨布置于机翼上方,形成“翼上螺旋桨”(OTWP)构型。这一构型最初来源于“半环形机翼”(Channel Wing,CW,也叫半涵道机翼),是一种特殊外形的OTWP构型,1942年由Custer首次提出这一飞机设计概念,该构型在低速、垂直/短距起降状态中有较好的优势[1]。20世纪80年代Johnson与White[2-3]设计了正常式、鸭式、前掠翼等不同布局的OTWP构型飞机,并进行了风洞试验。2000年,Gunther等[4]通过试验研究了Blick理论对半环形翼性能估算的准确性。2002年,Englar和Campbell[5-6]结合上表面吹气增升技术,对Custer的半环形翼飞机进行了进一步风洞试验,表明吹气增升技术和OTWP构型均可以显著提高低速状态下机翼的升力系数和失速迎角,失速迎角可从15°提高到约45°。2014年,Müller等[7]采用CFD方法研究了带有吹气襟翼的干净机翼、拉进式螺旋桨构型、平直翼OTWP构型、半环形OTWP构型的气动特性。为提高对半环形机翼的计算准确性,Müller等[8]在激励盘模型中加入了叶素理论修正。2016年,Beck等[9]研究了半环形机翼的气动噪声问题。王红波等[10-11]针对包括OTWP构型在内的多种螺旋桨布局方式及参数进行了系统研究,发现螺旋桨位于80%弦长、襟翼偏角75°时,耦合诱导增升效果最好。2018年,Marcus等[12]通过试验和计算研究了带襟翼的OTWP构型中翼面压力及桨盘压力分布的变化趋势,并研究了风车状态下螺旋桨与翼面的耦合效应。
与此类似的还有“上表面吹气增升” (Upper Surface Blowing)技术[13-18],该构型主要应用喷气发动机作为动力,利用Coanda效应[13],设计翼上表面引导发动机喷流向下偏转,可产生较好的增升效果。
OTWP构型下,由于翼剖面中有能量输入,与通常巡航条件下的翼型流场结构有较大不同,桨盘后滑流的诱导增升效果与翼面的弯度和弯折曲率有密切的关系[13],较好的增升效果需要适中的弯度和曲率,以确保流动尽可能附着,充分利用Coanda效应,因此OTWP构型的翼剖面也需要针对性设计。目前,大多数关于OTWP的文献主要是进行流场分析、位置参数影响、布局形式对比研究等,处于布局性能的摸索阶段,对该构型机翼的翼型设计方法尚为空白,机翼设计的研究也较为少见。
在OTWP构型复杂非定常流场的研究方法上,绝大部分学者采用试验方法或CFD方法,也有部分学者建立了面元法/叶素理论耦合方法[12]、势流理论等快速计算方法,但目前快速算法难以准确计算复杂分离流动。由于部分OTWP构型存在前缘分离-再附着现象或后缘分离现象[4],尤其在考虑翼型变形的设计和优化问题时部分构型可能产生流动分离,因此快速算法难以对此进行可靠计算,仅能对拉进式螺旋桨构型或弯度较小、流动附着的部分构型进行分析。全尺寸CFD模型在设计计算上会占用过多资源,为了节省计算资源,动量源法[19-25]逐渐在国内外发展起来。该方法用薄盘代替螺旋桨,在薄盘内采用叶素理论对桨叶载荷进行计算,并转换成动量源项,加入Navier-Stokes方程进行求解,以此对桨盘进行模拟。此方法可以显著减少计算网格量,并可以得到较为准确的速度和压力分布。
针对上述问题,本文以半环形翼上螺旋桨(CW)布局为研究对象,首先对螺旋桨-气动面耦合流场特征进行计算分析,采用检验动量源法及多重参考系(Multiple Reference Frame,MRF)、滑移网格方法对该构型进行可靠性计算;然后,建立了OTWP构型参数化模型和变形程序,搭建了翼上螺旋构型翼剖面形状的优化框架,开展了诱导增升翼型设计研究,进一步分析优化前后的翼型参数变化及增升机理;最后对优化前后的CW构型三维机翼进行CFD计算分析,验证本文优化框架的可行性。
1 数值模拟方法
1.1 涵道螺旋桨计算与试验验证
为证明本文CFD计算方法的可行性,选取1962年NASA某涵道螺旋桨试验[26]数据进行MRF、滑移网格非定常(UNST)、动量源方法(Momentum Source Method,MSM)的算例验证,模型如图1所示,参数详见文献[26]。
试验转速为8 000 r/min,为与本文计算状态类比,选择小来流状态,桨盘载荷约为1 580 N/m2,前进比为0.032,来流速度为1.626 m/s,选择试验迎角90°。MRF及UNST方法,静止域结构化网格为64.98万,为进行网格无关性验证,选用两套旋转域非结构网格,第1套为255.14万(标记为MRF-1),第2套为97.25万(标记为MRF-2)。UNST方法时间步长按照每步旋转2°设置。MSM方法结构化网格为221.2万。CFD求解器采用商用软件Fluent,计算采用剪切应力输运(SST)k-ω湍流模型(下文保持湍流模型不变)。计算结果与试验数据对比如表1所示,其中CT为桨叶拉力系数,Tp/T0为桨盘拉力与总拉力的比值,CQ为桨叶扭矩系数。

图1 NASA涵道螺旋桨模型Fig.1 NASA ducted propeller model

表1 试验与计算结果对比Table 1 Comparison of test and computation results
由MRF-1与MRF-2对比反映出网格量变化对计算结果影响微弱,可忽略不计;真实桨叶模型方法(MRF、UNST)与试验相比误差较为相近,皆在7%~9%,满足工程应用的要求。由于真实桨叶模型方法的计算误差较为稳定,后文三维计算均给出真实模型计算结果作为参考。受简化假设限制,动量源法误差较其他方法偏大,但考虑到其计算效率较高,下文将研究动量源法对流场变化规律的把握能力,若规律与真实模型一致,则可用于设计优化。
1.2 半涵道模型
由于CW构型与涵道/半涵道的螺旋桨-气动面耦合机理有相似之处,本文分别建立单独螺旋桨、涵道螺旋桨、半涵道螺旋桨3种模型(模型示意图如图2所示),采用MSM、MRF、UNST方法进行计算。图中4叶螺旋桨直径Dprop=0.3 m,桨毂直径Dhub=0.06 m,转速n=11 500 r/min,桨盘载荷DL≈1 500~1 800 N/m2(螺旋桨拉力与耦合特性有关)。涵道/半涵道长度lduct=0.4 m,桨尖与壁面间隙δ=1.5 mm,涵道翼型为Clark Y(桨盘旋转区域经过修形)。静止域网格量约为201.02万~215.04万(视模型有所不同),旋转域网格量约为110.85万,网格如图3所示。本文研究主要针对垂直/短距起降状态,计算状态选取为(下文来流状态相同):来流速度V0=1 m/s(计算收敛预设速度),高度H=0 m。

图2 3种模型示意图Fig.2 Schematic of three models
本节动量源法采用耦合叶素理论的计算方法[25],该方法能够考虑翼面和桨叶之间的干扰,可以得到非均匀桨盘载荷分布,适用于耦合构型的模拟。计算结果如表2所示。表中法向力指涵道壁产生的垂直于桨盘转轴的力。对比发现,涵道螺旋桨比单独螺旋桨的桨盘拉力显著下降,而半涵道螺旋桨的桨盘拉力又回到了较高水平。涵道使得桨盘扭矩降低,而半涵道使得桨盘扭矩增加,同时唇口拉力比涵道大幅下降。桨盘与唇口吸力的合力使得涵道、半涵道的总力效要高于单独螺旋桨,因而体现了螺旋桨与气动面耦合的基本优势。
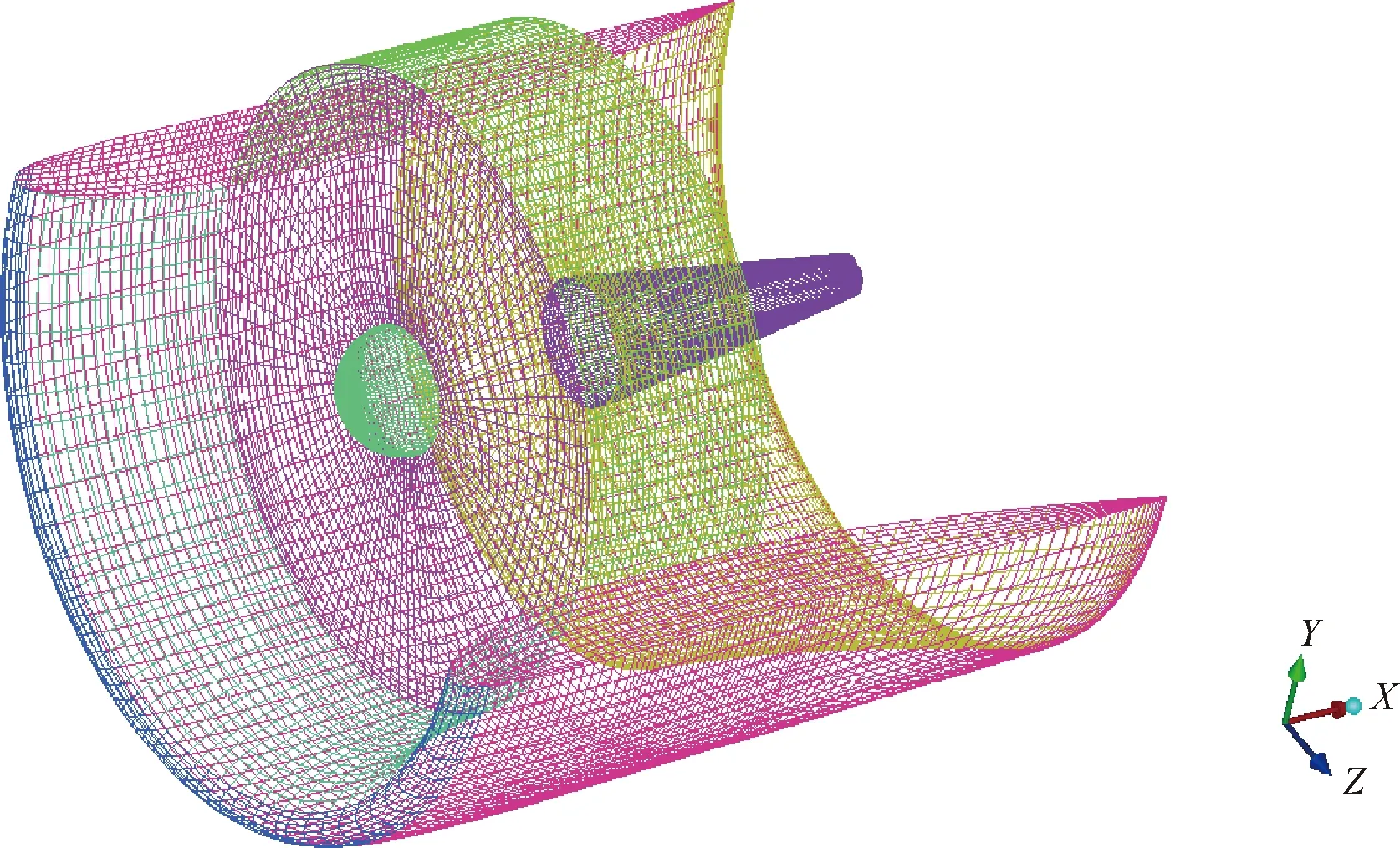
图3 静止域网格(半涵道)Fig.3 Mesh of static zone (semi-duct)

表2 CFD模型计算结果Table 2 Calculation results of CFD model
对单独螺旋桨与涵道螺旋桨的计算,MRF与滑移网格方法较为吻合;动量源方法所得拉力和扭矩较MRF和滑移网格方法显著偏低,这是由于在本文计算状态下,螺旋桨桨根附近叶素处于大迎角状态,而动量源耦合的叶素气动数据来源于翼型面元法计算软件XFOIL,过失速数据是根据升力系数曲线末端非线性外推得到的。外推曲线假设为正弦曲线:
(1)
式中:CLmax为最大升力系数;α为迎角;αmax为最大升力系数对应的迎角。
螺旋桨桨盘0.267R处(R为桨盘半径)的叶素流场如图4所示,叶素处于几乎30°的大迎角状态并已经发生失速。按照前述升力系数外推方法,迎角30°时升力系数约为1.3,但不论是二维翼型还是三维螺旋桨叶素,在该状态下的升力系数均高于1.5。这是由于翼型过失速升力系数是先降后增[27],迎角30°时升力系数大于失速前的最大升力系数;且螺旋桨具有其独特的旋转效应,科里奥利力的存在导致桨叶存在“失速延迟”现象[28]。叶素理论气动数据失真引起此处计算结果不准确。

图4 0.267R处的叶素压力云图Fig.4 Pressure contour of blade element at 0.267R
本文采用的计算机性能为:4核8线程3.4 GHz处理器,16 G内存。以半涵道模型计算耗时为例:动量源法为2.5 h,MRF方法为6 h,滑移网格方法为45 h。
尽管动量源法在数值上与滑移网格等方法存在一定误差,但涵道与半涵道耦合流场下的宏观特性变化规律与滑移网格相同,同时可以显著减小网格量,提高计算速度。为进一步比较各方法把握流场特征的能力,分析其流场结构,本节着重比较半涵道螺旋桨的流场与前两者的不同及特点。取各计算模型压力分布云图如图5所示。
由图5(a)、图5(b)可以看出,单独螺旋桨的压力分布有蝴蝶型高压区,这是桨尖涡系与桨叶高压区的叠加结果,而涵道的耦合作用使得桨尖涡系消失,桨盘前低压区显著增强和扩大,涵道内壁几乎全部处于低压环境下。
半涵道螺旋桨的流场兼具螺旋桨与涵道螺旋桨的特点。从宏观力(力矩)来说,半涵道性能更接近螺旋桨,流场中存在桨尖涡系,但由于与翼面的耦合作用,桨盘前低压区也显著扩大、增强,并影响了螺旋桨尾迹的发展方向。
由图5(c)、图5(d)可以看出,MRF方法计算结果有明显错误,其尾迹偏折方向与滑移网格方法、动量源方法的结果相反。MRF方法在计算中不使物面发生运动,而是通过改变流动的参考系,来模拟螺旋桨、涵道等圆周对称的模型流动。然而,半涵道螺旋桨实际上是一个圆周非对称的构型,桨叶与物面间存在非对称的相对运动,气流的旋转不能模拟非圆周对称的相对运动,所以MRF的计算结果不能作为“非定常流场的瞬态结果”。因此,在下文计算分析中,不再使用MRF方法计算非圆周对称的模型。
由图5(d)、图5(e)可以看出,动量源方法取得了与滑移网格方法相似的流场结构。由于动量源方法是将有限桨叶上的载荷按照流动规律分布在整个桨盘上,所以计算结果中没有体现桨尖涡系和桨盘前后相对集中的低压、高压区,压力分布更为缓和均匀。但是,动量源方法的高低压分布规律、尾迹发展规律均与滑移网格方法的时均结果一致,如桨盘前低压区沿物面向前延伸、桨盘后高压区沿物面向后延伸、桨盘后桨毂受低压区包裹、尾迹向下偏折等特征。因此,为节省计算资源,在下文机翼翼型优化计算中,将采用动量源方法进行计算。
1.3 半环形机翼模型
本文主要针对低速、垂直/短距起降状态的CW构型进行研究。为进一步验证本文研究对象下动量源法与滑移网格方法的计算可靠性,对本文使用的基准CW模型进行计算。使用1.2节中的螺旋桨,机翼弦长cwing=0.5 m,机翼展长lwing=1 m,基准翼型选择NACA4418,机翼呈半涵道形状,凹陷部分机翼环绕螺旋桨120°,螺旋桨布置于机翼0.5倍弦长处,其模型如图6所示。
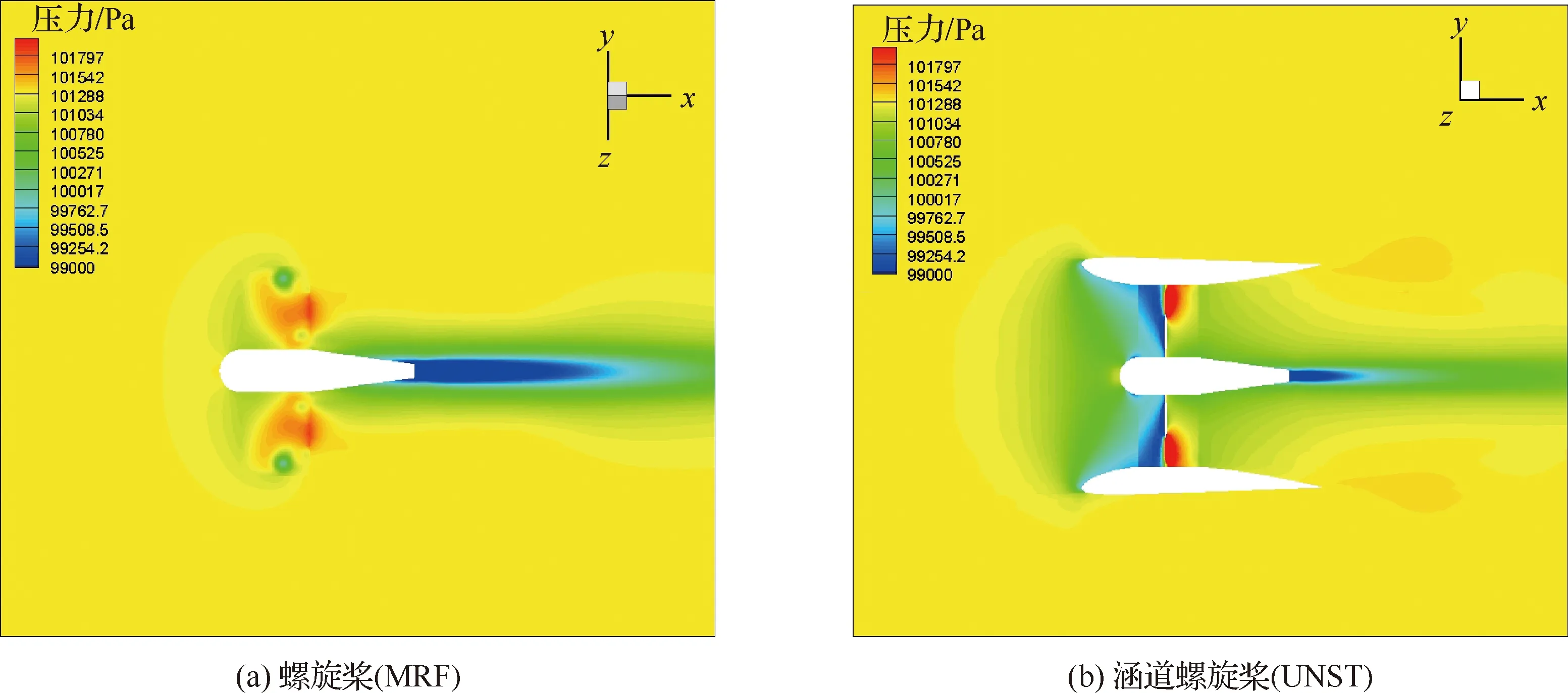

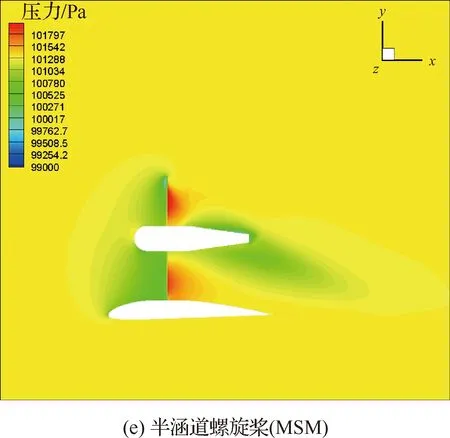
图5 涵道/半涵道螺旋桨压力云图Fig.5 Pressure contours of ducted/semi-ducted propeller

图6 CFD计算模型示意图Fig.6 Schematic of CFD computation model
计算方法分别采用动量源法和滑移网格非定常方法,其网格如图7所示。动量源方法结构化网格约为130万,滑移网格方法静止域结构化网格约为166.4万,旋转域非结构网格约为99万。计算状态同1.2节。
表3为动量源方法与滑移网格非定常方法的计算结果,滑移网格方法计算结果为时均结果。
桨盘特性的计算结果与1.2节规律一致,且机翼升力与阻力特性计算结果吻合良好。机翼对称面的压力分布如图8所示。
两种方法的机翼对称面流场结构相似,规律与1.2节半涵道相同。取机翼上表面的压力分布如图9所示。图中螺旋桨旋转方向为-x轴方向(左侧上行、右侧下行),动量源法与滑移网格非定常方法压力分布吻合良好。旋转效应使得翼面压力分布向着尾迹一侧偏移;半涵道边缘对其内部压力分布产生一定的分隔作用,产生明显的压力分布界限,这将在一定程度上保护翼型流场的二维特性,因此下文对翼型进行优化时,为节省计算资源,将采用二维CFD方法。

表3 动量源方法与滑移网格非定常方法计算结果Table 3 Computational results of MSM and UNST methods

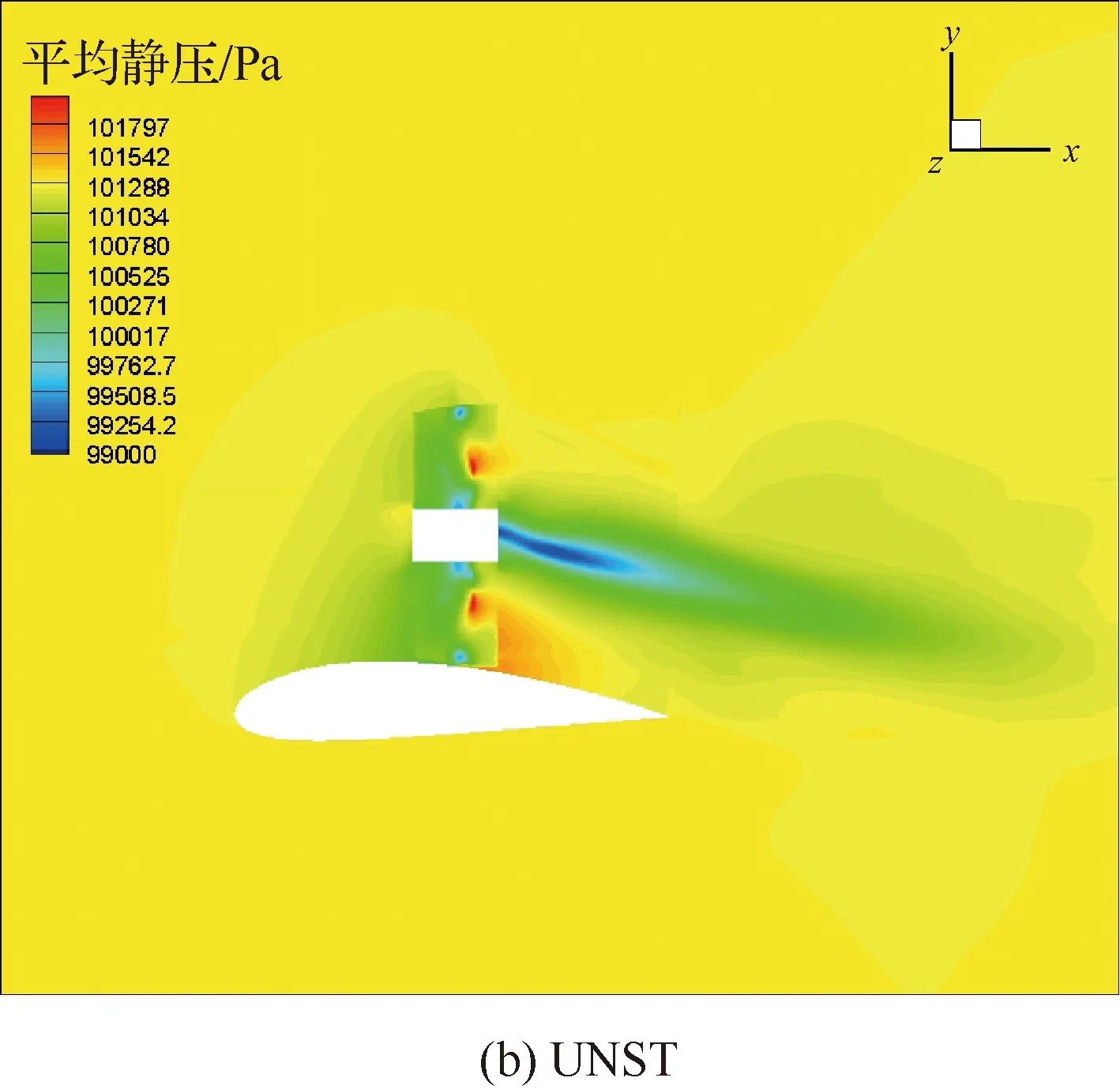
图8 机翼对称面的压力分布云图Fig.8 Pressure contours at wing symmetry plane
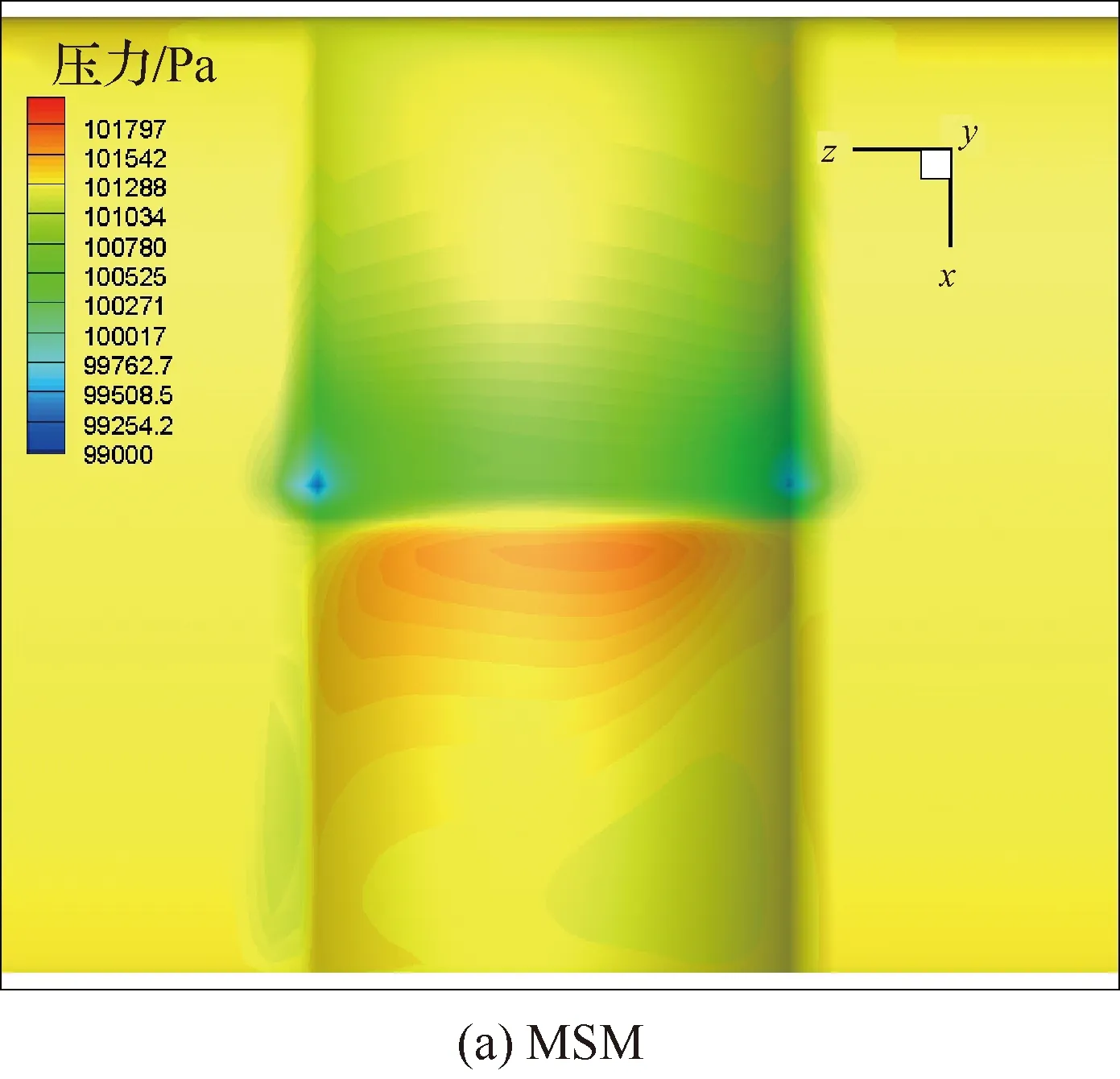
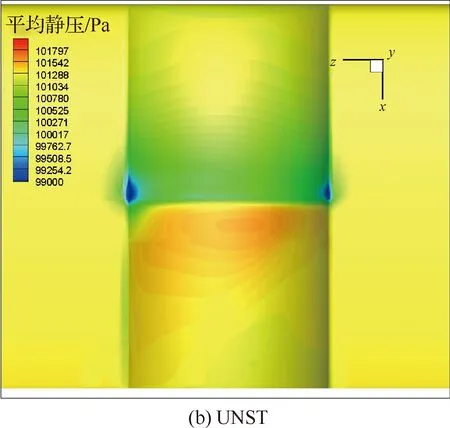
图9 机翼上表面的压力分布云图Fig.9 Pressure contours at upper wing surface
2 OTWP构型翼型优化
2.1 基准OTWP二维构型及其参数化
选取翼型弦长c=0.5 m,螺旋桨尺寸与计算状态与1.2节计算条件相同。为充分研究桨盘前后的翼面形状变化,将螺旋桨布置于机翼0.5倍弦长处,桨尖与翼面间隙控制在桨盘直径的1%以内[29-31]。基准翼型选择NACA4418,其构型如图10所示。
出于将来应用于三维的考虑,本文采用自由型面变形(Free Form Deformation,FFD)[32]方法对翼型和网格进行参数化及变形。
本文建立的翼型控制点如图11所示。图中方形控制点为可以控制翼型变形的控制点,而黑色控制点则是为了保证翼型周围网格连贯、光滑过渡的控制点,在变形过程中其坐标不变。移动控制点可任意改变翼型形状,如图12所示。由于不是为了进行翼型的微调修型,而是采用全局最优化方法得到一种适合于OTWP构型机翼的新翼型,网格变形方法必须能够适应较大幅度的变形,为检验网格变形能力,图12中变形最大幅度为0.3倍弦长c。

图10 OTWP二维构型Fig.10 OTWP 2D configuration
FFD方法对其网格变形示意图如图13所示。在图中所示剧烈变形下,变形后网格质量可以保持在0.45以上,正交性0.3以上。在使用过程中对变形范围进行限制,同时可用多轮优化来避免过大的网格变形。

图11 控制点与翼型Fig.11 Control points and airfoil
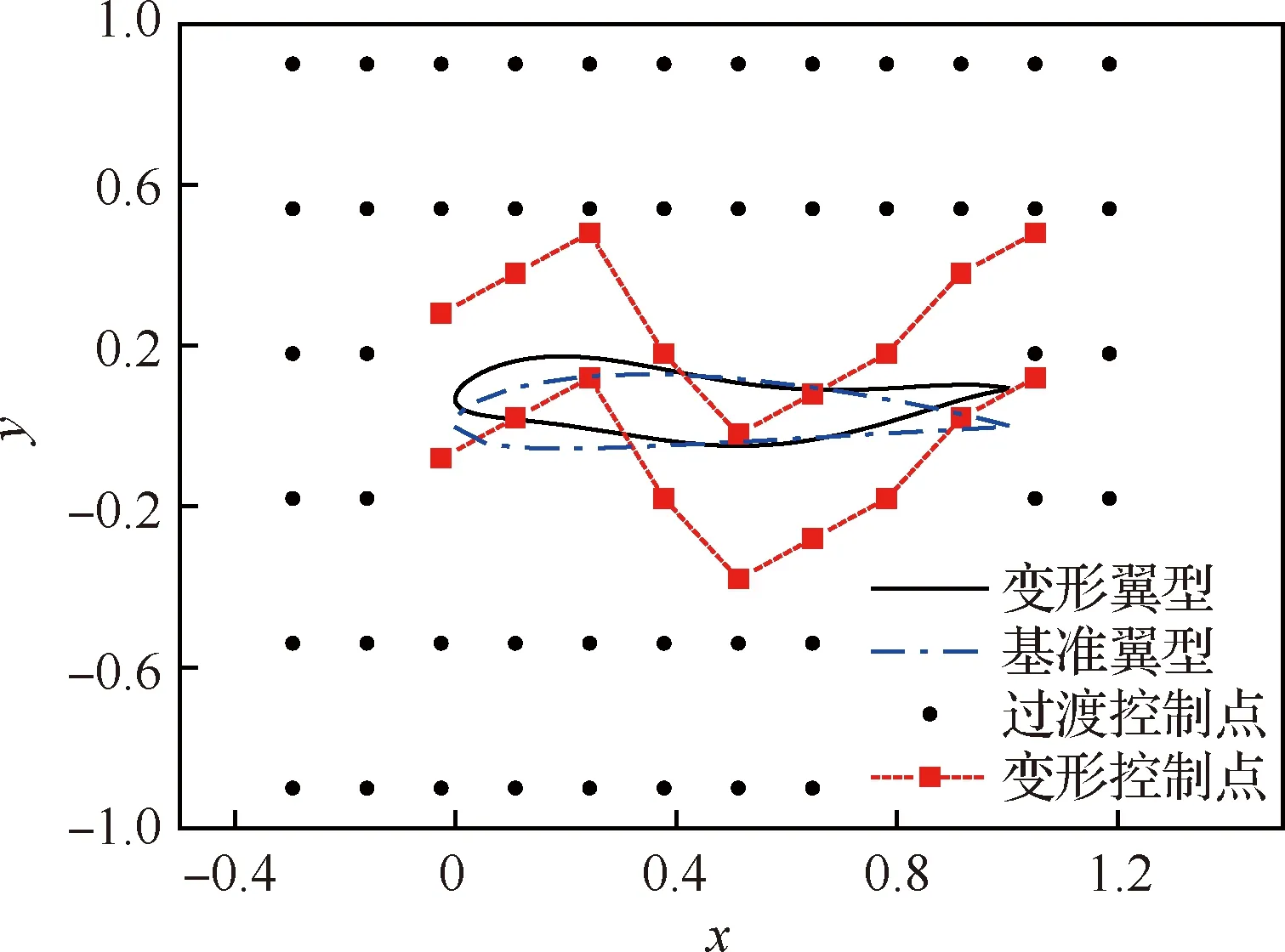
图12 翼型变形示例Fig.12 Airfoil deformation example
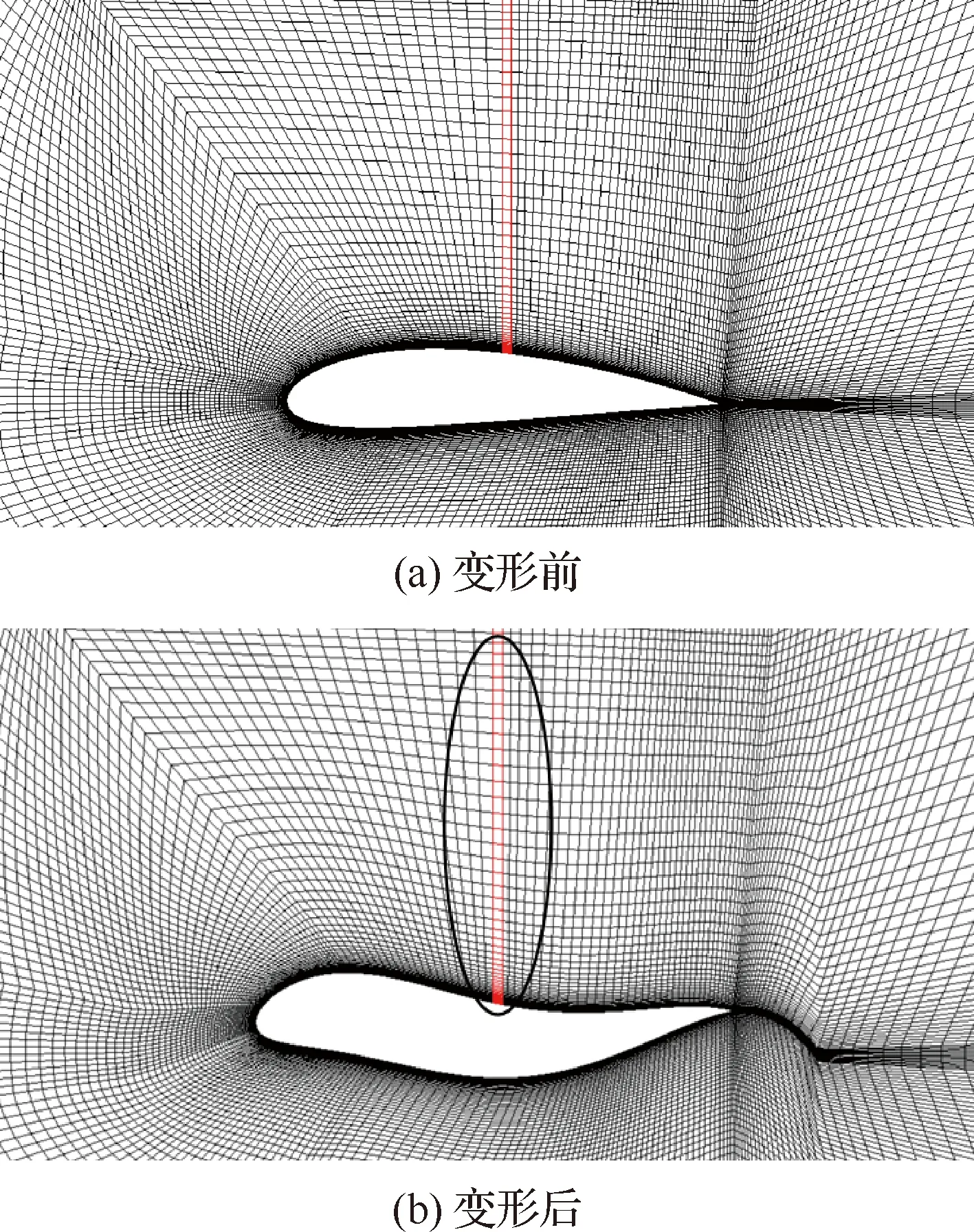
图13 网格变形示例Fig.13 Mesh deformation examples
图13中椭圆所框出的网格浅色部分为动量源搜索区域,搜索桨盘对应位置的网格进行动量源设置。在本文中,控制点不进行弦向移动,因此可以保证桨盘平面位置不变,且使动量源搜索区域保持直线。
2.2 优化方法
尽管由于三维泄流效应以及真实模型与二维简化模型的差异,二维与三维计算结果有较大差异,但其流场结构有一定相似性,且CW构型可以一定程度保护二维特性。为了尽可能降低计算代价,本文在优化中均使用二维CFD方法。二维结构化网格约为3.25万(如图13(a)所示),网格质量大于0.8,正交性大于0.4,其他条件同1.2节。桨盘使用动量源法进行模拟[20]。
为了控制变量,在优化中避免螺旋桨性能受翼型影响产生较大变化,二维动量源采用给定拉力分布的方式建立动量源项[21-23],且忽略旋向速度造成的影响。所用螺旋桨在优化工况下的拉力约为123.58 N,其拉力分布如图14所示。
本文应用遗传算法对OTWP构型翼型进行优化。遗传算法是一种全局优化算法,尽管本文应用了NACA4418作为初始翼型展开种群,但原始翼型仅表征一个局部最优点,在种群进化过程中,将会有部分个体落入其他局部最优点,最终进化得到各个局部最优点中相对更优的解,进而可以通过该全局最优化方法得到新的翼型。
为了避免翼型阻力发散(阻力增加将减小短距起降状态的净推力),将优化目标设为翼型升力L与阻力D的差值最大化(由于该构型下阻力可能出现负值和接近零的值,因此不能使用升阻比;同时,由于来流动压很小,力系数将是一个很大的值,此处不进行无量纲化)。优化参数为图11中18个变形控制点的纵坐标位移向量Y,在变形过程中,限制桨盘处的变形量Y0.5c在一个小量,以保持小的桨尖间隙、避免翼面与桨盘发生干涉。同时限制变形量以避免产生畸形网格,为了产生足够变形量,可进行两轮优化。
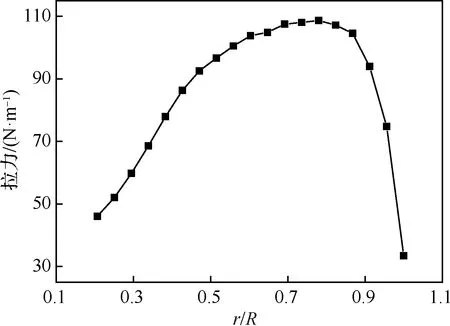
图14 螺旋桨拉力分布Fig.14 Propeller thrust distribution
优化设计模型为
maxL-D
式中:Ymax指控制点位移量的最大值,即纵坐标上下浮动不超过0.3c。
优化框架如图15所示。首先随机产生初始种群,将种群的控制点位移量读入FFD程序,程序判断若符合变形限制,则直接输出变形后的新网格,由CFD程序读入新网格进行计算,最后取出CFD计算结果进行适应度计算,随后产生下一子代;若变形超过限制,则不进行网格变形和CFD计算,直接给予惩罚性数值。

图15 优化框架Fig.15 Optimization framework
遗传算法子代规模为:5个种群,每个种群10个个体,交叉概率为0.8,变异概率为0.01,迁徙概率为0.2。控制点向量范围设为±0.3c。
2.3 优化结果
经过两轮优化,优化后的翼型及控制点示意图如图16所示。由于在低速状态下,桨盘抽吸和滑流作用主要体现在翼型上表面,因此本文着重研究翼上表面的变形情况。为了定量分析优化前后翼型变形的特征,对比前缘、0.4cwing、0.7cwing、0.9cwing这4处翼上表面的曲率变化情况,并参照涵道桨盘进口和出口的收缩扩张角参数,定义翼型参数如图17所示。图中d0c、d0.4c、d0.7c、d0.9c分别为前缘、0.4c、0.7c、0.9c处翼上表面的曲率半径,θin和θout分别为收缩角和扩张角。优化前后的各参数对比如表4所示。
优化后,翼型的前缘半径增大,一方面可以增大前缘吸力的作用面积,另一方面可以减小气流从下表面到上表面绕流的运动曲率,从而延缓分离。桨盘前翼表面曲率增大,因为较大曲率的附着流动可以增加Coanda效应的吸力。桨盘后翼面的变化较为剧烈,基准翼型从0.7c~0.9c的曲率相近而变化和缓,且0.9c曲率略大;而优化翼型桨盘后(0.7c)的曲率显著增大,但下游曲率(0.9c)显著减小,这与文献[14]的研究结果是相似的。桨盘出口附近的流动能量较高,因此较大的曲率有助于提高Coanda效应的吸力,而经过较高曲率引起的逆压梯度后,下游气流能量显著减小,更容易产生分离,为了保持附着流动必须减小翼面曲率。
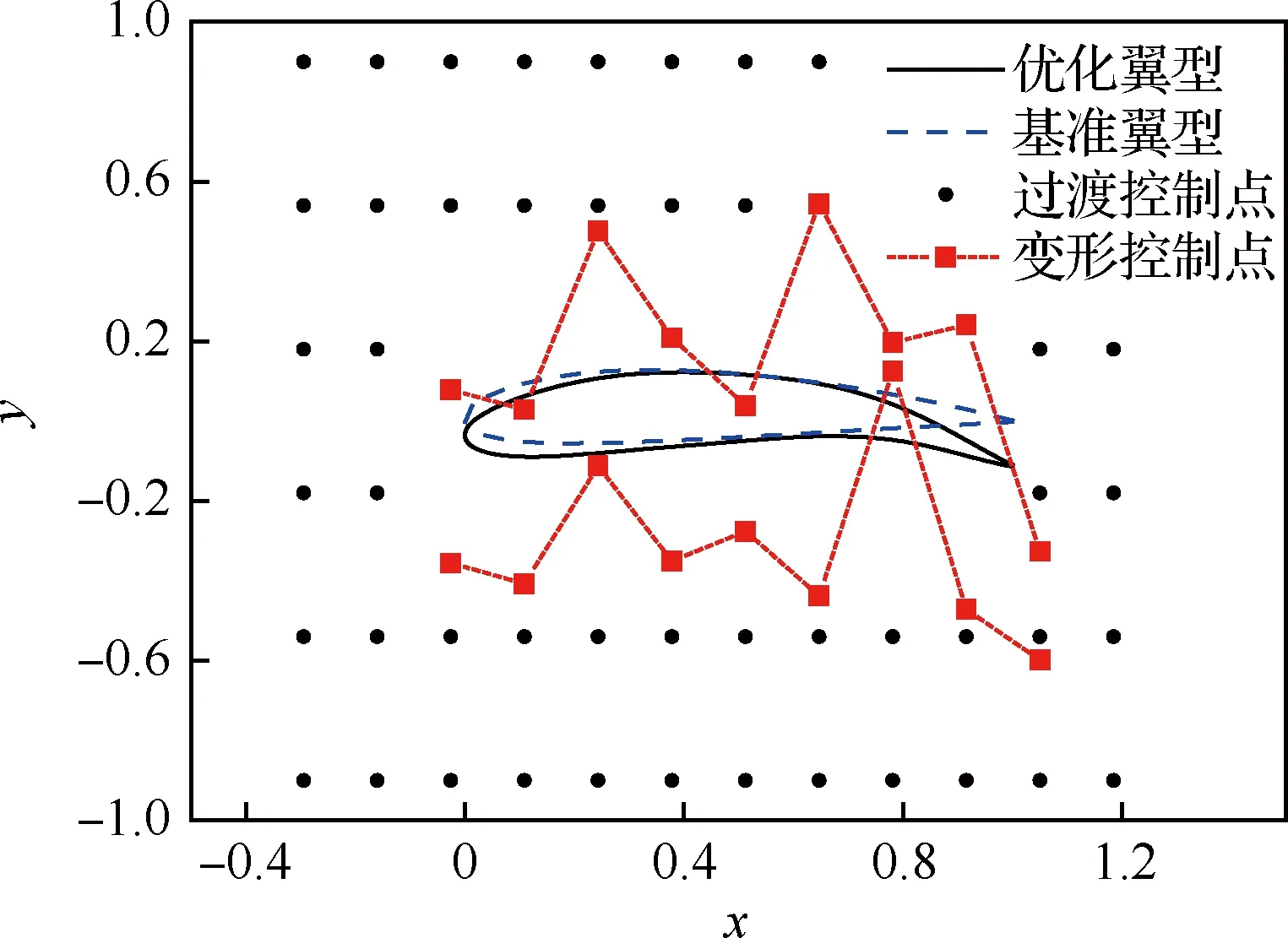
图16 优化翼型与控制点Fig.16 Optimal airfoil and control points

图17 翼型参数定义Fig.17 Airfoil parameters definition

表4 基准翼型与优化翼型参数对比Table 4 Comparison of baseline and optimal airfoil parameters
此外,收缩角与扩张角均显著增大。收缩角增大进一步减小了气流翻越前缘时的翻越角度,减缓分离,并增加了翼面在吸力方向上的投影面积,进而减小阻力;扩张角增加可以增大气流向下的偏折角度,增加升力(阻力也将增加)。
在优化计算状态下,优化前后翼型的性能如表5所示,其中力矩参考点为0.25c处。在优化计算条件下,优化后翼型的升力提高了77.73%,但阻力由负值变为正值,一定程度上减小了净推力。
优化前后的翼型压力云图、速度云图、压力系数Cp曲线如图18~图20所示。

表5 基准翼型与优化翼型性能(2D)Table 5 Performance of baseline and optimal airfoil (2D)
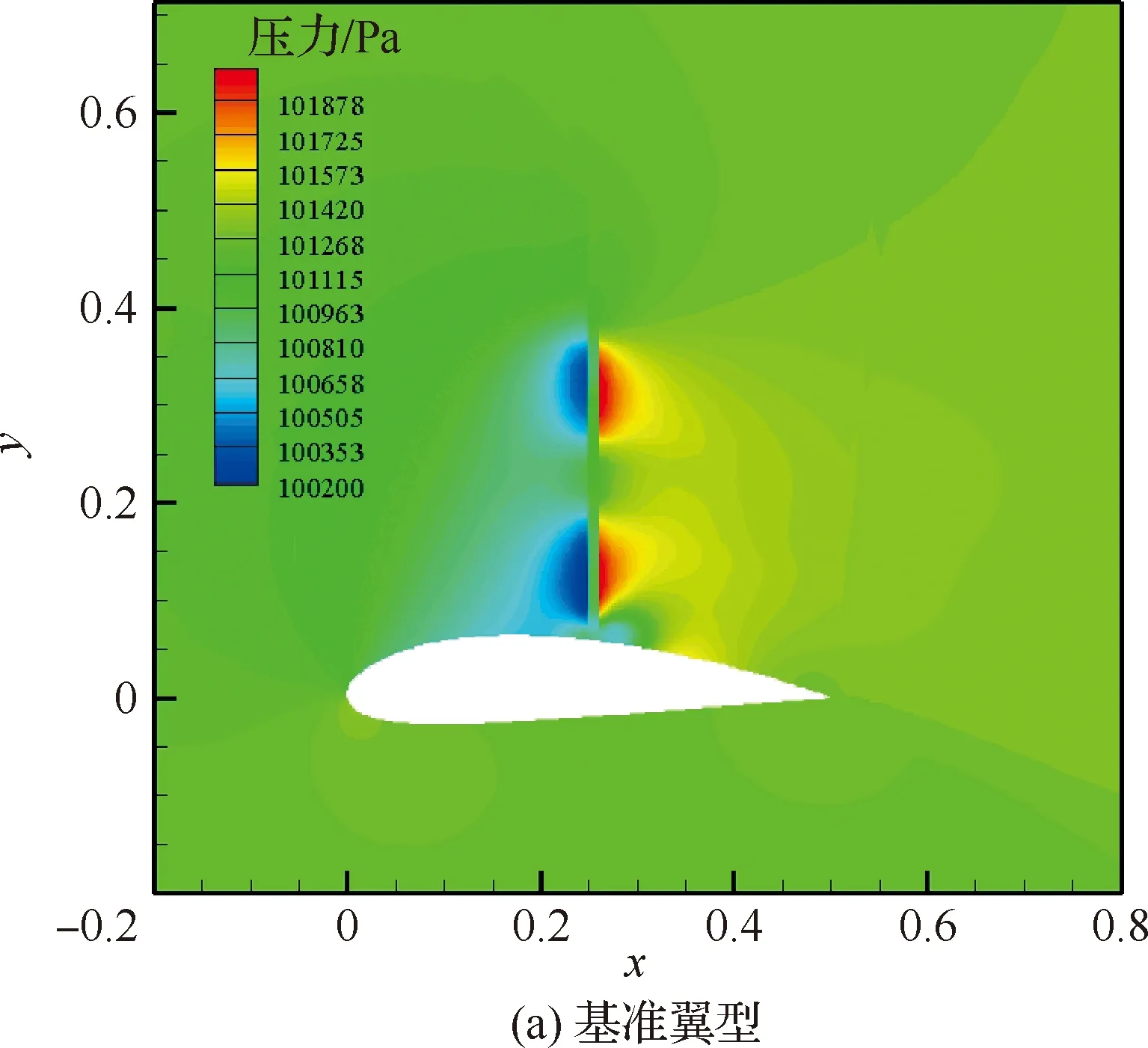

图18 优化状态下的压力云图Fig.18 Pressure contours in optimization condition
由图18可以看出优化后翼型桨盘前低压区显著扩大,低压区受物面的牵引现象更加明显;同时,优化前桨盘后存在高压区受物面牵引的现象,物面出现一段高压区,而优化后该现象消失,较高翼面曲率导致的Coanda效应产生了较强的吸力,整个桨盘后翼面全部呈低压。这一点在图20中有鲜明体现。
由图19可以看出,桨盘后翼面曲率的增加显著增加了物面附近的流速,Coanda效应得到了较好的利用。由于桨盘与翼面间保留了一定间隙,间隙附近存在强烈的桨盘吸力、速度剪切和逆压梯度(桨盘前为低压,桨盘后为高压),因此基准翼型的间隙位置附近产生了明显的桨盘诱导分离现象,并使得该处吸力减小(图18(a)及图20可以反映该现象),尽管分离在桨盘后能够再附着,但其限制了物面吸力峰值的发展。优化翼型通过将桨盘后物面压力降低为低压,减小逆压梯度,显著减弱了桨盘诱导分离,使吸力峰值增加。
翼型后部的吸力增加了低头力矩。由于桨盘后翼面法线朝向后上方,此处吸力的增加也显著增加了翼型阻力(见表5),因此优化翼型的后缘扩张角没有进一步增加。

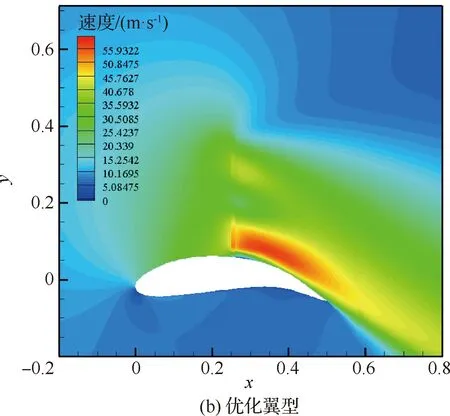
图19 优化状态下的速度云图Fig.19 Velocity contours in optimization condition

图20 优化状态下的压力系数Fig.20 Pressure coefficients in optimization condition
3 三维CW优化构型
为了检验二维条件下优化结果在三维构型上的性能,本节采用动量源法对优化前后三维机翼进行计算分析。
3.1 CW构型气动特性
计算模型和方法与1.3节保持一致,优化CW构型仅将其翼型更换为优化翼型。优化前后三维CW构型气动特性如表6所示,其中机翼力矩参考点位于0.25cwing处。

表6 优化前后CW构型气动特性Table 6 Aerodynamic performance of baseline and optimal CW model
由计算结果可以看出,受三维泄流效应及几何模型的差异影响,三维机翼的升力、阻力较二维优化状态结果(表5)显著降低,变化幅度也大幅下降(优化翼型提高三维机翼升力约22.51%),但其变化趋势也与二维优化结果一致。三维机翼的阻力全部保持了负阻力特性,优化后机翼负阻力(绝对值)减小,低头力矩增大,螺旋桨效率略微降低。
螺旋桨效率降低的原因,可以理解为能量转化的结果。将机翼与螺旋桨作为一个整体来看,优化后的构型合力提高了约1%,同时,螺旋桨的效率也下降了约1%,这其中存在着由螺旋桨拉力到机翼升力的能量转化,但系统的吸收功率仅提高了不到0.3%,系统总的效率有少许提高。
3.2 优化构型流场特性
优化后机翼对称面的压力分布云图(MSM)如图21所示。图22为机翼对称面的压力系数曲线。
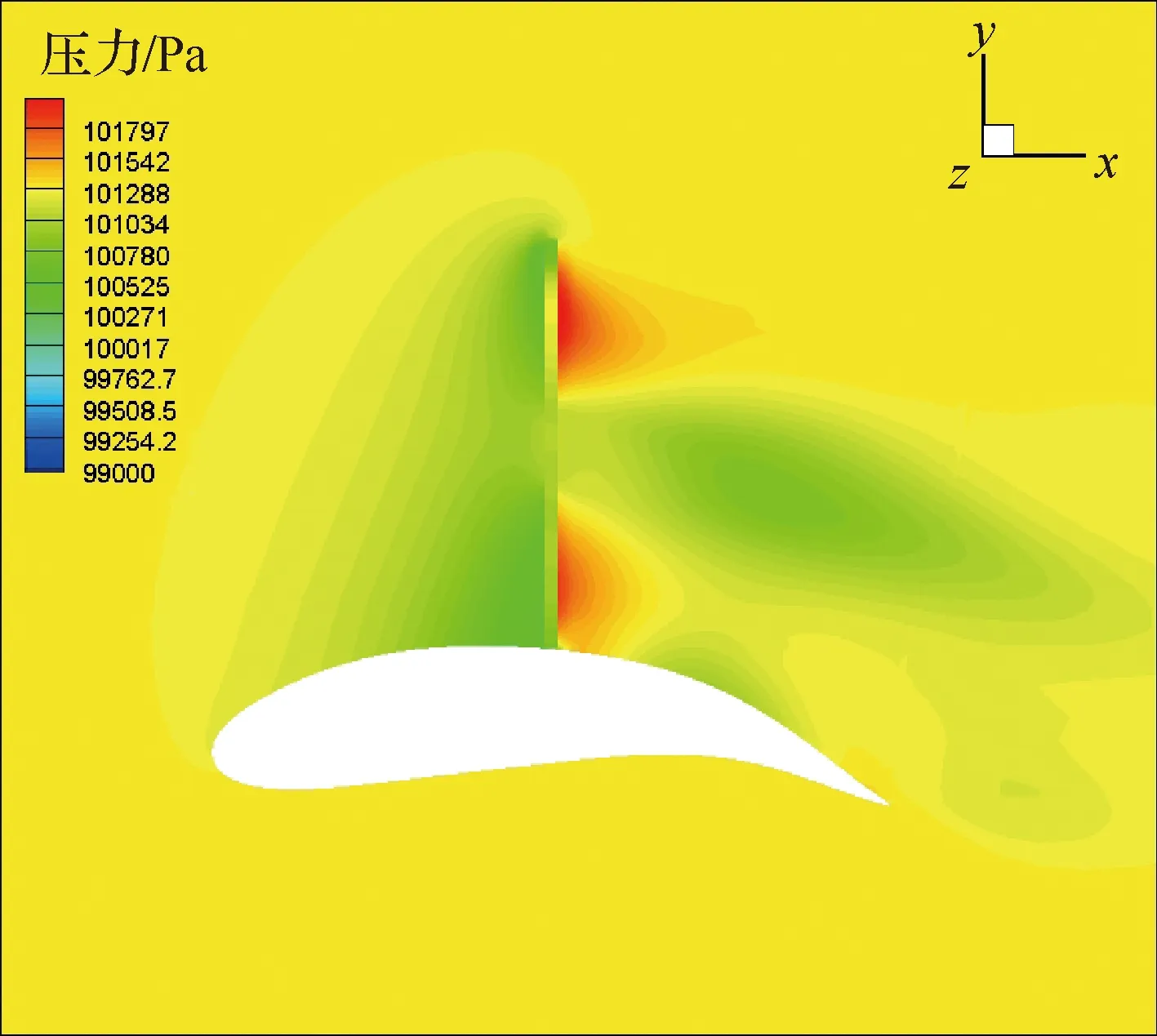
图21 优化后机翼对称面压力云图Fig.21 Pressure contours of optimal airfoil at wing symmetry plane
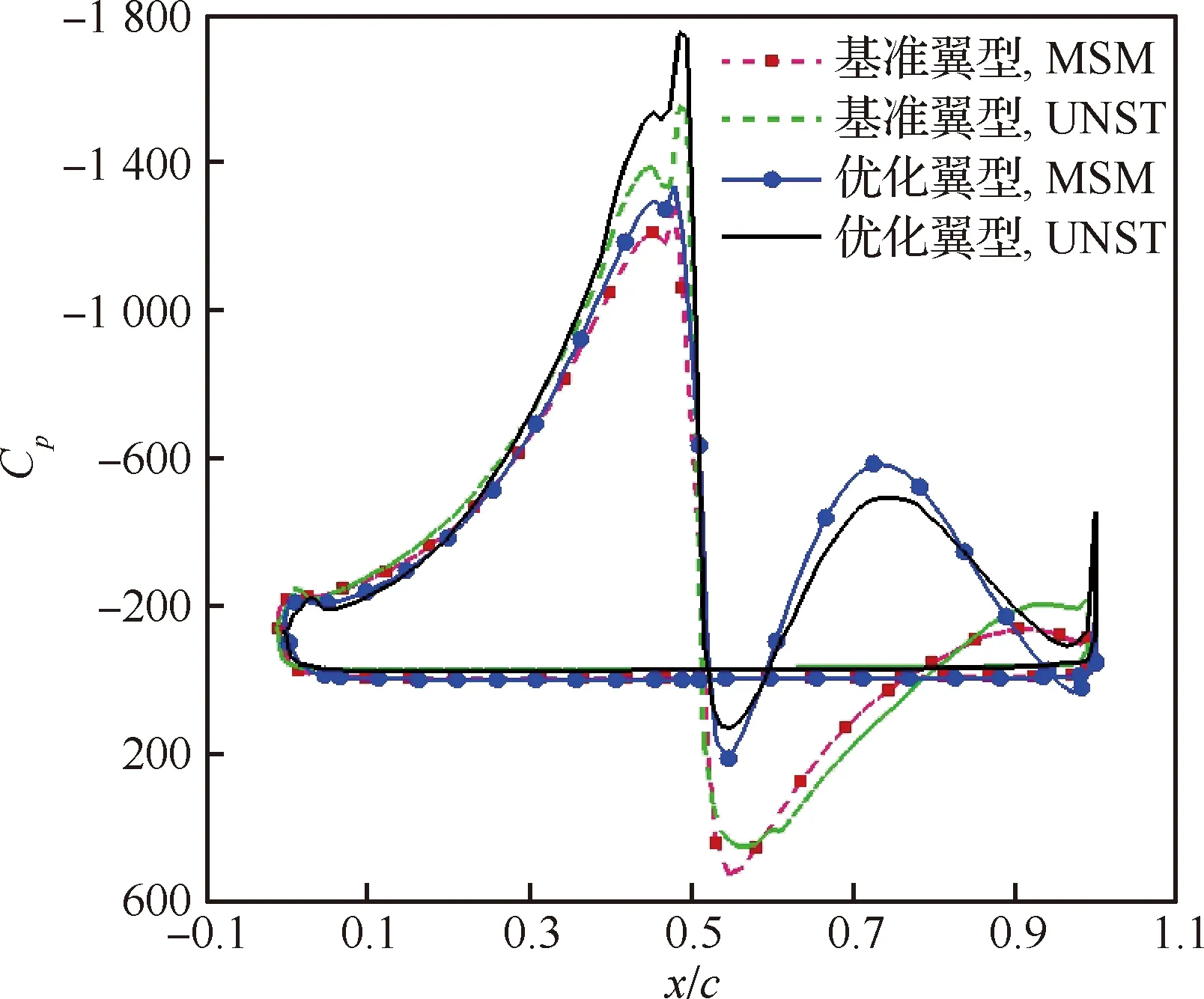
图22 机翼对称面处的压力系数曲线Fig.22 Pressure coefficient curves at wing symmetry plane
由于三维泄流效应减小了桨盘后Coanda效应吸力,0.7c处吸力峰值的减弱(图22)在减小升力分量的同时也减小了阻力分量,因此优化构型机翼阻力可以保持负阻力。
三维计算结果显示,优化翼型的桨盘前吸力峰值增大,而0.7c处产生二次吸力峰值,与二维计算结果趋势一致。图21(与图8(a)对比)所反映的流场结构以及图22的压力系数曲线趋势与二维计算结果吻合较好,仅在数值高度与变化幅度上有所差别。观察发现,二维优化所得优势在三维能够得到有效的继承。
对比分析上翼面非对称流场结构,机翼上翼面压力分布云图(MSM)如图23所示。图中螺旋桨旋转方向为-x轴方向。与基准翼型(图9(a))相比,受旋转速度影响,桨盘后压力(基准翼型为高压区,优化翼型为低压区)向旋转速度一侧进行偏移发展。由于三维效应导致0.7c处低压减弱,优化翼型没有将桨盘后全部变为低压,而是在桨盘后附近出现小范围高压,而后受0.7c处Coanda效应的影响发展为低压区。压力分布在半涵道边缘界限较为明显,半涵道一定程度上保护了二维特性。
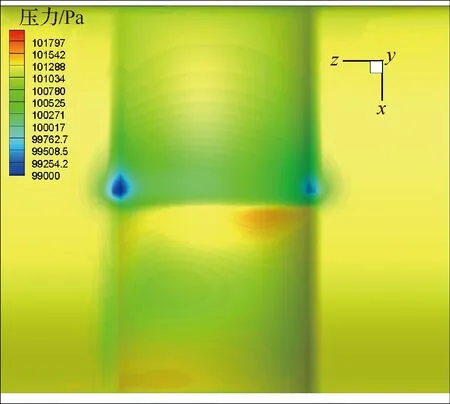
图23 优化后机翼上表面的压力分布云图(MSM)Fig.23 Pressure contours of optimal airfoil at upper wing surface(MSM)
由于模型的非对称性,桨盘载荷也将呈非对称分布。取桨盘后(0.52cwing)的桨盘压力分布如图24所示(动量源方法)。图中视线方向沿-x轴,螺旋桨旋转方向为顺时针。桨盘后压力在上行桨叶一侧减小,而在下行桨叶一侧增大。
优化前后机翼对螺旋桨压力分布的影响较为微弱,压力分布变化不明显,因而优化前后的螺旋桨性能也无明显变化(表6)。
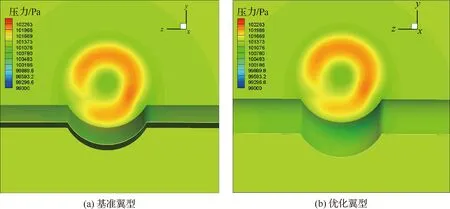
图24 0.52cwing处的压力分布云图Fig.24 Pressure contours at 0.52cwing
4 结 论
1)针对OTWP构型对比了动量源法、MRF准定常方法、滑移网格非定常方法的计算结果。结果表明MRF准定常方法虽然可以比非定常方法节省计算时间,但不能对OTWP构型等非圆周对称的模型进行准确计算;动量源方法与滑移网格方法对OTWP构型的计算压力分布与流场结构较为吻合,且能够节省计算资源,计算效率和准确性可以满足设计计算的要求;由于CW构型中半涵道边缘对二维特性有一定保护作用,因此二维计算方法的气动优势可以在三维构型中得到有效继承。
2)OTWP构型中,桨盘前低压区受物面牵引沿上翼面向前延伸,吸力峰值位于桨盘前;桨盘后高压区也有沿翼面向后延伸的趋势,翼面附近流速显著加大,可以通过加大桨盘后翼型上表面曲率(距离桨盘越远,翼表面曲率应当越小)来增加Coanda效应吸力,产生二次吸力峰值。
3)在本文计算条件下,对CW构型的翼型优化使得其诱导升力提高22.51%(二维计算条件下提高77.73%),优化翼型显著改善了翼型压力分布,提高了桨盘前主吸力峰值,并利用Coanda效应将桨盘后的高压区变为低压区,产生二次吸力峰值。优化前后机翼均保持了负阻力特性,CW构型在垂直/短距起降过程中可以起到较为显著的增升减阻的作用,具有一定的工程应用潜力。

